2D Vector in C++

In C++, 2D vectors, or 'vectors of vectors,' act like dynamic matrices. They efficiently store elements in contiguous spaces, allowing variable sizes and easy access. Essential for creating flexible structures, 2D vectors differ from single-dimensional ones in their ability to dynamically resize and hold multiple vectors.

Including the Vector Header File

The C++ Standard Template Library includes vectors. We must include the vector header file in our program to use vectors.

Instead of including numerous kinds of Standard Template Libraries (STL) one by one, we can include all of them by:

Initializing a 2D Vector in C++

Let's say you want to initialize a 2D vector, m * n, with the initial value to be 0.

We could do this:

• Declaration:

The above code produces a 2D vector that is empty. Before using it, we must set the vector size and provide space for its components. The fill function constructor, the resize() and push_back() methods, and other techniques can all be used to build a two-dimensional vector.

• Making use of Fill Constructor For initializing a two-dimensional vector, it is advised to utilize a fill function constructor.  The fill function constructor creates a vector with the required number of elements, and the value specified is filled into it.

Two stages can be used to break down the initialization described above: Create an int vector and initialize it with a default value before using it to create the two-dimensional vector. As an illustration, consider the following:

• Use of the resize() method:

Here are two implementations that utilize an overloaded version of the resize() function that accepts two arguments: the size of the container and the object to be copied:

To resize a vector to the desired size, use the resize() function. It can be used to set a default value for a two-dimensional vector, as demonstrated below:

Remember that the preceding code may run worse when M and N are large due to the push_back() function's propensity to reallocate memory frequently. Therefore, push_back() should only be utilized when vector dimensions are unknown in advance.

• Making use of Initializer Lists Finally, as illustrated below, we can initialize a two-dimensional vector with an assigned default value using initializer lists. Please take note that only C++11 and higher support this.

Specifying the Size for 2D Vector Initialization

The 2D vector can be initialized with a user-defined size as well. It is similar to using the new operator or malloc() to create a 2D dynamic array. Consequently, if we want to establish a 2D vector to rows n and columns m, we must start a 2D vector of size n with elements from a 1D vector of size m. We may accomplish that by following the steps below. The 2D array's values are default set to 0.

As previously stated, A 2D vector is a vector of a 1D vector.

Let's think about the upper use case precisely like a 1D vector.

The outer vector is, therefore, of size n(number of rows).

Iterators for 2D Vectors

• Use range-based for loops to iterate through a vector in C++.

In C++11, range-based for loops were first made available. A more understandable way of looping over a container is helpful. Let's examine how we can iterate over an array of integers using this range-based for loops and print each entry as we go.

Output:

Here, we iterated over all the vector's components, using the auto type to choose each. The advantage of this strategy is that the type of the vector's elements need not be specified. Additionally, we may perform various operations with each element in addition to printing them.

• Utilize indexing to iterate over a vector in C++. We iterated through each element in the vector in the preceding example. However, we were unaware of the index positions of the components during iteration. Therefore, we can use the standard for loop to iterate through all of a vector's elements by indexing. For instance, Iterate over a vector in C++ using indexing.

In the previous example, we iterated over all items in vector. But during iteration, we were not aware of the index positions of the elements. So, if we want to iterate over all vector elements through indexing, we can use the normal for loop. For example,

Output:

• C++: Iterate over a vector using Iterators

Syntax:

For each unique STL data structure, C++ offers iterators as an alternative to utilizing indices to navigate a 2D vector.

Output:

The iterators are useful when we employ specific operations that call for a positional argument. The top two functions that return iterator values are:

• v.begin() - This function returns an iterator that goes to the first vector in a 2-D vector.
• v.end() - returns an iterator that iterates across the 2-D vector until its end.
• C++: Iterate over a vector in a single line We can loop over every element of a vector in a single line by using the STL Algorithm for_each(start, end, callback). It will take three arguments: an Iterator pointing to the start of a range, also known as a start iterator, an iterator pointing to the end of a range, known as an end iterator, and a callback function discussed below.

Callback Function: A function that must be applied to each element in the range, starting at the beginning and ending at the end. Between start and end iterators, all the elements are iterated over for_each(), which applies the specified callback to each element. We can supply the for_each method with iterators pointing to the beginning and end of the vector. It goes through every element of the vector and applies the lambda function supplied to each one.

Adding Elements to a 2-D Vector

The C++ STL's push_back() method can be used to insert elements into a vector.

The insertion operation in a vector of vectors is shown in the example below. The push_back() function is used in the code to construct a 2D vector displayed alongside the matrix.

Time complexity is O(1).

Methods used to remove elements from vector are:

• vector_name.push_back(value)
• insert()

Where value refers to the element added to the vector's back.

Example 1:

This function pushes vector v2 into a vector of vectors v1. Therefore v1 becomes { {3, 5, 6, 7} }.

Output:

Since it is a vector of vectors, it would only make sense to push full vectors into our container. Therefore, the"push_back()" function requires a vector as an input.

Removing Elements From 2D Vectors in C++

Methods used to remove elements from vector are:

• vector::pop back() The method vector::pop back() removes elements from a vector. It eliminates the removed element and shrinks the container by one.

Syntax:

Exceptions and Errors:

1. No-Throw Guarantee: The container remains unchanged if an exception is thrown.
2. If a vector is empty, it behaves undefinably.

Does pop_back() eliminate values in addition to elements? The last element is eliminated when this method is called. The object's destructor is invoked, and the vector's length is reduced by 1.

Time Complexity: O(1) or (Amortized constant)

• vector::pop_front() There is no inbuilt function, pop_front(), for vectors, but it can be implemented on our own. We have to remove the first element, and since the rest of the elements needs to be shifted by one index to the left, the time complexity is linear. Time Complexity: O(N) Syntax:

Complete example:

Output

• vector::erase(): Removes either a single element or a range of elements.

Syntax:

Time Complexity: O(N) - worst case

An example of erase method is:

Output

Traversing the Entire Matrix Created Using a 2D Vector

There are two ways to move about in a matrix. Row-wise traversal goes over each row one at a time, starting with the first row, moving on to the second, and so on till the last row. From index 0 to the last index, elements from the row are returned.

Elements are traversed sequentially from the first to the last column using a column-wise traversal method.

M is a 2D matrix. Columns are represented by index j, while rows are represented by index i.

• For row-wise traversal, start from

• For column-wise traversal, start from

The order of indexes remains the same in the 2D array M[i][j]- i for rows and j for columns.

Examples

Input −

Output −

Example

If we run the above code, it will generate the following Output:

• Traversing diagonally: Given a 2D matrix, print all elements of the given matrix in a diagonal order. For example, consider the following 5 X 4 input matrix.

Example:

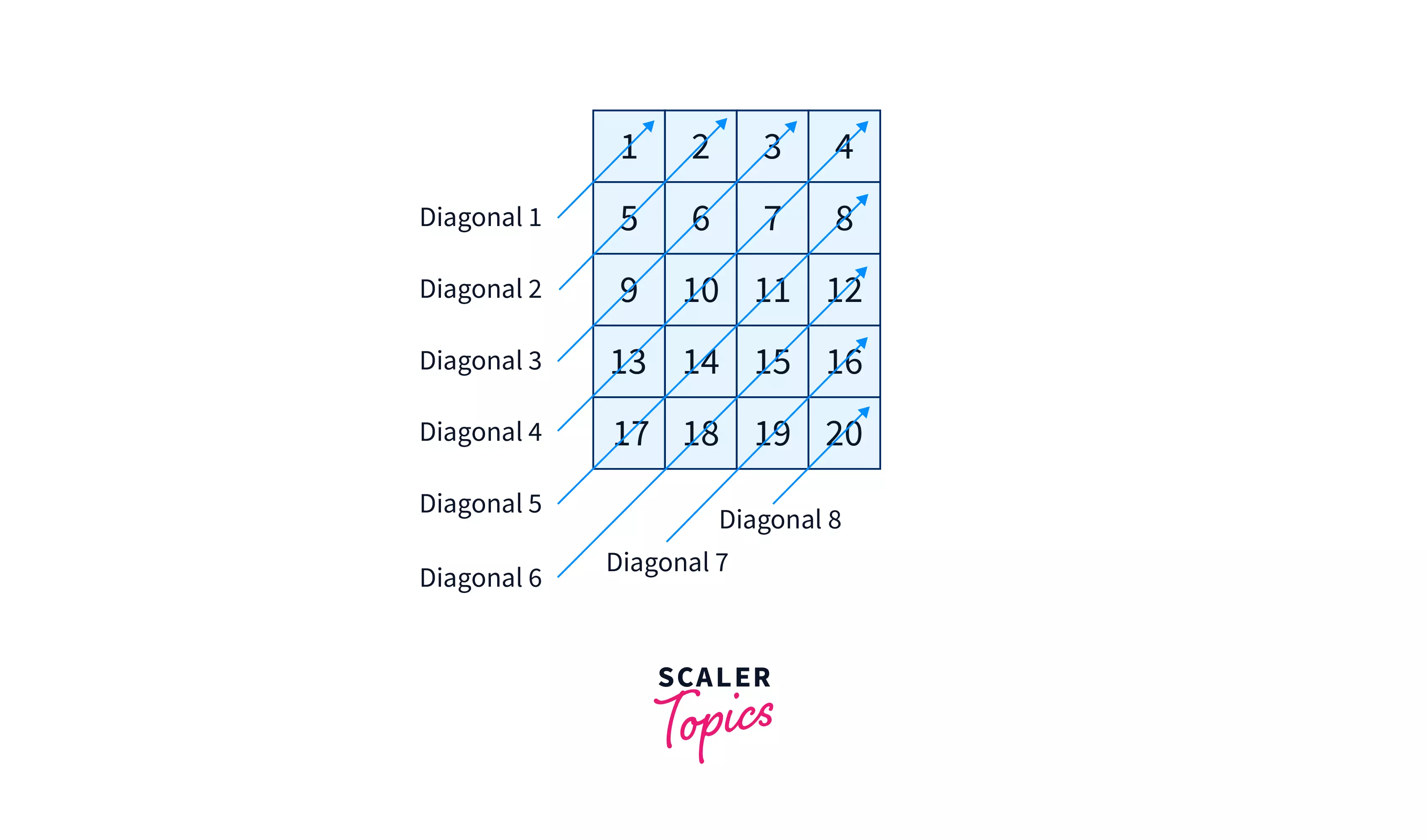
Diagonal printing of the above matrix is:

Implementation:

Input:

Output:

See Also:

• Auto in C++.