Activity Selection Problem

Example of Activity Selection Problem

Example Explanation

Suppose we are given the following 7 activities:

Let us create 2 different arrays for start and finish time and sort them by finish time for better understanding:

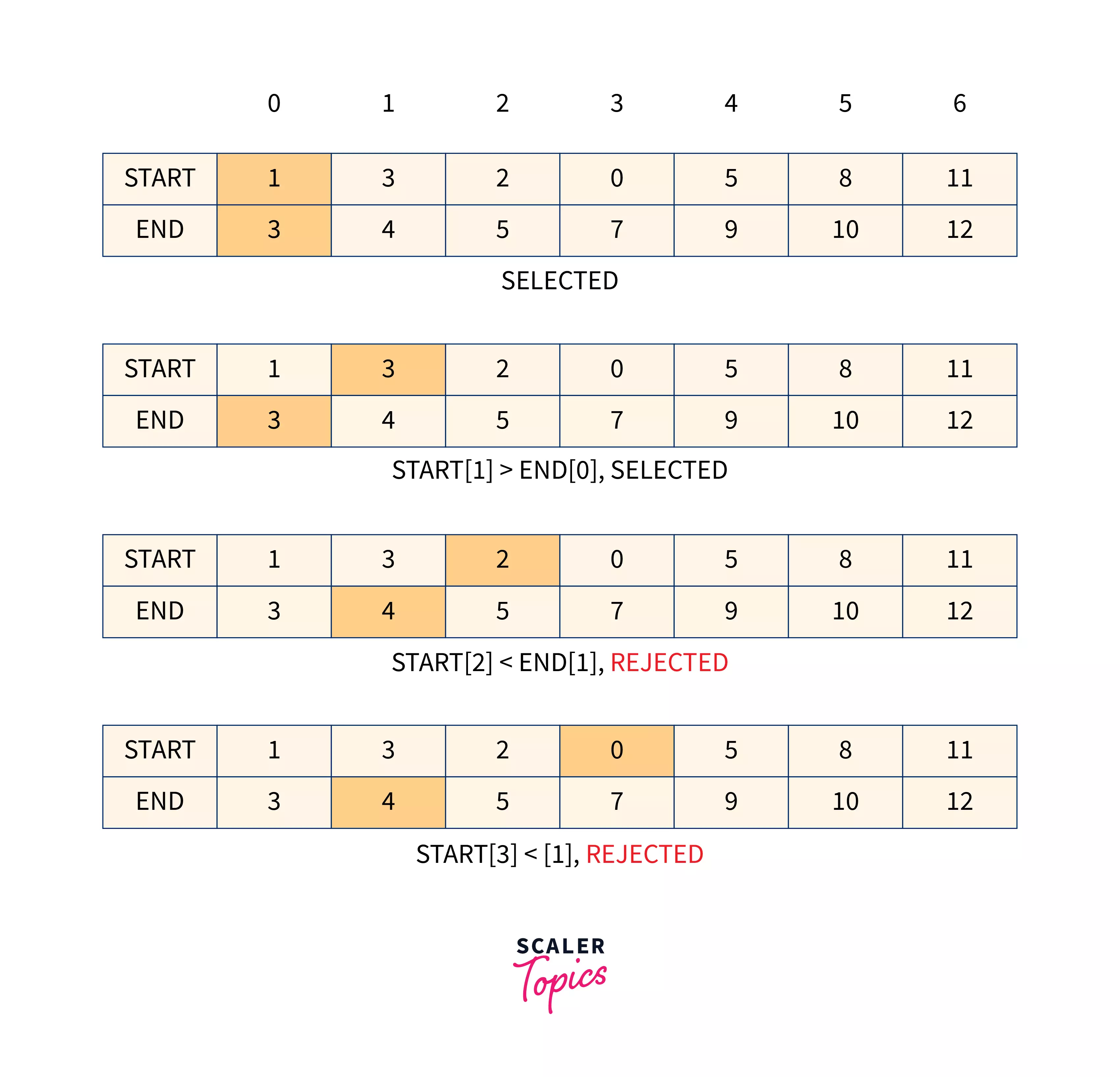
Since these activities are already sorted by their finish time, firstly the activity0 gets selected. As the start time of activity1 is equal to the finish time of activity0, it will also get selected. activity2 and activity3 are having smaller start times as compared to the finish time of activity1, so both these activities will get rejected.

Similarly activity4 and activity6 are also selected, whereas activity5 will be rejected. Therefore at the end of an iteration, activities at index 0, 1, 4, and 6 will be performed, while others get rejected.

Constraints of Activity Selection Problem

$1 ≤ N ≤ 2*10^{5}$

$1 ≤ arr[i] ≤ 10^{9}$

Approach 1: Greedy algorithm

• Intuition: This method uses the greedy approach and as the name suggests greedy means that at every step we have to make a choice that looks best at the moment and can provide us with an optimal solution for that problem.

  Since we have to maximize the number of performed activities, so we will be choosing the activity that will finish first as that will leave us with the maximum time to process the remaining activities. This greedy intuition enables us to make choices and provide us with an optimal solution and also helps us to get started with the solution. Therefore, our first task is to sort the activities based on their finish time.

  If we try to solve this problem by sorting the activities based on start time then there might be a case where the activity with the least start time takes maximum duration to complete thus preventing us from maximizing the number of activities.

• Algorithm:

  1. Sort all activities based on their finish time.
  2. Choosing the first activity from the sorted list.
  3. Select the next activity from the sorted list only if its start time is greater than or equal to the finish time of the previously selected activity.
  4. Repeat Step 3 for all the remaining activities in the sorted list.

• Implementation

C++ Program to solve Activity Selection Problem using Greedy Algorithm:

Output:

Java Program to solve Activity Selection Problem using Greedy Algorithm:

Output

Python Program to solve Activity Selection Problem using Greedy Algorithm:

Output

• Complexity Analysis:

  Case 1: When the provided list of activities is already sorted by finish time, then no need for sorting it again. Therefore, Time Complexity in such a case will be O(n).

  Case 1: When the provided list of activities is not sorted, then we will have to either write a sort() function from scratch or we can use the in-built Standard Template Library function. Therefore, Time Complexity, in this case, will be O(nlogn).

  Space Complexity: O(1), Since no Auxillary space is required.

Approach 2: Count the maximum number of non-conflicting activities

• Intuition This approach involves the use of dynamic programming, as this problem is a variation of Longest Increasing Subsequence (LCS). The intuition is to sort the given array of activities named arr by start time, after which we can create an array named dp, such that dp[i] stores the count of maximum activities that can be performed without conflict.

• Algorithm The recursive way of completing the dp[i] after every i'th activity is:

Let us take an example where sorted -

For the above example dp[] would be:

• Implementation

C++ Program to Count the maximum number of non-conflicting activities using Dynamic Programming

Output

Java Program to Count the maximum number of non-conflicting activities using Dynamic Programming

Output

Python Program to Count the maximum number of non-conflicting activities using Dynamic Programming

Output:

• Complexity Analysis

  Since we are using nested for-loops to traverse the list of n activities arr, Time Complexity :$O(n^{2})$

  While we are also using an array named dp to store the maximum number of non-conflicting activities, Therefore the Space Complexity approach for this approach is: $O(n)$

Approach 3: Print the maximum number of non-conflicting activities

• Intuition The approach for this section is the same as the previous one, but the difference here is that instead of printing the number of non-conflicting activities we have to print all these activities. Therefore, instead of doing dp[i]++, we will be adding arr[i] to dp[i] for every i'th activity.

• Implementation

C++ Program to Print the maximum number of non-conflicting activities using Dynamic Programming

Output:

Java Program to Print the maximum number of non-conflicting activities using Dynamic Programming

Output:

Python Program to Print the maximum number of non-conflicting activities using Dynamic Programming

Output

• Complexity Analysis

  Since we are using nested for-loops to traverse the list of n activities arr,

Therefore the Time Complexity approach for this approach is: $O(n^{2})$

While we are also using a matrix named dp to store the maximum number of non-conflicting activities,

Therefore the Space Complexity approach for this approach is: $O(n^{2})$