Application of Chi Square Test

The application of chi square test plays a pivotal role in statistical analysis, providing insights into the relationship between categorical variables in diverse fields.

What is Chi Square Test?

The application of chi square test is a cornerstone in statistical analysis, used to assess whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories. It's particularly useful in situations where data can be categorized, making it a staple in the fields of research, psychology, health sciences, and social sciences.

Formula

The formula for the chi-square statistic ($\chi^2$) is a key element in its application, providing a quantifiable measure of the discrepancy between observed and expected data. It is given by:

$\chi^2 = \sum \frac{(O - E)^2}{E}$

In this formula

• $\chi^2$ represents the Chi-Square statistic.
• O stands for the observed frequency.
• E represents the expected frequency.

Properties

Understanding the properties is crucial for the effective application of chi-square test:

• Non-negativity: The chi-square value is always non-negative since it is the sum of squared quantities.
• Sensitivity to sample size: The test's significance can be influenced by the size of the sample, with larger samples potentially leading to smaller p-values.
• Distribution: Under the null hypothesis, the chi-square statistic follows a chi-square distribution, with degrees of freedom dependent on the number of categories minus one.
• Applicability: It is most suitable for nominal data and ordinal data with a significant number of categories, ensuring the theoretical basis of the chi-square distribution is maintained.

Examples

The application of chi square test can be illustrated through various examples:

• Marketing Research: A company may use the test to determine if customer preferences for product features are independent of age groups.
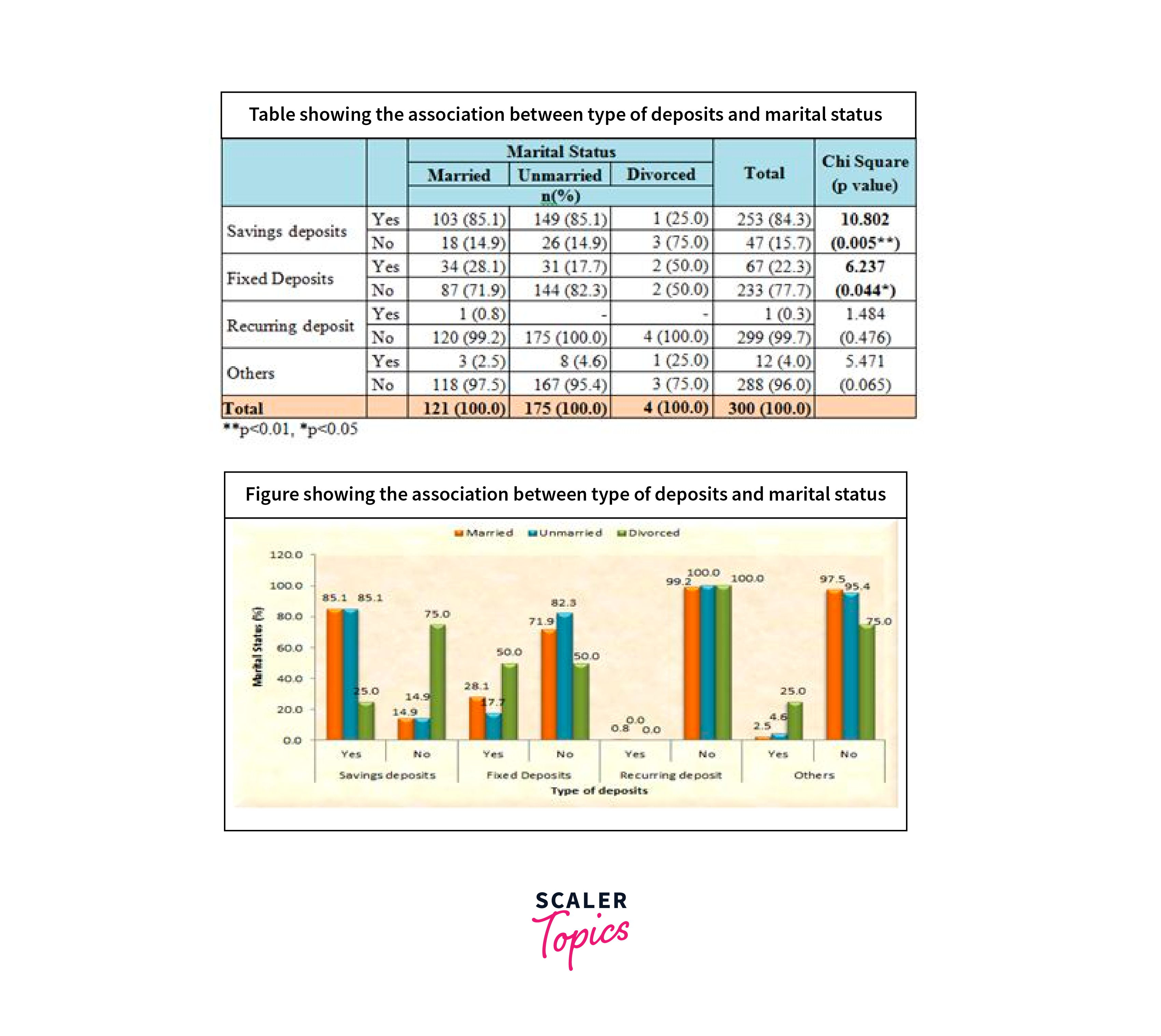
• Education: Researchers might apply the chi-square test to explore the relationship between student's academic performance and their participation in extracurricular activities.

Applications of Chi-Square Test

Applications of Chi-Square Test The application of chi square test spans across various fields, reflecting its versatility in analyzing categorical data. Here are some notable applications:

• Genetics: In genetics, the chi-square test is commonly used to analyze Mendelian inheritance patterns. Researchers apply the test to determine if observed genetic crosses align with the expected ratios, helping to understand gene expression and inheritance mechanisms.

• Market Research: Businesses frequently use the chi-square test to understand consumer behavior and preferences. By comparing observed customer responses against expected outcomes, companies can tailor their marketing strategies and product offerings to better meet market demands.

• Sociology: Sociologists apply the chi-square test to examine relationships between categorical variables in social research. This includes studies on demographic factors, social trends, and the impact of societal interventions.

• Medicine and Public Health: The test is instrumental in medical research for analyzing the efficacy of treatments or the distribution of health-related conditions across different populations, contributing to improved public health policies and interventions.

• Education: In educational research, the chi-square test helps in assessing the relationship between educational methods and learning outcomes, or exploring the association between demographic factors and educational achievements.

• Quality Control: In manufacturing and quality assurance, the chi-square test is applied to assess the conformity of product defects or failures to expected distributions, enabling companies to maintain quality standards and improve production processes.

When to Use?

The application of chi square test is most appropriate in specific scenarios where the data and research questions meet certain criteria. Here are key situations when the chi-square test is the preferred statistical analysis method:

• Categorical Data: The test is designed for use with categorical (nominal or ordinal) data, where observations can be classified into distinct categories.
• Independence Testing: It is used to determine if there is a significant association between two categorical variables, helping to assess the independence of these variables in a contingency table format.
• Goodness-of-Fit: When you want to compare observed frequencies in a single categorical variable with expected frequencies based on a theoretical distribution, the chi-square goodness-of-fit test is suitable.
• Large Sample Sizes: The application of chi-square test requires a sufficiently large sample size to ensure the validity of the chi-square approximation. A common rule of thumb is that all expected counts should be 5 or more.
• Non-Parametric Conditions: It is an ideal choice when the data does not meet the assumptions required for parametric tests, such as normality or homoscedasticity, because it does not rely on underlying distributional assumptions for the data.
• Multiple Categories: The test can be applied when dealing with multiple categories within variables, allowing for a broad analysis of how different categories relate to each other.

Advantages of Chi-Square Test

The application of chi-square test offers several key benefits, making it a popular choice for statistical analysis:

• Versatility: It can be used for both goodness-of-fit testing and testing for independence, making it highly versatile across various types of research questions involving categorical data.
• Non-Parametric: The test does not assume a normal distribution of the data, making it suitable for ordinal and nominal data where parametric assumptions are not met.
• Large Sample Sizes: It is effective for large sample sizes, providing robust results as the sample size increases, which is often the case in fields like market research and epidemiology.
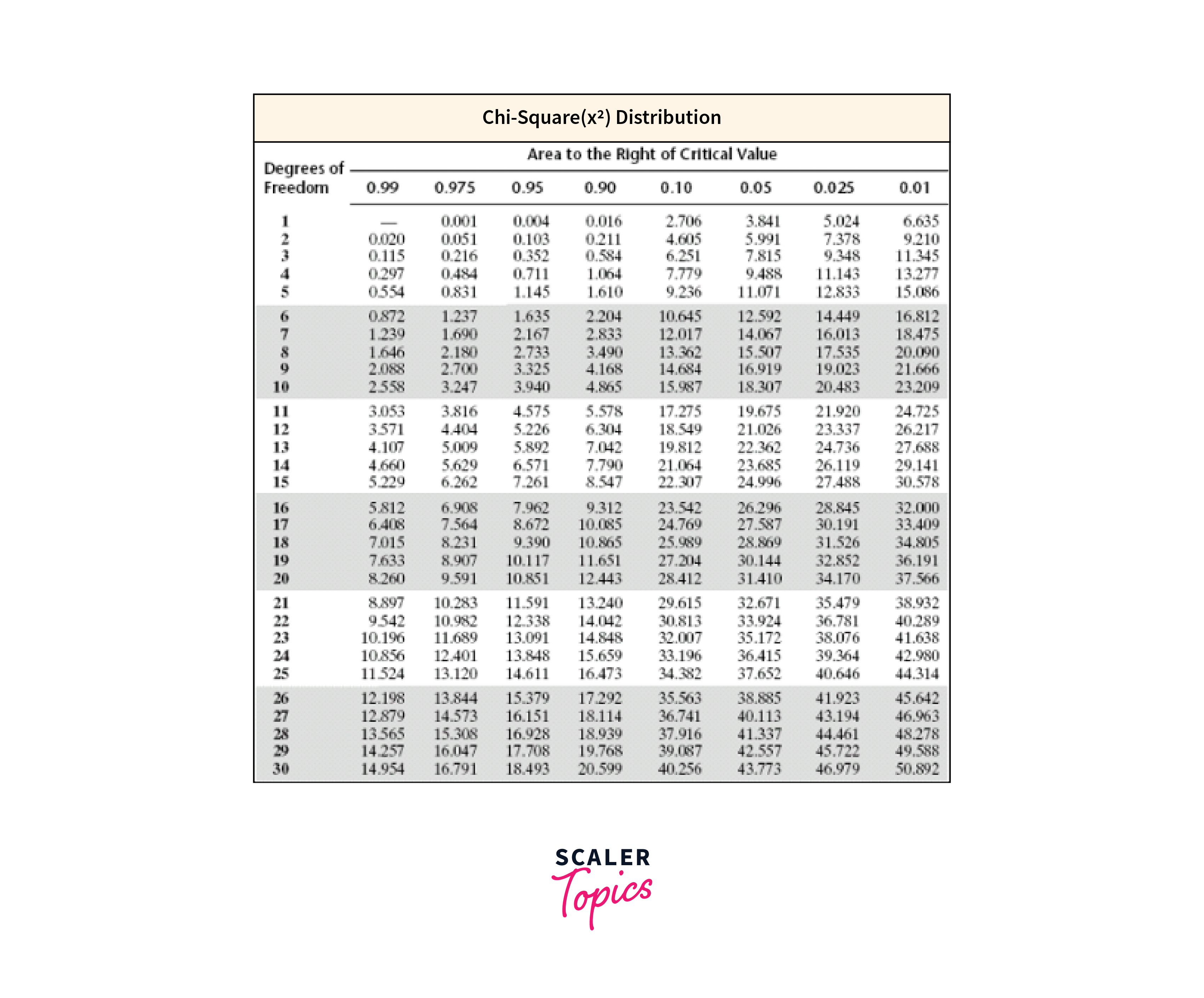
• Flexibility: The test can handle a wide range of applications, from market research to genetics, making it a flexible tool for analyzing categorical data across diverse disciplines.

Limitations of Chi-Square Test

Despite its widespread application, the chi-square test has several limitations that need to be considered:

• Sample Size Requirements: It may not be suitable for very small sample sizes, as expected frequencies below 5 in any category can lead to inaccuracies in results.
• Categorical Data Only: The test is limited to categorical data and cannot be used for continuous data without categorization, which might lead to loss of information.
• Independence Assumption: It assumes that observations are independent. In cases where data points are related or paired, the chi-square test's validity may be compromised.
• Over-simplification: While its simplicity is an advantage, it can also be a drawback as it might oversimplify complex relationships between variables, leading to misleading conclusions.
• No Directionality: The test can indicate whether variables are related but does not provide information about the direction or strength of the relationship, unlike some other statistical methods.