Armstrong Number - Scaler Topics

Abstract

The Armstrong number is the number whose sum of each digit of the number powered to its total digits count is equal to the given number. These numbers are also called Narcissistic numbers.

Introduction

"Maths is very interesting if you are eager to find the patterns". Armstrong number is also a pattern-based number. The Armstrong number is the number whose sum of each digit of the number powered to its total digit count is equal to the given number.

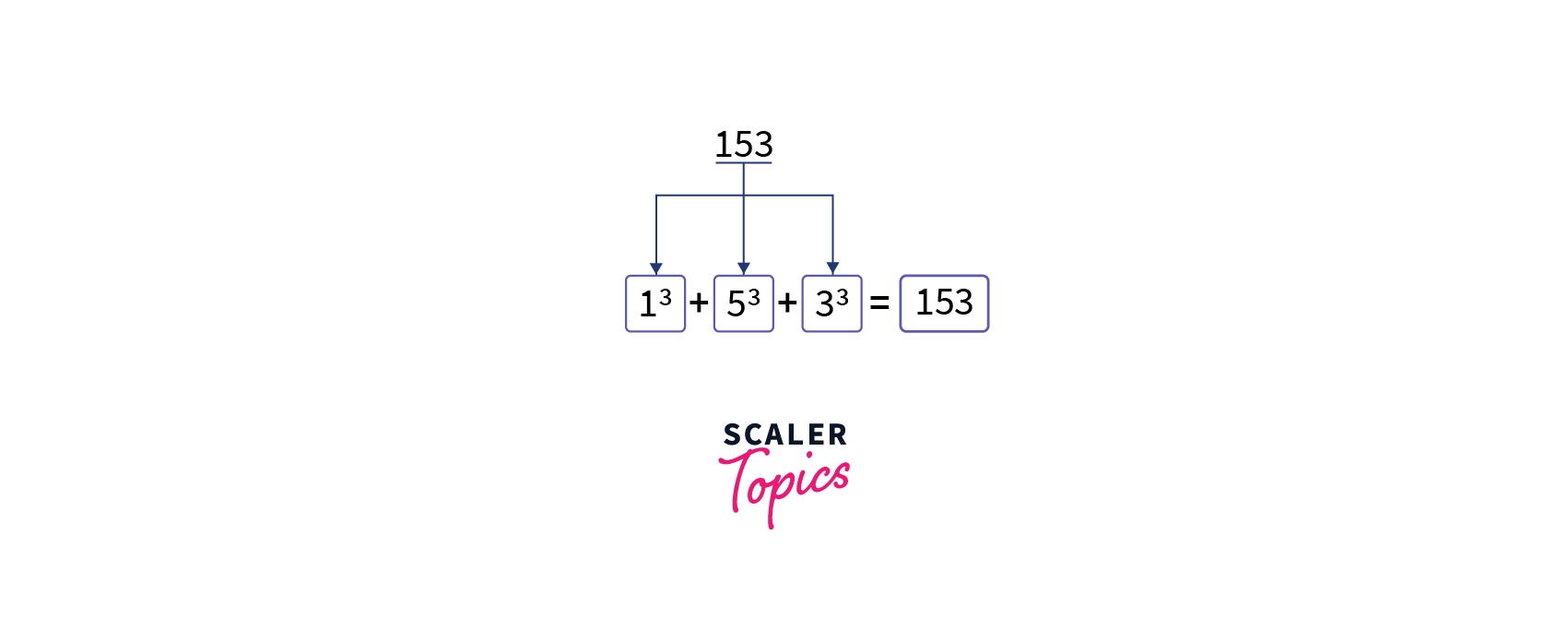
Example of Armstrong Number

The number 153 is an Amstrong number because the total digits in the number is 3 and the sum of 1^3+ 5^3 +3^3 is equal to the 153. The smallest positive Armstrong number is 1.

Example of Armstrong Number

Armstrong Number in C

Introduction: Let's try to find Armstrong numbers in the C programming language

1. Check Armstrong Number of three digits

Given a three-digit number we need to check whether the number is an Armstrong number or not. For example, 153 is an Armstrong number because the sum of digits raised to power 3 is equal to its own original number.

Intuition: We will divide the given three-digit number by the 10 until it becomes zero, find the remainder by taking the modulus of the number using 10, and multiply the remainder three times because the total number of digits in the number is 3, and store the sum is the variable say sum also we need to store the given number in the other variable also Because original number will become zero at the end.

Finally, we have to check the sum is equal to the given number(that is stored in the other variable say copyNumber), if they are equal the given three digit number is an Armstrong number otherwise not.

Algorithm:

Read the number and store this number in a copyNumber(So that we can compare the sum at the end).
Declare a sum variable and initialize it to zero.
For each digit of the number multiply each digit three times and add it to the sum variable.
Divide the number until the number becomes zero.
If the sum is equal to the copyNumber variable, it is an Armstrong number otherwise not an Armstrong number.

Let's try to implement the above algorithm in the C language.

Output:

In the above snippet, We are dividing the given three-digit number by the 10 until it becomes zero, and find the remainder by taking the modulus of the number using 10, and multiplying the remainder three times because the total number of digits in the number is 3, and store the sum is the variable say sum also we need to store the given number in the other variable also Because original number will become zero at the end.

Finally, we are checking whether the sum is equal to the copynumber if yes the number is an Armstrong number otherwise not.

Complexity

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers in order to check Armstrong numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

2. Check Armstrong Number of n digits

Given a number of n digits we need to check whether the number is an Armstrong number or not. For example, 1 is an Armstrong number but 11 is not an Armstrong number. We have to write code that works for any number of digits.

Intuition: First, we have to find the total number of digits in the given number, for this, We will divide the given number by 10 until it becomes zero and count the total digits because the total digits of the number are equal to the maximum number of times the number is divisible by 10 also before dividing the number we will then store the number is temporary variable say (copyNumber).

We will divide the copynumber variable by 10 until it becomes zero, and find the remainder by taking the modulus of the number using 10, and multiply the remainder totaldigits time that we have already calculated in the starting phase, and store the sum is the variable say sum also we need to store the given number in the other variable also Because original number will become zero at the end.

Finally, we have to check the sum is equal to the given number(that is stored in the other variable say copyNumber), if they are equal the given three-digit number is an Armstrong number otherwise not.

Let's try to write an algorithm first for checking Armstrong's number of n digits.

Algorithm:

Read the number from the user.
Get the total number of digits in the number
Save the total digits in a variable say digits.
For each digit of the number multiply each digit of the number digits(total number of digits) number of times and add the sum in the variable say sum.
Check if the sum equal to the original number.
If yes the number is an Armstrong number otherwise not an Armstrong number.

Let's try to implement the above algorithm in the C language.

Output:

In the above snippet, We are finding the total number of digits in the given number first and then dividing the given number by the 10 until it becomes zero, and find the remainder by taking the modulus of the number using 10, and multiplying the remainder total digit times, and store the sum is the variable say sum also we need to store the given number in the other variable also Because original number will become zero at the end.

Finally, we are checking whether the sum is equal to the copynumber if yes the number is an Armstrong number otherwise not.

The number 1653 is not an Armstrong number because 1^3 + 6^3 + 5^3+ 3^3 the sum of digits is equal to 1653 that's why it is not an Armstrong number.

Complexity

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

3. Check Armstrong Number using Functions

We need to check whether a number of any number of digits is an Armstrong number or not using user-defined functions which means we need to call a particular function that will check whether the number is an Armstrong number or not of different length. Let's try to write an Algorithm first.

Intuition: We will define a boolean function at first to check the Armstrong number of n length and in the user define function we have to find the total number of digits in the given number, for this, We will divide the given number by 10 until it becomes zero and count the total digits because the total digits of the number are equal to the maximum number of times the number is divisible by 10 also before dividing the number we will then store the number is temporary variable say (copyNumber).

Algorithm:

Read the number and call a user-defined method to check whether the number is an Armstrong number or not.
In the method store this number in a copyNumber variable.
Declare a sum variable and initialize it to zero.
For each digit of the number multiply each digit three times and add it to the sum variable.
Divide the number until the number becomes zero.
If the sum is equal to the copyNumber variable, return the true number otherwise return false.

Let's implement the above algorithm in the C language.

Output:

In the above check_Armstrong boolean function, We are finding the total number of digits in the given number first and then dividing the given number by the 10 until it becomes zero, and find the remainder by taking the modulus of the number using 10, and multiplying the remainder total digit times, and store the sum is the variable say sum also we need to store the given number in the other variable also Because original number will become zero at the end.

Finally, we are checking whether the sum is equal to the copynumber if yes the number is an Armstrong number otherwise not. The 134 is not an Armstrong number because the sum of 1^3 + 3^3 +4^3 is not equal to the 134.

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

4. Check Armstrong from 1 to 1000

We need to check and print all Armstrong numbers from the range 1 to 1000. Let's first try to write an algorithm to check Armstrong's number from 1 to 1000.

The intuition is same as in the above case

Algorithm:

We need to find the Armstrong numbers present in the range [1-1000].
Run a loop from 1 to 1000
For ith element call a user-defined method to check whether the ith number is Armstrong number or not.
In the method store this number in a copyNumber variable.
Declare a sum variable and initialize it to zero.
For each digit of the number multiply each digit three times and add it to the sum variable.
Divide the number until the number becomes zero.
If the sum is equal to the copyNumber variable, return the true number otherwise return false.
If the user-defined function returns true, the number is an Armstrong number.

Let's try to implement the above algorithm in the C language.

Check Armstrong from 1 to 1001 2 is an Armstrong number 3 is an Armstrong number 4 is an Armstrong number 5 is an Armstrong number 6 is an Armstrong number 7 is an Armstrong number 8 is an Armstrong number 9 is an Armstrong number 153 is an Armstrong number 370 is an Armstrong number 407 is an Armstrong number

Complexity:

Time Complexity: The Time Complexityof the above approache is O(n).
Space Complexity: The Space Complexity of all the above approache is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

Armstrong Number in Java

Introduction: Here we will write different kinds of methods to find or check the Armstrong numbers in the java language.

1. Check Armstrong Number for 3 digit number

Given a three-digit number we need to check whether the number is an Armstrong number or not.

For example, 153 is an Armstrong number because the sum of digits raised to power 3 is equal to its own original number.

The Algorithm is the same as we discussed in the section of C programming language to check Armstrong number for 3 digits.

Let's implement the above algorithm in the Java language.

Output:

The 153 number is an Armstrong number because the sum of 1^3 +5^3 + 3^3 is equal to its own number.

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

2. Check Armstrong number for n digits

Given a number of n digits we need to check whether the number is an Armstrong number or not. For example, 1 is an Armstrong number but 11 is not an Armstrong number. We have to write code that works for any number of digits. Let's try to write an algorithm first for checking Armstrong's number of n digits.

Algorithm: The Algorithm is the same as we discussed in the section of the C programming language.

Let's implement the above algorithm in the Java language.

Output:

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

3. Check Armstrong number using For loop

Given a number, we need to check whether the number is an Armstrong number or not using For Loop. Let's write an Algorithm first to check a number is an Armstrong number or not.

Algorithm:

Read the number from the user.
Convert the number to the String type and get the length of the String using length() method of the String class.
Now use a for loop and iterate every character of the String, and for every character multiply each character by length(Total length of the String) times and store the sum in a variable, let's say sum.
Check if the sum is equal to the number then the number is an Armstrong number otherwise not.

Let's try to implement the above algorithm in the java language.

Output:

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers inorder to check Armstrong numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers. The 153 number is an Armstrong number because the sum of 1^3 +5^3 + 3^3 is equal to its own number.

4. Check Armstrong number using While loop

Given a number, we need to check whether the number is an Armstrong number or not using the while loop. Let's write an Algorithm first to check a number is an Armstrong number or not.

Algorithm:

Read the number from the user.
Convert the number to the String type and get the length of the String using the length() method of the String class.
Store the number in the copyNumber variable.
Divide the number until it becomes zero, and for every digit multiply the digit by total length times and store the sum in a variable.
if the value of the copyNumber and the sum is equal then the number is an Armstrong number otherwise not.

Let's implement the above algorithm in the java language.

Output:

The 150 is not an Armstrong number because the sum of 1^3 + 5^3 +0^3 is not equal to 150.

Complexity:

Time Complexity: The Time Complexity of all the above approache is O(n), Because we are simply iterating on the number.
Space Complexity: The Space Complexity of all the above approache is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

Armstrong Number in Python

Introduction: Here we will write different kinds of methods to find or check the Armstrong numbers in the python language.

1. Check Armstrong number for 3 digits.

Given a three-digit number we need to check whether the number is an Armstrong number or not. For example, 153 is an Armstrong number because the sum of digits raised to power 3 is equal to its own original number.

Algorithm:

The Algorithm is the same as we discussed in the section of C programming language to check Armstrong number for 3 digits.

Let's try to implement the above algorithm in the python language.

Output:

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

2. Check Armstrong number of n digits

Given a number of n digits we need to check whether the number is an Armstrong number or not . For example, 1 is an Armstrong number but 11 is not an Armstrong number. We have to write code that works for any number of digits. Let's try to write an algorithm first for checking Armstrong's number of n digits.

Algorithm: The algorithm is the same as the one we have used for Armstrong number of 3 digits in C language

Let's try to implement the above algorithm in the python language.

Output:

3. Check if the given number is Armstrong or not

Given a number we need to check whether the given number is Armstrong's number or not.

Let's try to write an Algorithm to check the number is Armstrong or not.

Algorithm: The Algorithm is the same as we discussed in the section of java programming language to check Armstrong number for n digits.

Let's try to implement the above algorithm in the python language.

Output:

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

4. Is 371 an Armstrong number?

Let's try to check whether the number 371 is an Armstrong number or not. At First, we will try to write an Algorithm to check whether the 371 is an Armstrong number or not.

Algorithm: The Algorithm is the same as we discussed in the section of C programming language to check Armstrong number for 3 digit.

Implementation of the above-dicussed algorithm in python language.

Output:

Complexity:

Time Complexity: The Time Complexity of all the above approaches is O(n`),Because we are simply iterating on the number.
Space Complexity: The Space Complexity of all the above approaches is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

Armstrong Number in C++

Introduction: Here we will write different kinds of methods to find or check the Armstrong numbers in the C++ language.

1. Check Armstrong Number of 3 Digits

Algorithm: The Algorithm is the same as we discussed in the section of the C programming language to check Armstrong's number for 3 digits.

Let's try to implement the above algorithm in the C++ language.

Output:

Complexity:

Time Complexity: The Time Complexity of the above approache is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approache is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

2. Check Armstrong Number of n Digits

Algorithm: The Algorithm is the same as what we discussed in the C programming language section.

Let's try to implement the above algorithm in the C++ language.

Output:

Complexity:

Time Complexity: The Time Complexity of the above approache is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approache is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

Check Armstrong Number using For loop

Given a number, we need to check whether the number is an Armstrong number or not using For Loop. Let's write an Algorithm first to check a number is an Armstrong number or not.

Algorithm: The Algorithm is the same as we discussed in the section of java language.

Let's try to implement the above algorithm in the C++ language.

Output:

Complexity:

Time Complexity: The Time Complexity of the above approache is O(n), Because we are simply iterating on the numbers inorder to check Armstrong numbers.
Space Complexity: The Space Complexity of the above approache is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

Check Armstrong Number using a do-while loop

Given a number, we need to check whether the number is an Armstrong number or not using do-while Loop. Let's write an Algorithm first to check a number is an Armstrong number or not. Algorithm:

Read the number from the user.
Find the total number of digits in the number using the do-while loop by dividing the number 10 until it did not become equal to 10.
Store the number in the copyNumber variable.
Divide the number until it becomes zero using a do-while loop, and for every digit multiply the digit by total length times and store the sum in a variable.
if the value of the tempvariable and the sum is equal then the number is an Armstrong number otherwise not.

Let's try to implement the above algorithm using C++ language.

Output:

Complexity:

Time Complexity: The Time Complexity of all the above approaches is O(n), Because we are simply iterating on the number .
Space Complexity: The Space Complexity of all the above approaches is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

Armstrong Number in JavaScript

Introduction: Here we will write different kinds of methods to find or check the Armstrong numbers in the javascript language.

1. JavaScript code to check number is Armstrong or not

Given a number, n we have to check whether the number is an Armstrong number or not. For example, 153 is an Armstrong number because the sum of the digits raised to power 3(length of the number ) is equal to the number. Let's try to write first an Algorithm for how to check number is Armstrong or not in javascript (Node.js).

Algorithm:

The Algorithm is the same as what we discussed in the section of java programming section to check Armstrong’s number for n digit

Let's try to implement the above algorithm in the javascript.

Output:

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

2. Check Armstrong Number of Three Digits

Given a three-digit number we need to check whether the number is an Armstrong number or not.

For example, 153 is an Armstrong number because the sum of digits raised to power 3 is equal to its own original number.

The Algorithm to check three-digit numbers is the same as we discussed above in the C language.

Let's try to implement the above algorithm in javascript language.

Output:

The Number 123 is not an Armstrong number because 1^2 +2^ 2 + 2^3 is not equal to 123.

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

3. Check Armstrong Number of n Digits

Algorithm: The Algorithm is the same as what we discussed in the section of java programming section to check Armstrong's number for n digit..

Let's try to implement the above algorithm in javascript language.

Output:

The Number 12 is not an Armstrong number because 1^2 +2^ 2 is not equal to 12.

Complexity:

Time Complexity: The Time Complexity of the above approach is O(n), Because we are simply iterating on the numbers.
Space Complexity: The Space Complexity of the above approach is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

Check Armstrong Number using while loop

Given a number, n we have to check whether the number is an Armstrong number or not using the while loop. For example, 153 is an Armstrong number because the sum of the digits raised to power 3(length of the number ) is equal to the number. Let's try to write first an Algorithm for how to check number is Armstrong or not in javascript (Node.js).

Algorithm: The Algorithm is the same as we discussed in the section of java language.

Let's try to implement the above algorithm in javascript language.

Output:

The Number 12 is not an Armstrong number because 1^2 +2^ 2 is not equal to 12.

Complexity:

Time Complexity: The Time Complexity of all the above approaches is O(n), Because we are simply iterating on the number.
Space Complexity: The Space Complexity of all the above approaches is O(1), Because the amount of memory that we use is constant, we don't use any extra dynamic datatype for storing the numbers.

Conclusion

Armstrong number is equal to the sum of the digit raised to power its length.
These numbers are also called Narcissistic numbers