Adversarial Search in Artificial Intelligence

Introduction

The development of algorithms and tactics for making decisions in competitive settings where numerous agents or players have competing interests is the focus of adversarial search in artificial intelligence. Finding the optimum movements or actions for a player while accounting for opponents' actions and prospective responses is the major objective of the adversarial search.

The objective of the adversarial search is to create intelligent algorithms that can choose the best course of action under conflicting circumstances while taking into account the moves of rivals and their potential retaliations. To find the optimum move or action to make, adversarial search algorithms often search through a game tree, which represents all feasible game states and their transitions.

Overall, adversarial search is a difficult and significant field of AI that calls for a thorough knowledge of game theory, decision-making processes, and optimization strategies(such as mixed strategies). It has uses across many industries and is still being actively researched in the realm of artificial intelligence.

Types of Games in AI

In the field of artificial intelligence (AI), a variety of games are frequently employed for algorithmic game-playing research, development, and testing. The following are some of the common game genres in AI:

a. Perfect Information

Perfect information games are those in which every participant always has perfect knowledge of the game's current state. In other words, no information is concealed or unknown in perfect information games, and all players are aware of the current state of the game, including the locations of all pieces, cards, and other game components. Games like chess, checkers, and Othello (also known as Reversi), in which every player has complete knowledge of the board and every piece's location, are examples of perfect information games. Players in these games have a complete awareness of the present state of the game and can make judgments based on knowledge of all potential moves and their effects.

b. Imperfect Information

In the field of artificial intelligence (AI), imperfect information games are those in which participants do not have complete knowledge of the game state and where there is concealed information, uncertainty, or unknowns that influence the decision-making process. These games require players to make judgments based on partial or erroneous knowledge since some components of the game state are not visible or known to all players. Poker and many other real-world strategy games are examples of imperfect information games where participants have secret cards, personal information, or unknown factors that affect the game's result. Players must infer or guess the hidden information in these games based on the actions and behaviors of their opponents because they do not have complete visibility of the entire game state.

c. Deterministic Games

In artificial intelligence (AI), deterministic games are those in which the results of actions are entirely predetermined and foreseeable. In deterministic games, there is neither randomness nor uncertainty; rather, the outcomes of actions are known with certainty. Traditional board games like tic-tac-toe are examples of deterministic games, where the outcome of each move is entirely determined by the game's rules and the state of the playing board at the time. No unpredictability is present in these games, and every action's result can be exactly computed or predicted.

d. Non-deterministic Games

Non-deterministic games are those in which there is a certain amount of unpredictability or ambiguity in how things will turn out. In non-deterministic games, actions cannot be foreseen with certainty and their outcomes may vary depending on probabilistic circumstances. Games of chance like poker, blackjack, and backgammon are examples of non-deterministic games. In these games, the results of each move or action are determined by random events like shuffled card decks, dice rolls, or random events. In these games, players must make judgments based on probability, risk analysis, and strategic planning because they lack complete knowledge of the game state and the potential results of their actions.

Zero-Sum Game

According to game theory, a zero-sum game is one in which each player's overall winnings or losses are equal to zero. In other words, every profit made by one player is offset by an equivalent loss suffered by another, leaving no money on the table overall. The interests of the players are wholly at odds with one another in a zero-sum game, and the overall reward is fixed.

The reward matrix, which depicts each player's outcomes or payouts based on their strategies, has the property that the sum of payouts for all players at any given outcome is zero in a zero-sum game. This means that any increase in one player's payout must be offset by a corresponding decrease in another player's payoff.

Many traditional board games, including chess, checkers, and go, are examples of zero-sum games. In these games, the outcome is entirely controlled by the strategies and actions of the players, and one player's gain always comes at the expense of the other player's loss. Numerous competitive scenarios, such as bidding in auctions, discussions, and sporting events, are other instances.

Zero-Sum Game: Embedded Thinking

The concept of zero-sum games can also be extended to the idea of embedded thinking in the context of game theory and artificial intelligence.

When people see situations or problems in isolation, without taking into account the larger context or the interdependencies with other aspects, this is referred to as embedded thinking. It is a form of limited thinking that only considers the short-term repercussions or benefits, ignoring any potential long-term ramifications or implications.

Embedded thinking can result in inferior strategies or choices in zero-sum games. Players in a zero-sum game frequently concentrate on maximizing their gains and limiting those of their opponents, with the understanding that any gain made by one player must be at the price of another. This ingrained way of thinking might result in a completely antagonistic mindset, where participants are only concerned with outsmarting and destroying their rivals and don't think about alternative possible cooperative or strategic outcomes.

Formalization of the Problem

Formalization of the problem in Adversarial Search is the process of defining the problem mathematically. This involves specifying the rules of the game, the players, the available actions, and the outcome of the game. The following elements are often included in the formalization:

a. Initial State

The starting configuration of the game before any moves have been taken by the players is referred to as the initial state in the formalization of the problem in the adversarial search. It stands for the starting game state from which the game is played. Information like the starting placements of the game pieces, scores, and other crucial game-related data are frequently included in the beginning state. The starting locations of the chess pieces on the board, for instance, would be the first state in a game of chess. The opening state in a card game like poker entails dealing each player with their initial hand of cards.

b. Player(s)

Players are the agents or entities that take part in the game in the adversarial search formalization of the problem. Players are frequently portrayed as decision-makers who make choices within the game to accomplish their goals or increase their rewards. There may be more than two participants and they may each have a separate role or goal in more complicated games. Defining each player's actions, rewards, and strategies as well as creating algorithms that enable each player to make the best choices possible at each stage of the game constitutes the formalization of the problem in the adversarial search. Depending on the complexity of the game and the desired degree of performance, players' decision-making algorithms, also known as strategies, can range from straightforward rules-based to more complex algorithms.

c. Action(s)

Actions reflect the potential moves or decisions a player may make from a specific game state in the formalization of adversarial search in artificial intelligence. At each decision point in the game, a player has an option, or actions, which define the potential transitions to new game states. The collection of options open to a player at a specific game state depends on the regulations and limitations of the particular game being modeled.

Typically, actions in the formalization of the problem exhibit the following traits:

• Deterministic or Stochastic
• Legal or Illegal
• Player-Specific
• Finite or Infinite
• Hierarchical or Sequential
• Strategic or Tactical

d. Result(s, a)

When a player makes a specific action "a" from a predetermined state "s" in the game, Result(s, a) represents the outcome or resulting state in the adversarial search formalization of the problem. It denotes how an action ("a") affects the current ("s") to produce a new state.

In the context of adversarial search, the idea of "Result(s, a)" is crucial because it enables players to model the effects of various actions and assess how desirable the subsequent states are. By taking into account the possible outcomes and payoffs linked to various actions and states, this knowledge is essential for decision-making algorithms to decide the optimal course of action to pursue in a game.

e. Terminal-Test(s)

A crucial element in the formalization of the problem in adversarial search in artificial intelligence is a terminal test, sometimes referred to as a goal test. It is a function that determines if a specific game state is a terminal state, that is, a state at which the game has ended and each player has received their payment. It helps game-playing algorithms determine when a round is over and no more moves or actions are permitted.

As no additional actions need to be investigated beyond terminal states, the terminal test also aids in reducing the search area, which can significantly increase the effectiveness of the game-playing algorithms.

f. Utility(s, p)

The measure of desire or preference that a player attributes to various outcomes or payoffs in the game is referred to as utility in the formalization of the problem in adversarial search in artificial intelligence. The utility, which is used to measure a player's subjective preferences, is frequently expressed as a number value connected to each potential result or payoff. As it enables players to communicate their preferences and make judgments based on those preferences, it is a crucial idea in game theory and decision theory. In the game, players try to maximize their usefulness or accomplish their strategic goals.

Game Tree

A game tree is a visual representation of every action and consequence that can be made in a two-player game when using adversarial search in artificial intelligence. The game tree begins with the beginning state of the game, and each node in the tree represents a different state of the game. These states include details about which player is taking their turn, the layout of the board, and other pertinent information.

The game tree is frequently used in conjunction with search algorithms like minimax or alpha-beta pruning to determine a player's best course of action under the assumption that the other player would play similarly well. The search algorithm can decide the best move for a player by examining the game tree and considering all feasible moves and outcomes.

a. Example

Consider Amy and Bob playing the rock-paper-scissors game against each other. Each participant in this game simultaneously selects one of the three possibilities, rock, paper, or scissors.

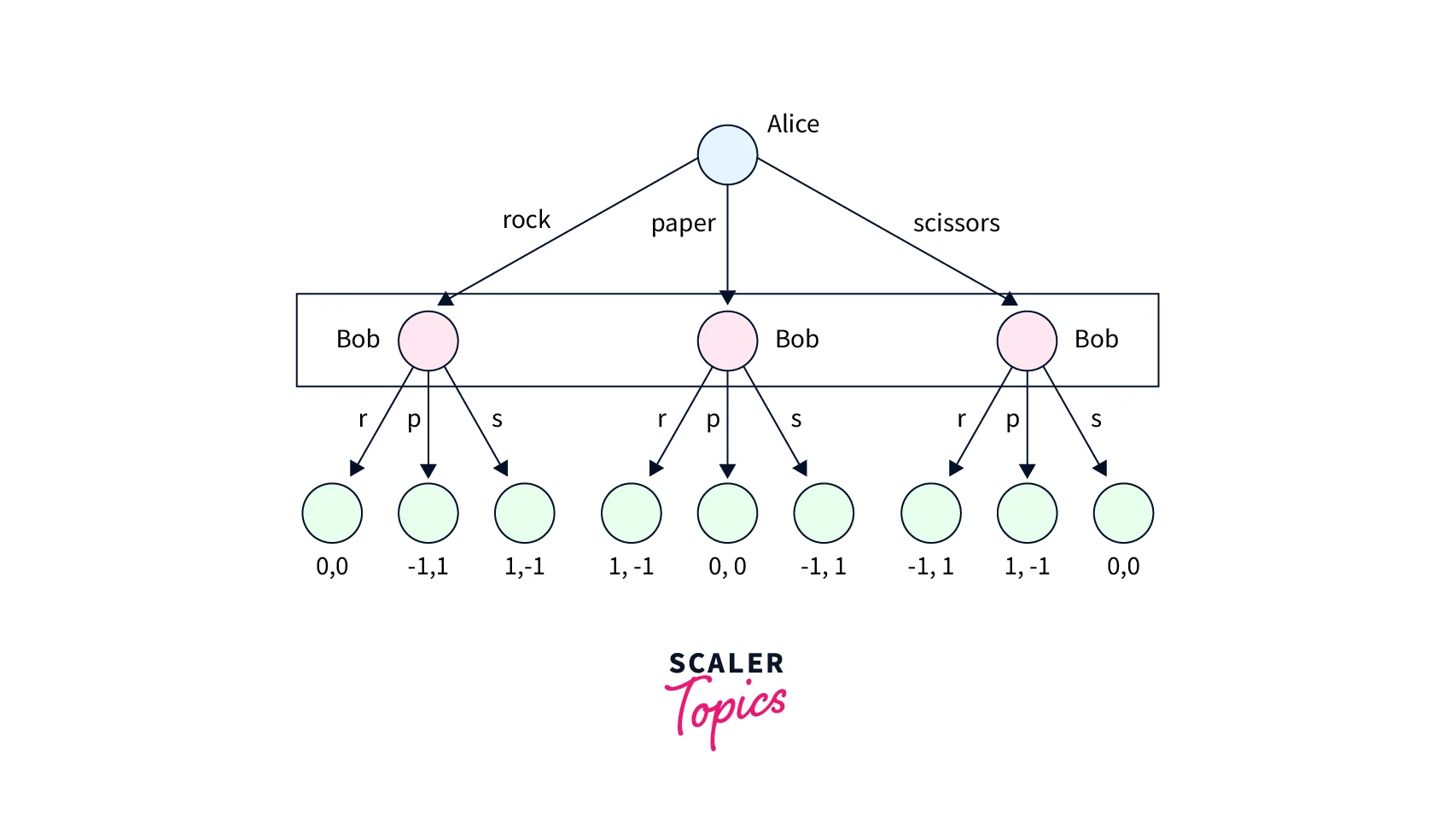
Now, depending on what each of the two kids selects, either one of them wins the game, or it ends in a draw. The following are the game's rules. The game ends in a tie if both players select the same course. If one decides to rock and the other to write, the latter will win. One wins if they opt to rock while the other decides to use scissors. Scissors win if one selects paper and the other, (Rock smashes scissors) scissors. Let's think about the rewards now (paper gets cut with scissors). Assume that a youngster receives a penny (+1) for winning, a penny (-1) for losing, and a penny (0) for a draw.

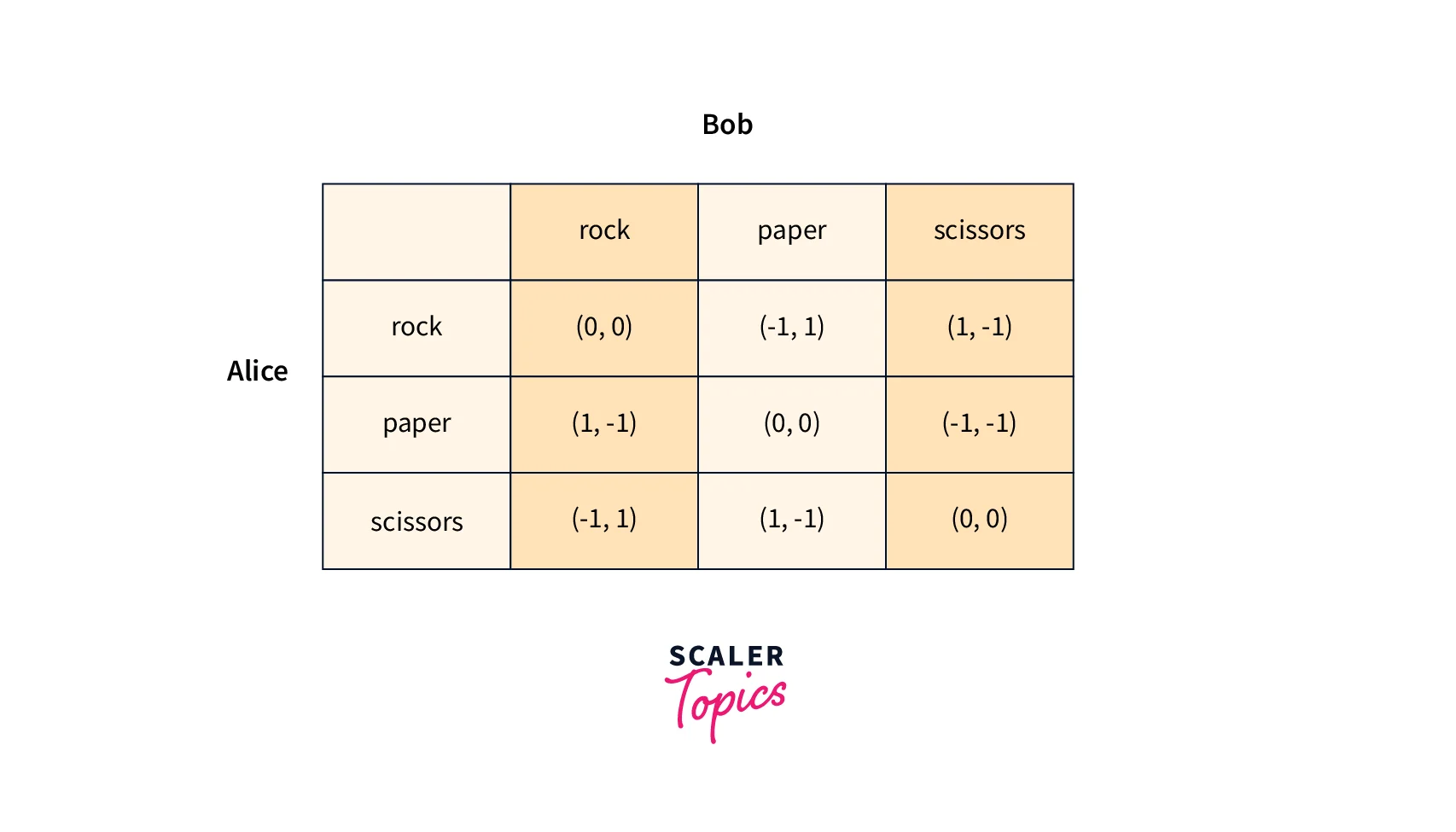
• The collection of "strategy profiles" or "strategy arrays" comprises a 3 X 3 table because there are two players in this game and each has three available strategies.

• Amy's techniques are listed as rows in the table in the preceding picture, and Bob's strategies are listed as columns.

• There are two payouts for the two players for each of the nine cells in the table, with Amy and Bob receiving their payouts first. As an illustration, if Amy selected to play "rock" (row 1) and Bob opted to play "scissors" (column 3), Amy would win a penny while Bob would lose a penny.

b. Example Explanation

This type of game can be solved formally by employing the idea of mixed strategies. Consider how Amy or Bob may perform. If you had previously played this game, you would be aware that choosing to play either rock, paper, or scissors each time makes you predictable and susceptible to your opponent.

Bob just needs to play paper if Amy played rock in every trial. Similarly, if Bob played paper in every trial, Amy would just need to play scissors to win every round. As a result, it would appear that the best strategy for this game is to be surprising in each round, switching between playing paper and rock.

Important Features of Adversarial Search

An important area of research in artificial intelligence is adversarial search, which deals with decision-making in hostile situations. The following are some crucial aspects of adversarial search:

Perfect or Imperfect Information

You can categorize adversarial games as having perfect or imperfect information. In games with perfect information, every player is fully aware of the game's current state; however, in games with imperfect information, certain information is kept secret from the players.

Adversarial Search Algorithms

In adversarial games, search techniques like minimax and alpha-beta pruning are employed to determine the optimum move. By weighing the possible results of every move, these algorithms assist in determining the optimum move for a player.

Thumb Rule

Due to the size of the game tree, it may occasionally not be able to search it completely. Heuristics are utilized in these situations to approximate the optimum move. Heuristics are shortcuts that let the algorithm evaluate a move's potential rapidly without having to look through the complete game tree.