Decentralized pomdp

Introduction

Decentralized Partially Observable Markov Decision Process (Dec-POMDP) is a mathematical framework that is commonly used for decision-making in multi-agent systems. In contrast to single-agent decision-making, where one agent interacts with an environment, Dec-POMDP enables a group of agents to interact with an environment and each other. Dec-POMDP is an extension of the Partially Observable Markov Decision Process (POMDP) model, which is used for decision-making in single-agent systems.

In a Dec-POMDP, each agent has access to its observations and actions but not to the observations and actions of other agents. Therefore, the agents must communicate with each other to coordinate their actions and make optimal decisions. The goal of a Dec-POMDP is to find a joint policy that maximizes the expected cumulative reward for all agents while considering the uncertainty about the state of the environment and the actions of other agents.

What is a Decentralized POMDP?

In Dec-POMDP, the agents share a common objective, but each agent has its own partially observable state, action space, and observations. The agents interact with the environment through their actions and receive observations based on their own partially observable state. Due to communication constraints and the limitations of sensor observations, agents may have an incomplete understanding of the global state of the system and the actions of other agents.

The goal of Dec-POMDP is to find a joint policy that maximizes the expected long-term reward for the team of agents. A joint policy is a mapping from the individual observations and partially observable states of each agent to a joint action that the team should take at that time step. The joint policy should be robust to communication uncertainties and take into account the cost and delay of communication between agents.

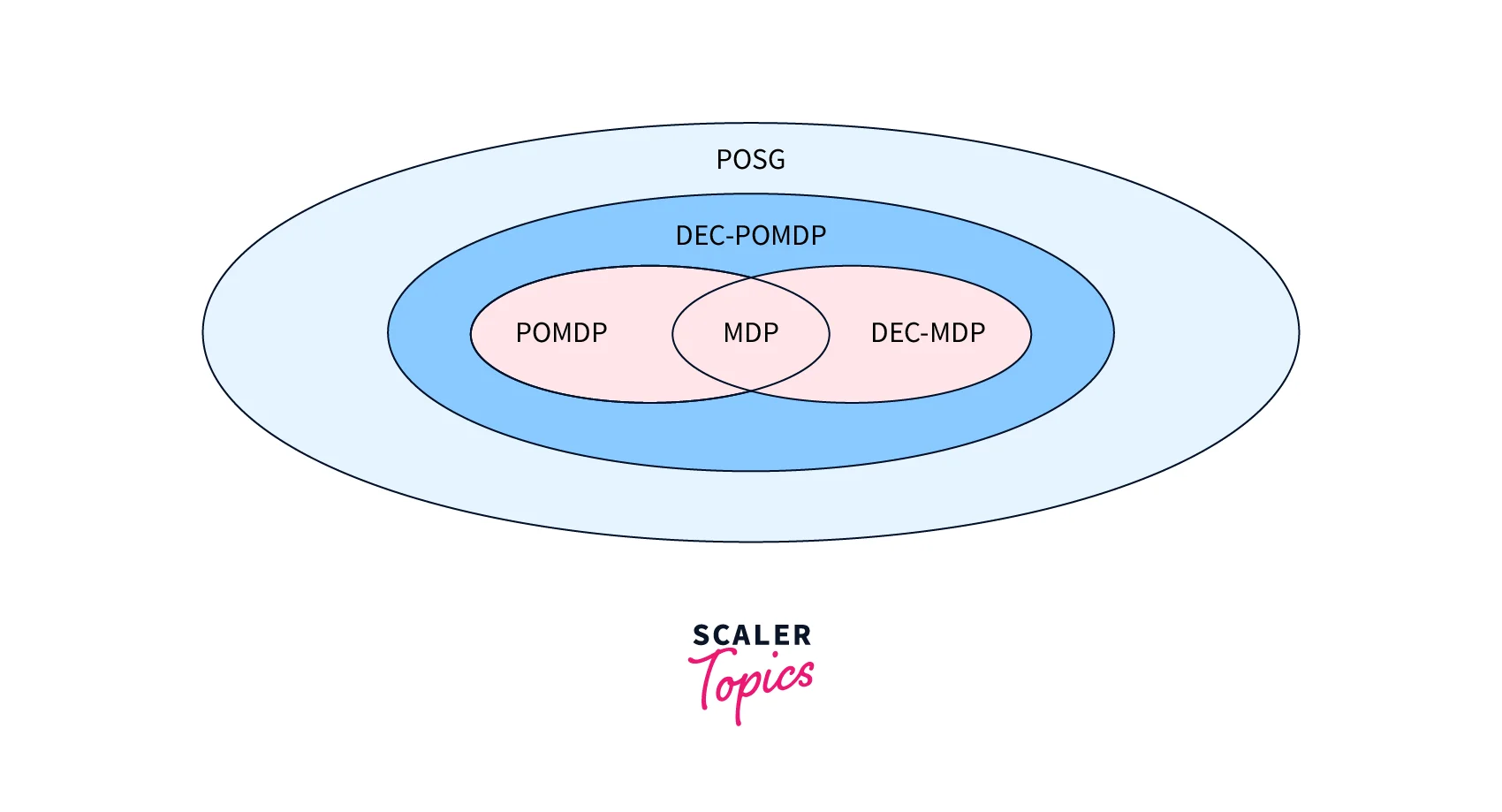
A Markov decision process (MDP) and a partially observable Markov decision process (POMDP) are generalized to take into account several dispersed agents.

Introduction

Decentralized Partially Observable Markov Decision Process (Dec-POMDP) is a decision-making framework that is commonly used in multi-agent systems. In a Dec-POMDP, a group of agents interacts with an environment and each other to make optimal decisions based on the observations and actions available to them. The agents must coordinate their actions to maximize the expected cumulative reward while taking into account the uncertainty about the environment and the actions of other agents.

A Simple Example

To understand Dec-POMDP, let's consider a simple example of a warehouse that needs to be managed by two robots. The robots can only observe their immediate surroundings and take actions to move boxes from one location to another. The warehouse environment is uncertain, and the actions of one robot may affect the actions and observations of the other robot.

In this scenario, a Dec-POMDP model can be used to determine the optimal joint policy for the robots to maximize their rewards. The agents need to coordinate their actions to ensure that they don't interfere with each other's work and complete their tasks as quickly as possible.

To solve this problem, the agents need to exchange information with each other to update their beliefs about the environment and other agents' actions. The Dec-POMDP model takes into account the uncertainty about the state of the environment and the actions of other agents to generate an optimal joint policy for the agents to follow.

Defining a Decentralized POMDP

A Dec-POMDP can be defined as a tuple (S, A, O, T, R, Z, N), where:

• S is a set of possible states of the environment.
• A is a set of possible actions that agents can take.
• O is a set of possible observations that agents can make.
• T is a transition function that defines the probability distribution over the next state, given the current state and action.
• R is a reward function that defines the expected reward for each state-action pair.
• Z is an observation function that defines the probability distribution over the observations given the current state and action.
• N is the number of agents in the system.

Dec-POMDP assumes that each agent has its observation function and action set, but they don't have access to other agents' observations and actions. Therefore, the agents need to communicate with each other to coordinate their actions and make optimal decisions.

Solving a Dec-POMDP involves finding a joint policy that maximizes the expected cumulative reward for all agents while considering the uncertainty about the environment and other agents' actions. Decentralized POMDP algorithms, such as Decentralized Value Iteration, Decentralized Policy Iteration, and Decentralized Monte Carlo Planning, are commonly used to solve Dec-POMDP problems.

Decentralized POMDP Algorithms

Several algorithms can be used to solve Decentralized Partially Observable Markov Decision Process (Dec-POMDP) problems. These algorithms aim to find the optimal joint policy for all agents that maximizes the expected cumulative reward while taking into account the uncertainty about the environment and other agents' actions.

Some of the commonly used Decentralized POMDP algorithms are:

• Decentralized Value Iteration (DVI): DVI is an iterative algorithm that computes the optimal joint value function for all agents. It involves propagating the value function updates from each agent to its neighbouring agents until convergence. DVI can handle large-scale Dec-POMDP problems but is computationally expensive.
• Decentralized Policy Iteration (DPI): DPI is an iterative algorithm that computes the optimal joint policy for all agents. It involves iteratively improving the policies of each agent until convergence. DPI is computationally less expensive than DVI but requires a larger amount of communication between agents.
• Decentralized Monte Carlo Planning (DMCP): DMCP is a sampling-based algorithm that generates a set of joint action sequences and evaluates them to find the optimal joint policy. It uses a tree-based search approach to sample and evaluate the action sequences. DMCP is computationally efficient but may not guarantee convergence to the optimal solution.
• Decentralized Particle Belief Propagation (DPBP): DPBP is a message-passing algorithm that uses particle filtering to estimate the joint belief of all agents. It involves propagating the belief updates from each agent to its neighbouring agents until convergence. DPBP can handle large-scale Dec-POMDP problems but may not guarantee convergence to the optimal solution.

Applications of Decentralized POMDP

Decentralized Partially Observable Markov Decision Process (Dec-POMDP) has a wide range of applications in different fields, including:

• Robotics: Dec-POMDP is widely used in robotics for tasks such as coordinated movement, exploration, and surveillance. , For example,, a team of robots can coordinate their actions to explore an unknown environment efficiently.
• Autonomous Systems: Dec-POMDP is also used in autonomous systems such as self-driving cars and unmanned aerial vehicles. These systems need to make decisions based on uncertain environments and interact with other agents, making Dec-POMDP a suitable framework for decision-making.
• Game Theory: Dec-POMDP can be applied to game theory to model decision-making in competitive environments where multiple agents interact to maximize their rewards.
• Communication Networks: Dec-POMDP can be used to optimize communication networks, where multiple agents interact to maximize network performance and minimize congestion.
• Multi-Agent Reinforcement Learning: Dec-POMDP can be used in Multi-Agent Reinforcement Learning (MARL), where multiple agents learn to make decisions by interacting with an environment and each other.