Monte Carlo tree search

Introduction

Monte Carlo Tree Search (MCTS) is a well-known technique for resolving problems relating to decision-making. It has been successfully used in games like Go and chess to search through all possible moves in a game tree using Monte Carlo simulations. MCTS has also been used in various industries, including robotics and driverless cars.

What is Monte Carlo Tree Search in AI?

Monte Carlo Tree Search (MCTS) is a search algorithm in the field of AI employed in game-playing and decision-making processes. MCTS is probabilistic and heuristic-driven and uses random simulations to explore the decision tree and make well-informed choices. It blends the traditional tree search implementations with reinforcement learning concepts.

In a tree search algorithm, it is always possible that the best action in the present situation isn't the most appropriate. The MCTS algorithm is helpful in these situations because it keeps testing several other strategies in parallel to the currently thought-to-be optimal strategy. This keeps on happening throughout the learning phase of the algorithm. This feature is known as the exploration-exploitation trade-off. It uses the actions and methods that have been determined to be the best, but it also has to keep looking into the local space for potential alternatives to see whether they could replace the best.

The exploration phase helps explore and locate the unknown areas of the tree, which may lead to the discovery of a more efficient path. In other words, the exploration phase leads to more growth of the breadth of the tree rather than its depth. Thus exploration strategy of  MCTS ensures that it is not missing any potentially better paths. MCTS loses its effectiveness when there are many repetitions of the algorithm. Therefore, exploitation comes into the picture to balance out the exploration strategy.  Exploitation stays on only a single route with the highest assessed value. This is a greedy strategy that will increase the depth rather than the width of the tree. The UCB formula helps explore the relatively unexplored nodes of the tree and finds possibly more optimal paths than the currently known paths. Thus, it balance outs the exploration-exploitation trade-off.

Monte Carlo Tree Search Algorithm

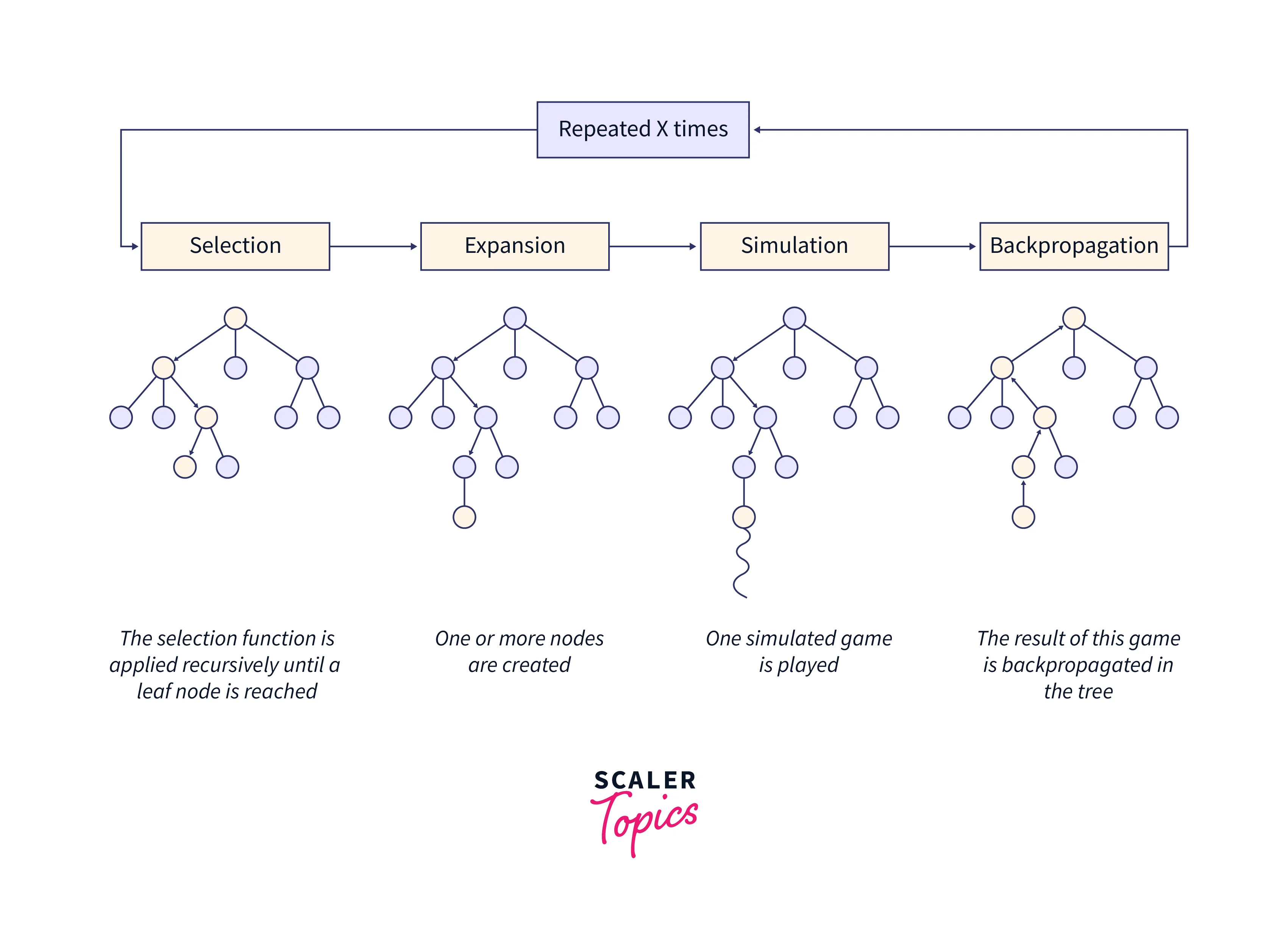
The Monte Carlo Tree Search (MCTS) technique is used to solve decision-making issues, particularly in games. It is based on a Monte Carlo simulation, which estimates the predicted results of various actions by randomly selecting game states. Each node in the search tree created by the MCTS algorithm represents a state of the game. The method then iteratively completes the following four steps:

Selection

The MCTS algorithm performs this phase by iteratively traversing the current tree starting at the root node. An evaluation function is used to choose nodes with the highest estimated value in the best way possible. MCTS uses the Upper Confidence Bound (UCB) formula applied to trees for optimal selection. It balances the trade-off between exploration and exploitation. A node that returns the maximum value (based on some input parameters) is chosen during tree traversal. The MCTS enters the expansion step during traversal once a child node that is also a leaf node is discovered. The formula that is frequently used for this purpose is shown below.

Parameters:

• Si = value of a node i
• xi = empirical mean of a node i
• C = constant value
• t = total number of simulations

Expansion

In this step, a new child node is added to that node where the selection process has reached optimally.

Simulation

In this phase, a simulation is run by selecting actions or strategies until a predetermined state is reached.

Backpropagation

The remaining tree must be modified after figuring out the value of the newly inserted node. The backpropagation process is carried out to backpropagate from the new node to the root node. The number of simulations kept in each node increases throughout the backpropagation process. Moreover, the number of wins is increased if the simulation performed by the new node produces a win.

Implementation of Monte Carlo Tree Search

The following is the implementation of the Monte Carlo Search algorithm:

Output:

Now, let us a line-by-line explanation of the above code.

This code defines a class for a node in the search tree. Each node has a state (represented by an object of some state class), a parent node (except for the root node), a list of child nodes, and two variables used for backpropagation: visits (the number of times the node has been visited) and wins (the number of times the node has led to a win).

This code checks if all legal moves from the current node have been explored and returns True if all moves have been explored, otherwise False.

This code checks if the current node represents a terminal state, that is, a state where the game is over and no more moves can be made.

This code returns the child node with the highest win rate. This is used for selecting the next node to explore.

This code expands the current node by creating child nodes for all legal moves that have not yet been explored. Each child node is created by applying a legal move to the current state and creating a new MCTSNode object with the resulting state.

This code simulates a game from the current state by randomly selecting moves until a terminal state is reached. The winner of the game is returned.

This code updates the node's visit count and wins count based on the result of the simulated game.

This code calculates the UCT (Upper Confidence bound applied to Trees) score for the node. The UCT score balances the exploration and exploitation of the search tree by taking into account the number of times a node has been visited and the average win rate of its child nodes.

Advantages of MCTS

Monte Carlo Tree Search (MCTS) is a popular algorithm for decision-making and game-playing tasks. Some of the advantages of using MCTS include the following:

• Strong performance: MCTS performs well in various game-playing tasks, including chess, go, and poker.
• Minimal domain knowledge: MCTS requires only minimal knowledge of its working domain. With minimal expertise, it can solve many tasks without needing external task-specific heuristics.
• Adaptable: MCTS can adapt to environmental changes using simulations. These simulations can be used to explore new states of the environment.
• Robustness: Because it takes a probabilistic approach to decision-making and can deal with environmental uncertainty, MCTS is resilient to noisy or incomplete information.
• Scalability: MCTS can carefully explore the most promising regions of the search space, allowing it to scale to vast and complex decision-making tasks.
• Exploration-exploitation balance: MCTS balances the trade-off between exploration and exploitation, enabling it to discover new and optimal strategies while exploiting promising options.

MCTS is a sophisticated algorithm that can be used for various gaming and decision-making tasks, offering outstanding performance and flexibility with little domain expertise.

Disadvantages of MCTS

Monte Carlo Tree Search (MCTS), while its benefits, has a few drawbacks as well that should be taken into account:

• Computationally Intensive: The time and space complexity of the MCTS algorithm depend on various factors, such as the size of the game tree, the number of simulations per move, and the branching factor of the tree. However, in general, the time complexity of MCTS is exponential in the depth of the game tree and linear in the number of simulations per move. The space complexity is also proportional to the size of the game tree. Thus, simulating a large number of game states using MCTS can be computationally intensive. Therefore, it makes it challenging to apply MCTS to tasks that require fast decision-making.
• Requires a Large Number of Simulations: MCTS algorithm can be time-consuming and computationally expensive. This is because it requires many simulations to achieve a stable performance state.
• Bias Towards Early Moves: MCTS may be biased in favor of early moves in the search tree as these states are investigated more frequently and have more information available about them.
• Can Be Vulnerable to Specific Strategies: In certain games, MCTS can be exposed to particular strategies or techniques that are challenging to foresee or resist.
• Lack of Human Intuition: Human intuition and knowledge can be useful in some decision-making tasks. But MCTS lacks the incorporation of human intelligence.
• Difficult to Tune: Because the algorithm's performance can be susceptible to selecting parameters and heuristics, MCTS can be challenging to tweak and optimize.

Overall, MCTS is a strong algorithm with many benefits. Still, it has several drawbacks and difficulties that must be carefully considered for particular tasks or domains.