Asymptotic Notations

Asymptotic notations in data structure are mathematical tools used to analyze the runtime of algorithms as input size grows. They enable comparison of algorithm efficiencies without manual runtime calculations, particularly beneficial for larger inputs. This article delves into different types of asymptotic notations and their application, excluding discussions on space complexity. Asymptotic notations offer crucial insights into algorithm performance, aiding in algorithm selection and optimization.

What is an Asymptotic Notation?

Asymptotic notation is a mathematical notation that is used to analyze the time complexity and the runtime of an algorithm for a large input.

For example if we want to compare the runtimes of the bubble sort algorithm and merge sort algorithm, we can use asymptotic notations to do this comparison.

In this article, we will discuss three types of asymptotic notations that are most commonly used to analyze time complexities of various algorithms. These are Big O notation (O), omega notation (Ω) and theta notation (θ).

Big O Notation (Represented as O)

Let $f(n)$ and $g(n)$ be two functions dependent on the input variable n. So, the function $f(n)=O(g(n))$ if there exists some positive constants $c$ and $n^{\prime }$ such that f(n) <= c.g(n) for all $n>=n^{\prime }$.

For example, let f(n) = 2n + 5.

In order to find the Big O of this function, we have to find another function $g(n)$ such that f(n) <= c.g(n) for all $n>=n^{\prime }$ where $c$ and $n^{\prime }$ are positive constants.

If we take $g(n)=7n$ and put this is the above equation, we can see that $(2n+3)<=(7n)$ for all $n>0$ and $c=7$. Hence, we can say that the function $f(n)=O(7n)$. But we write it as $f(n)=O(n)$ as we generally analyze an algorithm for a large input $n$ and if $n$ is large, $n$ is approximately equal to $7n$.

The comparison of the function $f(n)$ and $g(n)$ can also be seen in the graph given below. The function $f(n)<=g(n)$ for points where $n>x$.

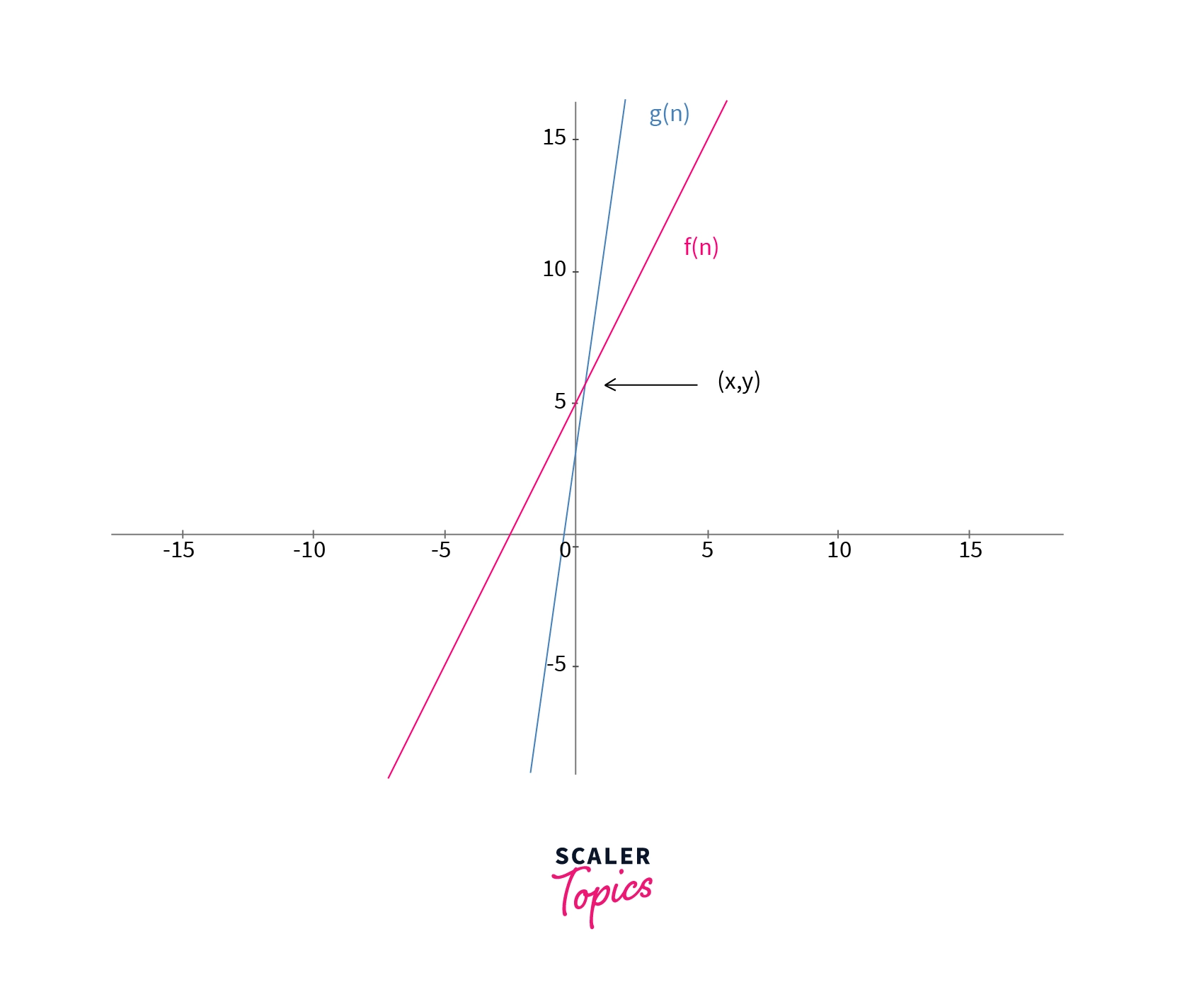
Let us now take the example f(n) = 7(n^2) + 3.

If we take a function $g(n)=10(n^2)$, we can see that it satisfy the equation given for Big O notation with $c=10$ and $n^{\prime }=1$. So, we can say that the function $f(n)=O(10n^2)$ which can be approximately written as $f(n)=O(n^2)$ since we are considering it only for large values of $n$.

The Big O notation is also called as upper bound notation. For example for the above example, we can say that the upper bound of the function $f(n)=7(n^2)+3$ is $n^2$.
:::
:::section{.tip}
NOTE:

For the example f(n) = 7(n^2) + 3, one may also determine the function $g(n)$ as $g(n)=(n^3)$ since it satisfies all the conditions of Big O notation. Although $O(n^3)$ is the right answer for this function, we generally find the function which is closest to $f(n)$ and satisfying the condition of Big O notation. So the most suitable answer is $O(n^2)$.

Omega Notation (Represented as Ω)

Let $f(n)$ and $g(n)$ be two functions dependent on the input variable $n$. So, the function f(n) = Ω(g(n)) if there exists some positive constants $c$ and $n^{\prime }$ such that f(n) >= c.g(n) for all $n>=n^{\prime }$.

For example, let f(n) = 2n + 5.

In order to find the omega of this function, we have to find another function $g(n)$ such that f(n) >= c.g(n) for all $n>=n^{\prime }$ where $c$ and $n^{\prime }$ are positive constants.

If we take $g(n)=7n$ and put this is the above equation, we can see that $(2n+3)>=(1.n)$ for all n >= 0 and c = 1. Hence, we can say that the function $f(n)=\Omega (n)$.

The comparison of the function $f(n)$ and $g(n)$ can also be seen in the graph given below. The function $f(n)>=g(n)$ for points where n > x.

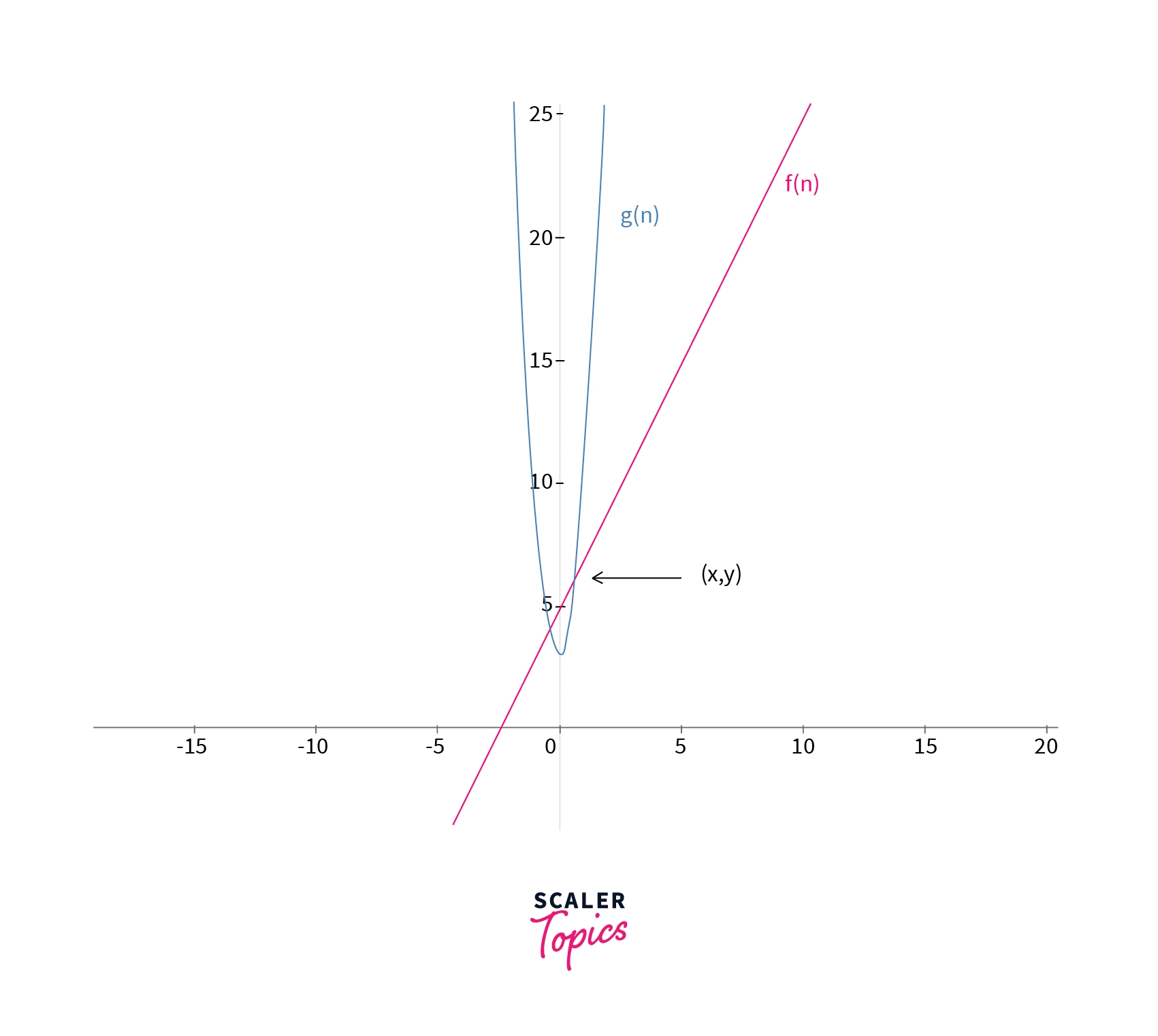
Let us now take the example f(n) = 7(n^2) + 3.

If we take a function $g(n)=1.(n^2)$, we can see that it satisfy the equation given for omega notation with c = 1 and n' = 0. So, we can say that the function $f(n)=\Omega (n^2)$.

The omega notation is also called as lower bound notation. For example for the above example, we can say that the lower bound of the function $f(n)=7(n^2)+3$ is $n^2$.

NOTE:

For the example $f(n)=7(n^2)+3$, one may also determine the function $g(n)$ as $g(n)=((1/2).(n^2))$ since it satisfies all the conditions of omega notation. Although $O((1/2).(n^2))$ is the right answer for this function, we generally find the function which is closest to $f(n)$ and satisfying the condition of omega notation. So the most suitable answer is $\Omega (n^2)$.

Theta Notation (Represented as θ)

Let $f(n)$ and $g(n)$ be two functions dependent on the input variable n. So, the function f(n) = θ(g(n)) if there exists some positive constants $c1,c2$ and $n^{\prime }$ such that $c1.g(n)<=f(n)<=c2.g(n)$ for all $n>=n^{\prime }$.

For example, let f(n) = 2n + 5.

In order to find the theta of this function, we have to find another function $g(n)$ such that $c1.g(n)<=f(n)<=c2.g(n)$ for all $n>=n^{\prime }$ where $c1,c2$ and $n^{\prime }$ are positive constants.

If we take $g(n)=n,c1=1$ and $c2=5$ and put this is the above equation, we can see that $(1.n)<=(2n+3)<=(5.n)$ for all $n>=0,c1=1$ and $c2=5$. Hence, we can say that the function $f(n)=\theta (n)$.

The comparison of the function $f(n)$, $c1.g(n)$ and $c2.g(n)$ can also be seen in the graph given below. The function $f(n)>=c1.g(n)$ and $f(n)<=c2.g(n)$ for points where $n>x$.

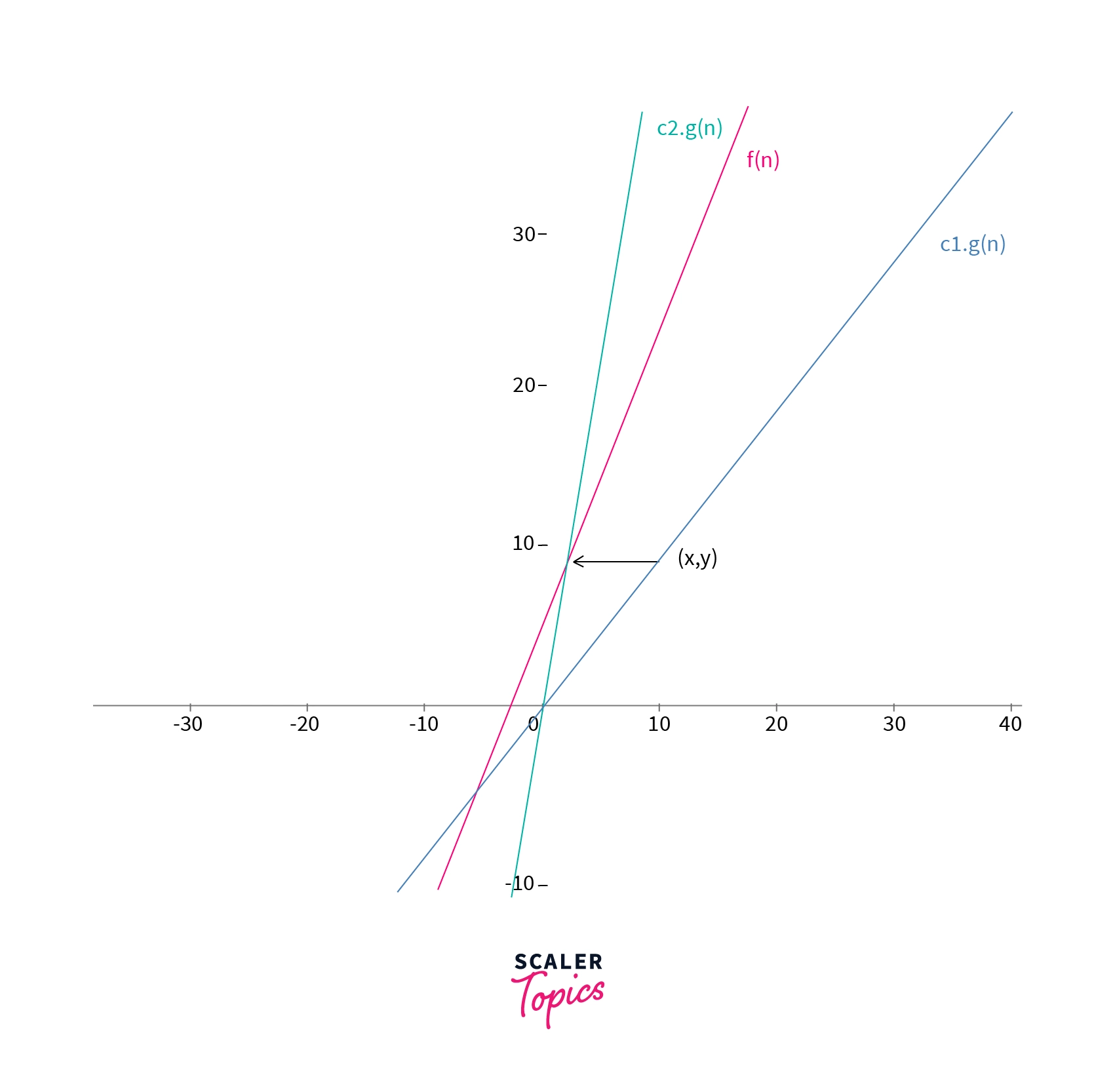
The theta notation is also called as tight bound notation. For example for the above example, we can say that the tight bound of the function $f(n)=2n+5$ is $n$.

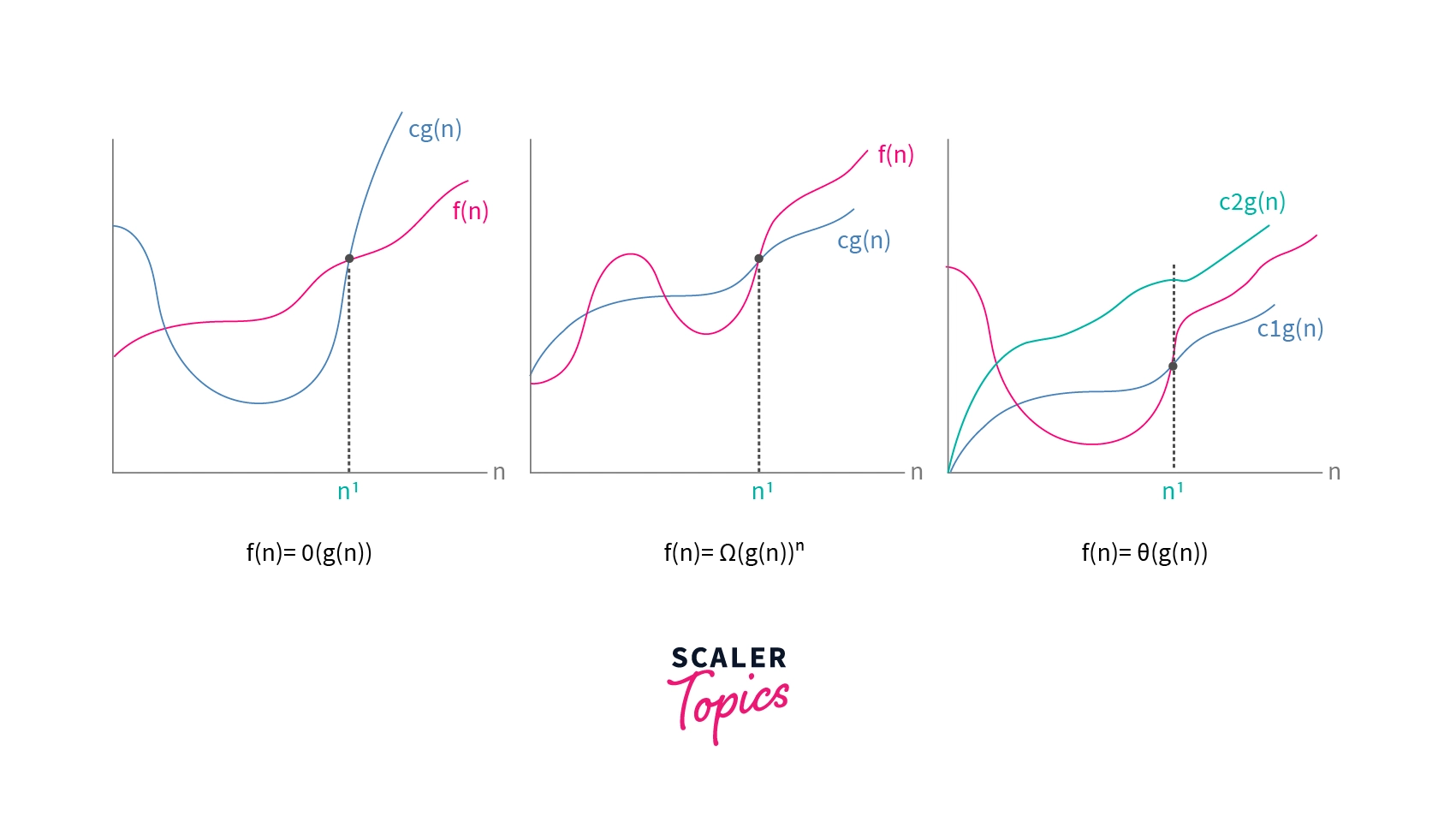
Graphical Representation for the Asymptotic Notations

Below are the graphical plots to represent the three asymptotic function (i.e. Big O notation, Omega notation and Theta notation) with respect to the input variable $n^{\prime }$.

Properties of Asymptotic Notation

Here are some properties that are satisfied by the asymptotic notations that are discussed above. All these properties can be easily proved by applying the equation we discussed in each asymptotic notation’s section.

General

If we have two functions $f(n)$ and $g(n)$ such that f(n) = O(g(n)), then for a constant $c$, $c.f(n)$ is also $O(g(n))$.

Similarly,

If f(n) = Ω(g(n)), then c.f(n) = Ω(g(n)).
If f(n) = θ(g(n)), then c.f(n) = θ(g(n)).

Multiplying a constant scaler with the function will not affect any of the equations that we saw while discussing each asymptotic notation.

Transitive

If we have three functions $f(n),g(n)$ and $h(n)$ such that f(n) = O(g(n)) and g(n) = O(h(n)), then f(n) = O(h(n)).

For example, if we have a function $f(n)=n$, $g(n)=n^2$ and $h(n)=n^3$.

• Since $f(n)<=g(n)$, we can say $f(n)=O(g(n))$.
• Also, $g(n)<=h(n)$, this means that $g(n)=O(h(n))$.

Now, if $f(n)=O(g(n))$ and $g(n)=O(h(n))$, we can conclude $f(n)<=g(n)<=h(n)$. This means that $f(n)<=h(n)$.

Hence, we can can say that $f(n)=O(h(n))$.

Similarly,

If $f(n)=\Omega (g(n))$ and $g(n)=\Omega (h(n))$, then $f(n)=\Omega (h(n))$.
If $f(n)=\theta (g(n))$ and $g(n)=\theta (h(n))$, then $f(n)=\theta (h(n))$.

We can verify this property using the equations that we have discussed in the section of each asymptotic notation.

Reflexive

If we have a function f(n), then by default, we can write,

$f(n)=O(f(n))$,

$f(n)=\Omega (f(n))$,

$f(n)=\theta (f(n))$.

We can verify this property using the equations that we have discussed in the section of each asymptotic notation.

Symmetric

If we have two functions $f(n)$ and $g(n)$ such that f(n) = θ(g(n)), then we can also say that g(n) = θ(f(n)).

We can verify this property using the equation that we have discussed in the section of theta notation.

NOTE: This property only satisfies for theta $(\theta )$ notation.

Transpose

If we have two functions $f(n)$ and $g(n)$ such that f(n) = O(g(n)), then we can say that $g(n)=\Omega (f(n))$.

We can verify this property using the equations that we have discussed in the section of each asymptotic notation.

NOTE: This property only satisfies for Big O $(O)$ and Omega $(\Omega )$ notations.

Conclusion

• Asymptotic notations in data structure are indispensable tools for understanding the efficiency of algorithms as input size grows.
• They enable straightforward comparison of algorithm efficiencies without the need for manual runtime calculations, especially beneficial for large inputs.
• The three primary types discussed here include Big O, Omega, and Theta notations, each offering unique insights into algorithm performance.
• Asymptotic notations are widely used in algorithm analysis and design, aiding in algorithm selection and optimization strategies.
• Various properties such as transitivity, reflexivity, symmetry, and transposed symmetry further enhance the utility and applicability of asymptotic notations in algorithm analysis.