What is the Base Address of a Two Dimensional Array?

Introduction

A two-dimensional array is an array of arrays. This means that each element of the two-dimensional array is also an array, thus making a matrix-like structure called a two-dimensional array in C++.

It is a multidimensional array. Two-dimensional arrays are represented as array_name[n][m], where n is the number of rows and m is the number of columns.

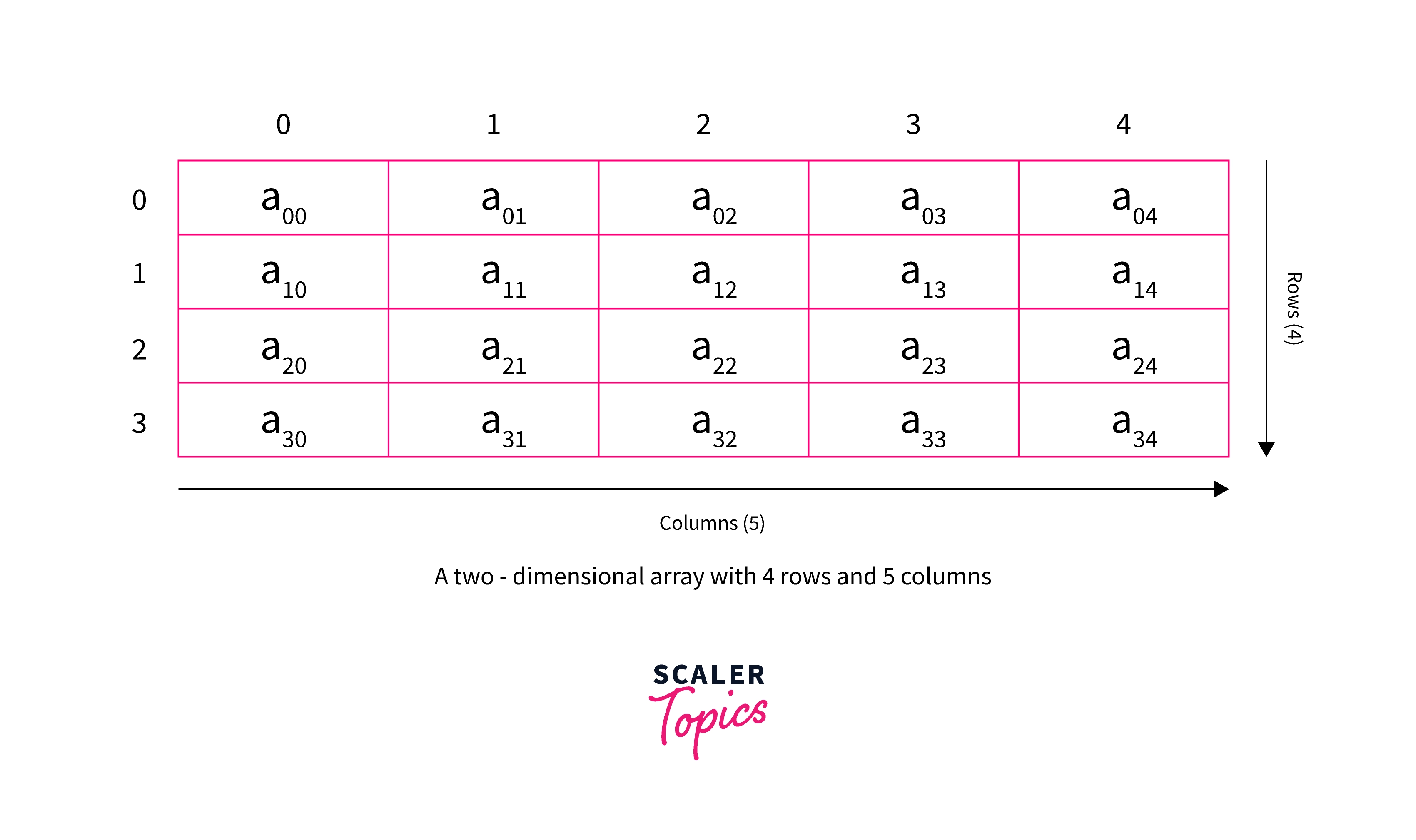
In this article, we will explore the base address of such a two-dimensional array and how we can calculate the address of any element in such an array in C++. Before moving on to this, let us recall the base address for a one-dimensional array in C++.

The base address of a two-dimensional array or an array is a reference starting point, using which the addresses of all the array elements can be calculated. These addresses that are calculated using the base address are called absolute addresses. In the case of a one-dimensional array, the base address points to the location of the first element of the array. In the case of a two-dimensional array, the base address points to the first element of the first row of the 2-d array, i.e., array_name[0][0].

How can we calculate the absolute address of any array element if we know its base address? An array is stored in a contiguous manner in the memory. So if we know the base address, which is the location from where array storage starts in memory, then we need to know the index of the element whose address is to be found. The size of memory each element takes up, and we can easily find out the absolute address of any element.

This process is simple enough for a one-dimensional array. But what happens in the case of a two-dimensional array?

In the next section, let us learn how to calculate the element address in a two-dimensional array.

Calculating the Address of any Element in Two Dimensional Arrays

To be able to understand the process of calculating the absolute address for elements of a two-dimensional array, it is important to know how a two-dimensional array is stored in memory.

Even though a two-dimensional array looks very distinct from a one-dimensional array in C++, the way they are stored in memory is not very different. The two-dimensional structure of a 2-d array is for the user's convenience to provide a matrix-like structure. These two-dimensional arrays are stored like one-dimensional arrays in the memory.

So, to store a 2-d array in memory, we need to map the elements into a 1-d array, and then they are stored in a contiguous manner in the memory for easy access.

This mapping and consequent memory storage can be achieved using two techniques:

• Row Major Order
• Column Major Order

Let us look at both of these in detail.

Row major order

In this kind of order, as the name suggests, rows are ordered contiguously in memory one after the other. This means that first, all the elements of the first row are stored in memory, followed by all elements of the second row, and so on.

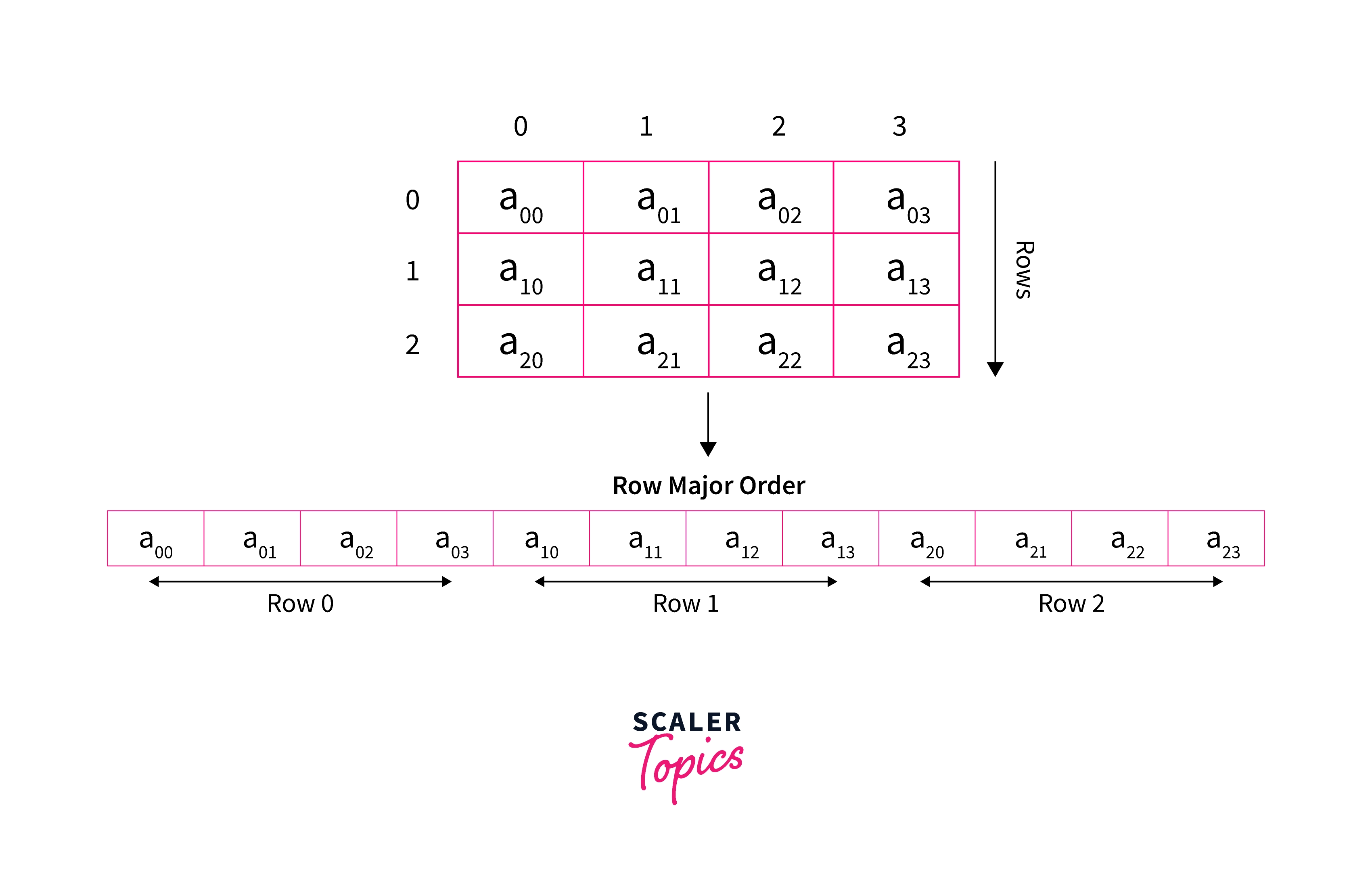
Hence, we have a one-dimensional array from a two-dimensional array where rows are stored contiguously. The address for any element array_name[i][j], where i denotes the row number, and j denotes the column number(0-based index) of the element, in such an ordering will be:

Now as the elements are ordered in a row-major order, the number of elements between arr[i][j] and the first element of the array will be equal to the number of rows before the row in which this element resides * the number of elements in one row + index of the element in its row.

This is nothing but (i * m + j) for the element arr[i][j], where m is the number of columns in the array.

Hence, the absolute address of any element in row-major ordering becomes:

For example, consider the above image. If we need to find out the absolute memory address of a[1][2] in row-major ordering.

In this case, i = 1, j = 2 and m = 4. Applying everything to the formula, we get,

If we compare from the image, the element a[1][2] does occur after 6 elements when it is converted into a one-dimensional array using row-major ordering.

Column Major Order

In this kind of order, as the name suggests, columns are ordered contiguously in memory one after the other. This means that all the elements of the first column are stored in memory, followed by all elements of the second column, and so on.

Hence, we have a one-dimensional array from a two-dimensional array where columns are stored contiguously. The address for any element array_name[i][j], where i denotes the row number, and j denotes the column number(0-based index) of the element, in such an ordering will be:

Now, as the elements are ordered in column-major order, the number of elements between arr[i][j] and the first element of the array will be equal to the "number of columns before the column in which this element resides * number of elements in one column + row number of the element" (as this will be the number of elements stored in this column before this element in column-major order)

This is nothing but (j * n + i) for the element arr[i][j] where n is the number of rows in the array.

Hence, the absolute address of any element in row-major ordering becomes:

For example, consider the above image. If we again need to find out the absolute memory address of a[1][2] in column-major ordering.

In this case, i = 1, j = 2, and n = 3. Applying everything to the formula, we get,

If we compare from the image, the element a[1][2] does occur after 7 elements when it is converted into a one-dimensional array using column-major ordering.

Pointer to a 2D Array

Just like we can have pointers to one-dimensional arrays in C++, we can also have pointers to two-dimensional arrays. The syntax for declaring a pointer to two-dimensional arrays in C++ is:

Here, data_type refers to the data type of the two-dimensional array, n is the number of rows, and m is the number of columns in the two-dimensional array. This pointer can now store the base address of the two-dimensional array in C++.

How to Pass Two-Dimensional Arrays to a Function?

In this part, we will learn how to provide a 2D array to any function and access its elements.

In the following code, we send the array to a function print_arr(), which output the supplied 2D array.

Output

In the above code, we pass an array arr with the number of rows and columns to specify the size of the array. We use row and column values to print all the array elements in the function print_arr().

How to Pass Two Dimensional Arrays as a Single Pointer to a Function?

We can also pass the array with a single pointer to the function. In the following code, we send the array to a function show_arr(), which output the supplied 2D array.

Output

In the above code, we pass a pointer to an array arr with the number of rows and columns to specify the size of the array. We use row and column values to print all the array elements in the function show_arr().

How to Pass Two Dimensional Arrays as a Double Pointer to a Function?

We can also pass the array in terms of double pointer to the function. In the following code, we send the array to a function show_arr(), which outputs the supplied 2D array.

Output

In the above code, we pass a pointer to an array arr with the number of rows and columns to specify the size of the array. We use row and column values to print all the array elements in the function show_arr().