BCNF in DBMS
FREE
BCNF (Boyce-Codd Normal Form) in DBMS, introduced by R.F. Boyce and E.F. Codd in the 1970s, is a normalization technique that eliminates table redundancy and anomalies for enhanced data integrity. While 2NF and 3NF address certain dependencies, BCNF addresses additional constraints that can persist, causing redundancy even in 3NF relations. Despite 3NF's adequacy, BCNF offers a more robust solution by specifically addressing cases where 3NF falls short in eliminating 100% redundancy due to certain functional dependencies.
What is BCNF in DBMS?
BCNF (Boyce Codd Normal Form) stands for Boyce-Codd Normal Form and is an advanced level of database normalization, often also called the 3.5 Normal Form. In other words, codd normal form bcnf is a stricter stage beyond 3NF in which the form bcnf in dbms is used to improve data integrity.
3NF doesn’t remove 100% redundancy in the cases where for a functional dependency (say, A->B), A is not the candidate key of the table. To deal with such situations, BCNF was introduced to reduce redundancy, support eliminating redundancy, keep minimal redundancy, and prevent anomalies when 3NF still leaves problematic dependencies.
BCNF is based on functional dependencies, and all the candidate keys of the relation are taken into consideration. BCNF is stricter than 3NF and has some additional constraints along with the general definition of 3NF.
A table or relation is said to be in BCNF in DBMS if the table or the relation is already in 3NF, and also, for every functional dependency (let’s say, X->Y), X is either the super key or the candidate key. In simple terms, for any case (let’s say, X->Y), X can’t be a non-prime attribute.
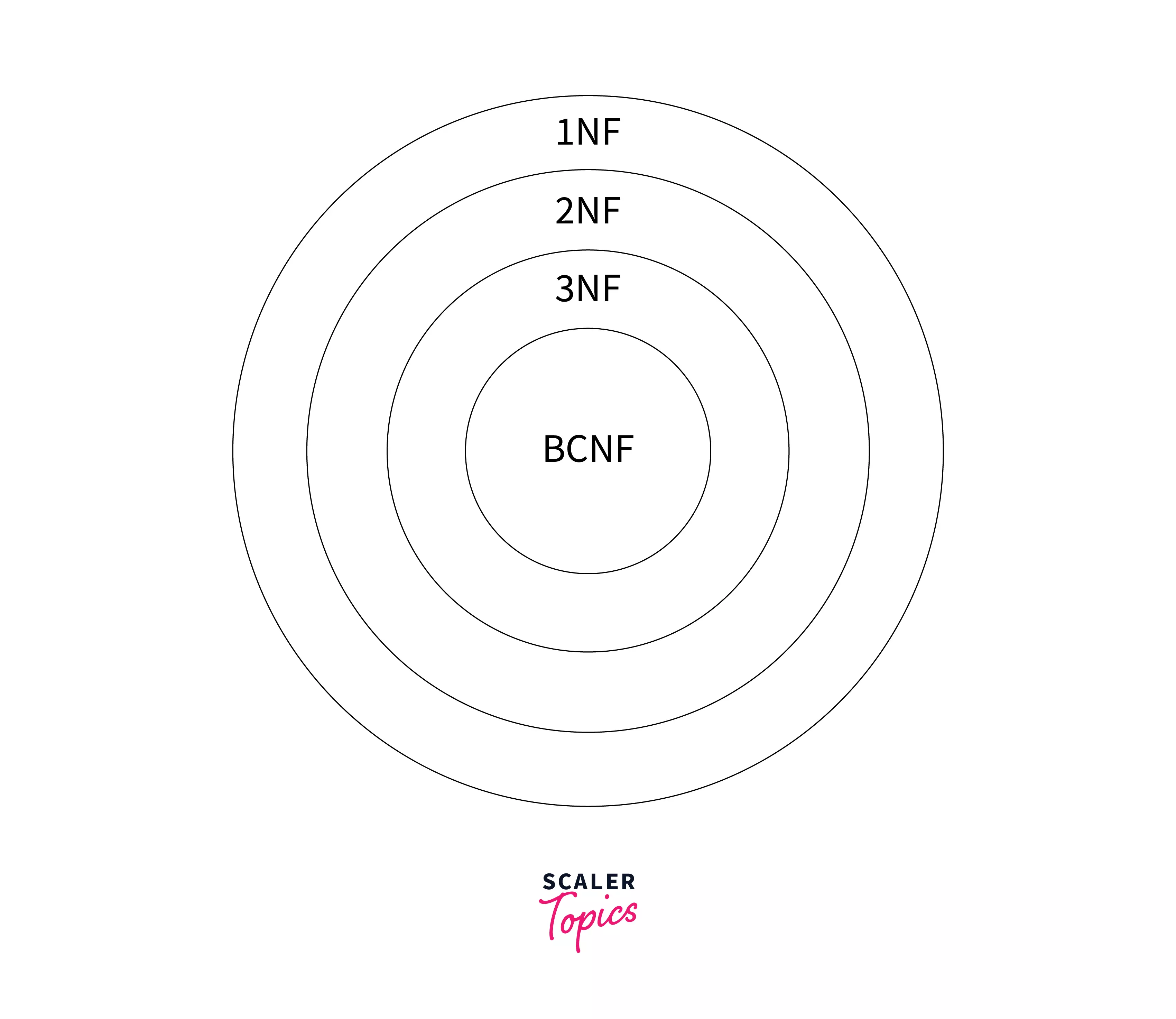
To find the highest normalization form of any relation R with functional dependencies, we first need to check whether the relation is in BCNF or not. If relation R is found to be in BCNF, it simply means that the relation R is also in 3NF, 2NF, and 1NF as the hierarchy shown in the above image.
Similarly, if the relation is found to be in 3NF, it is also in 2NF and 1NF. The 3NF in DBMS has more restrictions and strict constraints than the first two normal forms, but it is less strict than the BCNF. This shows that the restriction always increases as we traverse down the hierarchy.
Rules for BCNF and Functional Dependencies in DBMS
A table or relation is said to be in BCNF (Boyce Codd Normal Form) if it satisfies the following two conditions, the following rules that we have already studied in its definition:
-
It should satisfy all the conditions of the Third Normal Form (3NF).
-
For every non trivial functional dependency, the determinant on the left hand side must be a super key or candidate key, which are stricter conditions than 3NF. In simple words, if a functional dependency exists among the following attributes, A can’t be a non-prime attribute when B is a prime attribute.
Examples
Transform Your Career
Choose from our industry-leading programs designed for career success
Modern Software and AI Engineering Program
Master full-stack development with AI integration
+1000 moreModern Data Science and ML with specialisation in AI
Advanced data science techniques with AI specialization
+1000 moreAdvanced AIML with Specialisation in Agentic AI
Deep dive into AIML with focus on Agentic systems
+1000 moreDevOps, Cloud & AI Platform Engineering
Build and manage AI-powered cloud infrastructure
+1000 moreAI Engineering Advanced Certification by IIT-Roorkee
Premier AI engineering certification from IIT-Roorkee
Example 1:
In this example, we have to find the highest normalization form, and for that, we are given a relation R(A, B, C, D, E) with functional dependencies as follows: { BC->D, AC->BE, B->E }
-
As we can see, (AC)+={A, C, B, E, D} and also, none of its subsets can determine all the attributes of the relation. There is another point to be noted that A or C can't be derived from any other attribute of the relation, and therefore, there is only one candidate key,{AC}.
-
Prime attributes in DBMS are always part of the candidate keys, and for this relation R, prime attributes are: {A, C} while non-prime attributes are: {B, E, D}.
-
Clearly, there is no multi-valued attribute in the relation R, and hence, it is at least in 1NF.
-
BC->D is in 2NF because BC is not a proper subset of the candidate key AC. AC->BE is also in 2NF because AC itself is a candidate key, and lastly, B->E is again in 2NF. For 2NF, there must not be any partial dependency present in the table, and hence, relation R here is in 2NF.
-
The relation R is not in 3NF because BC->D at the start is not in 3NF (BC is not a candidate key, and also, D is not a prime attribute). Hence, the relation R has 2NF as the highest normalization form.
Example 2:
In this example, we have to again find the highest normalization form, and for that, we are given a relation R(A, B, C) with functional dependencies as follows: {AB ->C, C ->B, AB ->B} Candidate Key (given): {AB}
-
Clearly, prime attributes for Relation R are: {A,B} while non-prime attributes are: {C}.
-
For this particular example, let us start from the order of hierarchy with higher restrictions, and firstly, we will check for BCNF here.
-
Clearly, {AB->C} and {AB->B} are in BCNF because AB is the candidate key present on the LHS of both dependencies. The second dependency, {C->B}, however, is not in BCNF because C is neither a super key nor a candidate key. This functional dependency violates BCNF because a non-key attribute functionally determines a key attribute, so the table violates BCNF.
-
C->B is, however, present in 3NF because B is a prime attribute that satisfies the conditions of 3NF. Hence, relation R has 3NF as the highest normalization form, while BCNF is a stronger version of 3NF that resolves anomalies 3NF can still allow, including those from overlapping composite candidate keys.
Example 3:
In this example, we have a relation R with three columns: Id, Subject, and Professor. We have to find the highest normalization form, and also, if it is not in BCNF, we have to decompose it to satisfy the conditions of BCNF.
| Id | Subject | Professor |
|---|---|---|
| 101 | Java | Mayank |
| 101 | C++ | Kartik |
| 102 | Java | Sarthak |
| 103 | C# | Lakshay |
| 104 | Java | Mayank |
Interpreting the table:
-
One student can enroll in more than one subject.
-
Example: student with Id 101 has enrolled in Java and C++.
-
A professor is assigned to the student for a specified subject, and when the same course appears in multiple rows, repeated professor assignments can introduce redundancy.
Finding the solution:
-
Using Id and Subject together, we can find all unique records and also the other columns of the table. Hence, the Id and Subject together form the primary key.
-
The table is in 1NF because all the values inside a column are atomic and of the same domain.
-
We can’t uniquely identify a record solely with the help of either the Id or the Subject name. As there is no partial dependency, the table is also in 2NF.
-
There is no transitive dependency because the non-prime attribute i.e., Professor, is not deriving any other non-prime attribute column in the table. Hence, the table is also in 3NF.
-
There is a point to be noted that the table is not in BCNF (Boyce-Codd Normal Form).
Why is the table not in BCNF?
As we know each professor teaches only one subject, but one subject may be taught by multiple professors. This means one subject can appear in multiple rows, and the redundancy caused by the dependency between subject and professor becomes visible. In the same way that Instructor depends on CourseID in a StudentCourse table, here Professor depends on Subject, and Subject is not a super key. As we know the professor column is a non-prime attribute, while the subject is a prime attribute. This violates BCNF because the determinant on the left hand side of the dependency is not a super key. For BCNF, the deriving attribute (professor here) must be a prime attribute.
Turn Learning into Career Growth
How to satisfy BCNF?
In Example 3, to achieve bcnf, we decompose the relation into multiple tables: the Student table and the Professor table, which is how we apply bcnf. This decomposition eliminates redundancy, improves database design, enhances performance during updates, minimizes storage space, and can reduce the need for complex validation triggers. The trade offs are that achieving BCNF can increase the number of tables and joins, may weaken dependency preservation because some functional dependencies can be lost and checked only across tables, and in practice some systems do not fully apply bcnf and keep 3NF instead.
Student Table and Candidate Keys
| P_Id | S_Id | Professor |
|---|---|---|
| 1 | 101 | Mayank |
| 2 | 101 | Kartik |
| 3 | 102 | Sarthak |
| 4 | 103 | Lakshay |
| 5 | 104 | Mayank |
Professor Table
| Professor | Subject |
|---|---|
| Mayank | Java |
| Kartik | C++ |
| Sarthak | Java |
| Lakshay | C# |
| Mayank | Java |
Here, Professor determines Subject in this decomposed table, so the non-trivial dependency has a determinant that works as a key for the relation. Storing the original relation as two tables also keeps each fact in one place and helps reduce redundancy. Hence, it is in BCNF.
Example 4:
Let's take another general example to understand the concept of decomposition in detail, though higher normal forms may still be considered after BCNF for more complex cases: We have a relation R(A, B, C, D) that is already in 3NF. Candidate Keys: {A, BC} Prime Attributes: {A, B, C} Non-Prime Attributes: {D}
Functional dependencies are as follows: {A->BCD, BC->AD, D->B}
The above relation is not in BCNF because {D->B} is not in BCNF as {D} is neither a candidate key nor a prime attribute. Hence, we will decompose the relation R into R1{A, D, C} and R2{D, B}. Similarly, a ProjectAssignment table violates BCNF because ProjectManager depends on ProjectID, which is not a superkey. After BCNF, fourth normal form handles multivalued dependencies.
Conclusion
-
BCNF (Boyce Codd Normal Form) is an advanced level of database normalization, a stronger version of the third normal form (3NF), and is often also known as the 3.5 Normal Form.
-
A relation is said to be in BCNF in DBMS if the relation is already in 3NF and, for every non trivial functional dependency (say, X->Y), X must be a super key or candidate key on the left hand side.
-
If ant relation R is found to be in BCNF, it simply means that the relation R is also in 3NF, 2NF, and 1NF.
-
The 3NF in DBMS has more restrictions and strict constraints than the first two normal forms, but it is less strict than the BCNF.
-
This shows that the restriction always increases as we traverse down the hierarchy.
-
BCNF can improve data integrity and reduce anomalies, but there are trade-offs, such as more joins and weaker dependency preservation after decomposition.
Read More:
Google
Amazon
Microsoft
Flipkart
Adobe1200+ more