Bias and Variance in Machine Learning

Bias and variance are two critical concepts in machine learning that influence the performance and generalization of models. Understanding the balance between bias and variance is essential for building models that accurately capture the underlying patterns in data while avoiding overfitting or underfitting.

What is Bias?

In machine learning, bias refers to the error introduced when a model oversimplifies the underlying patterns in the data. It arises from assumptions made by the model that may not accurately represent the complexities of the real-world problem. Bias can be represented as the expected difference between the predicted output of the model and the true output:

$\text{Bias} = E[\hat{f}(x) - f(x)]$

Where:

• $\hat{f}(x)$ represents the predicted output of the model for input ( x ).
• $f(x)$ represents the true output for input $x$.
• $E[\cdot]$ denotes the expected value operator.

A high-bias model tends to oversimplify the data and may fail to capture important patterns, leading to underfitting. Underfitting occurs when the model performs poorly on both the training and test data because it is too simplistic to accurately represent the underlying relationships.

How to Reduce High Bias in Machine Learning?

Reducing bias in machine learning models involves making them more complex or flexible so they can capture the underlying patterns in the data more accurately.

1. Increase Model Complexity:
   One approach to reduce bias is to increase the complexity of the model. This can be done by adding more features or increasing the capacity of the model.

2. Use Sophisticated Algorithms:
   Some machine learning algorithms are inherently more complex and can capture complex relationships in the data better than others.

3. Gather More Data:
   Increasing the amount of data available for training can provide the model with a richer representation of the underlying patterns.

4. Perform Feature Engineering:
   Feature engineering involves creating new features or transforming existing ones to make them more informative for the model which helps reduce bias.

What is Variance?

Variance in machine learning refers to the variability of model predictions for a given input. It quantifies how much the predictions of a model fluctuate when trained on different subsets of the training data. A high variance model tends to produce significantly different predictions for slightly different training datasets, indicating that it is capturing noise rather than the underlying patterns in the data.

Mathematically, variance can be expressed as the expected squared difference between the predicted output of the model and its mean prediction:

$\text{Variance} = E[(\hat{f}(x) - E[\hat{f}(x)])^2]$

Where:

• $\hat{f}(x)$ represents the predicted output of the model for input $x$.
• $E[\hat{f}(x)]$ represents the expected value (mean prediction) of the model's output for input ( x ).
• $E[\cdot]$ denotes the expected value operator.

How to Reduce High Variance in Machine Learning?

Reducing high variance in machine learning models involves making them more robust and less sensitive to fluctuations in the training data.

1. Simplify the Model:
   One approach to reduce variance is to simplify the model by reducing its complexity or the number of features. This can help prevent the model from fitting the noise in the training data and focus on capturing the underlying patterns.

2. Regularisation:
   Regularisation techniques add penalties to the loss function to discourage the model from fitting the training data too closely. Common regularization techniques include L1 regularization (lasso) and L2 regularisation (ridge), which add a penalty term to the loss function based on the magnitude of the model parameters.

3. Cross-Validation:
   Cross-validation is a technique used to assess the performance of a model and select the best-performing model. By splitting the training data into multiple subsets (folds) and training the model on different combinations of these subsets, cross-validation provides a more reliable estimate of the model's performance and helps identify models that generalize well to unseen data.

4. Gather More Training Data:
   Increasing the size of the training data can help provide the model with a more stable representation of the underlying patterns in the data. More training data reduces the influence of random fluctuations and helps the model learn more robust patterns.

Total Error Mathematical Derivation

The decomposition of the total error of a machine learning model into bias squared, variance, and irreducible error provides valuable insights into the sources of error in the model's predictions.

Mathematical Proof:

Let's start with the definition of the total error (TE) of a machine learning model:

$\text{Total ~Error} = E[(Y - \hat{f}(x))^2]$

Where:

• $Y$ represents the true output.
• $\hat{f}(x)$ represents the predicted output of the model for input ( x ).
• $E[\cdot]$ denotes the expected value operator.

Using this definition, we can express the total error as follows:

$\text{Total Error} = E[(Y - E[\hat{f}(x)] + E[\hat{f}(x)] - \hat{f}(x))^2]$

Expanding the square and rearranging terms, we get:

$\text{Total~ Error} = E[(Y - E[\hat{f}(x)])^2 + 2(Y - E[\hat{f}(x)])(E[\hat{f}(x)] - \hat{f}(x)) + (E[\hat{f}(x)] - \hat{f}(x))^2]$

Now, let's consider each term individually:

1. Bias Term:

$\text{Bias}^2 = (E[\hat{f}(x)] - Y)^2$

This represents the squared difference between the expected value of the model's predictions and the true output, averaged over all possible training datasets.

2. Variance Term:

$\text{Variance} = E[(\hat{f}(x) - E[\hat{f}(x)])^2]$

This represents the expected squared deviation of the model's predictions from their mean, averaged over all possible training datasets.

3. Irreducible Error:

$\text{Irreducible~ Error} = E[(Y - E[Y])^2]$

This represents the squared difference between the true output and its expected value, which any model cannot reduce, as it is inherent to the data itself.

Now, if we substitute these terms back into the original equation for total error, we get:

$\text{Total~ Error} = \text{Bias}^2 + \text{Variance} + \text{Irreducible~ Error}$

Bias-Variance Combinations

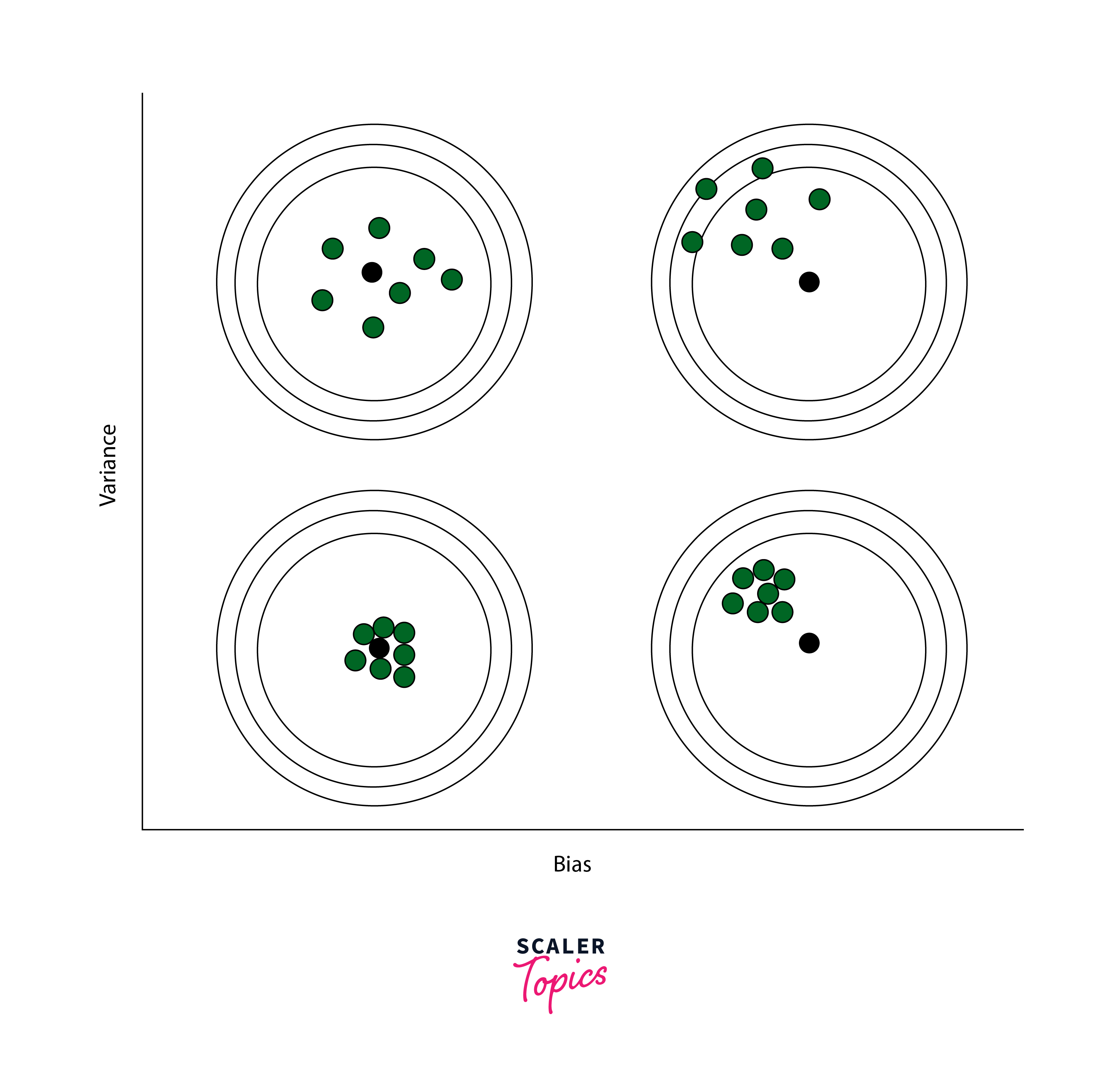
In machine learning, the relationship between bias and variance is crucial for understanding the behavior of models and achieving optimal performance.

1. High Bias and Low Variance:
   Models with high bias and low variance tend to oversimplify the underlying patterns in the data. These models are often too rigid and fail to capture the complexity of the data. As a result, they underfit the data, meaning they perform poorly both on the training set and on unseen data. High-bias models may overlook important relationships in the data, leading to suboptimal predictive performance.
2. Low Bias and High Variance:
   On the other hand, models with low bias and high variance are highly flexible and can capture complex patterns in the training data. However, they are also more sensitive to noise and fluctuations in the data, leading to overfitting. Overfitting occurs when the model learns to fit the training data too closely, capturing noise rather than true underlying patterns. As a result, these models tend to have poor generalization performance, meaning they do not perform well on unseen data.
3. High Bias and High Variance:
   In some cases, machine learning models may exhibit both high bias and high variance simultaneously, indicating a complex interaction between model simplicity and sensitivity to training data fluctuations. These models are overly simplistic to capture the data's underlying patterns while also being excessively influenced by noise, leading to poor performance on both training and test datasets.
4. Ideal Balance - Low Bias and Low Variance:
   The goal in machine learning is to find the ideal balance between bias and variance. This balance involves building models that accurately capture the underlying patterns in the data without being too simplistic (high bias) or too complex (high variance). Models with low bias and low variance generalize well to unseen data and have optimal predictive performance.

Bias-Variance Tradeoff

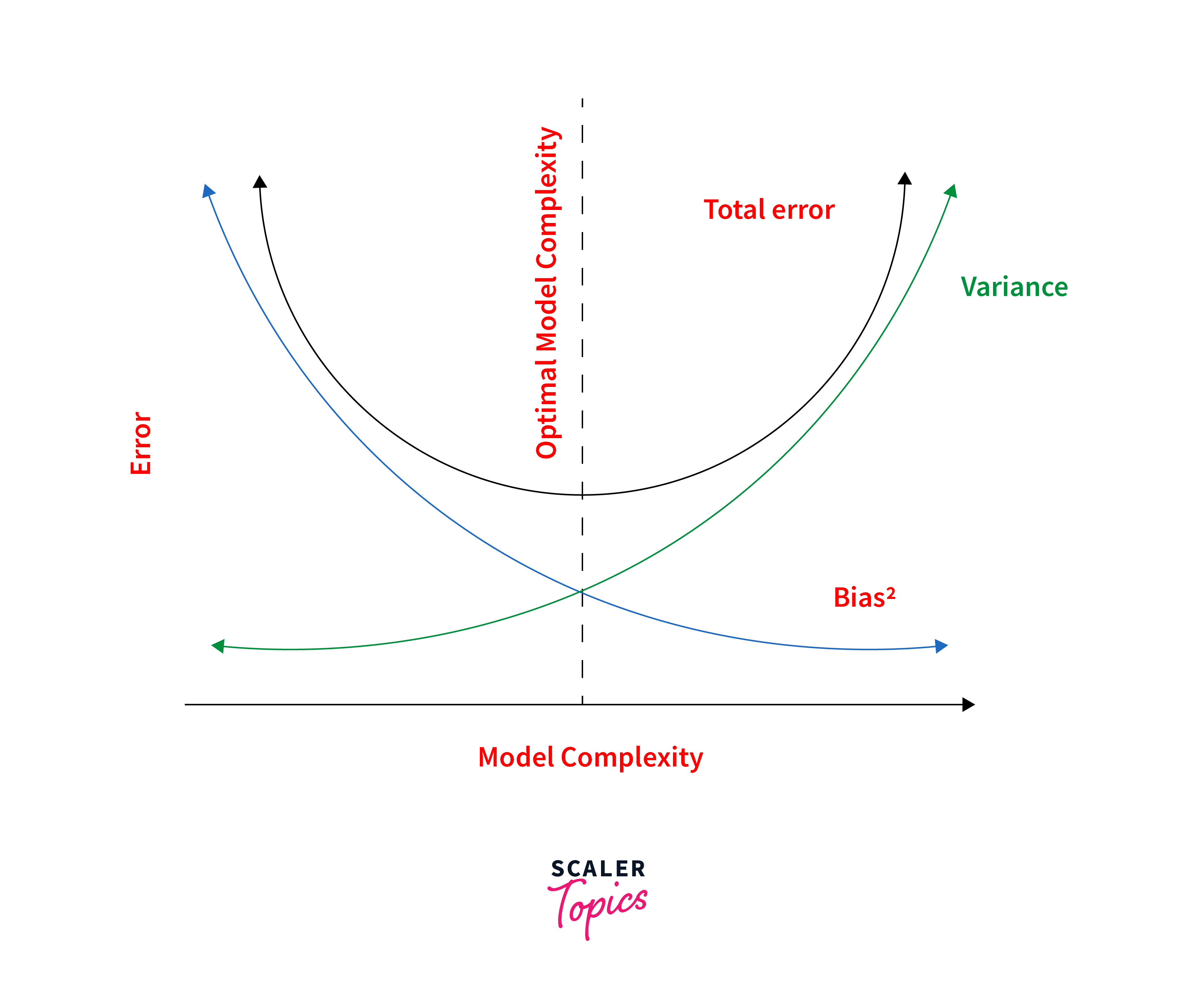
The bias-variance tradeoff in machine learning represents the balance between bias and variance in model performance. Understanding this tradeoff is crucial for developing models that generalize well to unseen data while avoiding underfitting and overfitting. The trade-off arises because decreasing bias often increases variance, and vice versa.

Decomposition of Bias-Variance for Regression and Classification

In regression, the bias-variance decomposition can be expressed as:

• $Bias^2 = E[(f̂ - f)^2]$
• $Variance = E[(f̂ - E[f̂])^2]$
• $Total~Error = Bias^2 + Variance + Irreducible Error$

In classification, a similar decomposition can be applied, where bias and variance are calculated based on the misclassification rate or other appropriate metrics.

Regression Example:

Output for Regression Example:

Classification Example:

Output for Classification Example: