C Program for Binary Search (Data Structure)

Binary Search

Binary Search in C is generally used to solve a wide range of issues in computer science and real-world scenarios related to searching.

We have many search algorithms like Linear Search or Sequential Search, Binary Search, Jump Search, Fibonacci Search, etc. and one of the most efficient is the Binary Search algorithm.

In linear search, we compare each element with the target from the start to the end of an array with time complexity of O(n) , while the binary search takes only O(log N) time, we will see how.

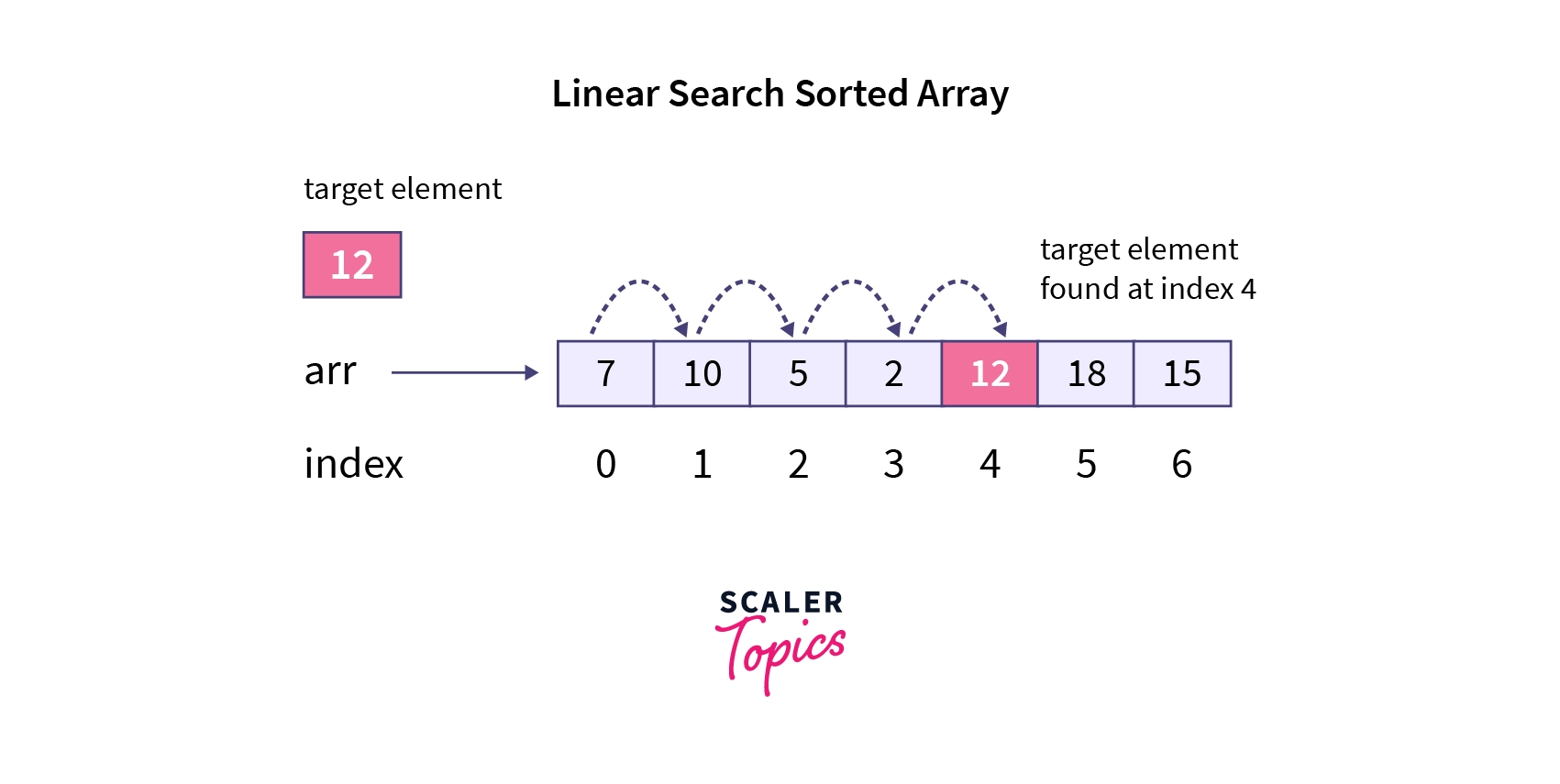
Binary search algorithm operates on a sorted array to find a target element and it is more efficient than the linear search algorithm. So, let's see how does binary search algorithm work.

Conditions for when to apply Binary Search in a Data Structure

To use the Binary Search algorithm effectively, the following conditions must be met:

1. The data structure must be sorted.
2. Access to any element of the data structure takes constant time.

Binary Search Algorithm

1. Initialization:

   • Set left to the index of the first element in the search space.
   • Set right to the index of the last element in the search space.

2. Search:

   • Calculate the middle index mid as (left + right) / 2.
   • Compare the element at index mid with the target key.
   • If the key is found at mid, the search is successful, and the process terminates.
   • If the key is not found at mid, proceed to the next step.

3. Choose Search Space:

   • If the element at index mid is smaller than the target key, narrow down the search space to the right half by setting left to mid + 1.
   • If the element at index mid is larger than the target key, narrow down the search space to the left half by setting right to mid - 1.

4. Repeat:

   • Repeat steps 2 and 3 while left is less than or equal to right.
   • If the key is found, return mid.

5. Termination:

   • If left becomes greater than right, then the target key is not in the dataset, and the search process concludes.

How does Binary Search work?

In binary search, we reduce the search space in half at each iteration, find the mid index, and compare the middle element with the target element. If the target element is bigger than the middle element, we reduce the array to the right half only, beginning with the mid + 1 (just next to mid) index. If the target element is smaller than the middle element, we reduce the array to the left half only, ending before the mid - 1 index (just before the mid).

Now suppose, we are provided with a sorted array and a target element (let's say k) and we want to search if k exists in the array or not, and if k does exist in the array, we return the index/position of k in the array.

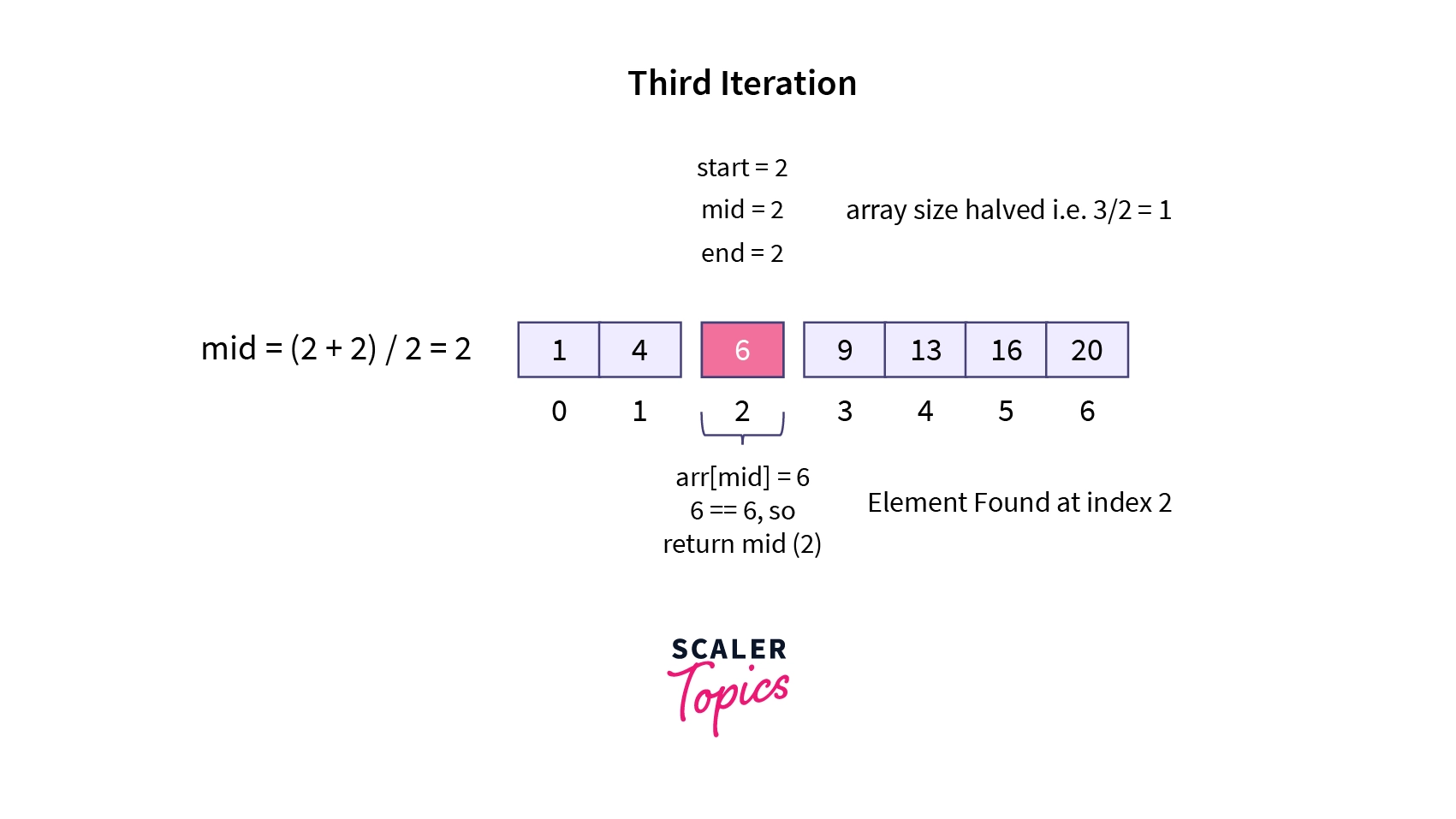
So, let's consider a sorted array shown in the image below and try to search number 6 and return its index. Please note the array has a total of 7 elements.

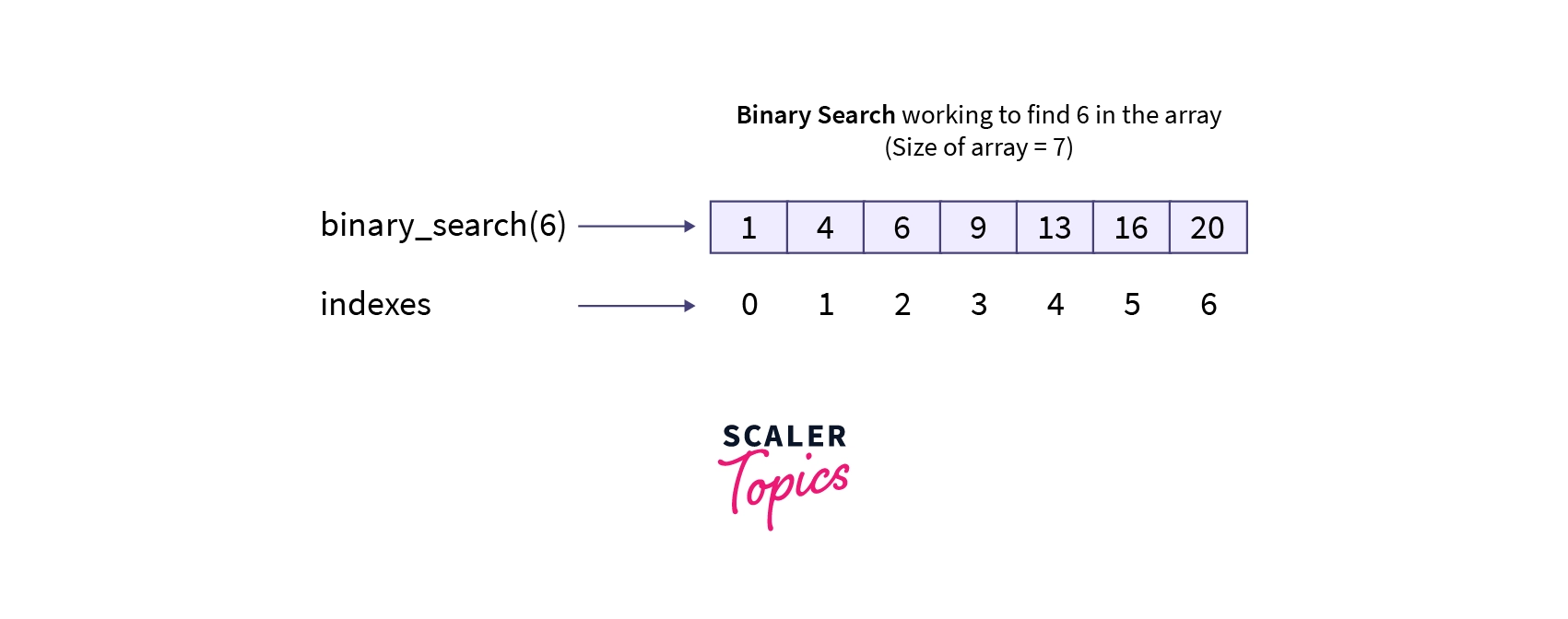
• First, Let's initialize some variables:

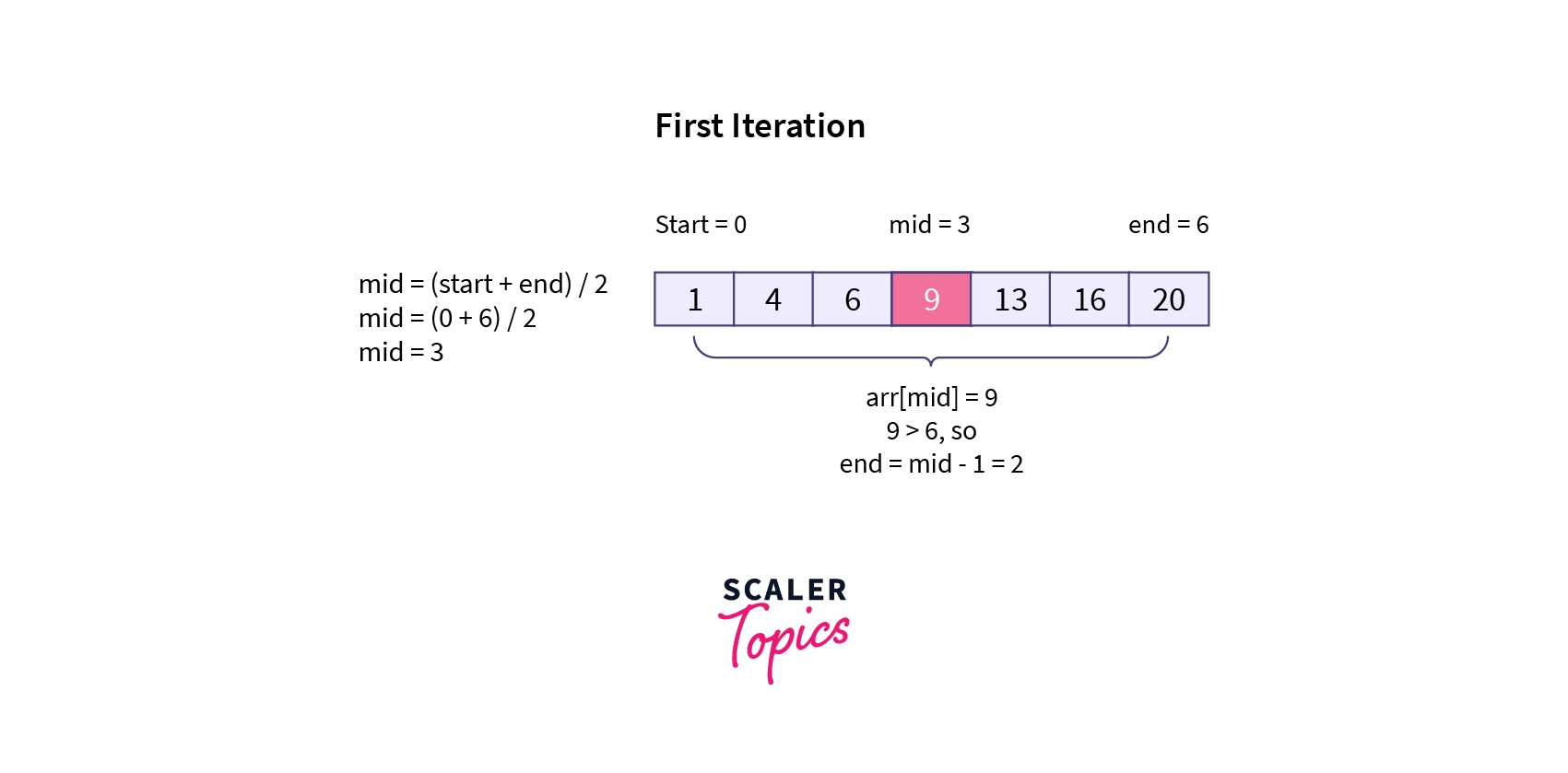
• In the first iteration of binary search, we check if the middle element is equal to 6. If it is equal, we return the mid index. Here, arr[mid] = arr[3] = 9, i.e., not equal to 6. So, we check if the middle element is greater than or less than 6. Now, 9 is greater than 6, so we assign mid - 1 (= 2) index to the end variable that reduces the array size by half (we know that 6 will be present on the left side of the array, as we are working in a sorted array).

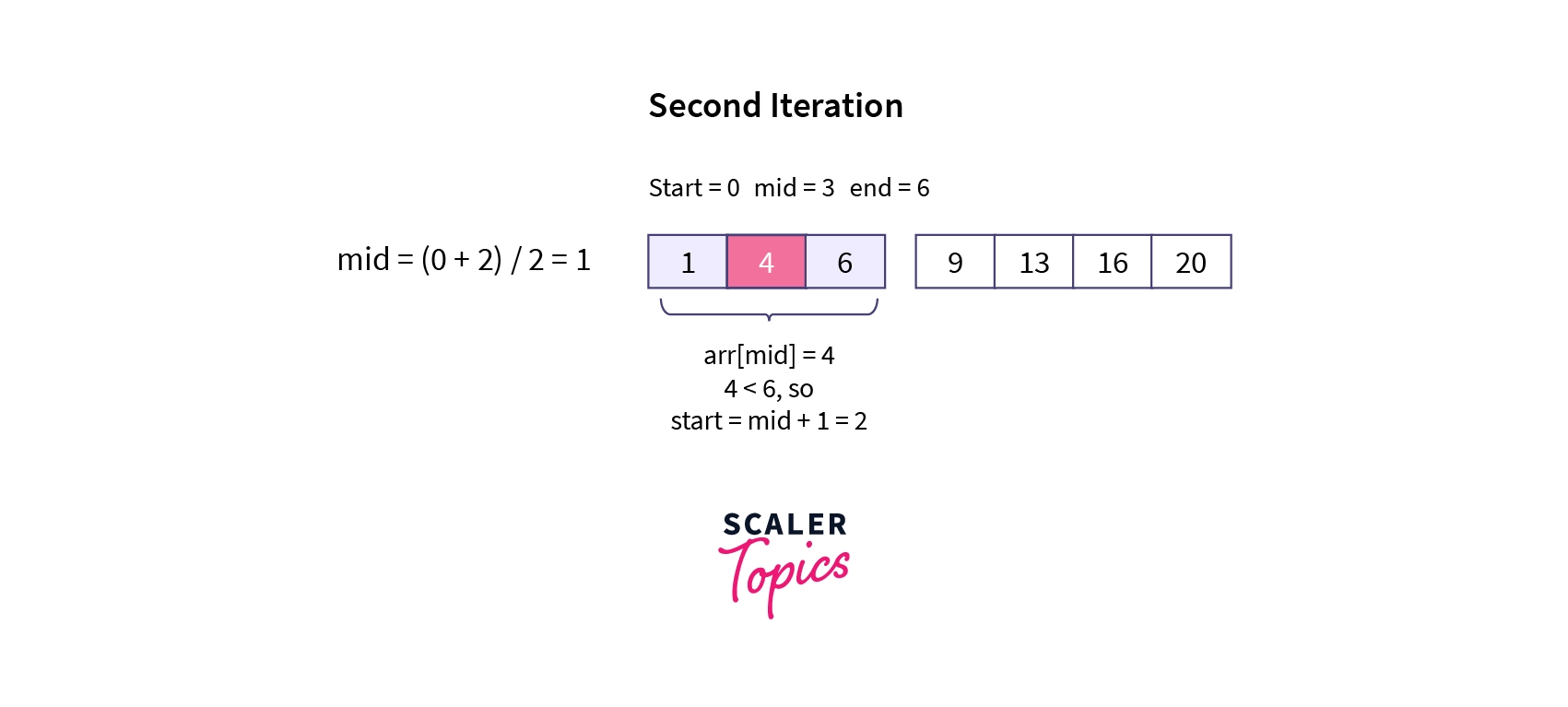
• In the second iteration, again, we check if the middle element is equal to, greater than, or smaller than 6. Now, the middle element 4 is greater than 6, so we assign mid + 1 index to the start variable.

• In the third iteration, the middle element equals 6, so we return the mid index value, i.e., 2.

You can relate the working of binary search with an example of a Dictionary. Suppose our task is to find the meaning of the word tranquil. In a dictionary, words are arranged in alphabetical order.

One approach would be to read and compare each word in the dictionary with the target word (linear search). However, as you might have noticed, this method is time-consuming as you have to scan the entire dictionary.

Is there a better approach? Yes, we can use the binary search as described above.

We can open the middle page in the dictionary and compare the words on the middle page with tranquil. If the word tranquil comes after the words on the middle page in alphabetical order, we will disregard the right side portion of the dictionary. Otherwise, we will ignore the left side portion of the dictionary.

We continue this process until we find the word tranquil. Now, we know tranquil means a state of peace.

How to Implement Binary Search?

The Binary Search Algorithm can be implemented in the following two ways

1. Iterative Binary Search Algorithm
2. Recursive Binary Search Algorithm

Iterative Binary Search Algorithm

Binary Search in C using iterative is similar to the recursion method. We are using the while() loop to imitate the recursion.

• First, let's initialize some variables:
  • start = 0 (index of first element in the array),
  • end = size - 1 (index of last element in the array),
• While the start index is smaller than equal to the end index, we keep searching for the element.
• Calculate mid = start + ((end - start) / 2), index of the middle element in the array at each iteration inside the loop.
• If the search element (k) is equal to the middle element, return the mid index value.
• If the search element (k) is smaller than the middle element, we assign mid - 1 to the end variable.
• If k is greater than the middle element, we assign mid + 1 to the start variable.
• If the element is not found, i.e., the start becomes greater than the end, we exit the while loop and return -1, i.e., element not found.

Let's see the program for binary search in C using the iterative method.

C Program :

Check and run this program using InterviewBit IDE.

Custom Input:

Output:

Custom Input:

Output:

Explanation :

• We have taken input from the user (the element to be searched) and stored it in the data variable.
• We have called the binary_search() method, with arr, 7 (size of the array), and data (search element) as arguments.
• Lastly, we have printed the returned index value of the data element if it is in the array else printed -1.

Recursive Binary Search Algorithm

Recursive Binary Search uses binary_search() function repeatedly calls itself with simplified arguments of array indexes until a base condition is reached, at some specified conditions discussed below:

• If the search element (k) is smaller than the middle element, we call the binary_search(a, start, mid - 1, k) method with the end as mid - 1.
• If the search element (k) is greater than the middle element, we call the binary_search(a, mid + 1, end, k) method with the start as mid + 1.
• There are two exit conditions for this recursion:
  1. If the search element is not found, return -1, i.e., start becomes greater than the end.
  2. If the element is found return the mid index.

Now let's see the program for binary search in C using recursion.

C Program :

Check and run this program using InterviewBit IDE.

Custom Input:

Output:

Custom Input:

Output:

Explanation :

• We have taken input from the user (the element to be searched) and stored it in the data variable.
• We have called the binary_search() method, with arr, 0 (start index of the array), 6 (end index of the array), and data (search element) as arguments.
• Lastly, we have printed the returned index value of the data element, if it is in the array else printed -1.

For example, in competitive programming questions, various test cases have very large values for the number of elements in an array (for example, 2126753390). So, if we use the mid = (start + end) / 2, at some point, (start + end) will cross the INT_MAX value (i.e., +2147483647), which will give an integer overflow error as follows:

Suppose, start index is 1063376696, while end index is 2126753390. In this case, if we use mid = (start + end)/2 expression, it will cause an integer overflow error.

But, if we use mid = start + (end - start) / 2); (end - start) will avoid the integer overflow to occur (it will not cross the INT_MAX value) and this is why we use this expression to calculate our middle index, to fulfill all the test cases compatibility in a programming question.

Now, let's see the implementation of binary search in C language using the iterative method.

Complexity Analysis of Binary Search

The time complexity of binary search algorithm is:

• O(1) in the best case.
• O(log N) in the worst case.

Time complexity describes the amount of time the algorithm takes on input provided.

Best Case: The best case is when the target element is present in the middle of the list. Binary search always begins its search with the middle element. It makes no difference whether the list comprises five or one million elements. Therefore, the best case time complexity of the binary search for a list of size N is O(1), i.e., independent of the size of the input N.

Worst Case: The worst-case scenario is that the target element is not present in the list. The time taken to search the target element in the list is determined by the number of times we need to halve the list until we reach the final element. Therefore, the worst-case time complexity of the binary search for a list of size N is O(log N).

An algorithm is O(log N) if it takes a constant time to cut the problem size by a fraction (usually by 1/2). Let's look at this mathematically:

In binary search, Length of the array: N (at iteration 1)
After iteration 1: N / 2 (size of the array is decreased by 1/2 after each iteration)
After iteration 2: (N / 2) / 2 = N / 4 = N / 2²
After iteration 3: (N / 4) / 2 = N / 8 = N / 2³
. . Suppose after k iterations array size becomes 1, so
After iteration k: N / 2^k = 1

Therefore, N = 2^k

Taking log₂ both sides,

⇒ log₂(N) = log₂(2^k)

Since, log(x^y) = y * log(x)

⇒ log₂(N) = k * log₂(2)

Since, log_a(a) = 1

⇒ log₂(N) = k * 1

or,

⇒ k = log₂(N)

This proves that the time complexity of the binary search algorithm is O(log N).

The space complexity of binary search algorithm:

• O(1) in the case of the iterative method.
• O(log N) in the case of the recursive method.

Space complexity illustrates memory usage(RAM) while executing the program with more significant inputs. Our program never needs additional memory in the most typical implementation of the binary search (i.e., iterative binary search). We would search the target element in the array during every iteration by updating the start and end index. Therefore, the size of our input does not affect the additional space required for the binary search algorithm, and the space complexity is constant O(1), i.e., space complexity is independent of input N (size of the array).

Advantages of Binary Search

• It is efficient because it continually divides the search space in half until it finds the element or only one element remains in the list to be tested.
• It specifies whether the element being searched is before or after the current place in the list.
• It is the fastest searching algorithm with the worst-case time complexity of O(log N) and works best for large lists.

Drawbacks of Binary Search

• The list/array must be sorted before applying the binary search algorithm. For example, with lists where elements are added constantly it is difficult to make the list remain sorted.
• It is a little more complicated as compared to linear search in searching an element from the list.
• It is not that efficient as compared to other searching algorithms for smaller list/array sizes.

Applications of Binary Search

1. Foundational Element in Machine Learning: Binary search serves as a fundamental component in machine learning algorithms, enabling tasks like neural network training and the determination of optimal hyperparameters.

2. Utilized in Computer Graphics: Within the realm of computer graphics, Binary Search plays a pivotal role in tasks such as ray tracing and texture mapping, aiding in the efficient retrieval of graphical information.

3. Database Search Operations: Binary search is widely employed for searching and retrieving data within databases, enhancing the speed and precision of query operations.