Binary Search in C++

Binary search in C++ is a searching algorithm that returns the position of the key( element to be searched) in a sorted array. In every consecutive step, it compares the middle element of the array with the key. If they are unequal, the algorithm searches on the left or right subarray depending on whether the key is lesser or greater than the middle element.

The time complexity of the Binary Search in C++ is $O(log(n))$ and the space complexity of the Binary Search in C++ is $O(1)$.

Algorithm of the Binary Search in C++

The steps to perform a Binary search in C++ are as follows.

• Start with the whole interval of the array.
• If the value of the search key is equal to the middle element of the interval, return this index.
• If the search key's value is less than the middle element of the interval, narrow the interval to the left subarray.
• If the value of the search key is greater than the middle element of the interval, narrow the interval to the right subarray.
• Repeat until the search key is found or the interval becomes empty.

The time complexity of Binary search c++ code is $O(log(N))$ where N is the size of the array. This is because we reduce the length of the search interval by half every time. The space complexity is $O(1)$.

Illustration of Binary Search Algorithm

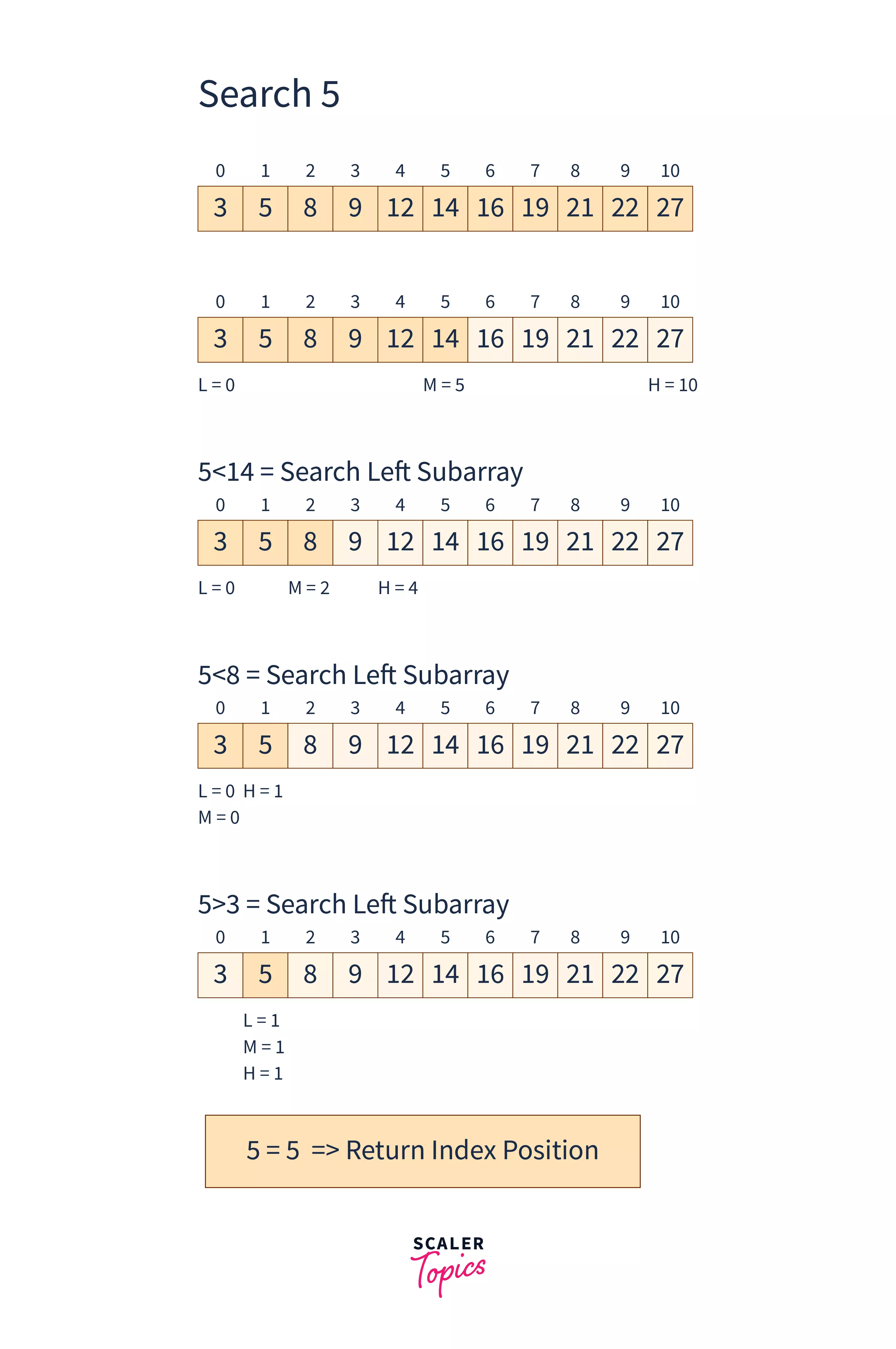
Steps to Perform the Binary Search

To perform a binary search in C++ on a sorted array, follow these steps. Let's take an example of a sorted array A = [1, 3, 5, 7, 9, 12], and we want to search for the value 5.

1. Initialize: Set two pointers, low at the start of the array (0) and high at the end (5 in this case for the array size minus one).
2. Calculate the Midpoint: Find the mid-index, mid = low + (high - low) / 2. Initially, mid = 0 + (5 - 0) / 2 = 2.5, which we round down to 2.
3. Compare the Target: Check if the target value (5) is equal to the value at mid (A[mid] = 5). If they match, you've found the target, and the search ends.
4. Adjust the Search Range: If the target is less than A[mid], narrow the search to the left half by setting high = mid - 1. Otherwise, search the right half by setting low = mid + 1.
5. Repeat or Conclude: Continue steps 2 through 4 until the value is found or the low exceeds high, indicating the value isn't in the array.

Recursive Implementation of Binary Search

In this method, we call the Binary search C++ function for the complete array then the function will check the middle element of the array; if it is equal to the key, the search is over, and if not, then the function will make a recursive call to the binary search C++ function again either for the left sub-array or right sub-array.

The recursive implementation of the Binary search program in C++ is as follows.

Output :

Explanation:

We create a function rBinarySearch taking four parameters - array, the lower and upper index of the array, and x, the number we want to search in our array. The input array must be sorted in order. So if x is not equal to the element present at the index mid, it may be either on the left or the right. We continue our search by calling the function again until we get an index where x is present; in that case, we will return that index. Else, the element is not present in the array, and we return -1.

Time Complexity : $O(log(n))$

At each step of the function, we reduce our search space by half. So the number of steps required to reach the base case is $log(n)$. Also, at each step, we perform constant or $O(1)$ operations. So the time complexity of the recursive method is $O(log(n))$ $*$ $O(1)$ = $O(log(n))$.

Proof:

• First Iteration : Length of array = $n$
• Second Iteration : Length of array = $n/2$
• Third Iteration : Length of array = $n/(2^2)$ and so on.

Let's say the length of the array becomes one after k iterations. Then

• $n/(2^k) = 1$
• $n=2^k$
• $log(n)=log(2^k)$ {log both side}
• $k*log(2) = log_2(n)$
• $k=log_2(n)/log(2)$
• $k=log_2(n)$ {approx.}

Space Complexity : $O(log(n))$

A recursive function creates a call stack whose size depends on the number of times the function is called. In the worst case, the function can be called $(log(n)+1)$ times. Therefore, the space complexity of the recursive method is $O(log(n))$.

Iterative Implementation of Binary Search

In this method, we implement Binary search C++ code iteratively. lo represent the starting index of the selected sub-array, and hi represent the ending index of the selected sub-array. We will start with lo as 0 and hi as (array size-1) to cover the whole array.

While loop will check in every iteration if middle element is equal to the key or not and update the lo and hi accordingly to proceed to the next sub-array if the key is not found. The iterative implementation of Binary search program in C++ is as follows.

Output :

Explanation:

We create a function iBinarySearch taking four parameters - array, the lower and upper index of the array, and x, the number we want to search in our array. The input array is already sorted. So if x is not equal to the element present at the index mid, it may be either on the left or the right. So we narrow our search to either the left subarray or the right subarray. We return this index if we get an index where x is present. Else, the element is not present in the array, and the function returns -1.

Time Complexity : $O(log(n))$

Space Complexity : $O(1)$

All operations are performed on the array, and no extra space is created. Therefore, the space complexity of the iterative method is $O(1)$.