Binary Search in JavaScript

Overview
Binary search is a search algorithm that is designed to search an element in a sorted array. This binary search is also a well-known example of the "divide and conquer approach".
Now we will further study more about binary search in javascript in this article.
Introduction to Binary Search in JavaScript
Nowadays, in the domain of computer science, searching for an element is one of the most frequently used tasks. So due to this frequently used of such things, we have to make it more efficient, for which there are lots of data structures and algorithms exist.
So Binary Search here is also one of the efficient algorithms which are used in searching an element, but a matter of fact here is that the array should be sorted before applying the binary search over it. Binary search is one of the most widely used search algorithms, and it can be used in almost any real-world application.
Binary search works in a divide and conquers way. It divides the array into two halves and performs the searching of the required target value on those halves instead of searching an element on each index, like on index 0 first, then on 1st index, and so on.
Binary Search is a simple, user-friendly, and efficient search algorithm. The only fact is that this algorithm only works with sorted arrays, so we may require to sort our array before performing the binary search on an array.
Now let's understand the implementation of binary search in javascript.
Implementation of Binary Search in JavaScript
Let's take an example :
Find out the index of "26" out of a sorted array that is given below.
Step-by-Step Process is Given Below to Apply Binary Search on the Above Example:
-
To perform a Binary Search, we'll need to keep track of three variables: startIndex, middleIndex, and endIndex. Let startIndex = 0. endIndex can always be calculated with the help of an array. endIndex = array.length — 1 where length : endIndex = array.length — 1.
-
Using the startIndex and endIndex and dividing by 2, we want to get an initial middleIndex. Due to the even or odd number of elements in the array, it can be a little difficult. We can round down or up with Math.floor() or Math.ceil(), but we'll round down with Math.floor() in this case : let middleIndex Within our While Loop, this will be the only index variable we store. The process will then be repeated until the while loop is terminated. While is used in our case.
-
Let's take a look at the array's 9 total elements. We divide by two and use Math.floor() to round down, which selects a middleIndex at Index 4, where the number "18" is found. We now compare this number "18" to our target number "26" to see which one is greater or less than the other.
-
We know that our target value will be somewhere to the right of the middleIndex if the middeIndex value is less than "26". The current middleIndex value can then be assigned to our startIndex variable, effectively chopping off the left half of the array.
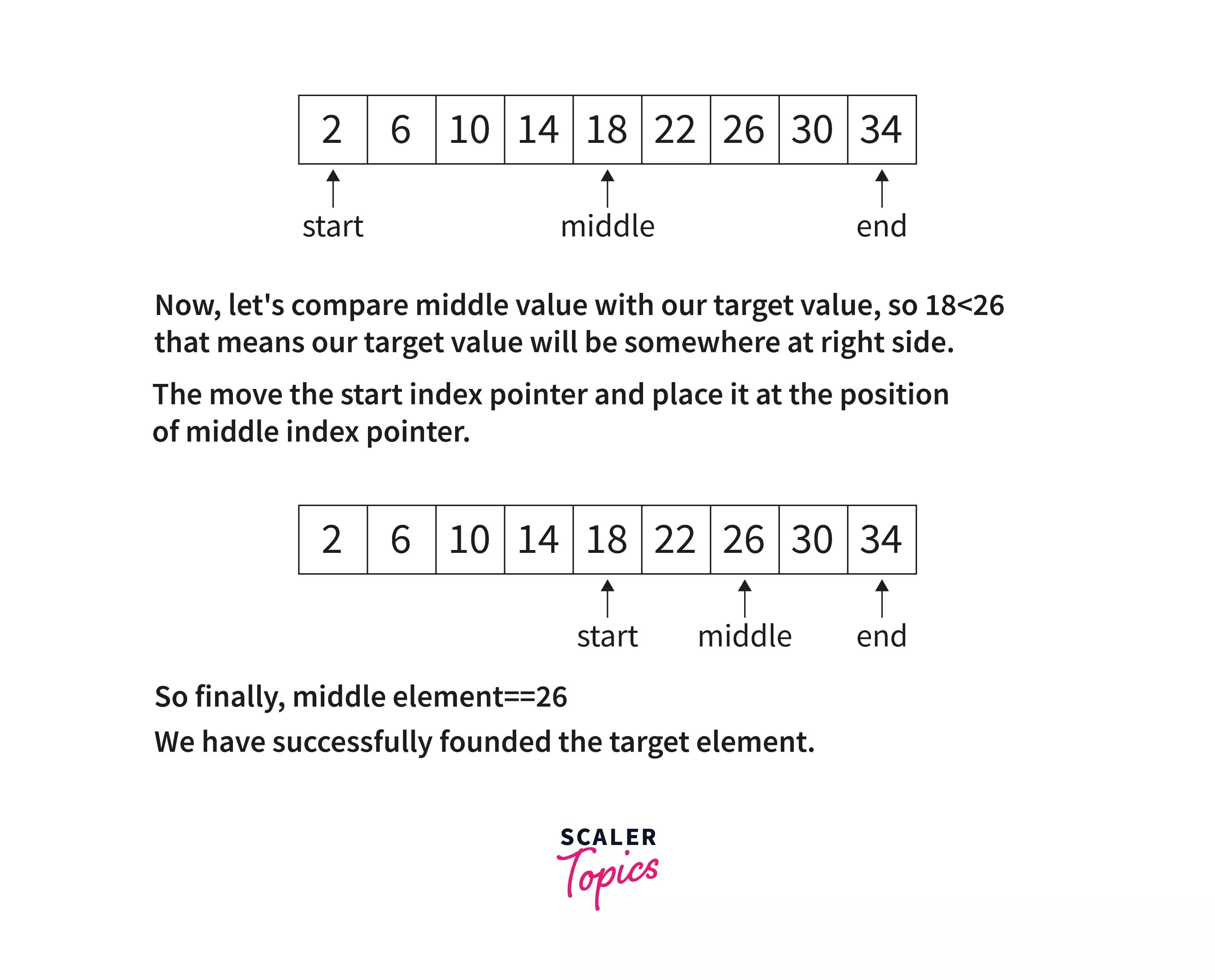
-
We know our target value will be somewhere to the left of the middleIndex if the middeIndex value is greater than the target value of "26". The endIndex variable can then be set to the current middleIndex value, effectively chopping off the right half of the array.
-
We've found our target number that is "26" if the middleIndex value is equal to the target value that is "26". Depending on the size of your array and your target number, the loop may only loop once or dozens of times.
-
Finally, you have completed your Binary Search!
Now let's focus on the two possible approaches or methods to implement the binary search algorithm.
1. Recursive Approach
Steps to apply the recursive approach for binary search in javascript are given as follows.
- BASE CONDITION:
Return false if the start index is greater than the end index. - Calculate the mid index.
- Compare the mid element with the number i(i here is the target value). Return true if the two values are equal.
- If the value is greater, call the same function with a mid-1 as an end index and repeat step 1.
- If the result is smaller, call the same function again with the start index set to mid+1 and repeat step 1.
The following is the JavaScript code for Binary Search (Recursive Approach) :
Output :
Here, if we use binary search using this approach, then the Time complexity will be , and the Auxiliary space will be .
2. Iterative Approach
Instead of recursion, we use a while loop in this iterative approach, and the loop runs until it reaches the base condition, i.e. start becomes greater than the end.
The following is a JavaScript code of Binary Search (Iterative Approach) :
Output:
Here, in this approach also, the Time complexity will be , and the Auxiliary space will be .
Time and Space Complexity of Binary search
Now let's move on to the time and space complexity of the binary search, so the binary search has a time complexity of , here, N is nothing but the number of elements or values that are present there in an array or list. But when it comes to the comparison with the linear search, which has a time complexity of , that's why binary search is far better than linear search.
Binary search performs all the operations over that same original array, it doesn't create the new array, so we can say that binary search work in space.
In both of the cases, the recursive and iterative one, the Time complexity will be , and the Auxiliary space will be .
Time Complexity
Best case time complexity is when the target element was found at the middle index of the array. Due to this, there is only a 1 comparison which is done in only 1 step i.e., the best case time complexity will be .
Worst case time complexity is when the target element was found at the first or last index of the array. Due to this, there will be logN comparisons i.e, worst-case time complexity will be .
Space Complexity
In the case of the iterative(best case) approach, there is only a need for three-pointers(start, end, middle) because all the operations are performed over the original array, and no other extra data storage is required which tends the space complexity to be .
But in the case of the recursive(worst case) approach, there will be recursive calls, suppose if there are x number of comparisons required then x recursive calls will get stacked onto the memory which ends up by taking the memory space.
The Efficiency of Binary Search
We must keep in mind that Binary Search can only be used on sorted arrays. If you use an efficient sorting algorithm, the sorting step has a complexity of . This means that, in most cases, if the array is small or we only need to search it once, a brute-force algorithm (such as Linear Search) may be preferable as it is easy to implement(when the array has few elements) and will not take that much time because of the small size of the array.
Because of this, Binary Search succeeds when we need to perform multiple searches on large arrays. For an array of 11 elements, we only needed 4 comparisons (comparisons being the most time-consuming task of all search algorithms). Suppose we have an array having 10,000,000 elements in it, then if we apply binary search over it, then, only 24 comparisons will be made, which is nothing but the 0.0002% of the total size of the array.
Conclusion
- In this article, we got to know about the Binary search.
- Binary search is a very simple, intuitive and efficient algorithm which can be used to search an element from an array.
- The array must be sorted before applying this algorithm; otherwise, this algorithm will not work.
- Binary search is much more efficient in comparison with linear search.
