Binary Search Tree Python

What is Binary Search Tree in Python?

A Binary Search Tree Python is a special type of tree, i.e., a nonlinear data structure with special properties like 

• Each tree node can have a maximum of 2 children nodes, i.e., left node and right node.
• In each tree node, the value of the left child is less than or equal to its parent node, and the value of the right child will always be greater than or equal to its parent node value.
• Left_Subtree(node) <= node <= Right_Subtree(node)

This leads to the formation of 2 subtrees for each node, where the value of each node is a left subtree containing keys that are less than or equal to the value of the parent node, and each value contained in the right subtree is greater than or equal to the key value of its node.

In Python, in order to implement a Binary Search Tree, we can use object-oriented programming, i.e., we can create a class to represent nodes that will have 3 parameters, i.e., the key, the address of the left node, and the address of the right node.

Binary trees come in a variety of forms, including:

• Complete binary tree: The root key has a sub-tree with two or no nodes, and all levels of the tree are filled.
• Balanced binary tree: A balanced binary tree, also referred to as a height-balanced binary tree, is defined as a binary tree in which the height of the left and right subtree of any node differ by not more than 1.
• Full binary tree: A full binary tree is defined as a binary tree in which all nodes have either zero or two child nodes. Conversely, there is no node in a full binary tree, which has one child node.

Searching in a binary search tree has the worst-case complexity of O(n).

How to Insert a Node in the Binary Search Tree?

In a Binary Search Tree Python, while inserting a node, we need to take care of its property, i.e., left <= root <= right. In this, we try to insert a new key value in an existing Binary Search Tree while retaining its properties and all the existing keys and values.

Algorithm:

• Start from the root node.
• When inserting an element, compare it to the root; if it is smaller than the root, call the left subtree recursively; otherwise, call the right subtree recursively.
• Simply insert the node at the left (if less than current) or the right (if not) after reaching the end.

Code:

Output:

A new key is always inserted at the leaf. We start searching for a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.

How to Search for a Key in a Given Binary Tree?

Description

As the name suggests, searching is the main operation of a Binary Search Tree in Python. Its main task is to find a key in a Binary Search Tree. In order to find the key in an effective manner, we use the Binary Search algorithm, i.e., traversing whether the key is smaller or larger using the Binary Search Tree Property.

If we had had a sorted array, we could have used a binary search to find a value. In binary search, we first identify the entire list as our search space; the number can only exist within the search space. Let's imagine we wish to search for a number in the array. Now, we compare the number to be searched or the element to be searched with the middle element (median) of the search space, and if the record being searched is less than the middle element, we search in the left half; if not, we search in the right half. If the numbers are equal, the element has been found. In a binary search, we start with 'n' elements in the search area and if the mid element does not match the element for which we are searching, we decrease the search space to 'n/2'. We keep lowering the search area till we either discover the element that we are searching for or we get down to just one element in the search area and are done with this entire reduction.

Let's see the algorithm and code for searching in a Binary Search Tree.

Implementation in Python

Output:

Let’s say we want to search for the number, we start at the root, and then we compare the value to be searched with the value of the root, if it’s equal we are done with the search if it’s smaller we know that we need to go to the left subtree because in a Binary Search Tree Python all the elements in the left subtree are smaller and all the elements in the right subtree are larger.

Illustration of Searching for a Key

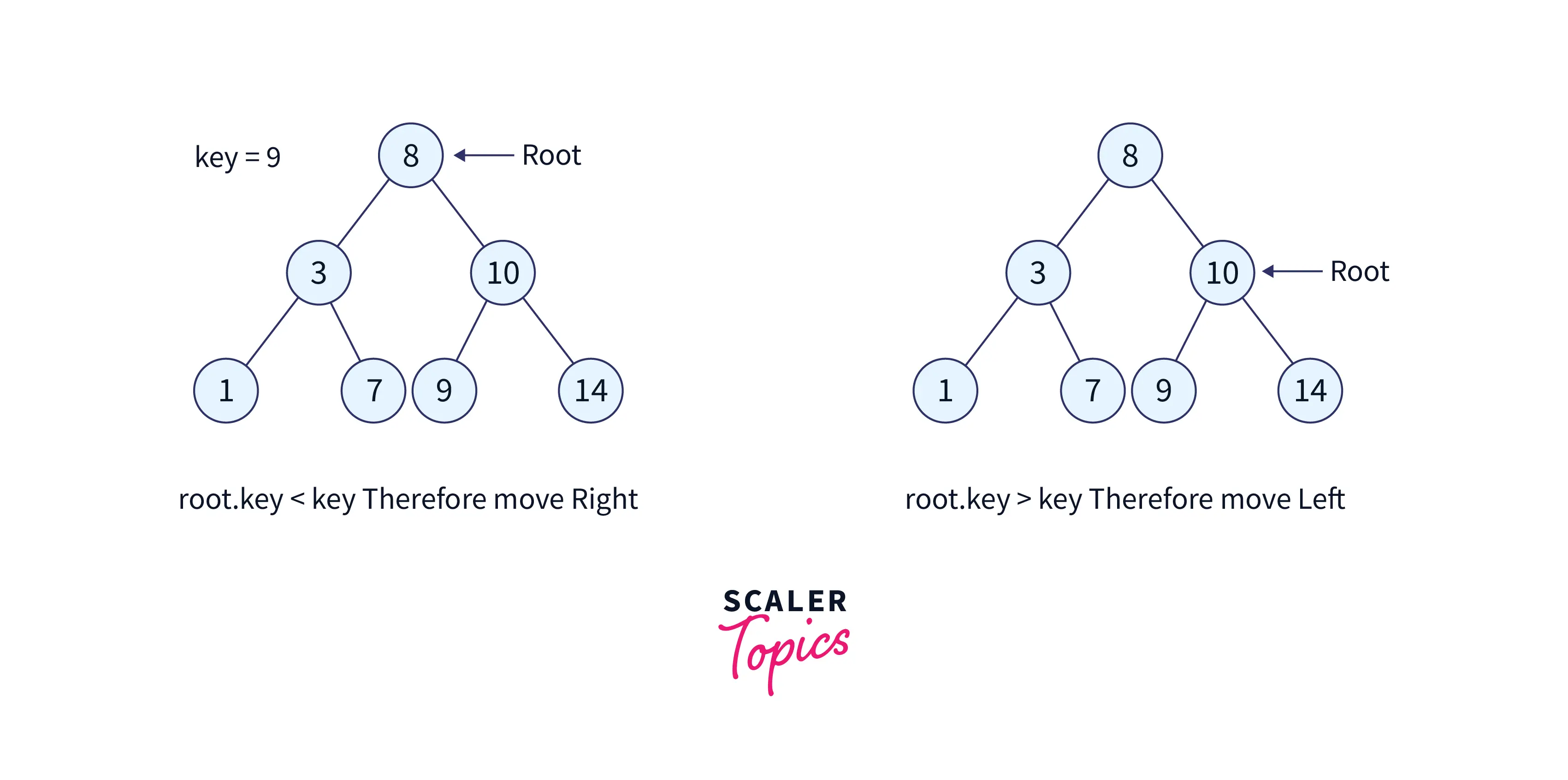
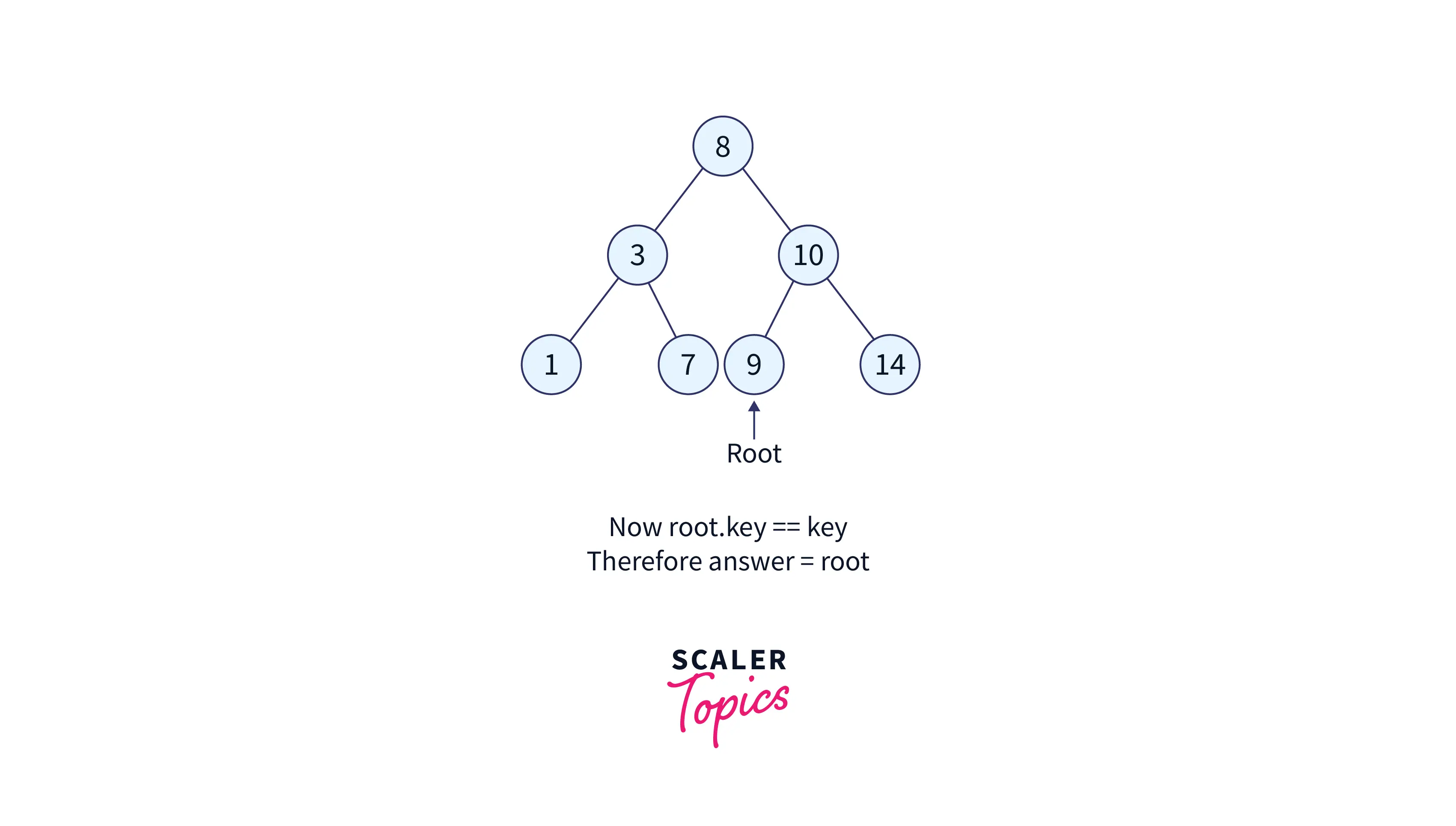
Search and insert operations have a worst-case time complexity of O(h), where h is the height of the Binary Search Tree. The worst-case scenario is that we might have to go from the root to the deepest leaf node. The worst-case time complexity of a search and insert operation may be O(n), while the height of a skewed tree may be n.

How to Delete a Node in the Binary Search Tree?

Deleting is one of the most important tasks of a Binary Search Tree Python, i.e., removing a node from the existing node without affecting the structure of the tree, other keys, or the property of a Binary Search Tree. It has three cases for deleting a node in a Binary Search Tree.

Case 1: The leaf node in the first scenario is the node that has to be eliminated. Simply remove the node from the tree in this situation.

Case 2: The node that has to be eliminated in the second scenario has just one child node. Do the following actions in this situation:

• Put its descendant node in its place.
• The child node should be moved from its starting location.

Case 3: In the third scenario, the removed node has two offspring. Do the following actions in this situation:

• Obtain that node's in-order successor.
• Put the in-order successor in place of the node.
• The in-order successor should be moved from its initial location.

Code:

Output:

In the above output, first, we have 7 nodes in the tree, then we deleted node 20 from the tree, so our modified tree would have 6 nodes i.e. 30 40 50 60 70 80.

Some Interesting Facts about Binary Search Tree Python

• BST's inorder traversal always results in the sorted output.
• Only preorder, postorder, or level order traversal is required to build a BST. Keep in mind that by sorting the only supplied traversal, we can always obtain an in-order traversal.

Related articles

• Binary Search Tree (BSTs)
• Binary Tree in Data Structure
• Tree Data Structure