Binary Tree in C – Types and Implementation

In C, a binary tree is a hierarchical data structure with nodes limited to two children each. Nodes contain a value and pointers to the left and right children. The longest root-to-leaf path defines the tree's height. Implementation in C uses structures with pointers or arrays, where children of a parent node at index P are at indices (2P+1) and (2P+2).

What are Trees in C?

The tree is a non-linear data structure in C that contains nodes that are not connected linearly. Rather they are connected hierarchically. The nodes are present at different levels and are connected by edges. Between the set of two connected nodes, the one which is at the upper level is considered a parent, and the lower one is considered a child node.

In Tree in C, a parent node can have many children nodes. The diagram below shows the structure of the tree in C.

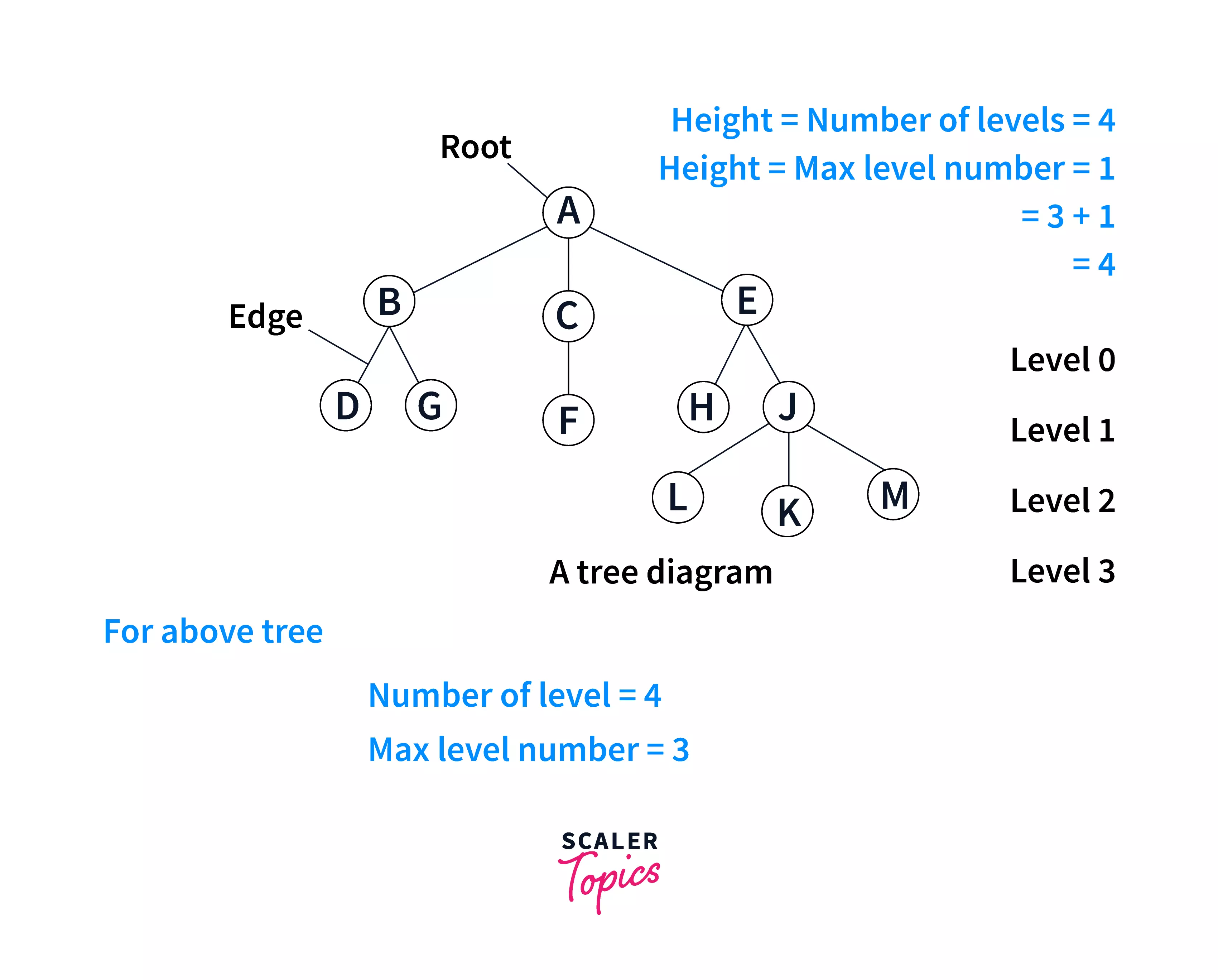
In the above image of the tree, A is the root node. B, C, and E are the children of node A; they have 2, 1, and 2 children, respectively. Here, D, G, F, H, L, K, and M are the leaf nodes.

A binary tree in C is a special case of the tree, which can have only two children nodes (left child and right child).

Tree Terminologies

Various terminologies are related to the tree :

1. Root :
   The first node of the binary tree is known as the root node of the binary tree. There cannot be any tree without a root node, as it is the tree's origin, and the root node has no parent element. We cannot have more than one root node in a tree.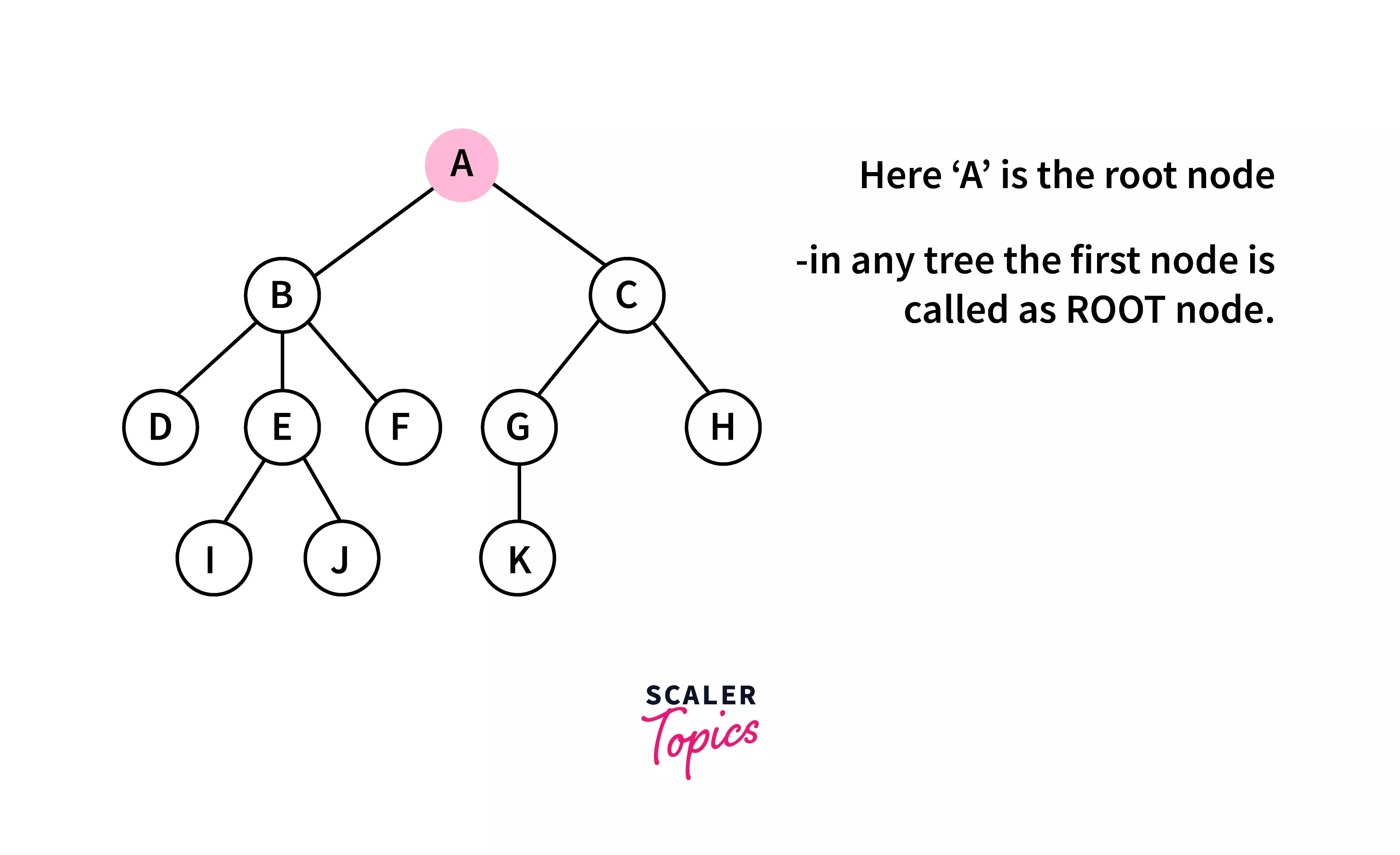

2. Edge :
   The connecting link between the two nodes is known as the edges of the tree. It is also referred to as the branch of a tree. If there are n nodes in a binary tree, there will be a total of n-1 edges.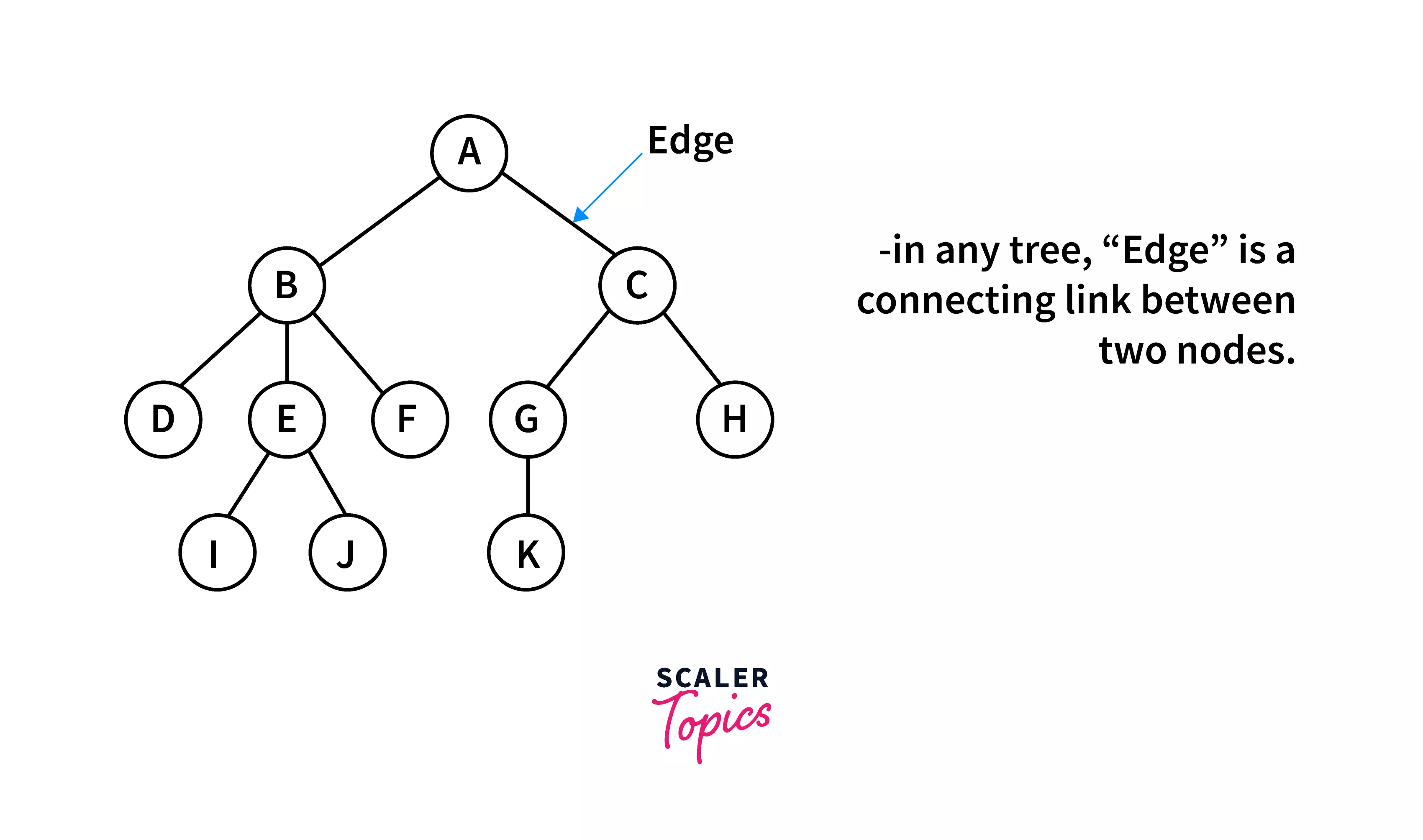

3. Parent :
   A node that has a connecting link to another node in the level below is known as a parent node. In a more formal term, a node that is a predecessor of another node is called a parent node.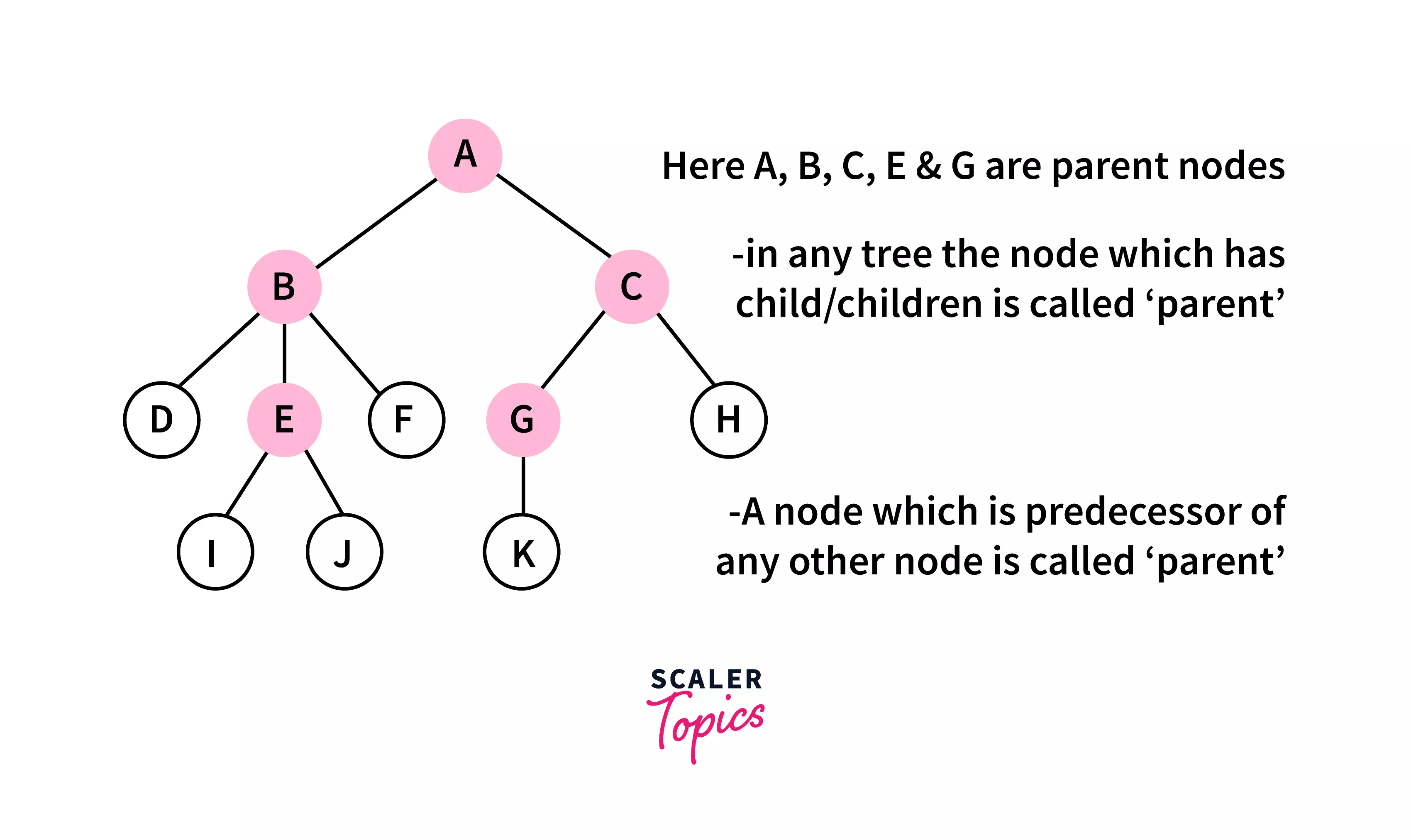

4. Child :
   Any node connected to a node one level above it is known as the child node. In formal terms, every note that is a descendant of any node is known as a child node. Every not present in the tree can be considered as a child node except the root node.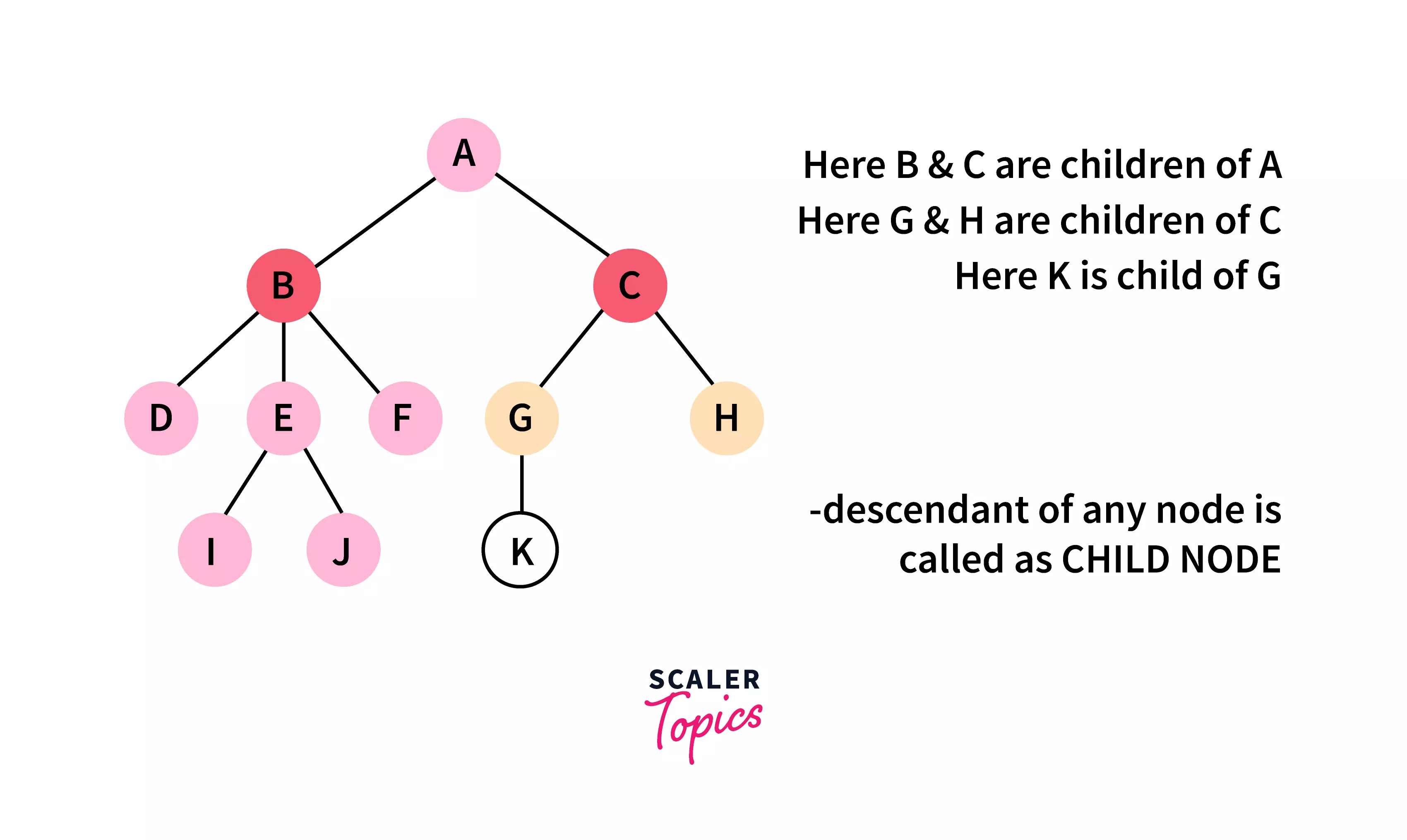

5. Siblings :
   The children node that shares the same parent node are referred to as siblings.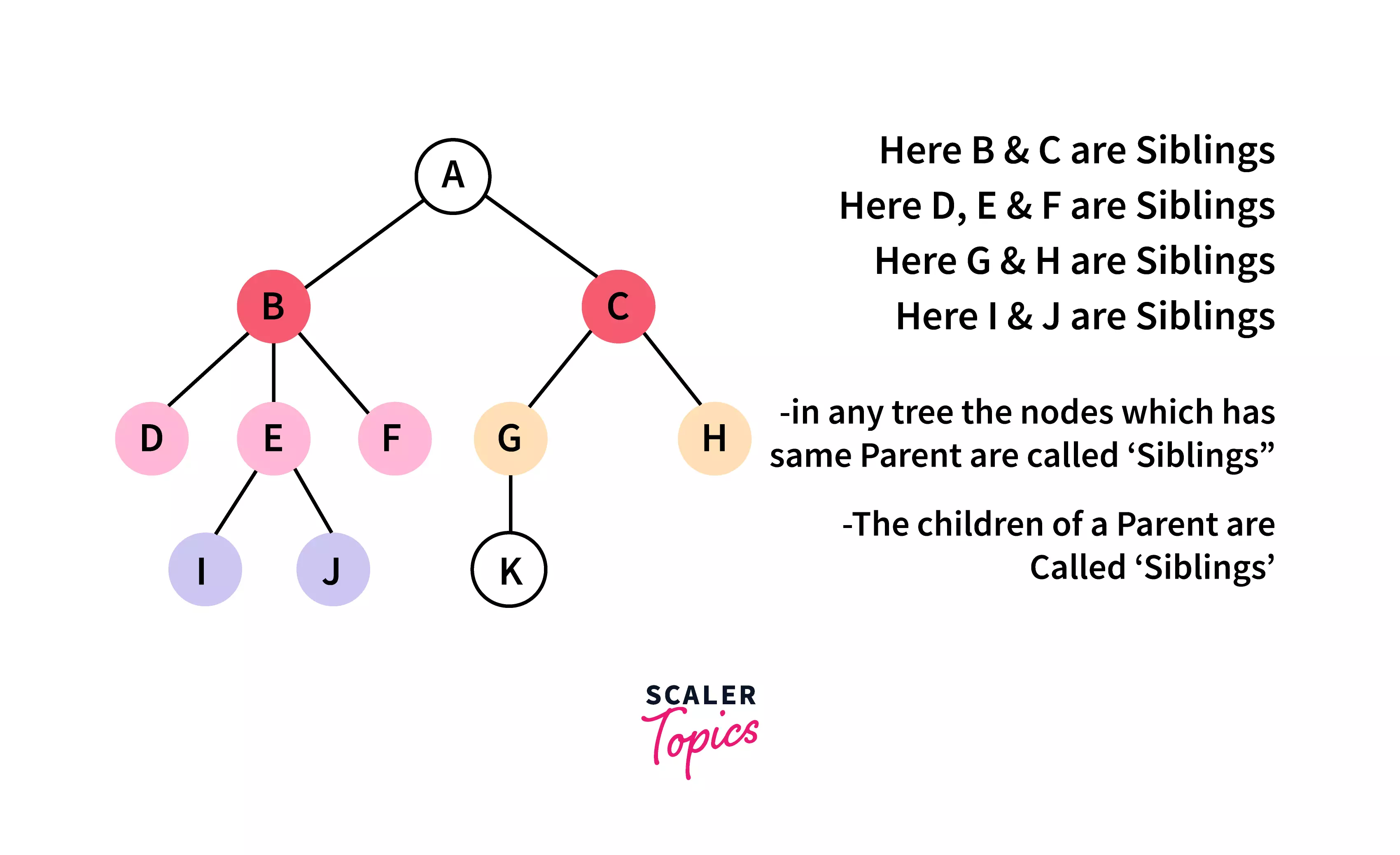

6. Leaf :
   A node with no child is known as a leaf node. It is the terminal node of the tree.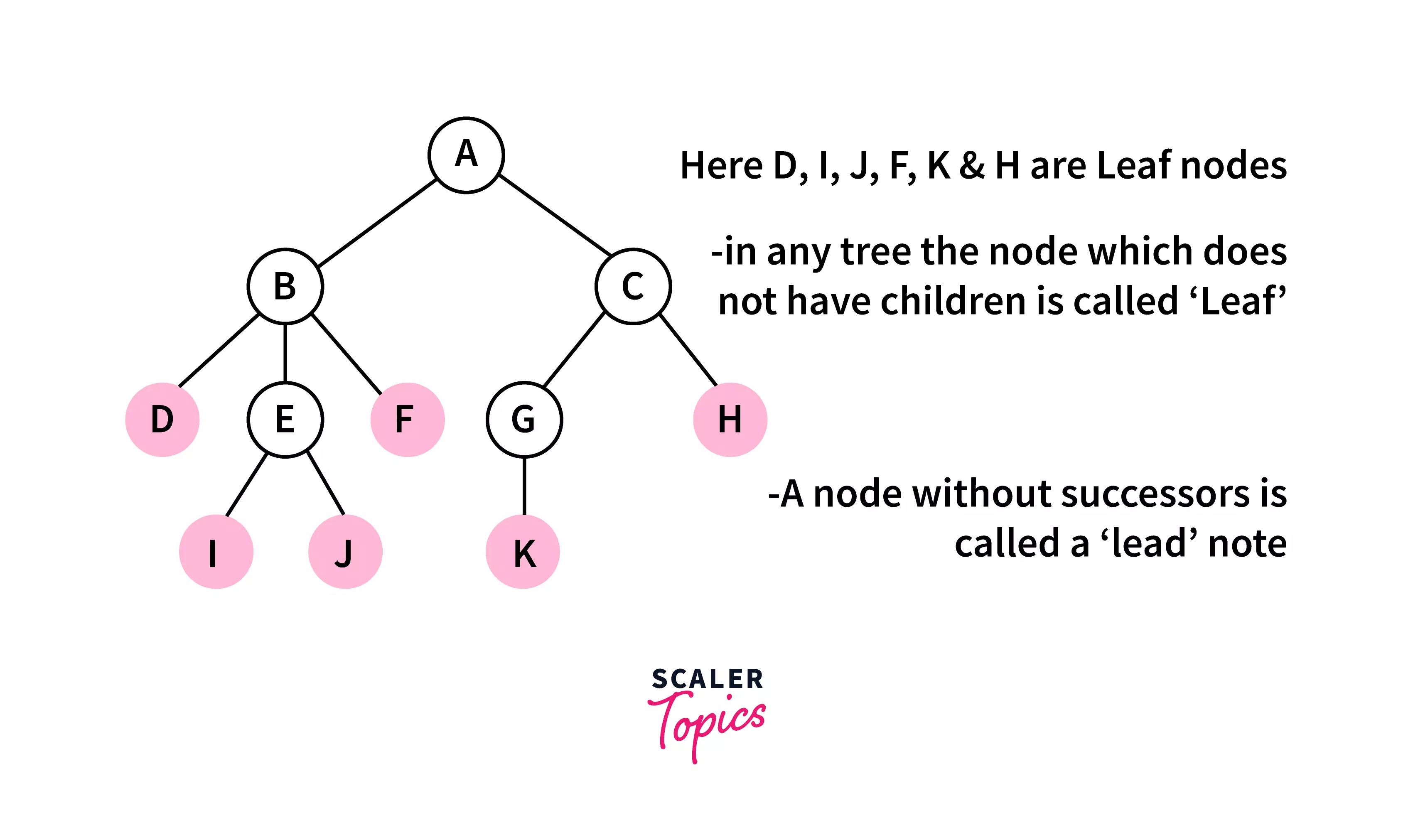

7. Internal Node :
   The nodes with at least one child node are known as internal nodes. Every node (even the root node) is internal except the leaf nodes.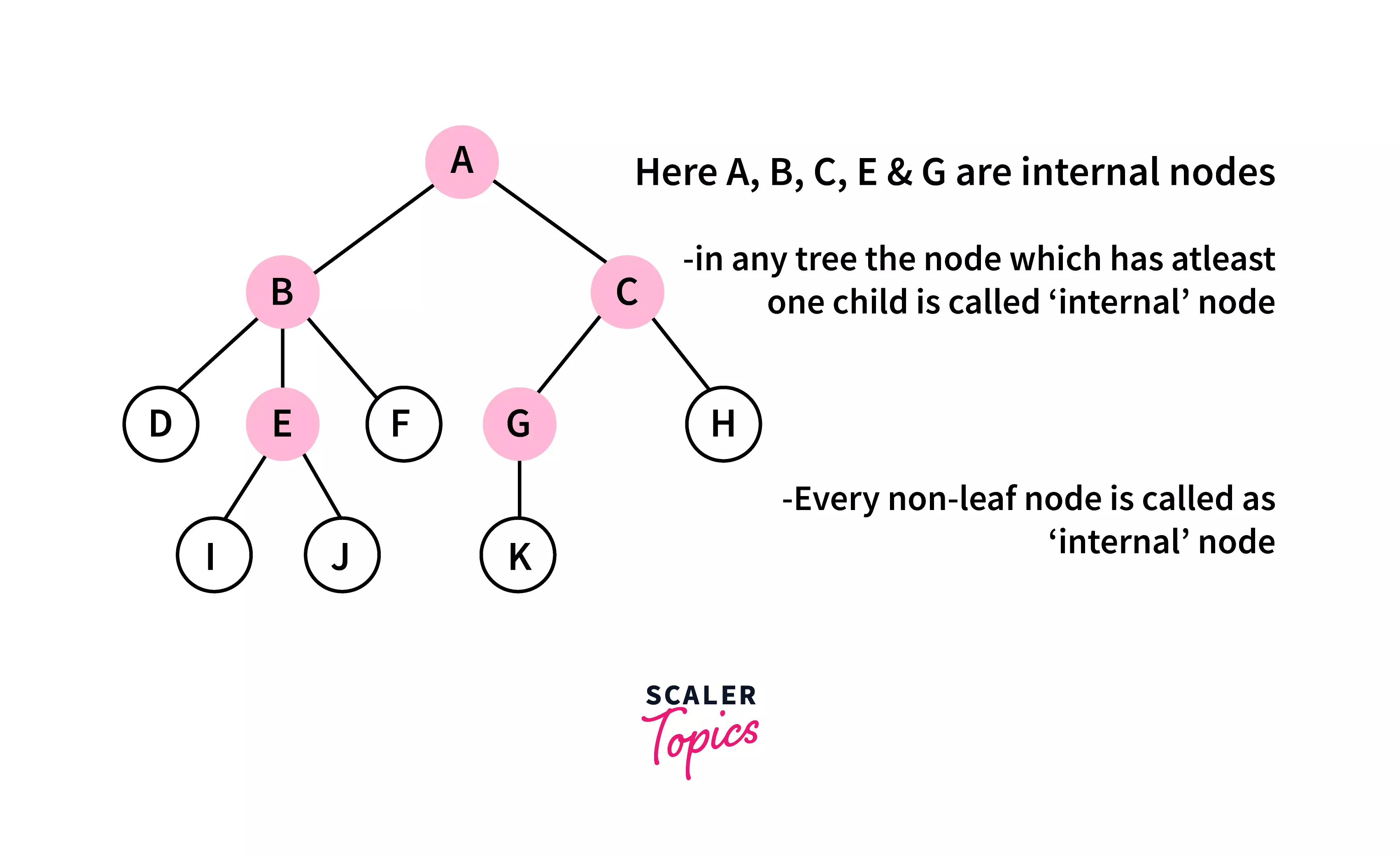

8. External Node :
   A node with no child node is considered an external node.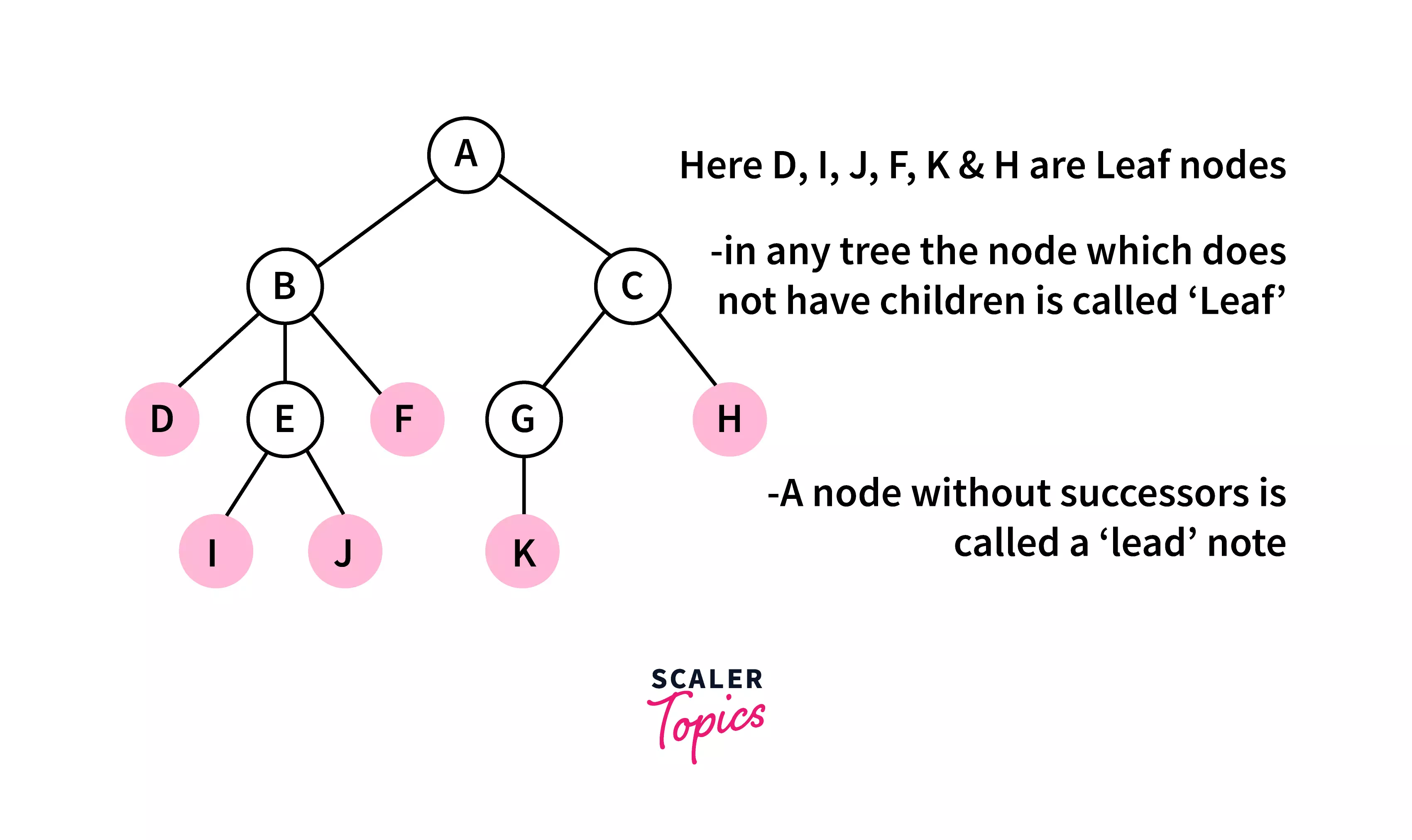

9. Ancestors :
   Ancestors of a node are the nodes in the path from the root to the current node, including the root node, and excluding the current node are ancestors of the current node.

10. Descendants :
    Descendants of a node are the nodes below its level and connected to it directly or via nodes. All the children, their children, and so on are the descendants of the current node.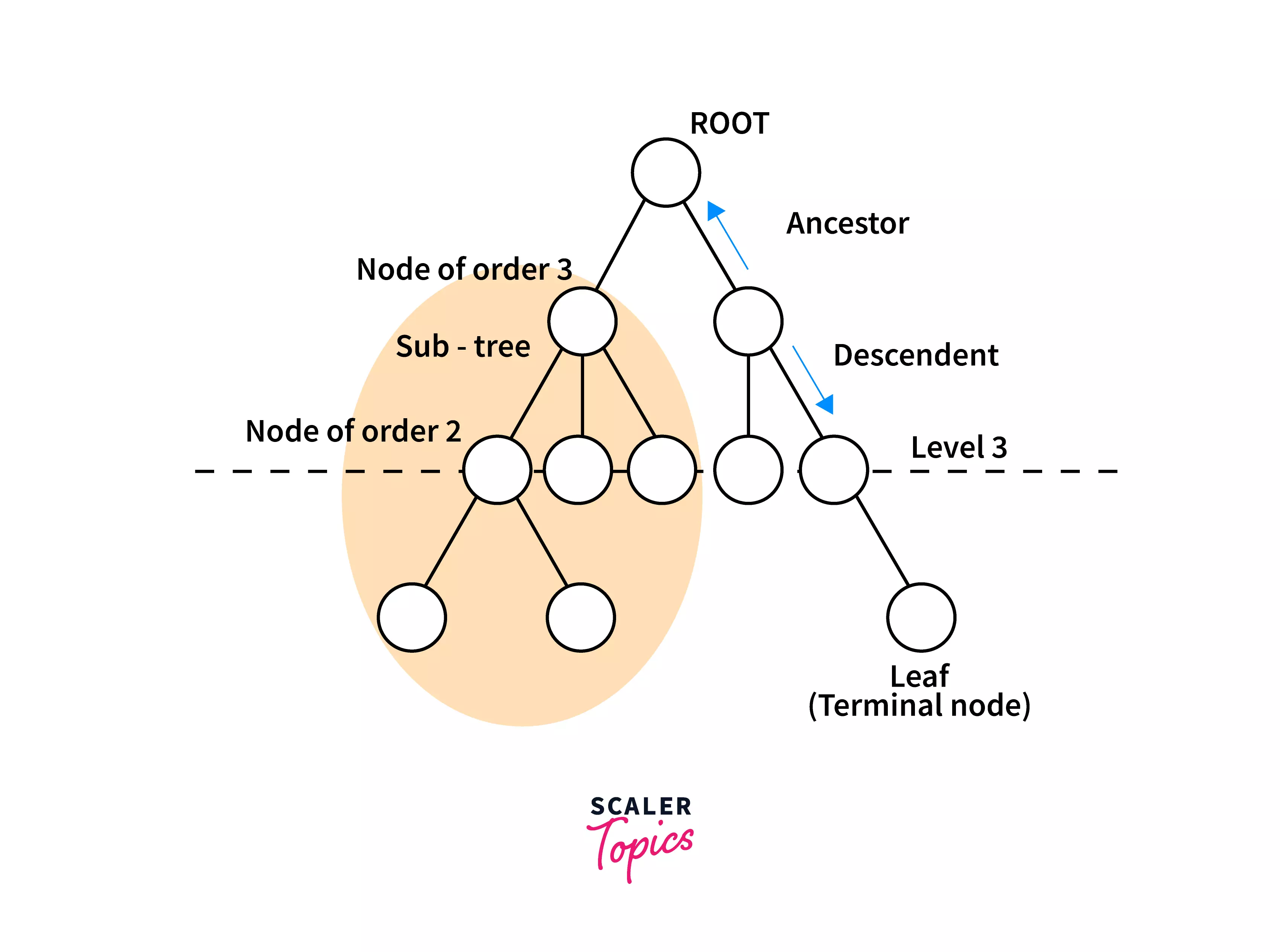

11. Path :
    A path between any two nodes of a tree is the sequence of connected nodes along with the edges between the two nodes. And the path length is the number of nodes present between two nodes.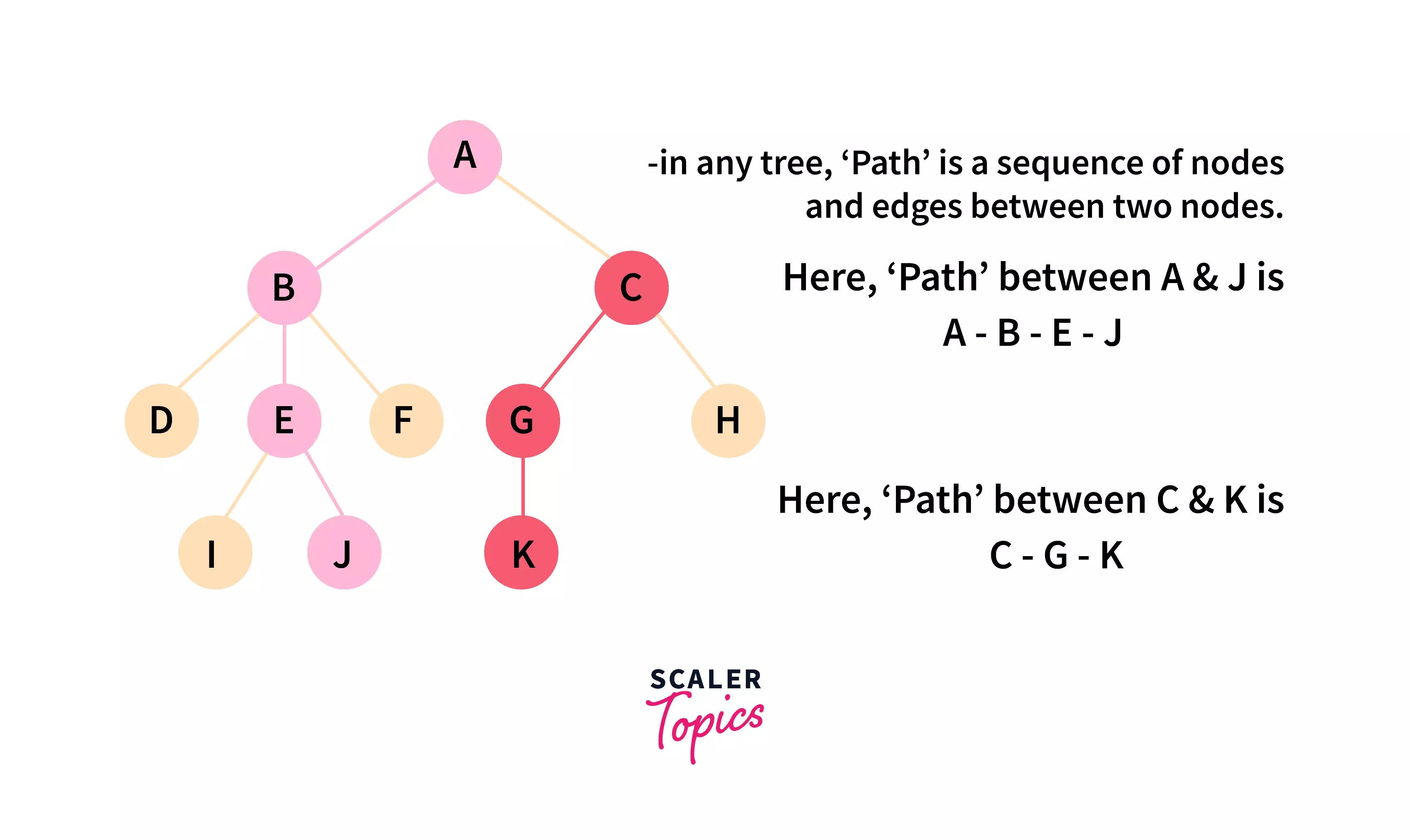

12. Level :
    The level in the tree represents the number of steps from the top/root. The root node of the tree is said to be at level 0, and as we go downwards the level increases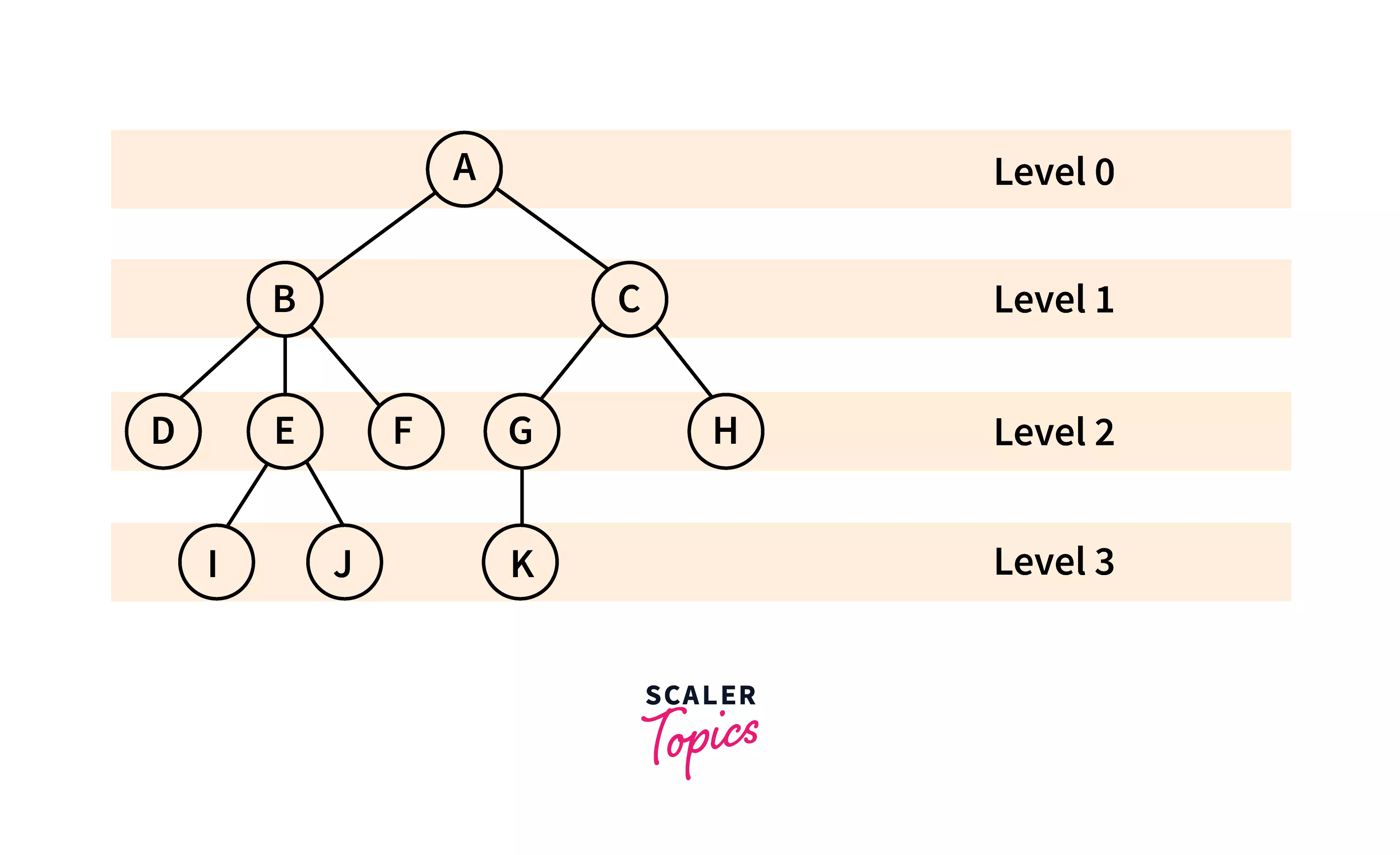

13. Depth :
    The depth of any node in the tree is the length of the path from the root node to that particular node, i.e., The number of nodes between that particular node and the root node.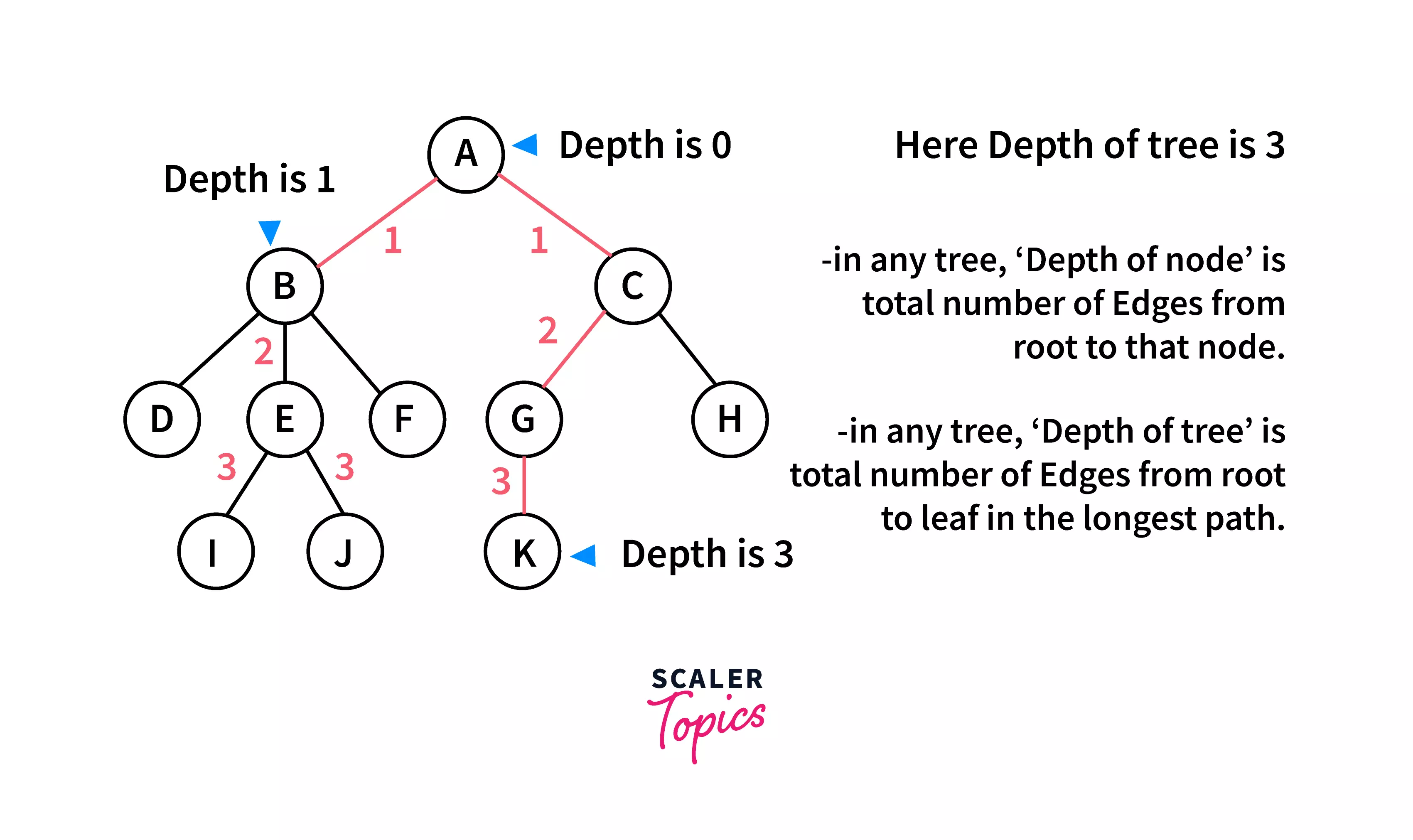

14. Height :
    The height of any node is given by the maximum number of edges from the leaf node to that particular node.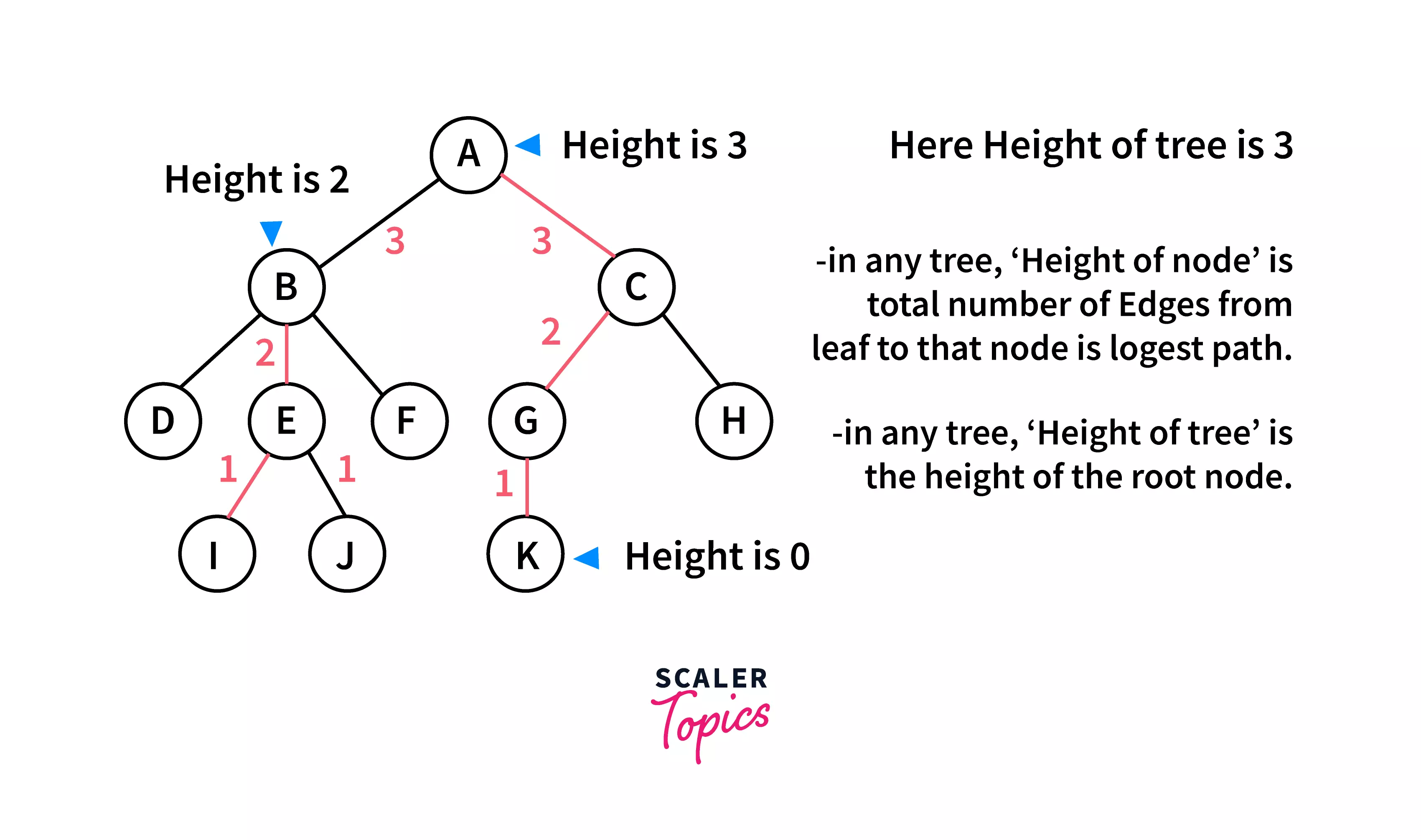

Representation of Binary Tree in C

A binary tree can be represented using a linked list and also using an array. Representation of this tree, using both(array and linked list) is explained below.

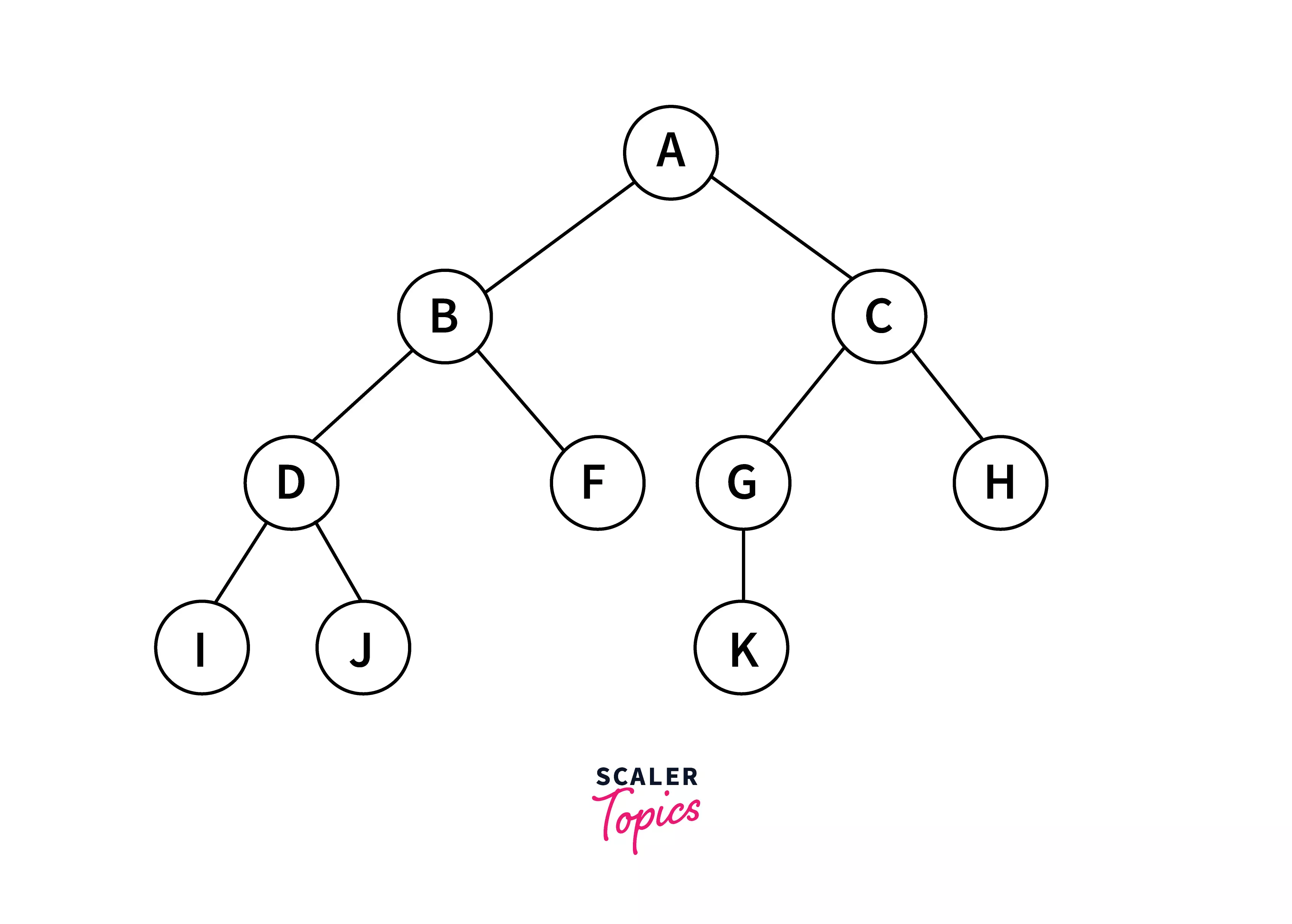
Array Representation :

The binary tree can be represented using an array of size 2n+1 if the depth of the binary tree is n. If the parent element is at the index p, Then the left child will be stored in the index $(2p)+1$, and the right child will be stored in the index $(2p)+2$.

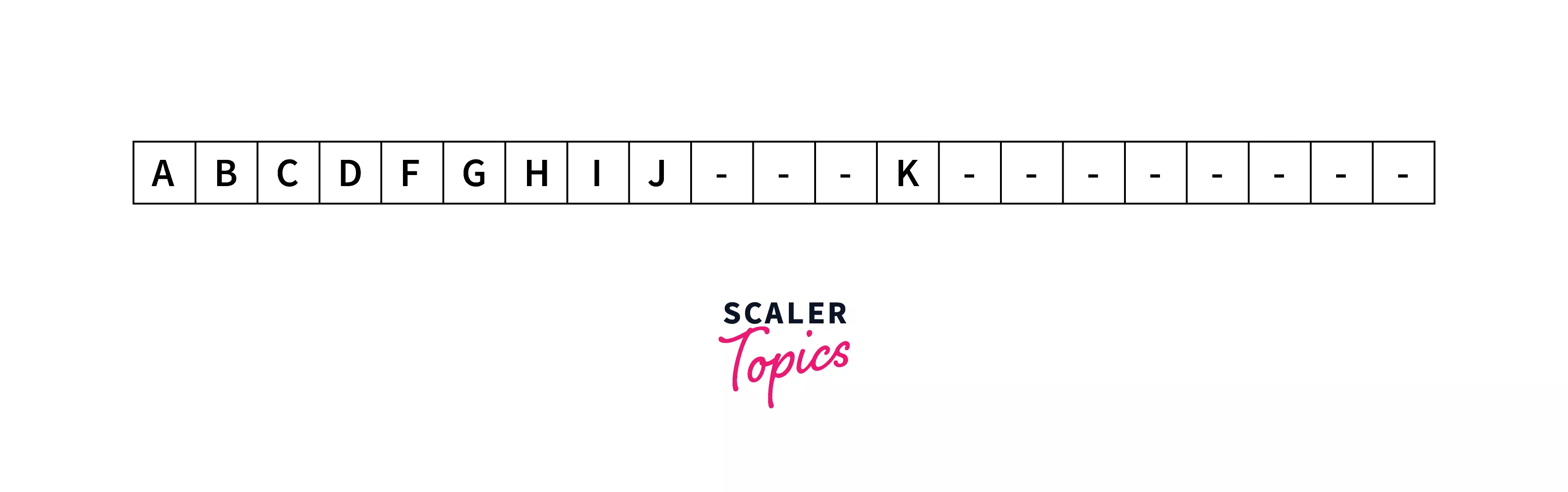
The array representation of the above binary tree is :
As in the above binary tree, A was the root node, so that it will be stored in the 0th index. The left child of A will be stored in the 2(0)+1 equal to the 1st location. So, B is stored in index 1. And similarly, the right child of A will be stored in the 2(0)+2 index. For every node, the left and right child will be stored accordingly.

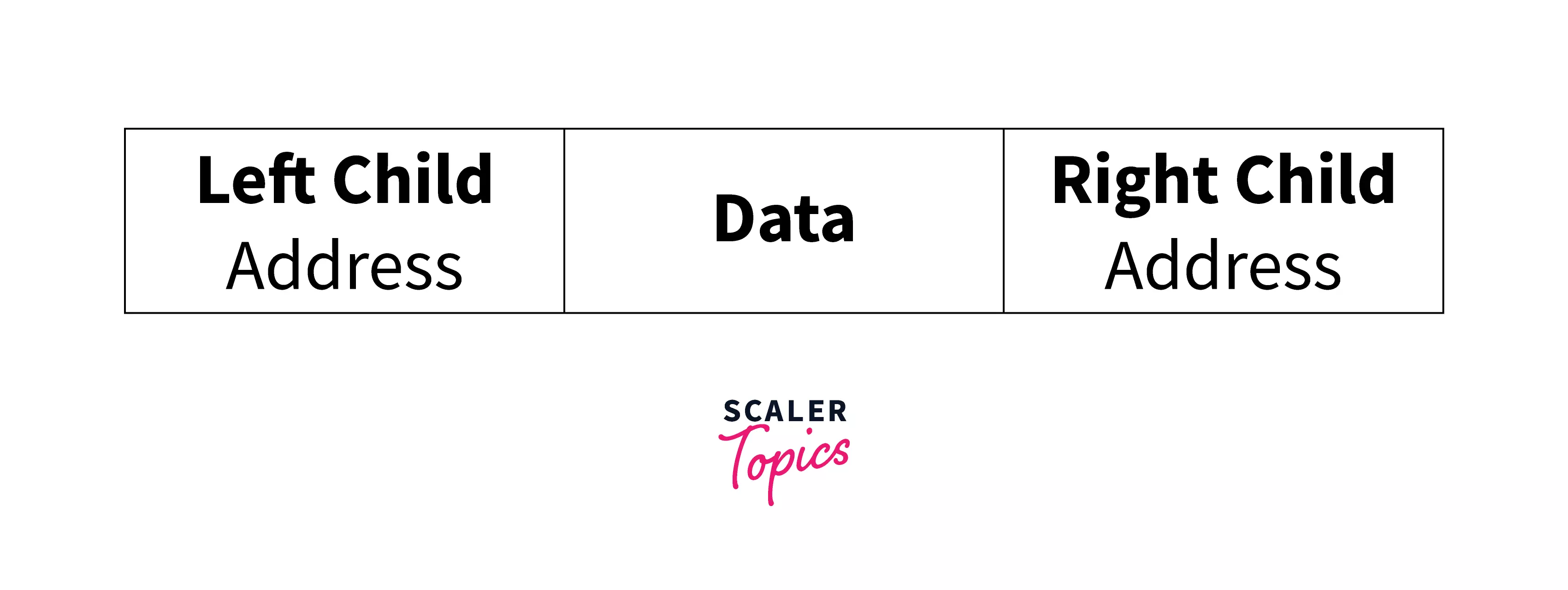
Linked List Representation :

For the linked list representation, we will use the doubly linked list, which has two pointers so that we can point to the left and right children of a binary tree node. NULL is given to the pointer as the address when no child is connected.

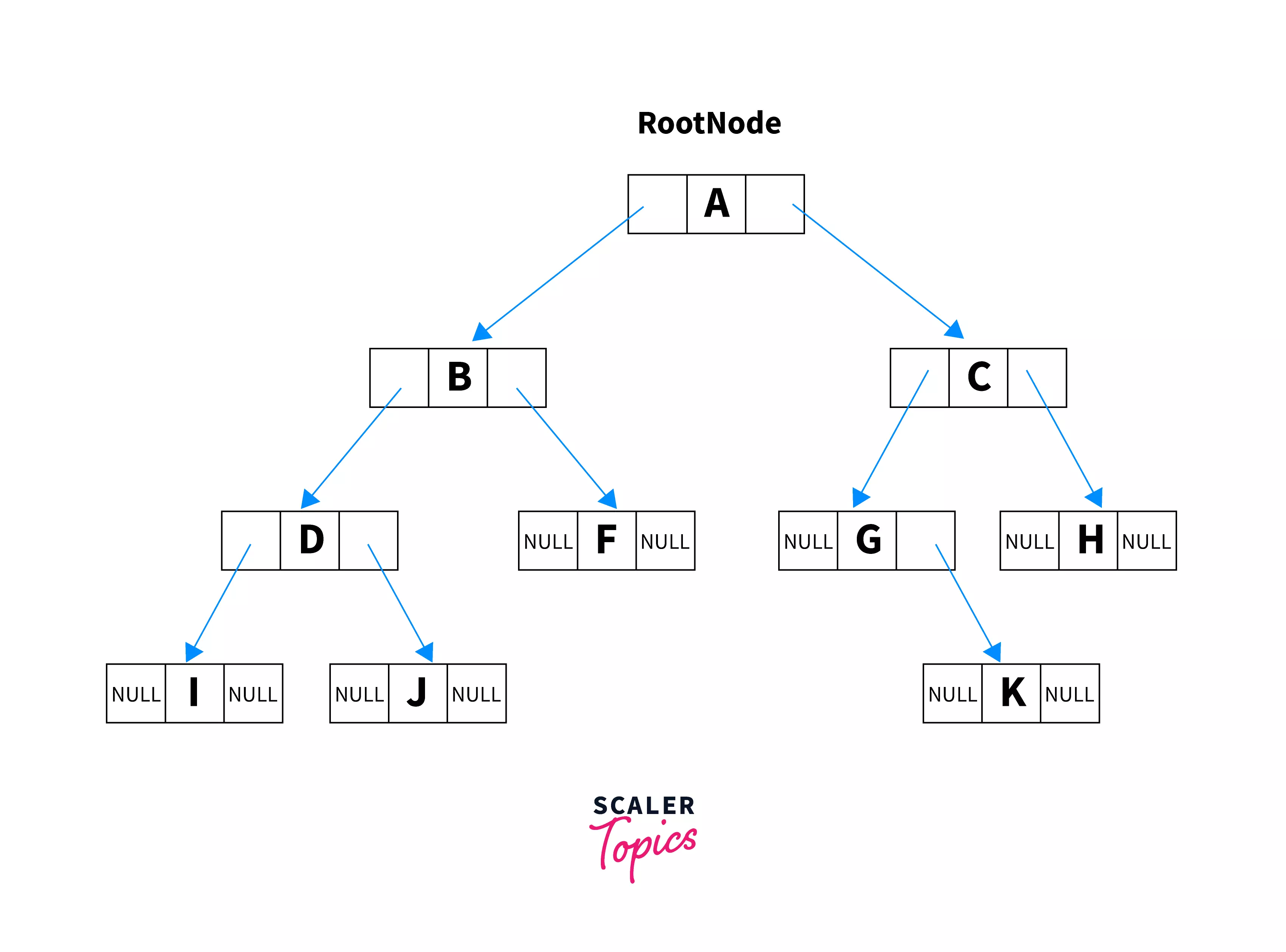
The Linked list representation of the above binary tree is :

Need for Binary Trees

1. Searching becomes easy and faster with the help of a binary search tree, even for huge data sets.
2. Trees do not have a limit on the nodes. So, according to the user's need, a tree of any size can be created and further increased, unlike an array.
3. It can store hierarchical data in the database.
4. A binary tree can also be used for classification and decision-making.

Implementation of Binary Tree in C

The binary tree is implemented using the structure. Each node will contain three elements, the data variable, and the 2 pointer variables. We will use a user-defined datatype (structure) to create the nodes. The node will point to NULL if it doesn't point to any children.

Declaration of a Binary Tree in C

To declare the nodes of the binary tree, we will create a structure containing one data element and two pointers of the name left and right.

Code :

Create a New Node of the Binary Tree in C

To create a new node of the binary tree, we will create a new function that will take the value and return the pointer to the new node created with that value.

Code :

The new node which is being created will have the left and right pointers, pointing at null.

Inserting the Left and/or the Right Child of a Node

This function will take two inputs, first the value that needs to be inserted and second the node's pointer on which the left or the right child will be attached. To insert into the left side of the root node, we will simply call the create function with the value of the node as a parameter. So that a new node will be created, and as that function returns a pointer to the newly created node, we will assign that pointer to the left pointer of the root node that is being taken as input.

Similarly, insertion on the right side will call the create function with the given value, and the returned pointer will be assigned to the write pointer of the root node.

Code :

Traversal of Binary Tree

We can traverse the element tree and can display these elements in three formats/methods :

In every traversal method of the binary tree, we need to visit the left node, the right node, and the data of the present/current node(root). Three methods will have these three actions in a different order.

Pre-Order :
In this type of traversal, first, we will take the value of the current node(present node), then we will go to the left node, and after that, we will go to the right node.

Code :

In-Order :
In this type of traversal, first, we'll go to the left node, then we'll take the value of the current node, and then we will go to the right node.

Code :

Post-Order :
In this type of traversal, first, we'll go to the left node, then to the right node, and at last, we will take the current node's value.

Code :

Example : Implementation of Binary Tree in C

Here in this example, we will use the functions we learned above to create a binary tree, and then we will traverse that binary tree in three different methods.

A structure node is declared, containing a data variable and two pointer variables.

First, we have declared a function create, which takes a value as an input and creates and returns a node that will have the data variable equal to the value, and the left and right pointer variables will point to NULL.

To insert the left child, we will use the insertLeft function, which takes the pointer to the parent node and the value. Then internally, it calls the create function, and the node returned by it is attached to the left pointer of the parent node. Similarly, the insertRight function works.

Code :

After creating the tree, we traversed it using the Inorder, Preorder , and Postorder traversal methods, and we got the following output.

Output :