Convert Binary Tree to Doubly Linked List - Part ii

Problem Statement

Given a Binary Tree convert it into a Doubly Linked List (DLL) where the left and right pointers are modified to the previous and next pointers of the resultant Doubly linked list. The order of nodes in the doubly linked list should be the same as the order of the nodes in the Inorder traversal of the binary tree. Therefore the first node(head) of a doubly linked list will be the leftmost node of the binary tree since we are following Inorder traversal.

In Part 1 of this editorial we discussed three approaches, namely -

• Approach 1: By Processing Subtrees
• Approach 2: Fixing Left and Right Pointers
• Approach 3: Inorder Traversal (By Keeping Track Of DLL Head and Tail Pointers)

In this part we will discuss about recursive and iterative approaches.

Example

For a better understanding of the problem statement, let's look at the below example:

Input:

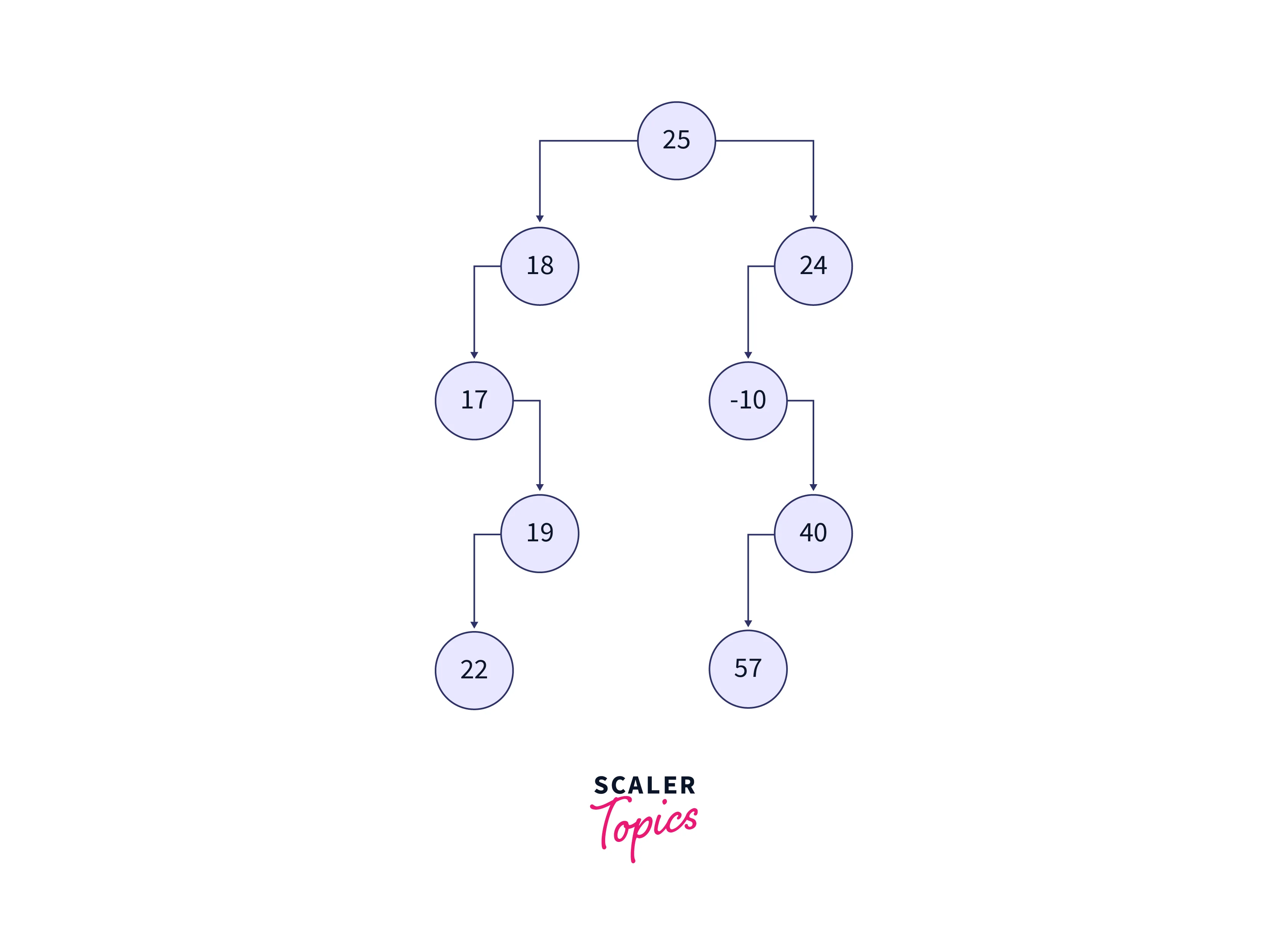
Consider the input binary tree shown in the below image:

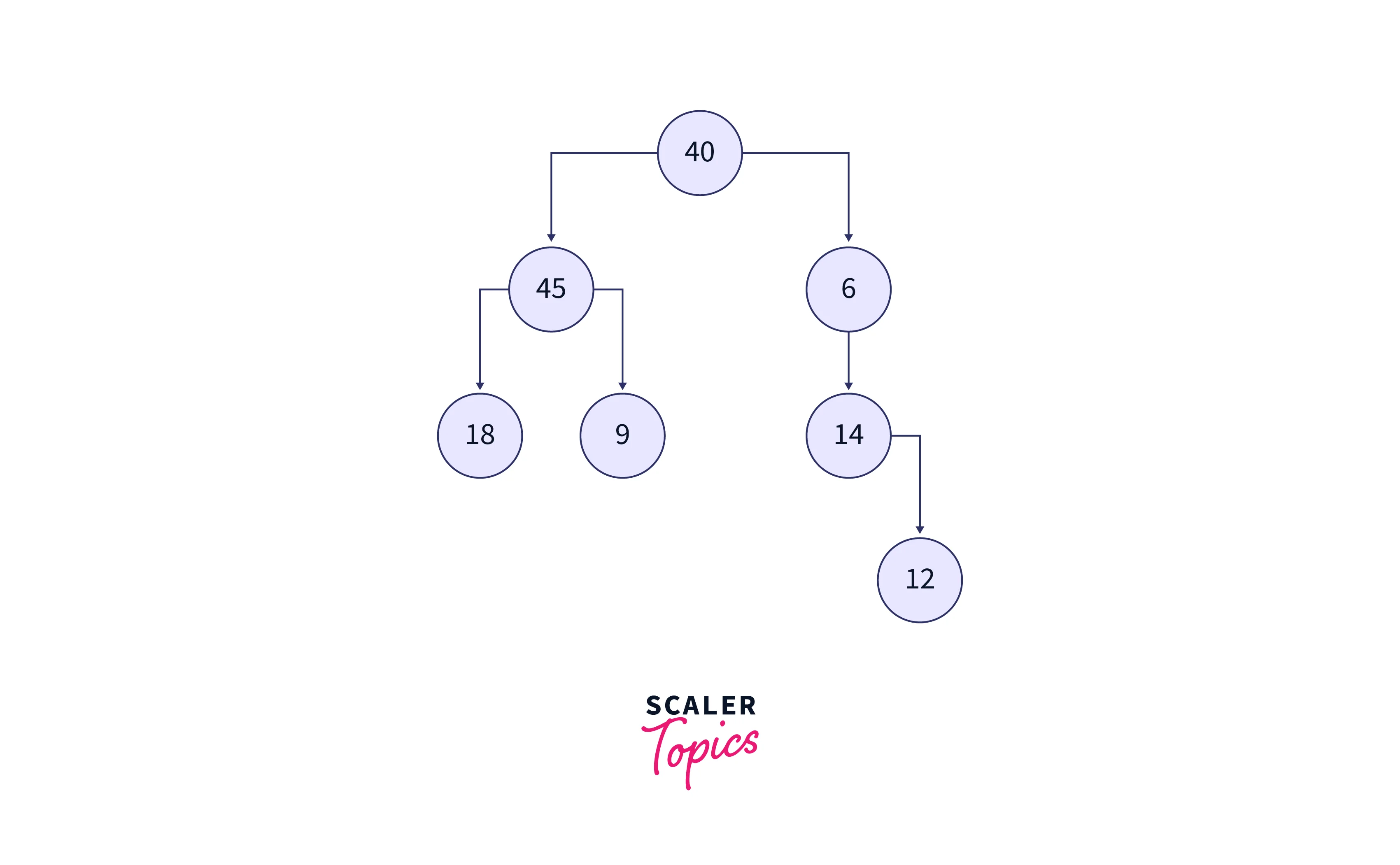
Output:

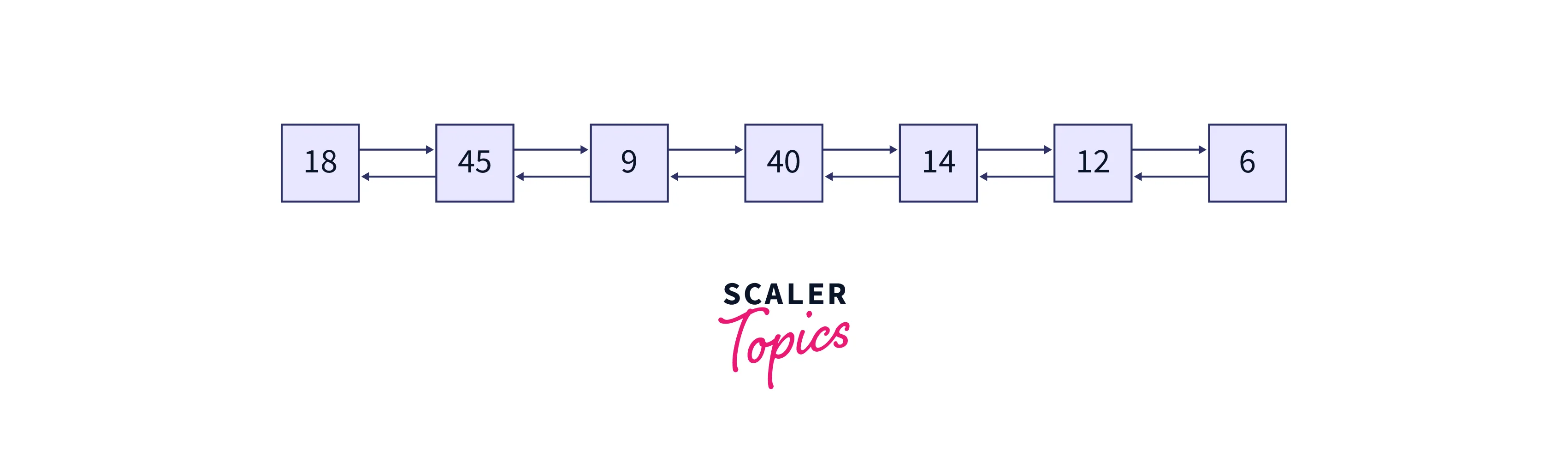
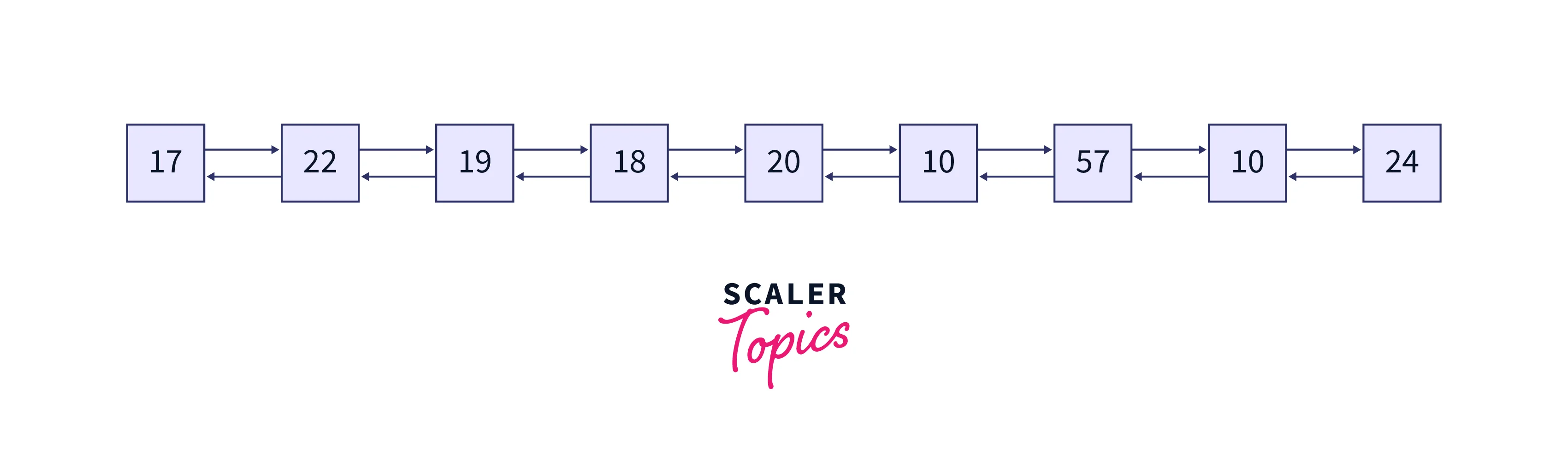
The doubly linked list formed is shown in the below image:

Example Explanation

We can observe that the order of the doubly linked list is the same as the Inorder traversal on the given binary tree. Therefore the nodes of the modified doubly linked list are printed as the output.

Input Format

During competitive programming, the input of the binary tree is given by indicating the value of the data field in each node by providing the root of the binary tree.

Output Format

The output includes printing the node's values of the newly formed Doubly linked list. Print all the nodes in the doubly linked list.

Constraints

• $1 <= N$ (Number of nodes in the binary tree) $<= 10^5$
• Value in the data field can be any real number.

Approach 4: Using Recursion

This approach uses recursion to convert the given input binary tree into a doubly linked list. This solution is considered to be the simplest of the above approaches. This approach also uses Inorder traversal for manipulating the pointers of the binary tree to convert to a doubly linked list. In this approach, while performing an Inorder traversal on the given binary tree we need to keep track of previously visited nodes. In this approach we are just manipulating the right and left pointers to next and prev pointers of DLL unlike the above approach using tail pointer. We follow the Inorder traversal manner so that we can change the left and right pointers as the prev and next pointers to convert them into the doubly linked list.

Algorithm

Below algorithm clearly explains the above approach:

• Start traversing the given binary tree in an Inorder fashion, for every visited node follow the below steps:
  • Keep track of the previously visited node in a variable, assume previous.
  • And for every visited node, make its next pointing to the previous and previous of this node as the prev.
• In this Inorder fashion given input binary tree is converted into a doubly linked list.

Implementation

Below is the implementation of the approach which is discussed above for converting the given binary tree to the doubly linked list

C++ implementation for converting the given binary tree to the doubly linked list by processing subtrees:

Python implementation for converting the given binary tree to the doubly linked list by processing subtrees:

Java implementation for converting the given binary tree to the doubly linked list by processing subtrees:

Output:

Explanation: We can observe that the order of the doubly linked list is the same as the Inorder traversal on the given binary tree. The input binary tree is shown in the below image.

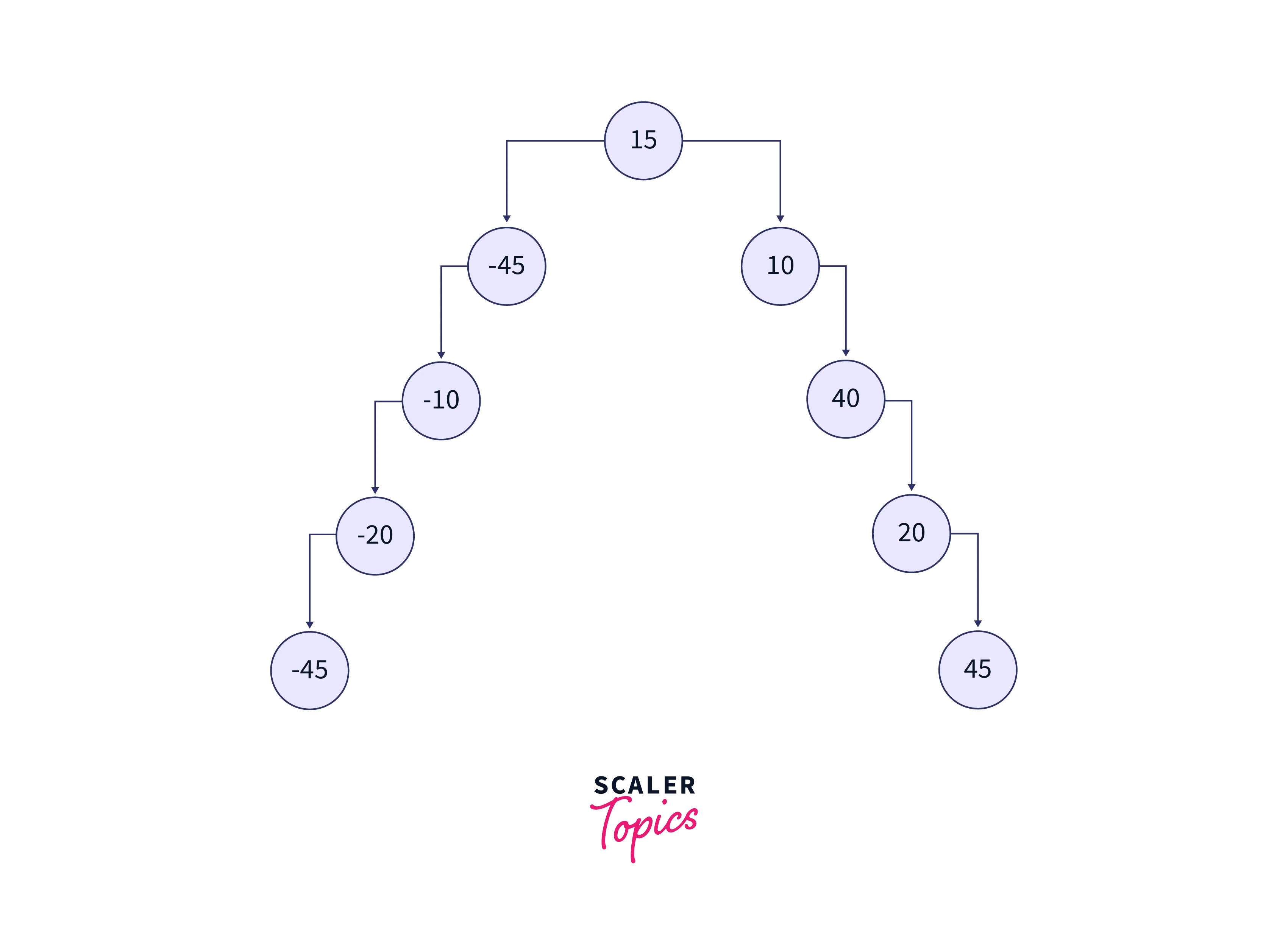
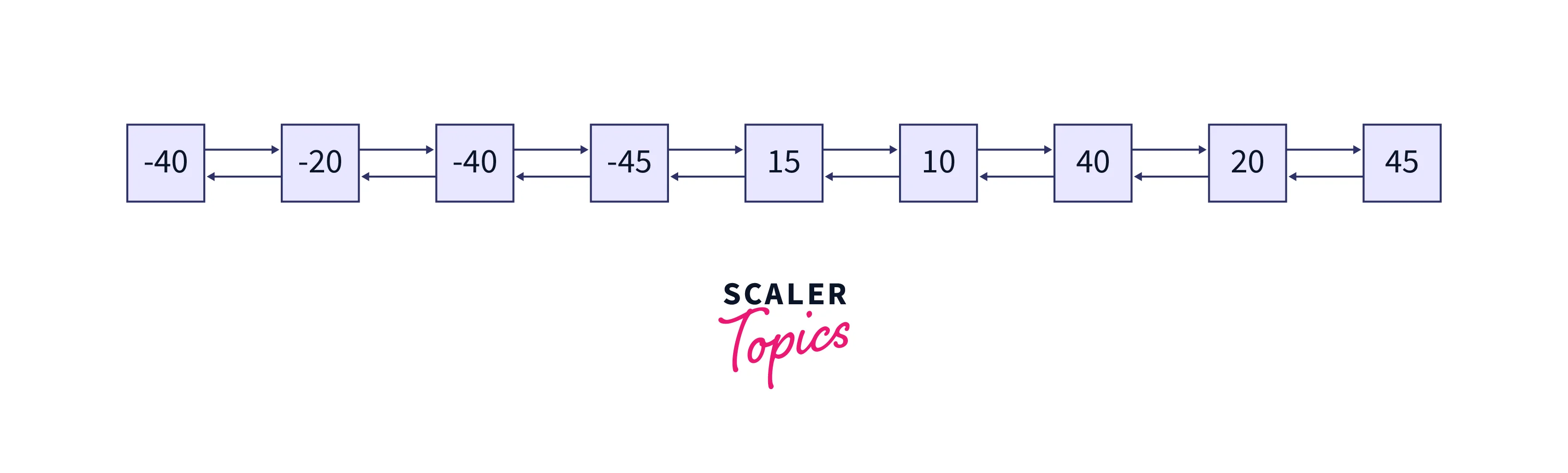
The nodes of the binary tree are converted to the nodes of the doubly linked list. These nodes' values are printed as the output. The doubly linked list formed is shown in the below image:

Complexity Analysis

Time Complexity: $O(N)$, where N is the number of nodes present in the given binary tree.

• Every node of the binary is traversed once during the Inorder traversal, therefore to convert the binary tree into a doubly linked list the overall time complexity of this approach is $O(N)$.

Space Complexity: $O(N)$, where N is the number of nodes present in the given binary tree.

• An auxiliary stack space of $O(N)$ is used during recursion to keep track of the visited nodes during the Inorder traversal which is performed on the given tree.

Approach 5: Iterative Approach

All the above approaches deal with recursion, using an Inorder traversal we convert the binary tree to a doubly linked list. Inorder traversal can also be performed iteratively. Iterative Inorder traversal requires a stack data structure for keeping track of the visited nodes and their current level. Every node is inserted into the stack and a depth first traversal is performed to obtain the deepest leaf node first, then the right node, so in this way the tree is traversed in an Inorder fashion. Here the value of the level indicates whether the node's left is processed or node is processed or node's right is processed or not.

Algorithm

The below algorithm clearly explains the iterative Inorder traversal performed on the tree to convert it into a doubly linked list:

• Traversal is performed using the stack data structure of pair type. Firstly initialize the stack of type pair, because it has to store <Node, int> and insert a pair(root node, 0). Using a while loop on the stack, until the stack is empty, perform the below steps:

  • Pop the top element from the stack and extract its node and level separately.
  • If the level is 3 or the node's value is Null, this is the base and we can move to the next top element in the stack.
  • If that's not the case then push the [root, level+1] into the stack.
  • Now, we need to check whether the extracted level has the value of 0, it indicates that we need to process the left side of the node. If the level is 0 whenever just push the node's left and level=0 [node.left, 0] into the stack.
  • If the level is 1, then we need to process the node in it by converting it into a node of the doubly linked list. Check whether the prev is None, if the prev pointer is null and the flag is true, it indicates the present node is the first node in the doubly linked list and makes this the head of the doubly linked list. Change the value of the flag indicating the head of a doubly linked list is already discovered.
  • If the level is 2, it indicates that the present node's left is processed, the node's data is also processed and we need to process the right tree of the node, so we need to push [node.right, 0] into the stack.

• Whenever the level is 0, it means it that the node is processed for the first time. Where as level 1 indicates it's the second time it is traversed, so we try to process it.

Implementation

Below is the implementation of the approach which is discussed above for converting the given binary tree to the doubly linked list:

C++ implementation for converting the given binary tree to the doubly linked list by processing subtrees:

Python implementation for converting the given binary tree to the doubly linked list by processing subtrees:

Java implementation for converting the given binary tree to the doubly linked list by processing subtrees:

Output:

Explanation:

We can observe that the order of the doubly linked list is the same as the Inorder traversal on the given binary tree. The input binary tree is shown in the below image.

The nodes of the binary tree are converted to the nodes of the doubly linked list. These nodes' values are printed as the output. The doubly linked list formed is shown in the below image:

Complexity Analysis

Time Complexity: $O(N)$, where N is the number of nodes present in the given binary tree.

• Every node of the binary is traversed twice once to convert it into the doubly linked list, if the level of the node in the stack is 0, it is again pushed into the stack by incrementing the level, so every node is traversed twice.
• Therefore the overall time complexity of this approach is $O(N+ N)$.

Space Complexity: $O(N)$, where N is the number of nodes present in the given binary tree.

• Extra space is needed during the iterative Inorder traversal on the given binary tree which uses stack data structure for keeping track of the nodes.
• The maximum number of elements in a stack is N, therefore the space complexity is $O(N)$.