What is Bipartite Graph?

A bipartite graph (also referred to as a bigraph), is a graph whose vertices can be segregated into two disjoint sets such that no two vertices in the same set have an edge between them. They are equivalent to two-colorable graphs (a graph that can be colored with two colors such that no two adjacent vertices are of the same color).

What is a Bipartite Graph?

A bipartite graph has vertices which can be divided into two independent sets (say $P$ and $Q$) such that every edge $u\rightarrow v$ connects a vertex from the set $P$ to a vertex in set $Q$ or vice-versa. In other words, set $P$ and $Q$ are disjoint sets $i.e.$ $P\cap U=\phi$. Due to this property, there must not exist any edge $u\rightarrow v$ such that $u$ and $v$ belong to the same set.

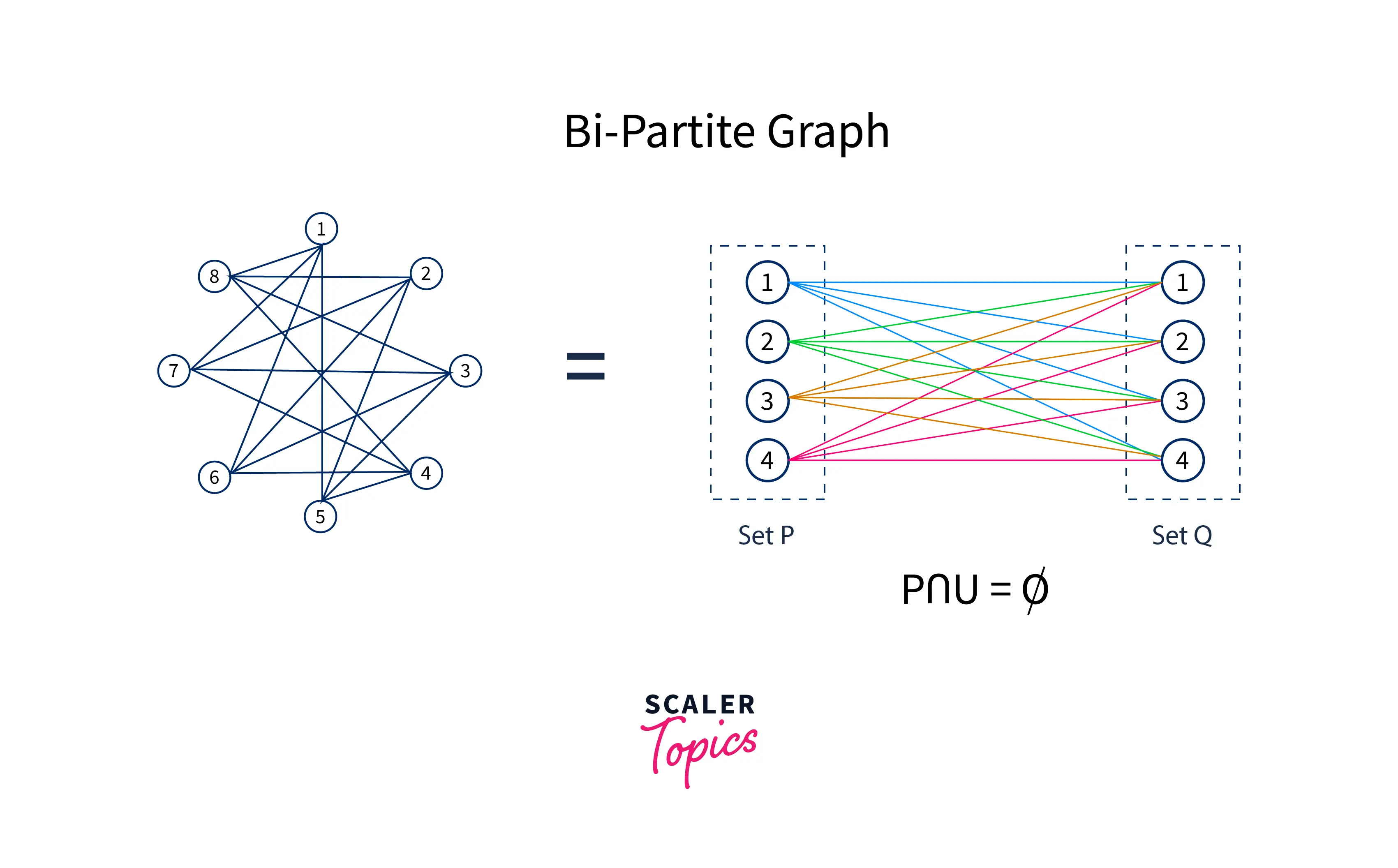
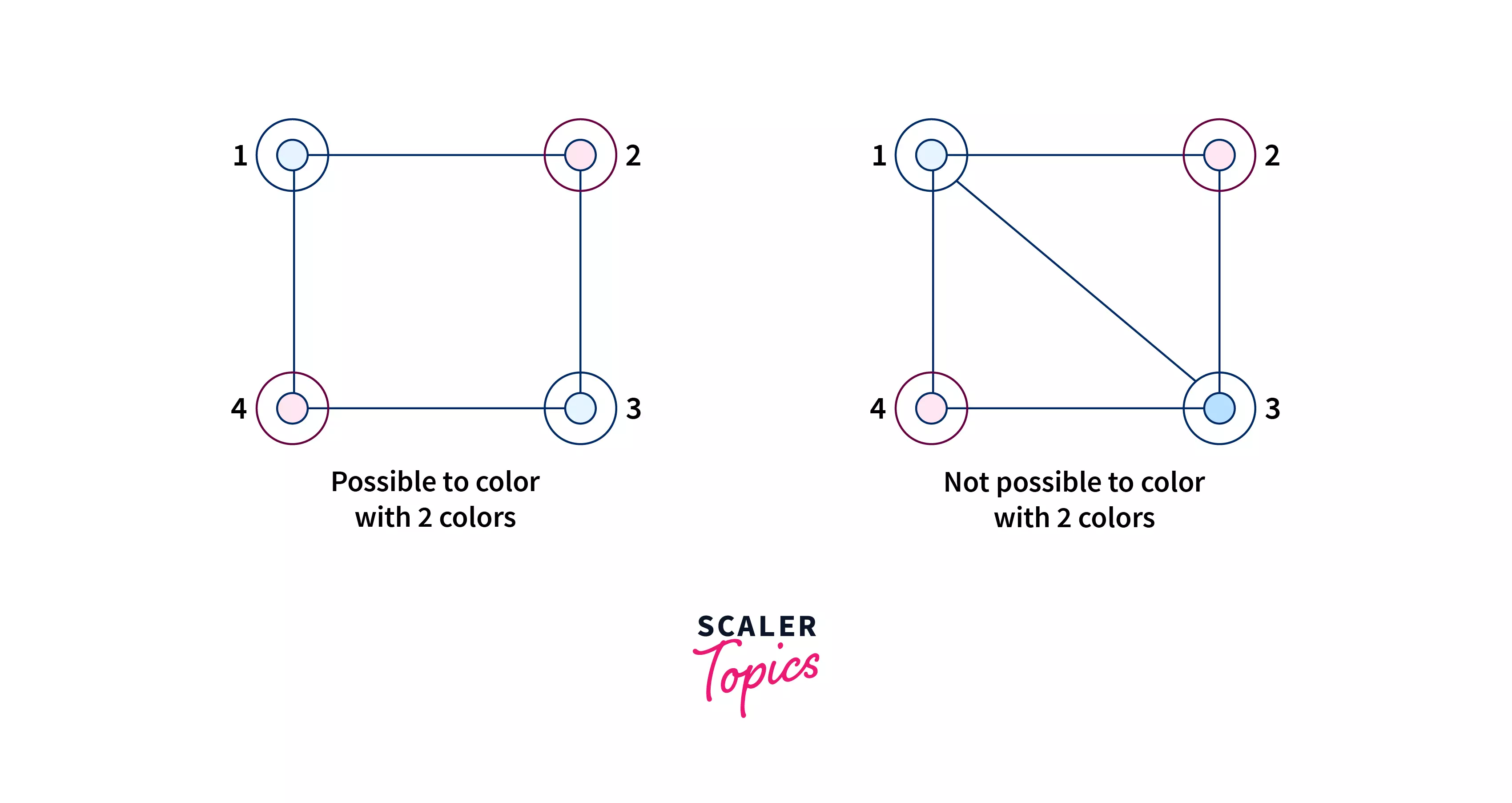
If a graph is bipartite then it is possible to color all of its vertices using two colors, such that no two adjacent vertices have the same color.

For example:

Bipartite Graph Example

It can be seen that the set of all the vertices on the left-hand side has no edge between them and the set of all the vertices on the right-hand side has no edge between them. Hence, this graph fulfills all the conditions of the Bipartite graph.

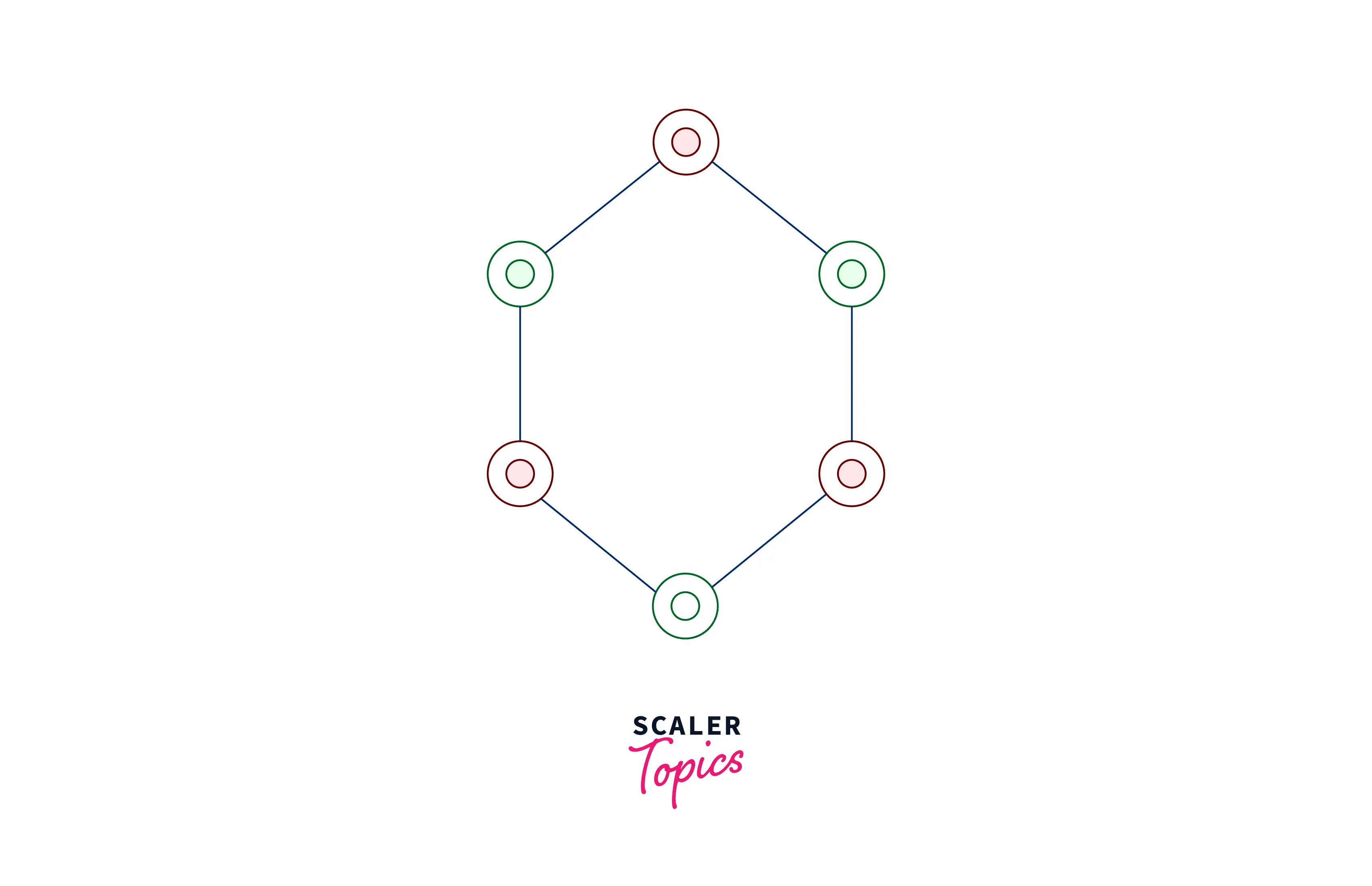
It can be seen that all the vertices of the graph are colored using two colors $i.e.$ red and green such that no two adjacent vertices are of the same color. Hence this qualifies for the bipartite graph.

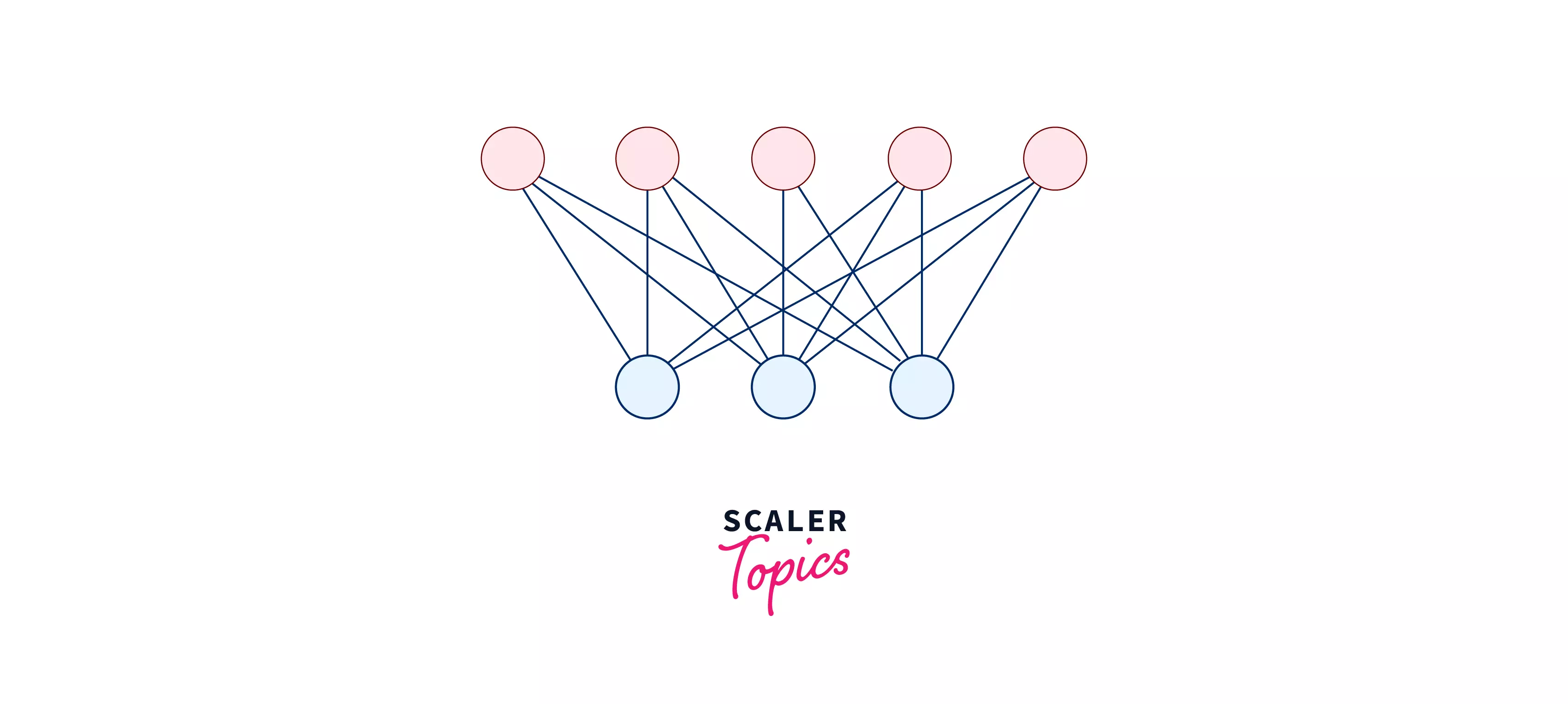
Similarly, this graph can also be colored using two colors, hence this is also a bipartite graph.

Algorithm to Check if a Graph is Bipartite or Not?

It is possible to check whether a graph is bipartite or not either by using the DFS or the BFS. Here, we will see the BFS approach. Let's say we have a graph $G=(V, E)$, where $V$ is the number of vertices, and $E$ is the number of edges. The idea is to make an array (say color) of character type, which will be used to store the color assigned to $i^{th}$ vertex, and then start traversing the graph starting from any of the vertex in the range $[0, V-1]$.

The algorithm is as follows -

• Define the character array color, and initialize all its values by U. Here U denotes that the vertices are uncolored.

• Now define a Queue (say q) which is used to perform a breadth first search traversal.

• Push vertex 0 in the q, and assign a color to it (say R). Here, R denotes red color.

• Now, iterate while the q is not empty and do the following -

  • Deque the vertex from q and store the value in an integer (say u).
  • Iterate for all the adjacent vertices (say v) of u and to the following -
    • If v has already been colored with color[u], it means the graph can't be colored with two colors and hence it is not bipartite.
    • Otherwise assign the complementary color of the color[u] to v $i.e.$ If u is colored with Red, assign the green color to v or vice-versa.

• If we have not encountered any two vertices colored with the same color it means the graph is bipartite.

Dry Run

Let's dry run this approach on the given graph -

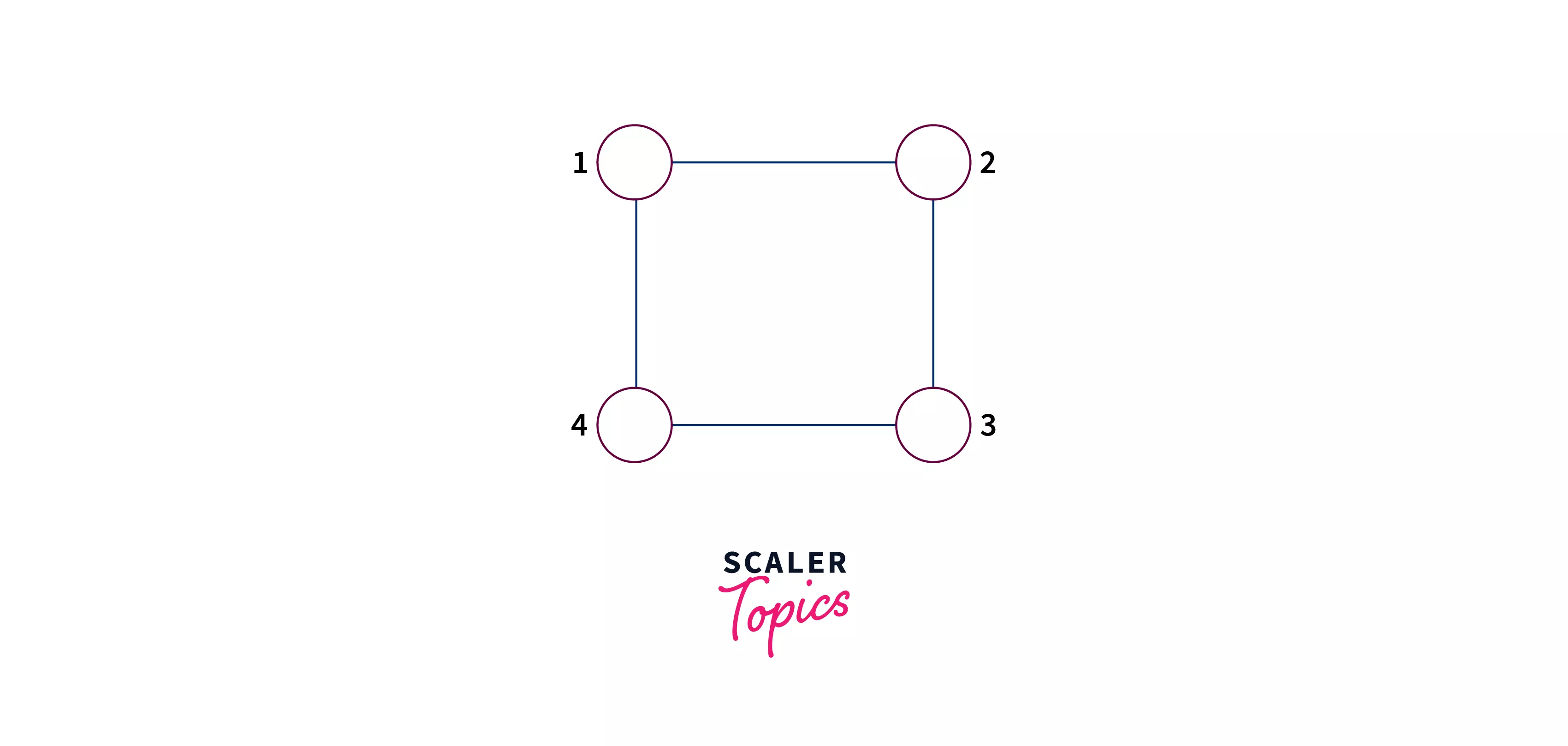
• As the first step, we will create an array (say color) of size $V$ which is 4, and assign U to all of them to denote that all of them are uncolored. Note that we will be following 1-based indexing for this whole dry run. So, we have color[] = {U, U, U, U}
• Now we will define q and push the first vertex (here 1) in the q and color it with Red color. Therefore after this step, we will have
  • color[] = {R, U, U, U}
  • q = [1]
• Now as per the algorithm we will iterate till q is not empty and do the following -
  • Iteration 1 -
    • Dequeue vertex from q and store in u $i.e.$ u=1
    • Iterate for all the uncolored adjacents of u, push them in the queue and color them with green color (since u is colored red). After this iteration, we will have
    • color[] = {R, G, U, G}
    • q = [2, 4]
  • Iteration 2 -
    • Dequeue vertex from q and store in u $i.e.$ u=2
    • Iterate for all the uncolored adjacents of u, push them in the queue and color them with red color (since u is colored green). After this iteration, we will have
    • color[] = {R, G, R, G}
    • q = [4]
  • Iteration 3 -

    • Dequeue vertex from q and store in u $i.e.$ u=3

    • Iterate for all the uncolored adjacents of u, push them in the queue and color them with red color (since u is colored green). But as it can be noticed, now there are no uncolored adjacent vertices of 3. After this iteration, we will have

    • color[] = {R, G, R, G}

    • q = []

  • The Queue is empty now, and we have not seen any violation of the bipartite graph property therefore we can conclude that the graph is a bipartite graph.

Java Implementation

Output -

C++ Implementation

Output -

Python Implementation

Output -

Complexity Analysis

• Time Complexity - Since we are performing a BFS traversal, we visit each vertex once. Hence, the time complexity is O(V+E) if the graph is represented using an adjacency list, and O(V*V) if the graph is represented using an adjacency matrix.
• Space Complexity - No matter how the graph is represented, the space complexity is the same as that of the BFS algorithm i.e. O(V), which is due to the auxiliary array of size V.

Applications of Bipartite Graph

Bipartite graphs find diverse applications across various domains, including:

1. Matching Problems: Bipartite graphs offer an effective modeling tool for addressing matching problems, such as pairing job seekers with job vacancies or assigning students to project supervisors.

2. Social Networks: Bipartite graphs can represent user interactions, with one set of nodes denoting users and the other set representing interests, groups, or communities.

3. Web Search Engine: The query and click-through data of a web search engine can be aptly characterized using a bipartite graph, where one set of vertices represents queries and the other set corresponds to web pages.

Practice Problems

Problem 1 -

Question - Let's say you have $n$ vertices and you want to construct a bipartite graph from them, what is the maximum number of edges you can have in the graph.

Answer - $\lfloor{\frac{n^2}{4}}\rfloor$

Explanation -

The optimal way to achieve the most number of edges is to keep $\frac{n}{2}$ edges in the left set (say $P$) and remaining in the right set (say $Q$).

For example -

1. $n=5$ $|P| = \frac{5}{2}=2$ $|Q| = 5 - |P| = 3$ Now for each vertex in $P$ we can have $|Q|$ edges. Therefore edges are $2*3 = 6$ which is equal to $\lfloor{\frac{5^2}{4}}\rfloor$.

2. $n=6$ $|P| = \frac{6}{2}=3$ $|Q| = 6 - |P| = 3$ Now for each vertex in $P$ we can have $|Q|$ edges. Therefore edges are $3*3 = 9$ which is equal to $\lfloor{\frac{6^2}{4}}\rfloor$.

Problem 2 -

Question - Check if the graph given in the image below is bipartite or not and if it is partite find the vertices present in two different sets.

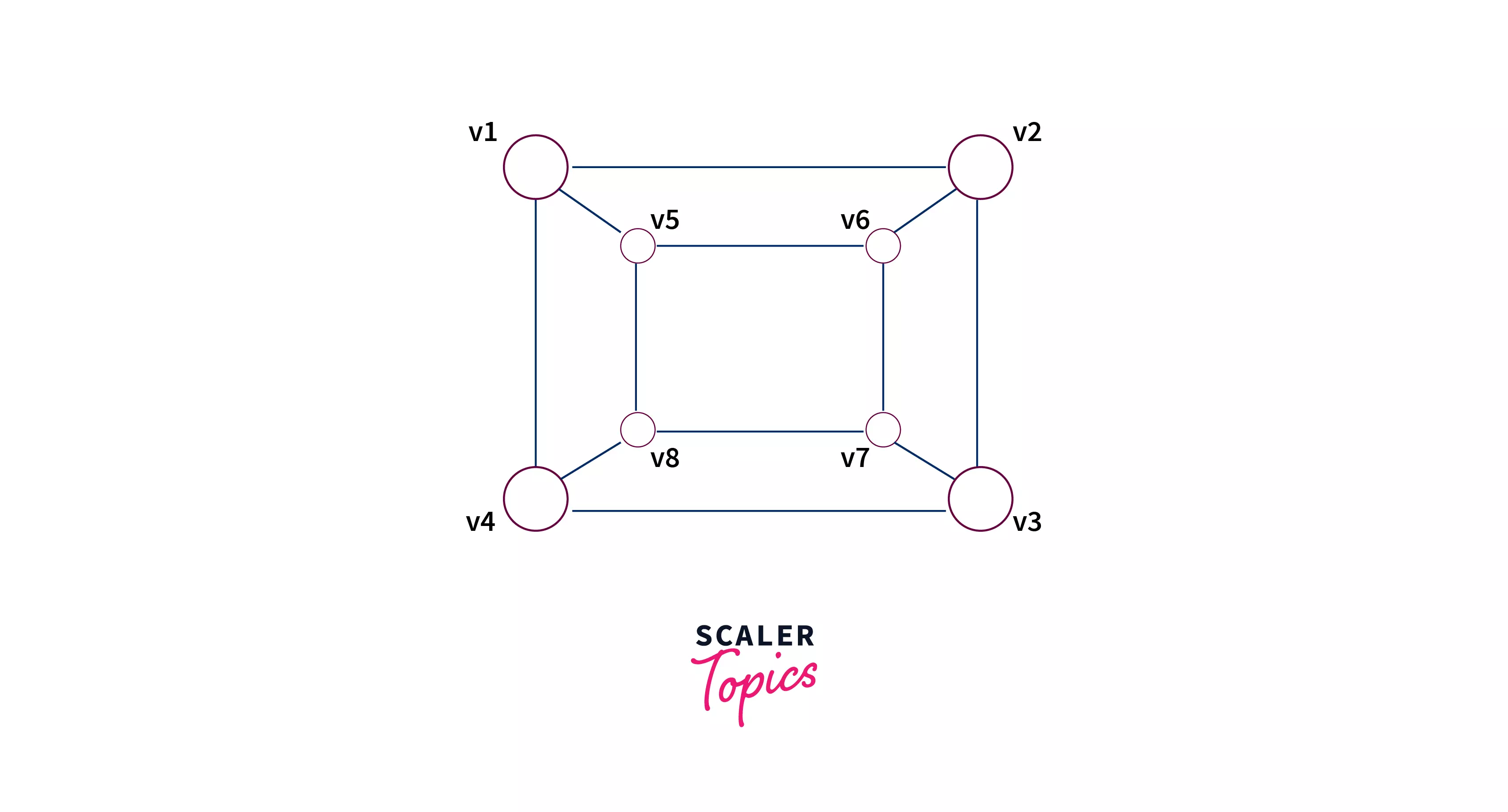
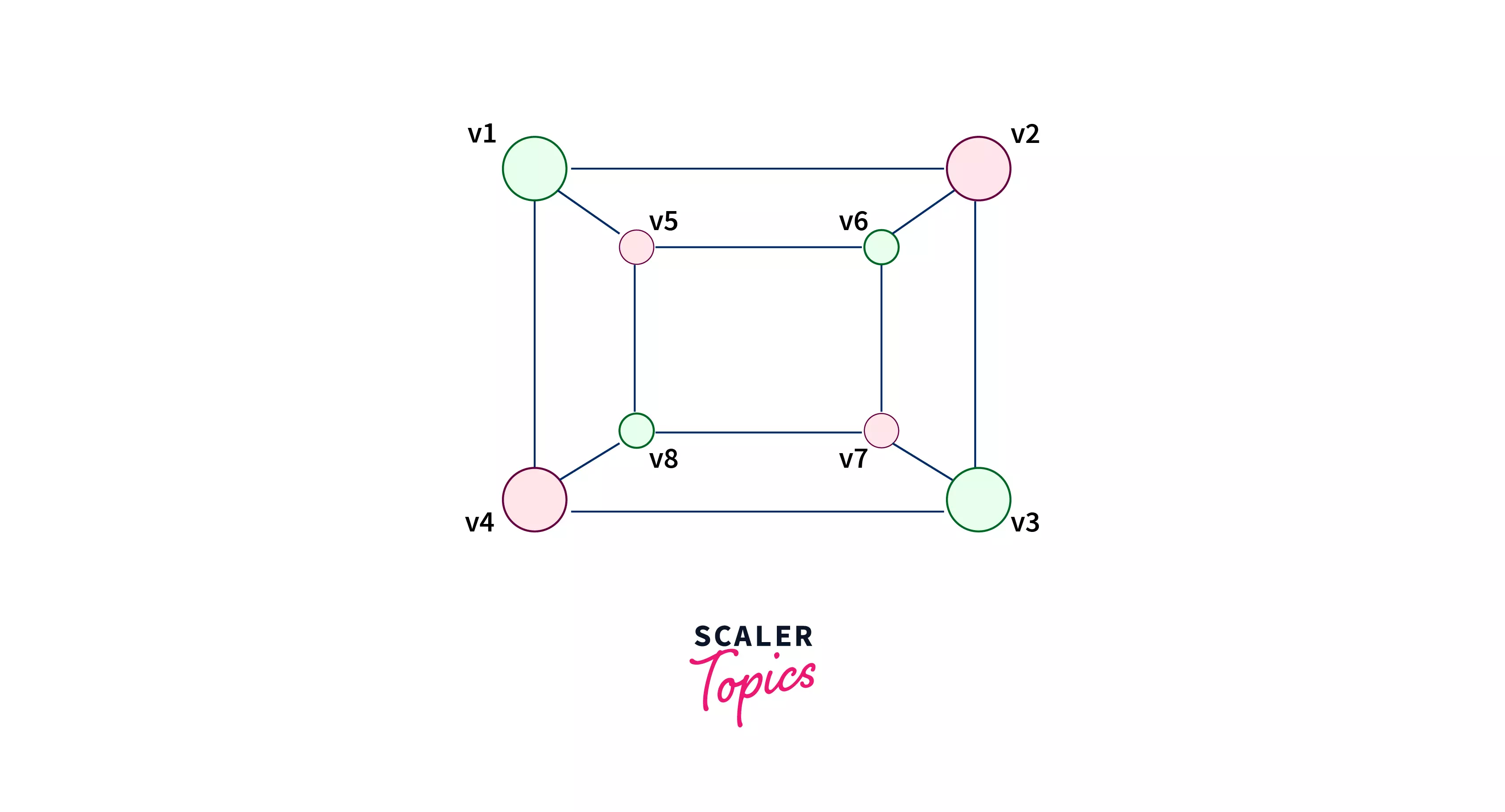
Answer - YES it is bipartite, Vertices in set $P = {v_1, v_3, v_6, v_8}$ and in the set $Q = {v_2, v_4, v_5, v_7}$

Explanation - The graph can be colored in the following manner, and as you can see the vertices which are green in color are in set $P$, while those colored red are in set $Q$.