Boundary Traversal of Binary Tree

Problem Statement

A binary tree will be given in the problem and we need to find the boundary traversal of that binary tree. Boundary traversal of a binary tree means traversing the binary tree along the boundary. The boundary includes the left boundary, right boundary and leaf nodes. Therefore in the boundary traversal of binary trees we will first include the left boundary then leaf nodes and then right boundary.

Important Terms in Boundary Traversal of Binary Tree

In order to solve the above problem we need to know certain terms like:

• The left boundary is the path from the root to the left most node.
• Right boundary is the path from the root to the right most node.
• Leftmost node is a leaf node that we can reach by traversing the left subtree first everytime, if it exists. If there is no left subtree then we go to the right subtree. This we do until we reach the leaf node. This leaf node is known as the rightmost node.
• Similarly we can get the rightmost most node by traversing the right subtree in the above given manner.

Example

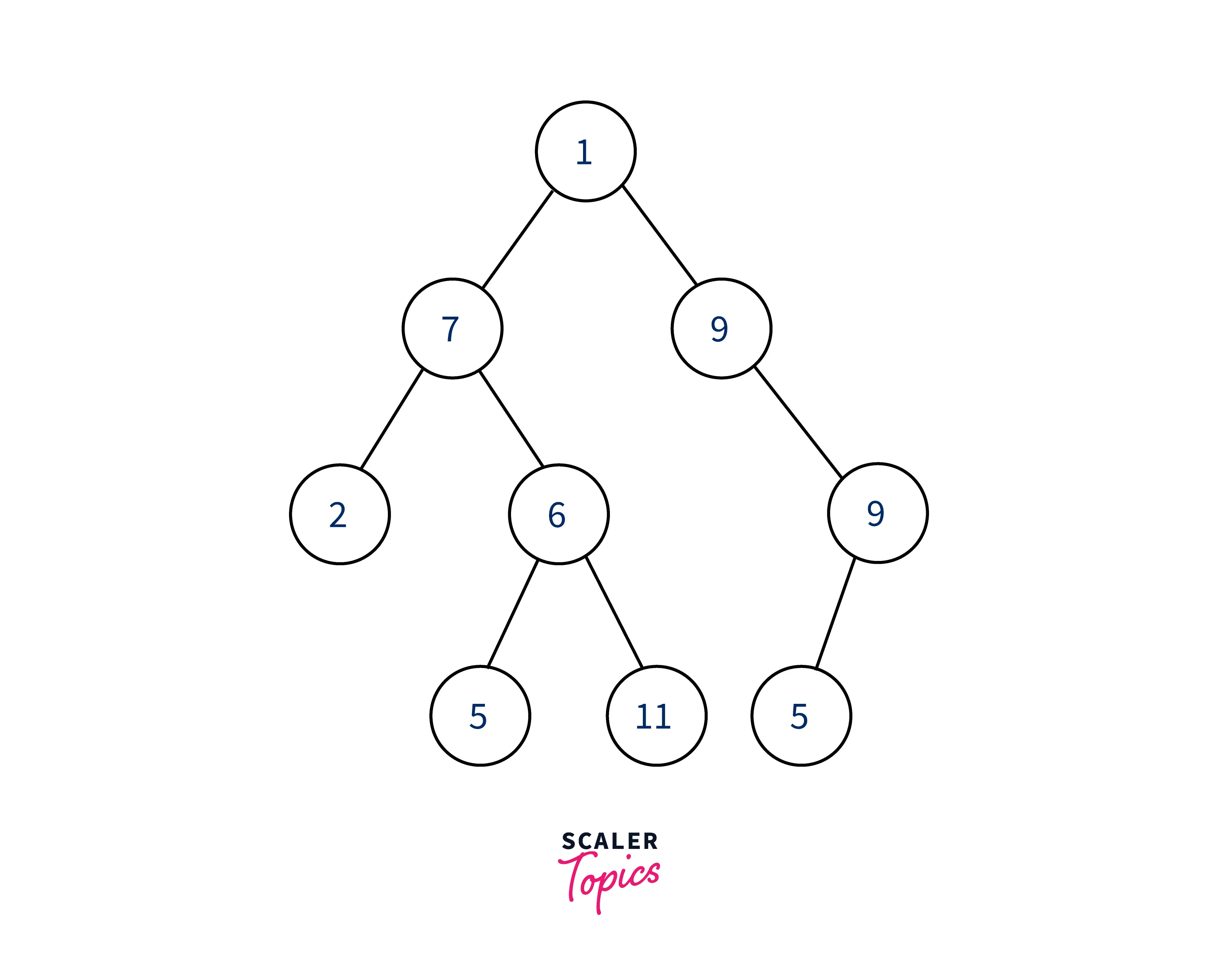
Input

Output

Example Explanation

We need to find the boundary traversal of binary tree given above, we will do it in following manner:

• Visit root (1)
• Path to leftmost node (7,2)
• Leafs nodes (5,11,5)
• Path to rightmost node (9,9)

Thus the boundary traversal of the binary tree becomes : ( 1, 7, 2, 5, 11, 5, 9, 9)

Constraints

• $1 <= n <=$ $10^5$
• $-10^4$ <= node.val $<= 10^4$

Approach 1: Traversing the Boundary in Three Parts: Left Boundary, Leaf Nodes, and Right Boundary

The approach to find the boundary traversal of binary tree is simple and can be done by following these three steps :

• Traverse the left boundary in a top down manner, that is we start from the root and then we go towards the leaf node. In this step we keep traversing the tree until we reach the leftmost node.
• Then we traverse all the leaf nodes from left to right. That is, from the leftmost node we move towards the right and only print the leaf nodes.
• Lastly we traverse the right boundary in a bottom up manner, that is we start from the rightmost node and go towards the root node by following the right boundary path.

Code for Boundary Traversal of Binary Tree

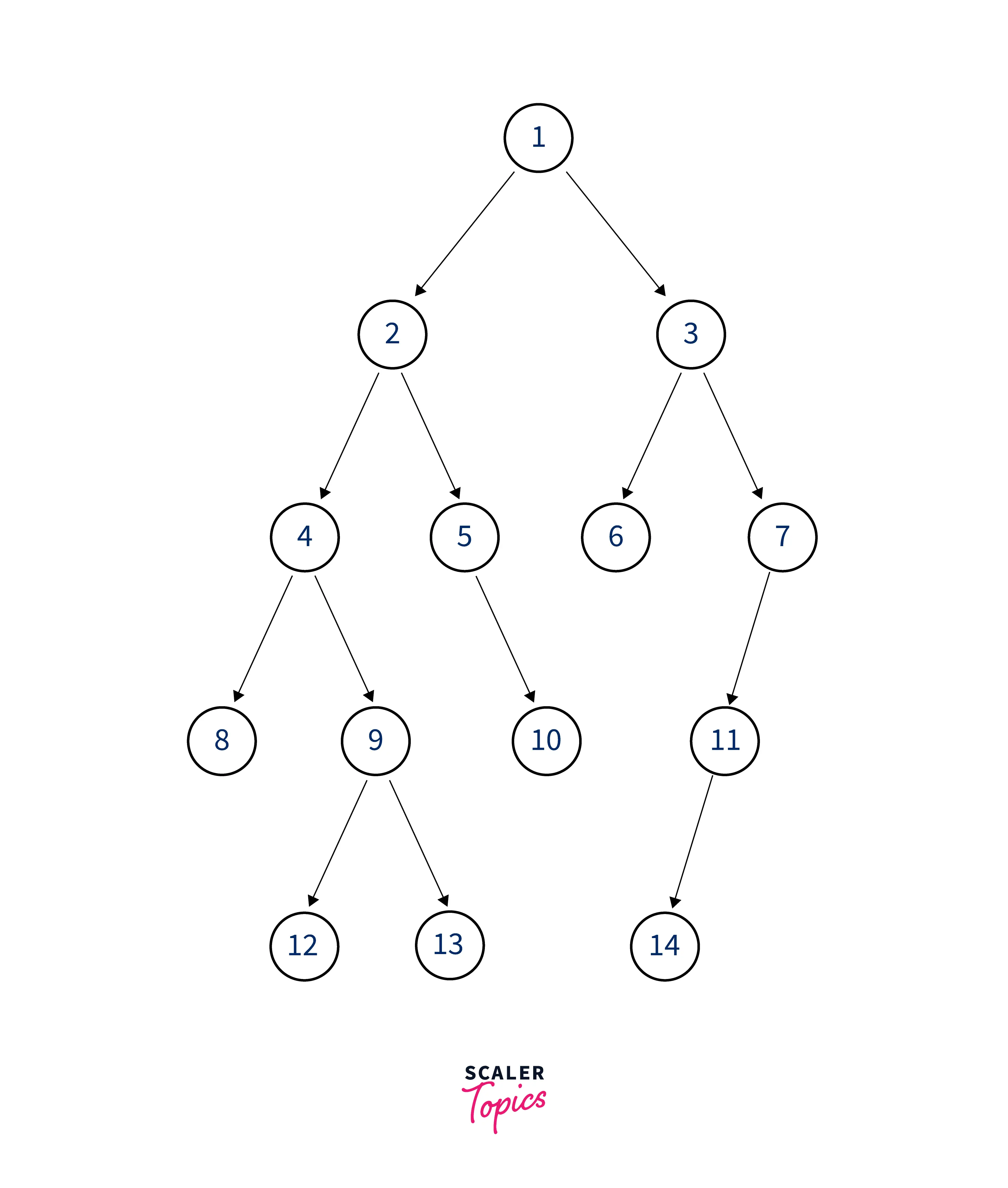
Let's look into the code of boundary traversal of a binary tree. We will create the given below binary tree in the code and then we will find its boundary traversal.

C++ Code implementation

Java Code Implementation

Python Code Implementation

Output :

As discussed above, we will find boundary traversal of binary tree in three steps:

The left boundary in top down manner that is, 1,2,4,8 The leaf nodes from left to right that is, 12,13,10,6, 14 And finally the right boundary in bottom up manner , that is, 11,7,3

Thus the final output for boundary traversal of binary tree is: 1 2 4 8 12 13 10 6 14 11 7 3

Time complexity: O(n), n is the number of nodes in the tree. Since we are traversing each node at most once thus the worst case time complexity in this case would be the time taken to traverse each node once.
Space Complexity: O(h), h is the height of a tree.Because at any time the maximum number of nodes in the recursion call stack would be the height of the tree.