Boundary Value Analysis in Software Testing
Overview
Boundary Value Analysis is a testing technique crucial for software quality assurance, targeting input boundaries to uncover hidden defects. It is particularly adept at detecting precision errors like floating-point rounding issues. By assessing values close to input limits, BVA reveals system vulnerabilities that conventional testing might miss. This method is vital in identifying cases where input values surpass or fall short of system-defined limits. BVA's focus on both upper and lower boundaries enhances software robustness, reducing the risk of unexpected crashes and failures due to boundary-related anomalies.
What is Boundary Value Analysis?
In Boundary Value Analysis, test cases are designed to include values that are on the lower and upper limits of valid input ranges, as well as values just outside those limits. The reason behind this is that errors often emerge at these critical points due to factors like rounding, truncation, or conditional logic.
The main steps in Boundary Value Analysis are:
- Identify the input ranges or conditions for the software component being tested.
- Determine the boundary values for these input ranges (minimum and maximum).
- Design test cases that include the boundary values, values just below the boundaries, and values just above the boundaries.
- Execute the test cases and observe the behavior of the system.
- Analyze the results to identify any errors or unexpected behaviors near the boundaries.
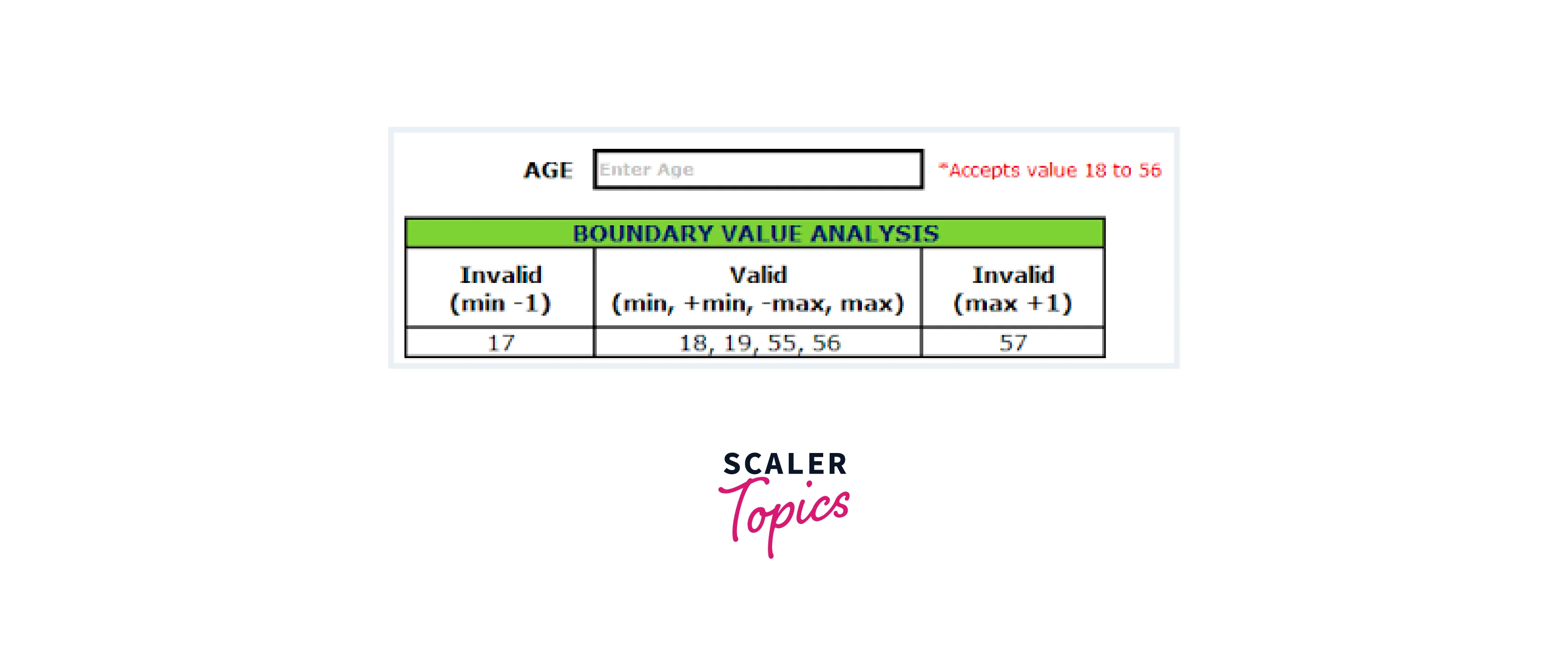
Explain the Test Case of Boundary Value Testing
For instance, consider a scenario where a software component accepts an input within the range of 1 to 100. Boundary Value Testing would involve testing the following values:
- Test Case 1: Test the minimum boundary value (1).
- Test Case 2: Test a value just above the minimum boundary (2).
- Test Case 3: Test a value just below the maximum boundary (99).
- Test Case 4: Test the maximum boundary value (100).
- Test Case 5: Test a value just beyond the maximum boundary (101).
This approach helps identify issues that might arise due to rounding errors, off-by-one errors, or other problems associated with boundary conditions.
Here's a table illustrating the test cases for the given example:
| Input Value | Expected Behavior |
|---|---|
| 1 | Valid |
| 2 | Valid |
| 99 | Valid |
| 100 | Valid |
| 101 | Invalid |
By focusing on these critical values, Boundary Value Testing enhances the thoroughness of testing and aids in improving the software's reliability and robustness.
Single Fault Assumption
The Single Fault Assumption simplifies analysis by considering only one fault or failure at a time in a system. It aids in understanding consequences, isolating causes, and designing countermeasures. While valuable for safety and risk assessments, it overlooks complex interactions of multiple faults that can occur simultaneously, potentially leading to an incomplete understanding of system behavior. Engineers must balance its use with real-world complexities for accurate risk evaluation and mitigation.
The Focus of BVA
- Edge Cases: BVA targets testing scenarios at the edges or boundaries of input ranges.
- Boundary Values: It examines values at the minimum and maximum limits of valid input ranges.
- Adjacent Values: BVA includes values just inside and just outside the boundaries for testing.
- Defect Detection: The technique aims to uncover errors and defects near these critical points.
- Off-by-One Errors: BVA helps identify issues caused by incorrect handling of adjacent values.
- Rounding and Precision Issues: It exposes problems that can arise due to rounding or truncation.
- Overflow and Underflow: BVA detects cases where values might exceed or fall short of limits.
- Enhanced Coverage: By focusing on boundaries, BVA extends test coverage effectively.
- Improved Reliability: Testing at critical points enhances software robustness and reliability.
- Critical for Safety: In safety-critical systems, BVA is crucial for identifying boundary-related vulnerabilities.
Equivalence Partitioning
Equivalence Partitioning is a software testing technique that involves categorizing input values into groups or partitions to simplify test case design. It allows you to test representative values from each section, reducing the number of test cases needed while still effectively covering a range of scenarios.
Example: User Registration Form
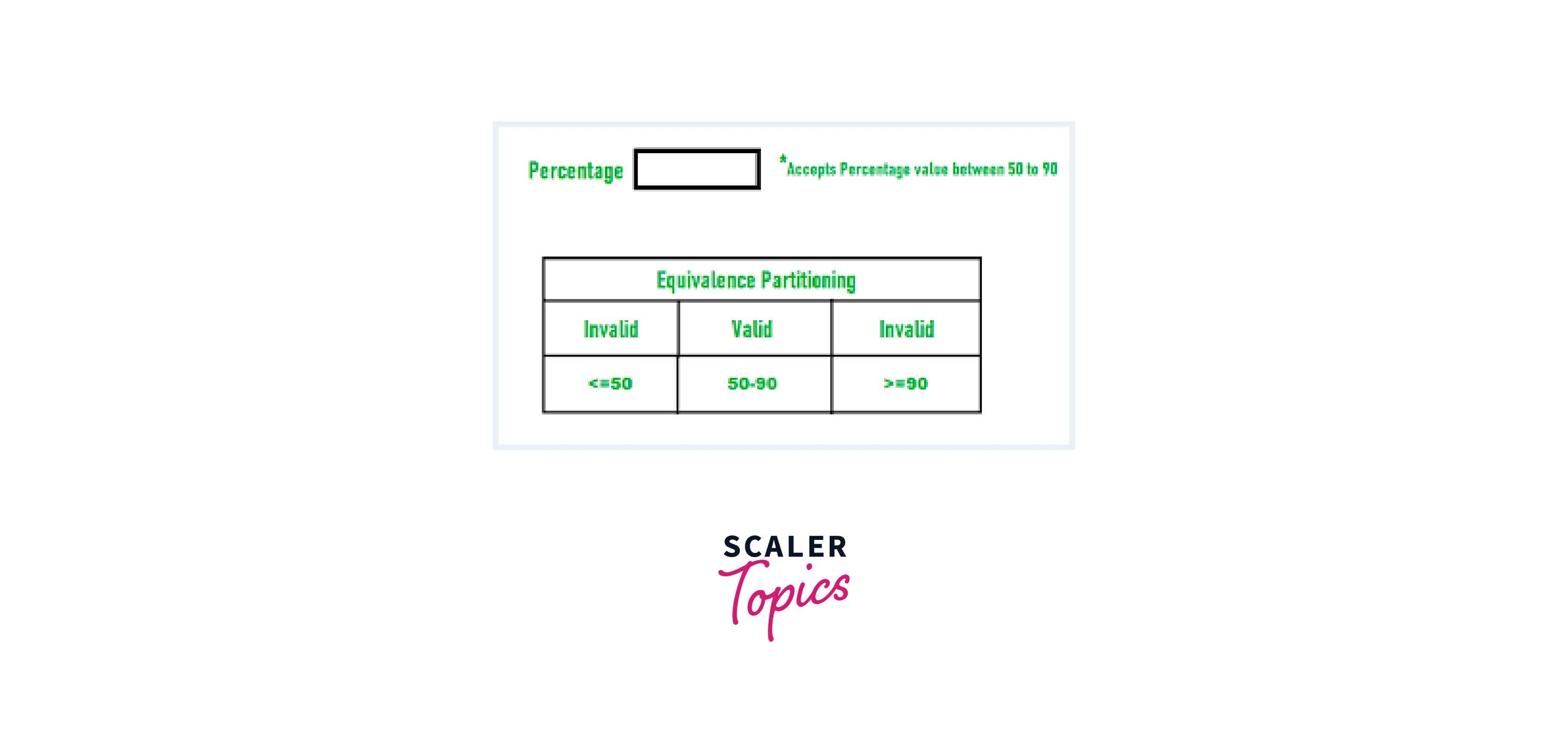
Imagine you are testing a user registration form for a website. One of the fields is "Age," and it should accept values between 18 and 60. Here's how Equivalence Partitioning can be applied:
- Invalid Age (Below 18): Any age below 18 is considered invalid.
- Valid Age (Between 18 and 60): Any age between 18 and 60 is considered valid.
- Invalid Age (Above 60): Any age above 60 is considered invalid.
Using these partitions, you can select representative values for testing. You might choose values that are on the boundaries of each partition as well as values within the partitions:
- Test Case 1: Age = 15 (Invalid)
- Test Case 2: Age = 18 (Valid)
- Test Case 3: Age = 30 (Valid)
- Test Case 4: Age = 60 (Valid)
- Test Case 5: Age = 65 (Invalid)
Why Equivalence & Boundary Analysis Testing?
-
Comprehensive Coverage:
Equivalence Partitioning divides input values into classes expected to exhibit similar behavior. This reduces the number of test cases needed while still covering a wide range of scenarios. BVA, on the other hand, focuses on testing values at the boundaries of these partitions. Together, they ensure comprehensive coverage of critical scenarios.
-
Error Detection:
Equivalence Partitioning helps in detecting general errors within partitions, while BVA is particularly effective at exposing errors related to boundary conditions. Combining both techniques increases the likelihood of discovering defects that might be overlooked by using only one method.
-
Efficiency:
Using Equivalence Partitioning helps in efficient test case design by selecting representative values from each partition. BVA then takes this efficiency further by concentrating on boundary values, which often have a higher chance of causing issues.
-
Minimizing Redundancy:
Equivalence Partitioning reduces redundancy by testing values that share similar characteristics. BVA complements this by ensuring that values at partition boundaries are thoroughly tested, minimizing the chances of boundary-related errors.
-
Structured Approach:
Both techniques provide a structured approach to test case design. Equivalence Partitioning helps categorize values logically, while BVA ensures that critical boundary values are tested rigorously.
-
Risk Mitigation:
By combining these techniques, you're targeting both general behavior and critical edge cases. This mitigates the risks associated with software defects more comprehensively.
-
Industry Best Practices:
Equivalence Partitioning and BVA are well-established and widely adopted testing techniques in the industry. Many testing standards and methodologies recommend using them for their effectiveness.
Limitation of Boundary Value Analysis
- BVA might not cover all possible scenarios and combinations of inputs.
- It assumes errors are more likely near boundaries, which might not always be accurate.
- BVA's concentration on boundary conditions may overlook various defect types, leading to potential gaps in test coverage.
- It's less effective for non-numeric inputs without clear boundaries.
- BVA might miss other defect types like functional or logical errors.
- Complex systems might have multiple boundaries that are challenging to cover comprehensively.
- Overemphasis on boundaries might lead to neglecting other crucial testing areas.
Conclusion
- BVA is a valuable technique to improve software reliability by targeting critical boundary scenarios, and uncovering off-by-one errors, rounding issues, and boundary-related defects.
- BVA helps in targeted testing at points most likely to exhibit anomalies, optimizing testing efforts.
- It complements Equivalence Partitioning and other techniques, providing comprehensive coverage, widely recognized and adopted in software testing standards and methodologies.
- BVA reduces the number of test cases by focusing on critical values, saving time and resources by Detecting errors at the boundaries can prevent defects from propagating deeper into the system.
