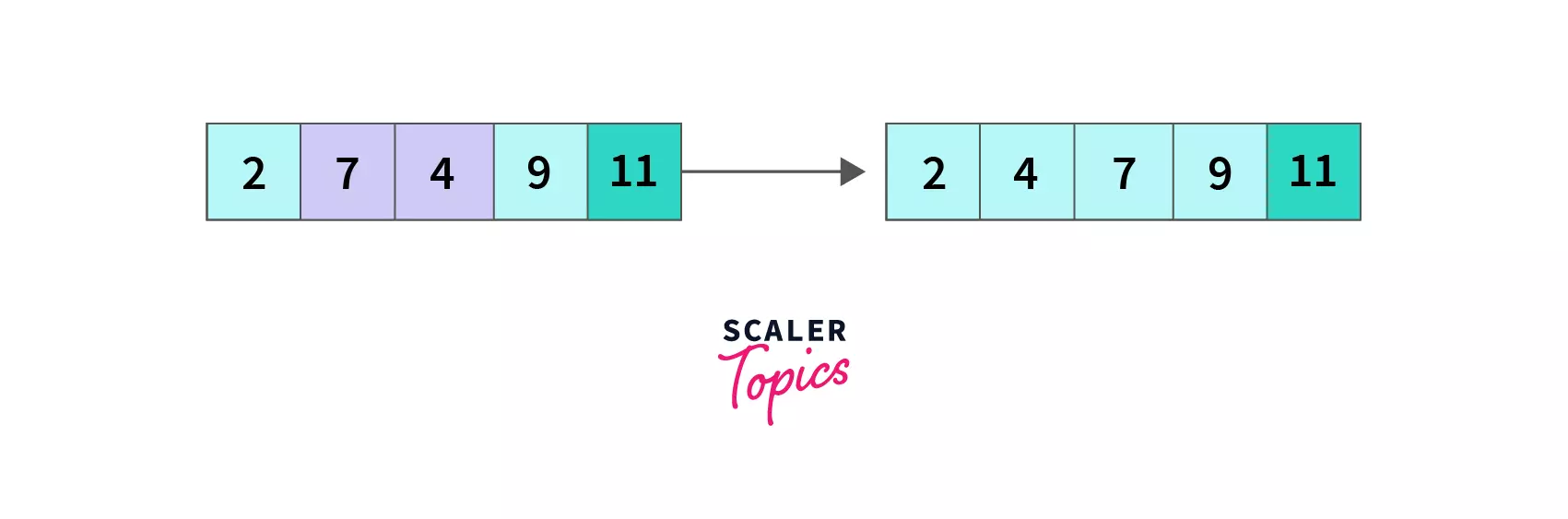
Bubble Sort in Java

Algorithm for Bubble Sort in Java

Using the bubble sort algorithm, we can sort an unsorted array A of size N in increasing order in three simple steps. Traverse the array N-1 times and follow the steps.

1. Starting with the very first element of the array, compare the current element with the next consecutive element.
2. If the current element A[i] is greater than the next element A[i+1], swap them, move to the next element, and repeat step 2.
3. Otherwise, move to the next element and repeat step 2.

Bubble Sort Example

Let's take an unsorted array A = [7,11,9,2,4] containing five elements. We will sort it in increasing order using the Bubble sort in Java. Our desired output is [2,4,7,9,11].

To sort the array, we need a total of 4 (N-1) passes indexed from 0 to 3.

Let's walk through the algorithm step by step.

First pass (PassNum = 0)

• index = 0, we compare A[0] and A[1] since 7 < 11, so there is no change in the array, and we move to the next element.

  • 

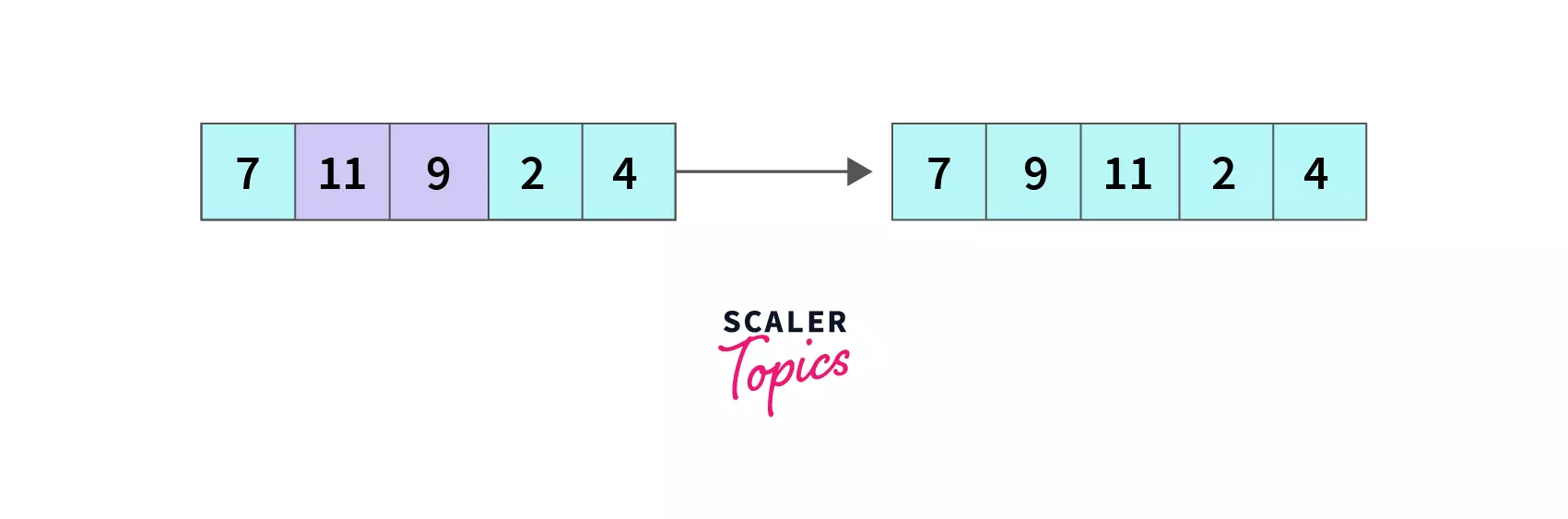
• index = 1, A[1] which is 11 is greater than A[2] which is 9 so we swap A[1] and A[2], the array becomes [7,9,11,2,4] and we move to the next element.

  • 

• index = 2, compare A[2] with A[3], 11 > 2 so A[2] and A[3] are swapped and the array becomes [7,9,2,11,4] and we move to next element.

  • 

• index = 3, compare A[3] with A[4], 11 > 4 so A[3] and A[4] switch their places resulting the array as [7,9,2,4,11].

  • 

  End of the first pass, we compared all five elements in pairs by iterating till the second last element, and as a result, 11 is pushed to its desired position, and the array is [7,9,2,4,11] now.

Second pass (PassNum = 1)

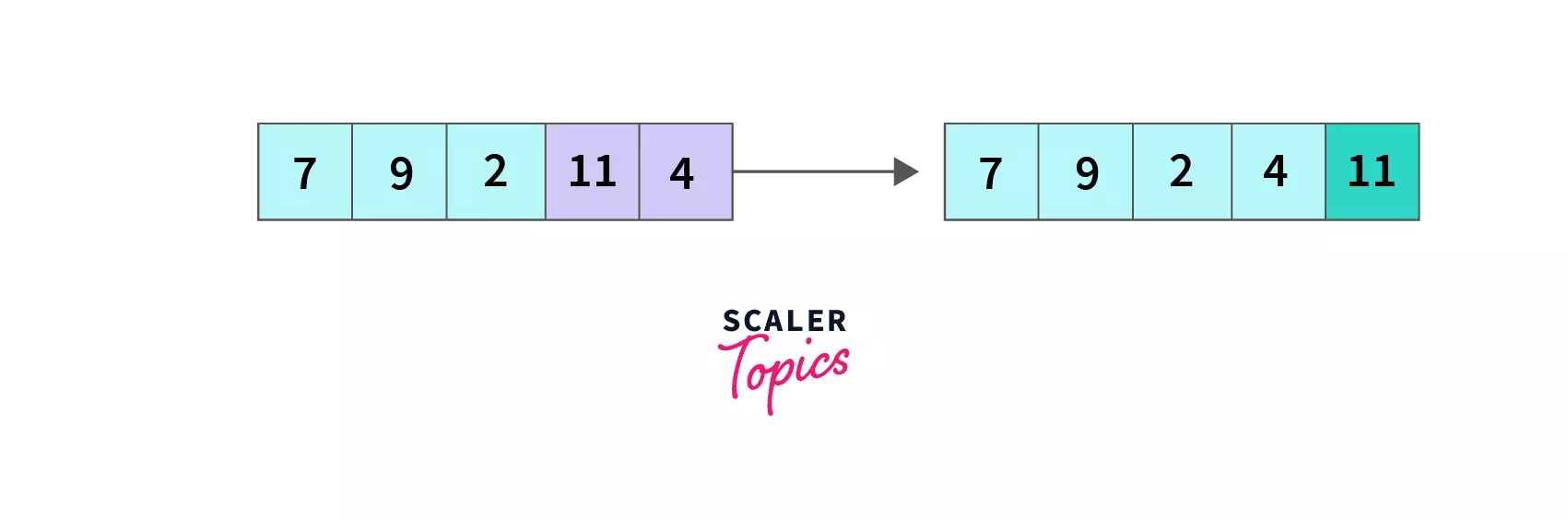
• index = 0, we compare A[0] and A[1], since 7 < 9, so there is no change in the array, we move to the next element.

  • 

• index = 1, A[1] is 9 is greater than A[2] is 2 so we swap A[1] and A[2], the array becomes [7,2,9,4,11] and we move to the next element.

  • 

• index = 2, compare A[2] with A[3], 9 > 4 so A[2] and A[3] are swapped and the array becomes [7,2,4,9,11].

  • 

  At the end of the second pass, we compared all four remaining unsorted elements (11 were sorted in the first pass) in pairs by iterating until the second last element. As a result, 9 (the largest of the remaining 4 elements) is pushed to its desired position, and the array is [7,2,4,9,11] now.

Third pass (PassNum = 2)

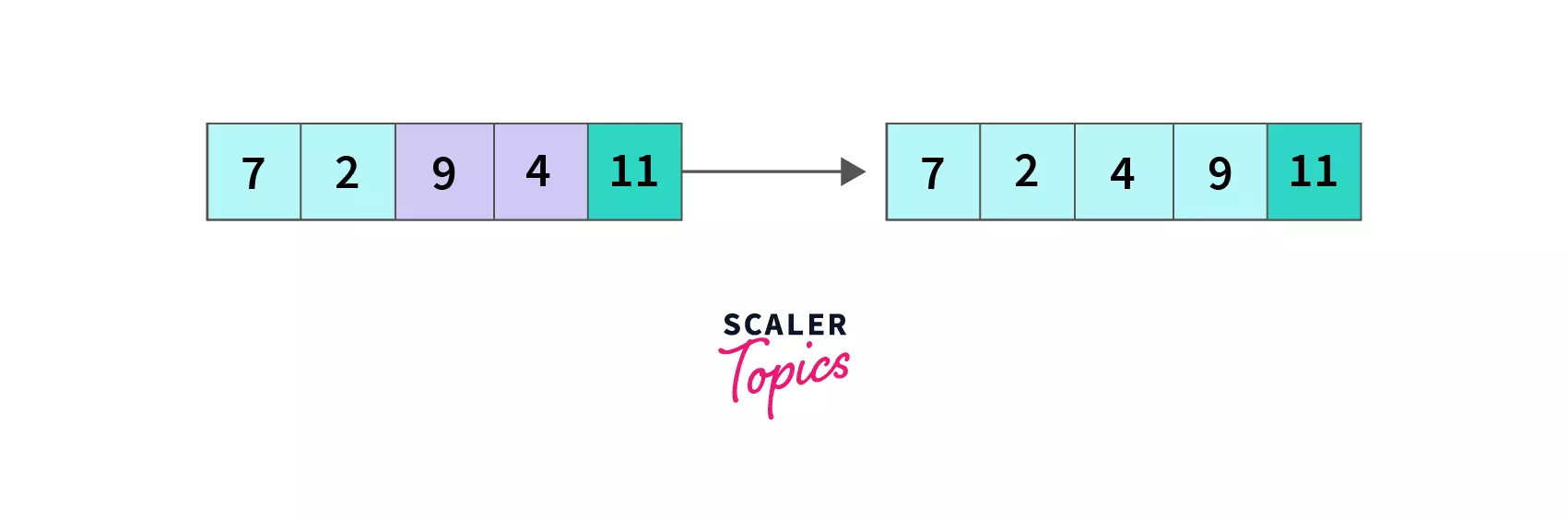
• index = 0, A[0] which is 7 is greater than A[1] that is 2 so we swap A[0] and A[1], the array becomes [2,7,4,9,11] and we move to the next element.

  • 

• index = 1, compare A[1] with A[2], 7 > 4 so A[2] and A[3] are swapped and the array becomes [2,4,7,9,11].

  • 

  At the end of the third pass, we have compared all three remaining unsorted elements (9 and 11 were sorted earlier) in pairs by iterating until the second last element. As a result, 7 (the largest of the remaining three elements) is pushed to its desired position, and the array is [2,4,7,9,11] now.

Fourth pass (PassNum = 3)

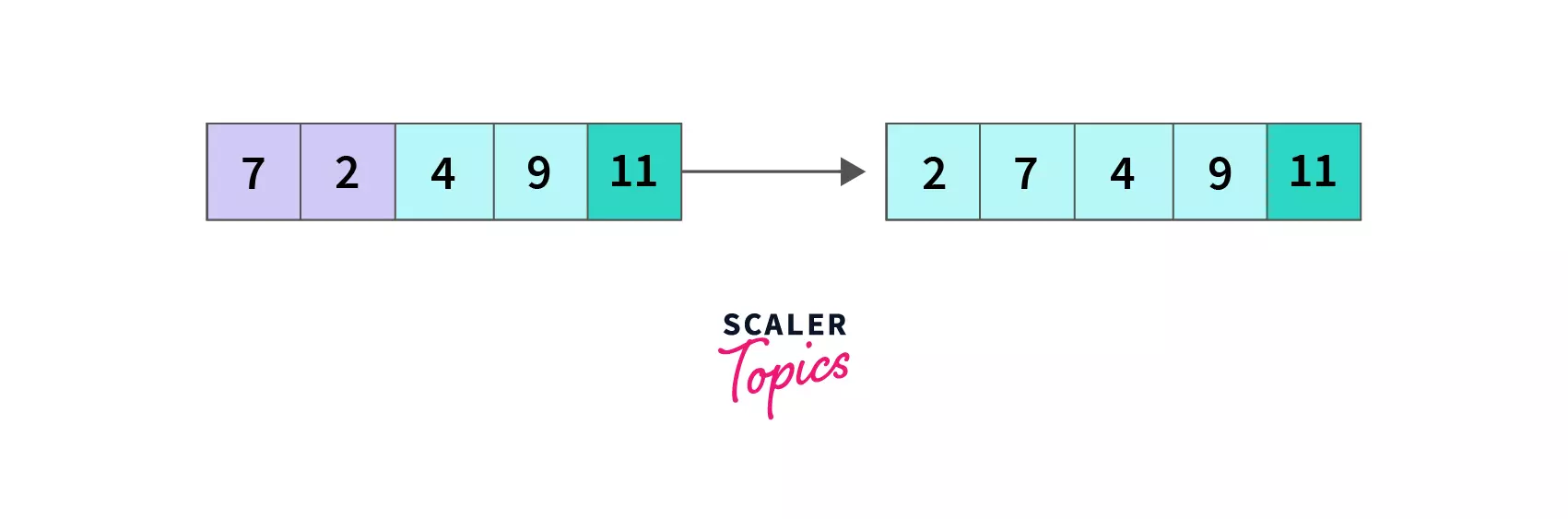
• index = 0, we compare A[0] and A[1], since 2 < 4, so no change in the array.

  • 

  At the end of the fourth pass, even though the array was sorted in the third pass, we don't have a way to check if it's sorted and end the loop. As a result, we had to complete the maximum number of N-1 passes possible.

Implementation of Bubble Sort in Java

The below Java program is the implementation of a bubble given unsorted array A of length N.

Complexity Analysis

Time complexity:

• Worst Case: O($N^2$)
• Best Case: O(N)

Space Complexity:

• O(1)

Advantage of Bubble Sort in Java

• The bubble sort's main advantage is that it is widely used and simple to implement.
• In its best-case scenario, which checks whether the array is already sorted, the optimized algorithm is highly efficient.
• Bubble sort is an in-place sorting technique, which means it does not require additional space to sort the array; it can modify the original array.