C Program to Find Area of Triangle

We all have drawn and calculated the areas of different shapes like rectangle, circle, triangle, etc., in school. It was so fun doing that, but sometimes it also gets heavy on the calculation side when we have to calculate with decimals or when we are working with large numbers. So why not write a program to calculate the area?

Introduction

The area of a shape is calculated by measuring how much space it occupies if kept on a plane. We have formulas to calculate the areas of different shapes. Using those formulas, we will write programs to calculate the areas using different approaches.

In this article, we will mainly focus on calculating a triangle's area in C language.

C Program to find Area of Triangle using its Coordinates

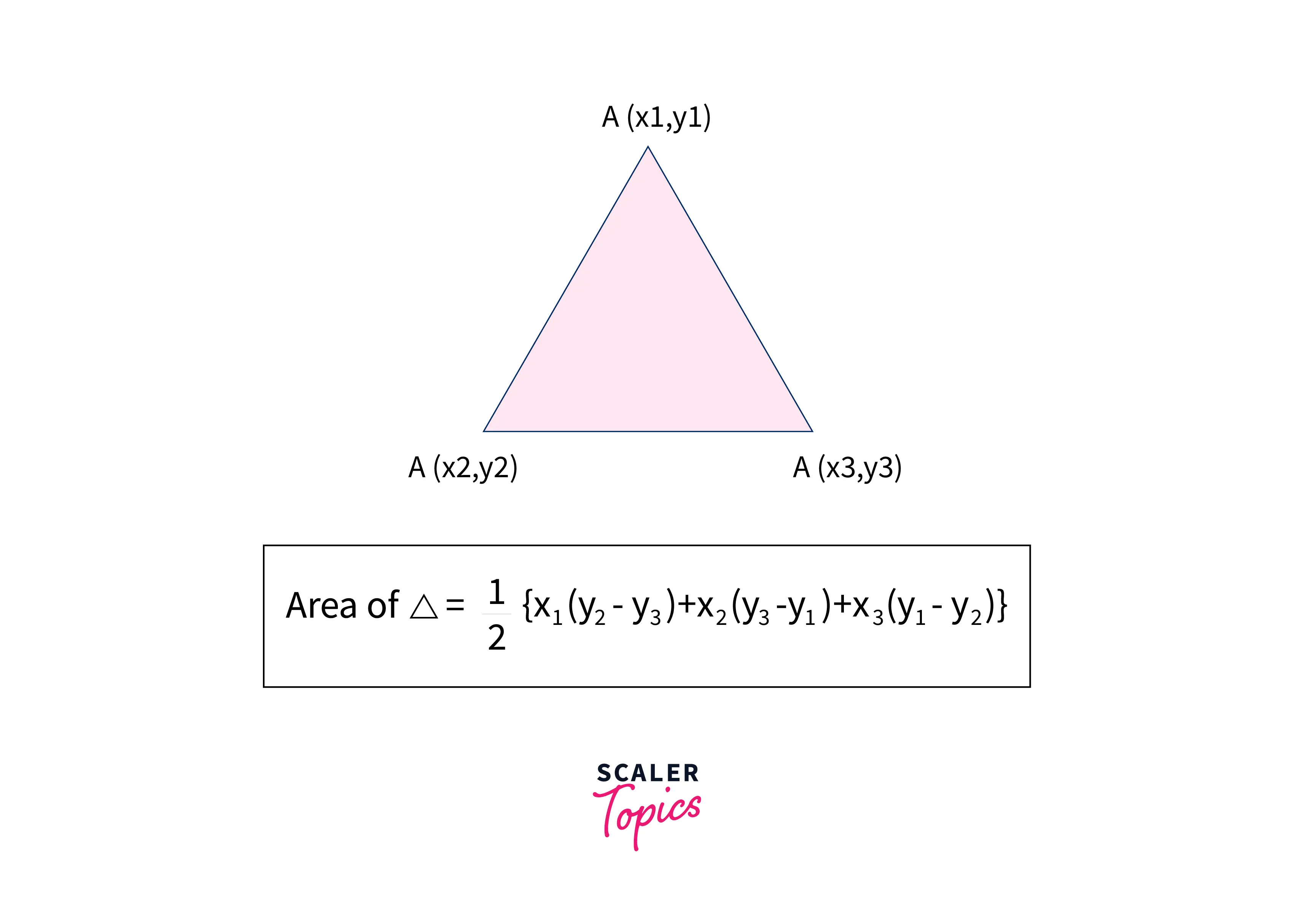
In this method, we will have three coordinates representing the position of all three vertices of a triangle on the Cartesian plane.

We will be following a straightforward approach. As we know, the formula to find the area of a triangle having coordinates as

{(x1, y1), (x2, y2), (x3, y3)} is

${Area = } {1\over 2} {|x1(y2-y3) + x2(y3-y1) + x3(y1-y2)|}$

We have to write a program to convert this logic into code, so let's begin.

Program to find area of a triangle in c language

Output:

area of triangle using its coordinates

C Program to find the Area of a Triangle using Base and Height

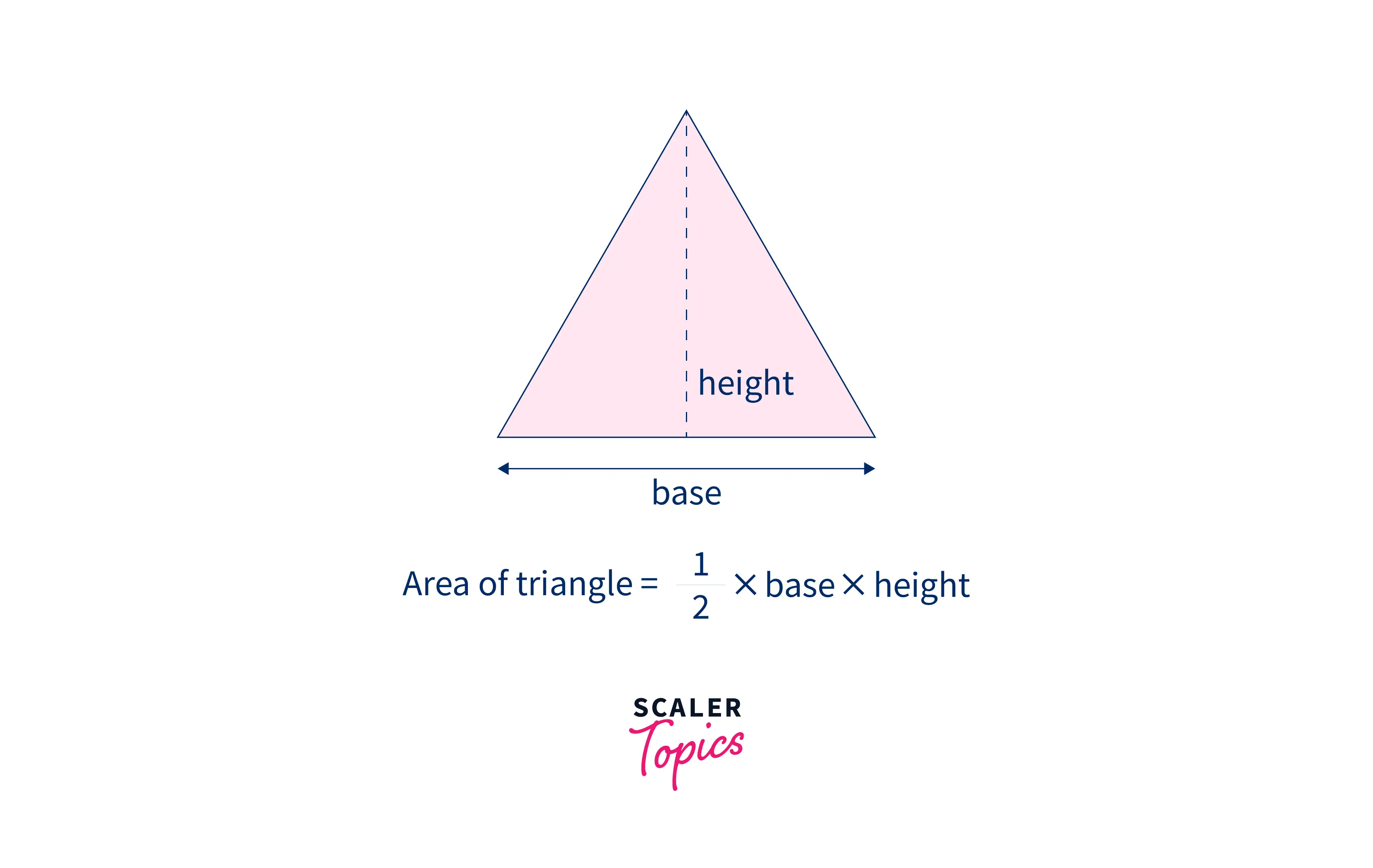
Now, we will be given the base and height of a triangle and asked to find its area. We will again apply the same thing; we know the formula, and all we have to do is write a program using that logic, so let's see it.

We know that if we have the base and height of a triangle, then we can find its area by using

$Area = {1 \over2} * base * height$

Program to find area of a triangle in c language

Output:

Note:

You may have noticed, I have written ((float)1/2) while calculating the area in the both of the above approaches, lets understand the reason for that.

As 1 and 2 both are integers, and any operation on int and int will result in an int, so as soon as 1/2 gets calculated, it will become 0, because internally, yes it will result in 0.5, but as the compiler is instructed to result only an int value if the operation is done between int and int, so it will omit the floating value .5 and will return only 0.

Hence, the whole multiplication will become 0 as $0 * anything = 0$ ,

This is why it is first being typecasted to float so that it can hold the complete 0.5 value and hence will give the accurate result.

area of triangle using base and height

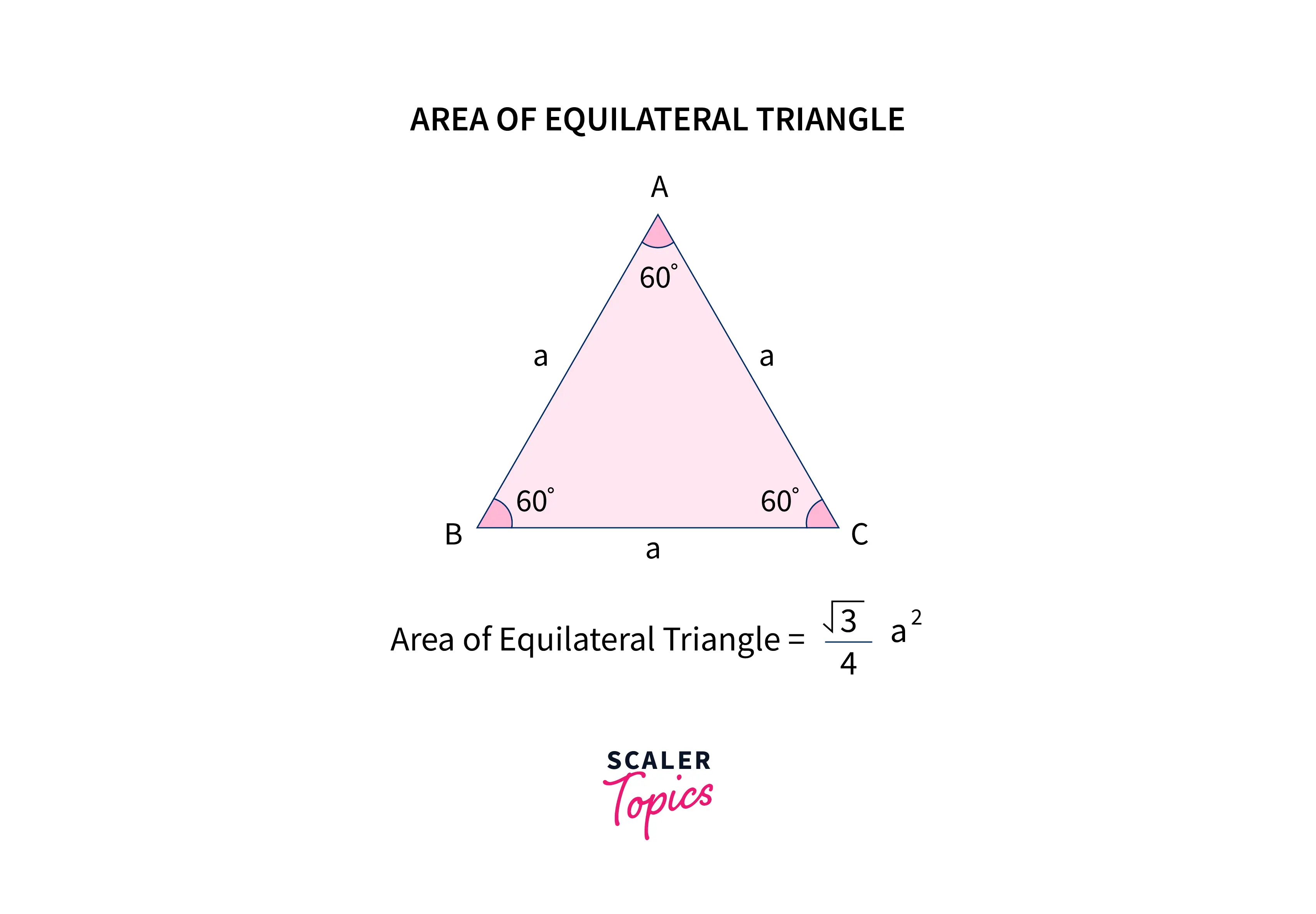
C Program to find the Area of Equilateral Triangle

This is the easiest one; we know that an equilateral triangle is a triangle that has all its sides equal The simple formula to calculate its area is

${Area =} {\sqrt{3}\over4} * side^2$

So, let's begin writing its code.

Program to find area of a triangle in c language

Output:

area of equilateral triangle

C Program to find Area of Triangle using Heron's Formula

This is where we will need more attention, but don't worry, it is not hard. It takes time to be a little more attentive, and we will start easy, so

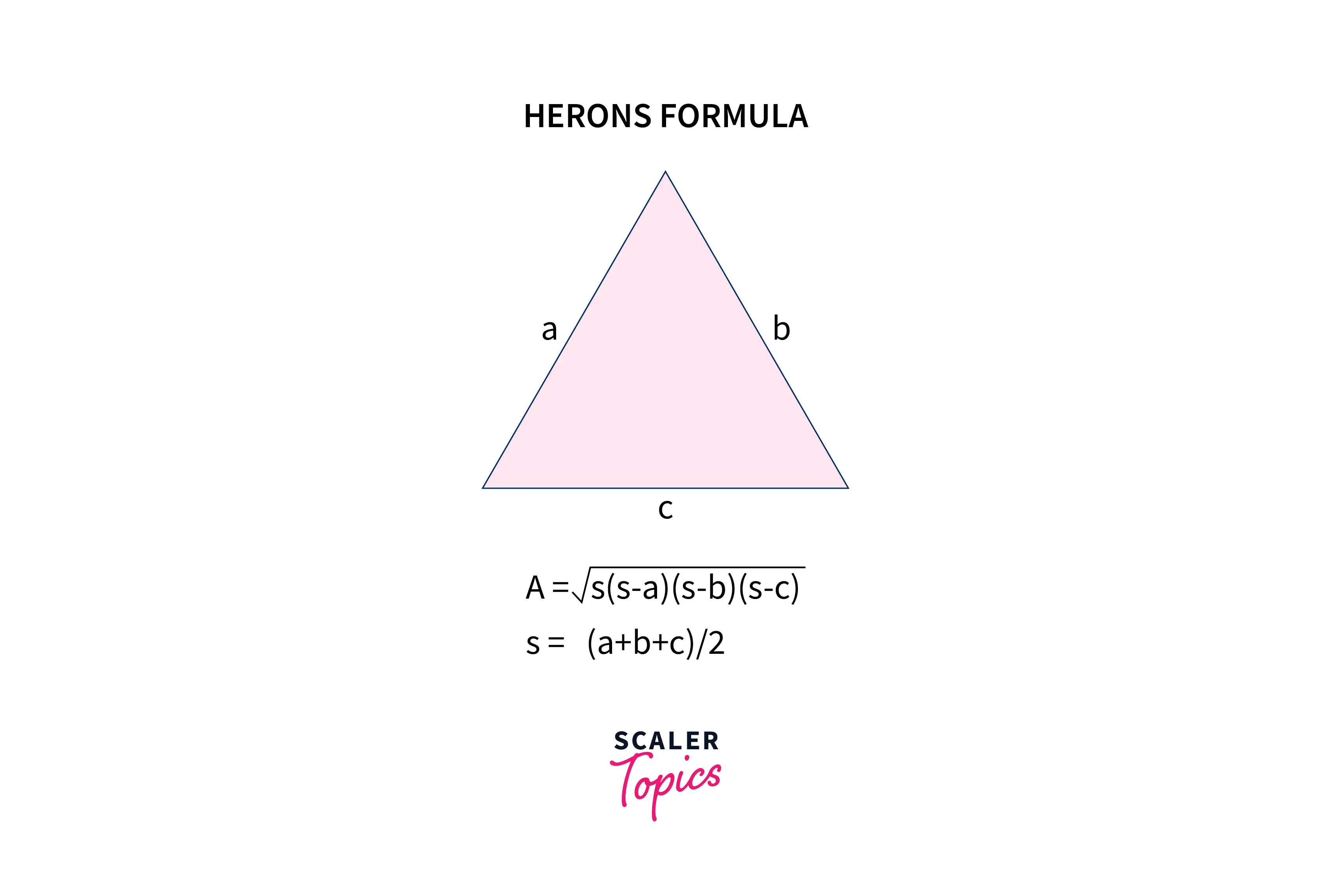
Heron's formula is a formula we can use to calculate the area of almost any triangle. All we need is to have the measurement of all three sides directly, or they should be calculatable. If this happens, then it's just a matter of seconds or minutes to calculate the triangle's area.

Heron's Formula is mainly used to calculate the area of scalene triangles (triangles having all the 3 sides unequal) because we do not have any general formula for them.

So, when the base and height of a scalene triangle are unknown, we can use Heron's formula to calculate its area.

Now, let's look at the formula first.

$Area = {\sqrt{s(s-a)(s-b)(s-c)}}$ $s = {\frac {(a+b+c)}2}$

Here, a, b, c are the sides and s is the semi-perimeter of the triangle.

Let's start writing this into the code.

Program to find area of a triangle in c language

Output:

area of triangle using heron's formula

C Program to find Area of the Triangle using a Function

We have been writing the logic in the main function until now, and that is totally fine if we have to calculate the area only once. Still, if we want to write a scalable program that we can scale in the future, or simply if we will need to find the area multiple times, then it is always a good practice to wrap the logic into a global function and call it every time we need to calculate the area.

Let's write the code for all the programs we have discussed using global functions.

Area of Triangle Using Coordinates:

Area of Triangle Using Base and Height:

Area of Equilateral Triangle using Functions:

Area of Triangle using Heron's Formula:

Conclusion

There are many methods to find the Area of a triangle as per the situation, and accordingly, we can apply the respective formulas
Formula to calculate Area if the coordinates are given ${Area = } {1\over 2} {|x1(y2-y3) + x2(y3-y1) + x3(y1-y2)|}$
Area if base and height are given $Area = {1 \over2} * base * height$
Area of Equilateral Triangle ${Area =} {\sqrt{3}\over4} * side^2$
Area using Heron's Formula $Area = {\sqrt{s(s-a)(s-b)(s-c)}}$ $s = {\frac {(a+b+c)}2}$
Now, we are aware of all the above formulas, so all we have to do is think about the logic of implementing these mathematical formulas into a program and find the area we need.