C Program to Find the Roots of a Quadratic Equation

Quadratic equations, expressed as ax² + bx + c = 0, involve coefficients a, b, c, where a ≠ 0. They have three types of roots—real and distinct, real and equal, or real and imaginary—determined by the discriminant (b² - 4ac). Roots are real and distinct if the discriminant is positive, real and equal if zero, and imaginary if negative.

\begin{aligned} & a x^2+b x+c=0 \\ & x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a} \end{aligned}

Nature of the Roots

As we have seen above the nature of roots is decided by the value of the discriminant, and the discriminant of the quadratic equation is calculated as b²-4*a*c

discriminant(d) = b²-4ac

The nature of the roots is given as,

D = b²-4ac	Nature of roots
D > 0	roots are real and distinct (unequal)
D = 0	roots are real and equal.
D < 0	roots are real and imaginary.

Analysis

If the value of discriminant (b²-4*a*c) is greater than 1, then the value of root1 and root2 of the equation can be calculated as:

root1 = (-b + √d) / 2a root2 = (-b - √d) / 2a

For example, the roots of a quadratic equation x^2 - 7x - 12 are 3 and 4, which are real and distinct.
If the value of discriminant (b²-4*a*c) is equal to 1, then the value of both the roots is -b / 2a.

For example, the roots of x^2 - 2x + 1 are 1 and 1, which are real and equal.
If the value of discriminant (b²-4*a*c) is less than 1, then the value of root1 and root2 of the quadratic equation can be calculated as:

root1 = -b / 2a + i (√d / 2a) root2 = -b / 2a - i (√d / 2a)

For example, the roots of the quadratic x^2 + x + 1, roots are -0.5 + i0.86603 and -0.5 - i0.86603, as we can see roots are real and imaginary.

If the discriminant $>0$ ,

\operatorname{root} 1=\frac{-b+\sqrt{ }\left(b^2-4 a c\right)}{2 a}

\text { root2 }=\frac{-b-\sqrt{ }\left(b^2-4 a c\right)}{2 a}

If the discriminant $=0$ ,

\operatorname{root1}=\operatorname{root} 2=\frac{-b}{2 a}

If the discriminant $<0$ ,

\begin{aligned} & \operatorname{root} 1=\frac{-b}{2 a}+\frac{i \sqrt{ }-\left(b^2-4 a c\right)}{2 a} \end{aligned}

\operatorname{root} 2=\frac{-b}{2 a}-\frac{i \sqrt{ }-\left(b^2-4 a c\right)}{2 a}

Procedure

The procedure for solving a quadratic equation is to combine all of the like terms and move them to one side of the equation. Here, we are factoring an equation by moving all the likely terms to one side of the equation, keeping the x² term positive. To perform this step of combining the terms, we can add or subtract all of the x² terms, the x terms, and the integer terms, moving them to one side of the equation so that nothing remains on the other side.

Once the other side (the right side of an equation after the equal "=" sign) has no remaining terms, you can just write "0" on that side of the equal sign.

Transform Your Career

Choose from our industry-leading programs designed for career success

NSDC Certified

Modern Software and AI Engineering Program

Master full-stack development with AI integration

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Modern Data Science and ML with specialisation in AI

Advanced data science techniques with AI specialization

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Advanced AIML with Specialisation in Agentic AI

Deep dive into AIML with focus on Agentic systems

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

DevOps, Cloud & AI Platform Engineering

Build and manage AI-powered cloud infrastructure

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

AI Engineering Advanced Certification by IIT-Roorkee

Premier AI engineering certification from IIT-Roorkee

3 MonthsDuration

AI-LedCurriculum

Career SupportSupport

Go to Program

Steps to Find the Square Roots of the Quadratic Equation

Initialize all the variables used in the quadratic equation.
Take inputs of all coefficient variables a, b, and c from the user.
Find the value of the discriminant of the quadratic equation using the formula:

Discriminant = (b * b) - (4 * a * c)
Find the roots based on the nature of the discriminant of the quadratic equation.
If the value of discriminant (b²-4ac) is greater than 1, then the value of root1 and root2 of the equation can be calculated as:

root1 = (-b + √d) / 2a root2 = (-b - √d) / 2a
Print the roots that are real and distinct.
Else if the value of discriminant (b²-4ac) is equal to 1, then the value of both the roots is -b / 2a.
Print that both roots are real and equal.
Else if the value of discriminant (b²-4ac) is less than 1, then the value of root1 and root2 of the quadratic equation can be calculated as:

root1 = -b / 2a + i (√d / 2a) root2 = -b / 2a - i (√d / 2a)
Print that both the roots are imaginary.
The first root is (r + i) img and the second root is (r - i) img.
Stop or Exit from the program.

Pseudo Code of the Quadratic Equation

BEGIN
NUMBER a, b, c, d, root1, root2
INPUT a,b,c
d = b^2-4ac
IF (d >= 0) THEN

root1 = (-b+√d)/2a or root1 = (-b+d^(1/2)/2a root2 = (-b-√d)/2a or root2 = (-b-d^(1/2)/2a

OUTPUT "VALUE OF ROOT 1:" +root1 OUTPUT "VALUE OF ROOT 2:" +root2
ELSE IF (d == 0) THEN

root1=root2= -b/2a OUTPUT "VALUE OF ROOT 1:" +root1 OUTPUT "VALUE OF ROOT 2:" +root2
ELSE

OUTPUT "There is no real root"
ENDIF
END

Design (Algorithm)

Start
Take the input of coefficients a, b and c from the user.
Find the value of discriminate (d) = (b * b) - (4 * a * c)
if discriminant > 1

root1 = (-b + √d) / 2a root2 = (-b - √d) / 2a
if discriminant = 1

root1 = -b / 2a root2 = -b / 2a
if discriminant < 1

root1 = -b / 2a + i (√d / 2a) root2 = -b / 2a - i (√d / 2a)
Print the roots
Stop

Turn Learning into Career Growth

1200+Hiring Partners

89%Placement Rate

11,000+Placements

147%Avg Salary Increment

2.5XCareer Growth

₹23 LPAAvg Post-Scaler Salary

1200+Hiring Partners

89%Placement Rate

11,000+Placements

147%Avg Salary Increment

2.5XCareer Growth

₹23 LPAAvg Post-Scaler Salary

Flowchart

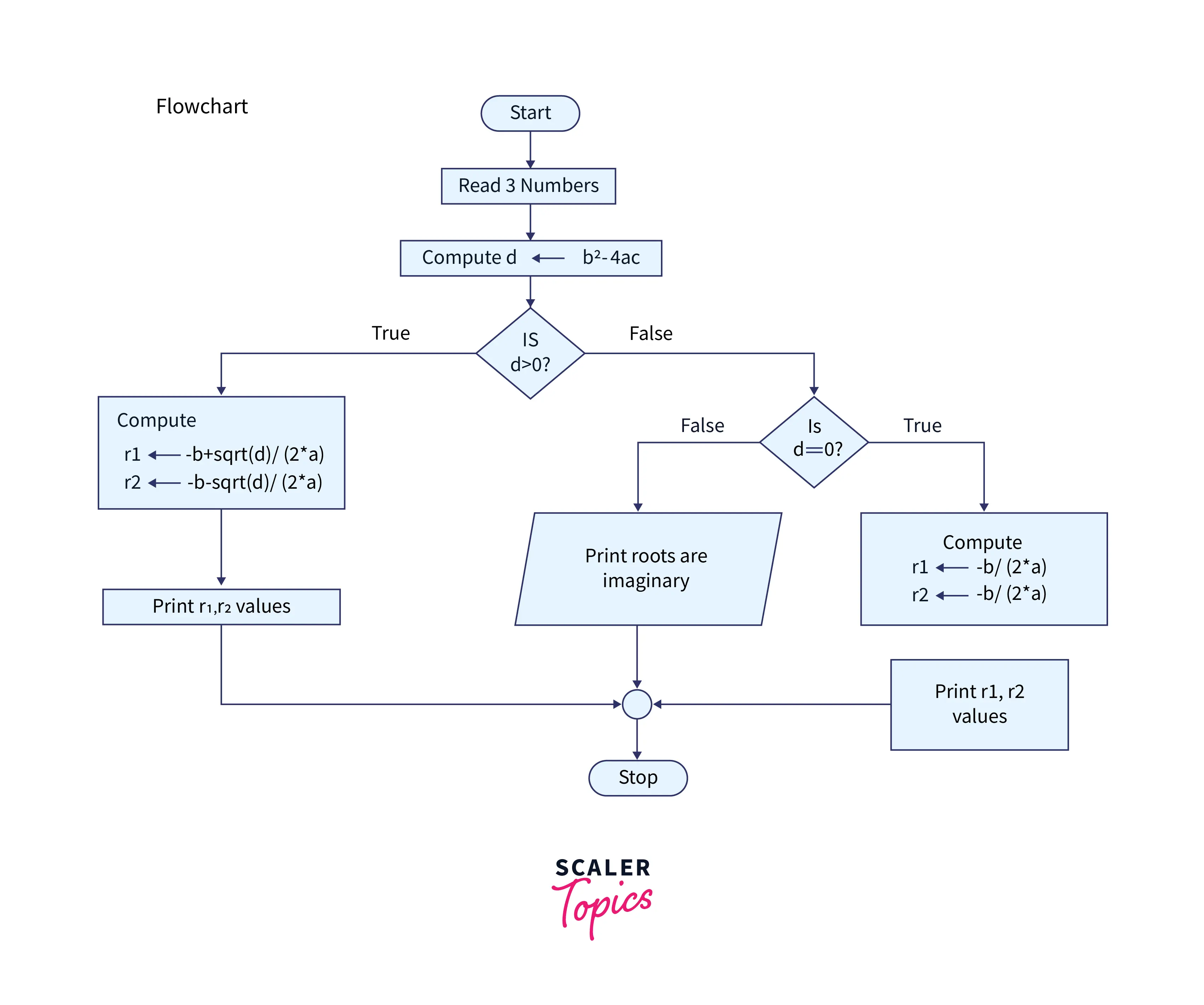
FLOWCHART OF QUADRATIC UNIVERSITY

Scaler Placement Report and Statistics

₹23L

AVG CTC

SCALER PLACEMENT PROOF

Scaler learners achieved 2.5x salary growth with average post-Scaler CTC reaching ₹23L.

11,000+placements

650+companies

Verified data

See full placement report

Implementation Code

Explanation:

In the above c program to find the roots of quadratic equation in c, the variables a, b, and c are the coefficient of the quadratic equation, and the variable d is its discriminant. To find the discriminant (d) we used the sqrt() function, which is defined in the math.h standard library. The sqrt() function is used to find the square root value of a number. The nested if-else statements in the code are used to find the nature of the roots according to the value of the discriminant.

Let's check our code for all three different scenarios.

Assume if the value of a = 1, b = 4, and c = 3, then the output of the above program in c is:

Here, discriminant > 0, and the roots of the quadratic equation are -1 and -3.

Let's see another case when the value of a = 1, b = 2, and c = 1, then the output of the above program is:

The roots of the equation are equal having the value = -1 -1

Here, discriminant = 0, and both the roots of the equation have a value equal to -1.

Another case is when the value of a = 1, b = 1, and c = 4, then the output of the above program is:

Here, discriminant < 0, and hence we can not compute the roots. Time Complexity: O(1)

Auxiliary space Complexity: O(1)

More Examples:

Find the values of a, b, and c in a quadratic equation

Output

Time Complexity: O(1)

Auxiliary space Complexity: O(1)

Conclusion:

Quadratic equations are polynomial equations having a degree of 2. It is represented by the equation, ax² + bx +c = 0, where a, b and c are the coefficients.
The value of a in the equation cannot be zero, and the value of x is used to find the roots of the quadratic equation in c.
The roots of the quadratic equations in c can be defined in three ways: real and distinct, real and equal, and real and imaginary.
The nature of the root is decided by the discriminant and the discriminant has a value of (b²-4ac).
If the value of the discriminant comes to less than zero, then the roots are imaginary and hence can not be computed.
If the value of the discriminant is greater than zero, then the roots are real.
If the value of the discriminant is equal to zero, then both the roots are equal.

Quadratic Equation Program in C

Nature of the Roots

Analysis

Procedure

Transform Your Career

Modern Software and AI Engineering Program

Modern Data Science and ML with specialisation in AI

Advanced AIML with Specialisation in Agentic AI

DevOps, Cloud & AI Platform Engineering

AI Engineering Advanced Certification by IIT-Roorkee

Steps to Find the Square Roots of the Quadratic Equation

Pseudo Code of the Quadratic Equation

Design (Algorithm)

Turn Learning into Career Growth

Flowchart

Scaler Placement Report and Statistics

Implementation Code

Explanation:

More Examples:

Find the values of a, b, and c in a quadratic equation

Conclusion: