Bitwise Operators in C

Overview
Bitwise operators are used to manipulate bits in various different ways. They are equivalent to how we use mathmatical operations like (+, -, /, *) among numbers, similarly we use bitwise operators like (|, &, ^, <<, >>, ~) among bits.
6 Bitwise operators in C
There are 6 bitwise operators in C language. They are
- AND (&)
- OR (|)
- XOR (^)
- COMPLEMENT (~)
- Left Shift (<<)
- Right Shift (>>)
The symbols and names of some of these operators may appear similar to the logical operators, But make no mistake, these are different from them.
Bitwise operators vs Logical operators in C
The bitwise operators like AND, and OR can be sometimes confusing for newbies
If you have previously learned about logical operators, you might have come across Logical AND, and Logical OR. Many people have a tendency to confuse them with the Bitwise AND, and Bitwise OR operators. So, let’s try to understand how are they different from each other.
The logical operators work with Boolean data and return a Boolean value, i.e. True or False.
The bitwise operators in C work with integers, i.e. they take integer inputs, manipulate with their bit and return an integer value. The bitwise AND, and OR use ‘&’ and ‘|’ as their operators, while the logical AND, and OR use ‘&&’ and ‘||’ as their operators.

Types of Bitwise operators in C
Now that you know the difference between the logical and bitwise operators, and what are the bitwise operators, let’s look at each one of them in detail.
AND (&)
The bitwise AND operator is denoted using a single ampersand symbol, i.e. &. This is a binary operator, it needs two operands -- two integers -- to work on.
It takes the binary values of both the left and right operands and performs the logical AND operation over them on the bit level, i.e. if both the operands have 1 on the specified position then the result will also have 1 in the corresponding position or else there will be 0.
| Num1 | Num2 | Result=Num1 & Num2 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Truth table for Bitwise AND operator in C
Code
Output
Working:
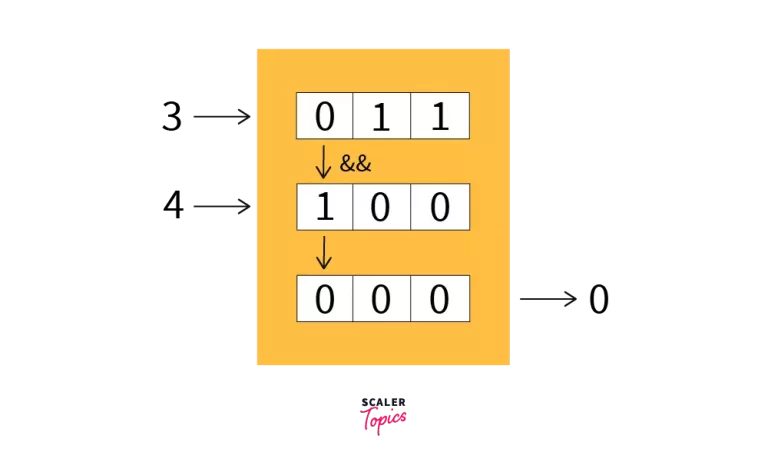
- The above code snippet performs the bitwise AND operation on 3 and 4. Let’s see their working in detail.
- The binary value for 3 is 11 and 4 is 100.
- First, we have to convert the shortest binary value to the length of the longest one, by adding zeros to the left side - the most significant bit.
- Here the number with the shortest length is 3, with lengths 2 and the largest one is 4 with length 3. Convert them to the same length by adding 0s as the most significant bit in 3.
- So, now we have 011 as binary representation for 3 and 100 for 4.
- Now move from left to right, and perform logical AND operations on the bits and store the result in the corresponding position.
- The first bit of 3 is 0 and the first bit of 4 is 1, the logical AND will consider 0 as False and 1 as True, so the result will be false and 0 will be the first bit of the result.
- The same process repeats itself throughout the length of the binary values. The second bit of 3 and 4 are 0 and 0 respectively, so again 0 will be stored as the second bit of the result.
- The third and last bit of both 3 and 4 are 0 and 0, so again 0 will be the third and final bit of our result.
- So the final binary value of our result will be 000, which when converted to integer decimal results to 0.
OR
The bitwise OR operator is much similar to the bitwise AND, the only difference is that the bitwise OR operator performs logical OR instead of logical AND on the bit level, i.e. if at least any one of the operands have 1, then the result will also have 1 in the corresponding position, and 0 if they both have 0 in the corresponding position.This is denoted using the vertical bar or pipe symbol, i.e. |.
| Num1 | Num2 | Result=Num1 | Num2 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Truth table for Bitwise OR operator in C
Code
Output
Working
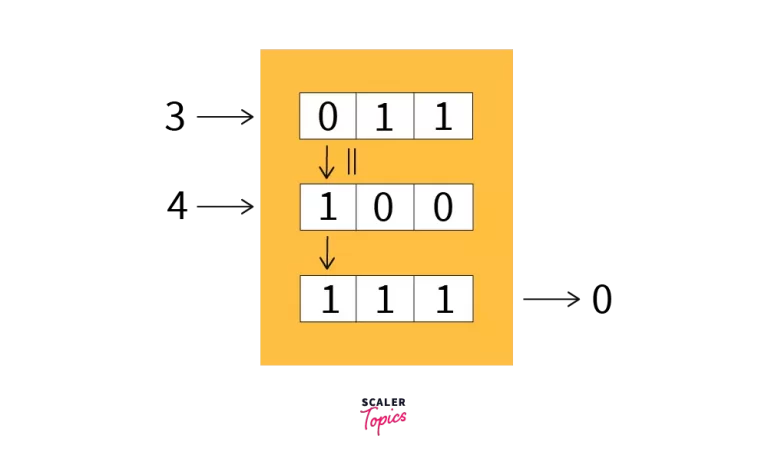
- The above code snippet performs the bitwise OR operation on 3 and 4. Let’s see their working in detail.
- The binary value for 3 is 11 and 4 is 100.
- First, we have to convert the shortest binary value to the length of the longest one, by adding zeros to the left side - the most significant bit.
- So, now we have 011 for 3 and 100 for 4.
- Now move from left to right, and perform logical OR operations on the bits and store the result in the corresponding position
- The first bit of both 3 and 4 are 0 and 1, respectively, so the first bit of the result is 1.
- The second bit of both 3 and 4 are 1 and 0, respectively, so the second bit of the result is also 1.
- The third bit of both 3 and 4 are 1 and 0, respectively, so the third bit of the result is also 1.
- So the binary value of the result is 111, which when you convert from binary to decimal returns 7.
XOR
This is similar to the other two, but the only difference is that they perform logical XOR on the bit level, i.e., if exactly one of the operands has 1 and the other has 0 then the result will have 1 in the corresponding position, and 0 if they have the same bits such as both 0s or both 1s.
| Num1 | Num2 | Result=Num1^Num2 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Truth table for Bitwise XOR operator in C
Let’s continue with the same example that we used for the previous two operators.
Code
Output:
Working:
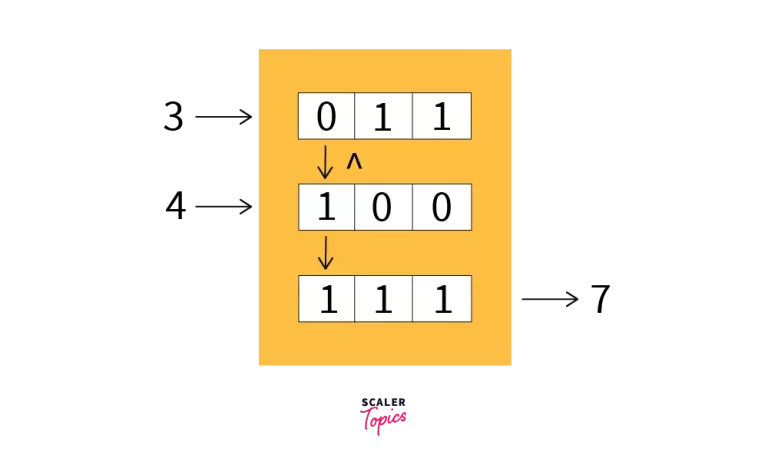
- The above code snippet performs the bitwise XOR operation on 3 and 4. Let’s see their working in detail.
- The binary value for 3 is 11 and 4 is 100.
- First, we have to convert the shortest binary value to the length of the longest one, by adding zeros to the left side — the most significant bit.
- So, now we have 011 as binary representation for 3 and 100 for 4.
- Now move from left to right, and perform logical XOR operations on the bits and store the result in the corresponding position.
- The first bit of both 3 and 4 are 0 and 1, respectively, so the first bit of the result is 1.
- The second bit of both 3 and 4 are 1 and 0, respectively, so the second bit of the result is also 1.
- The third bit of both 3 and 4 are 1 and 0, respectively, so the third bit of the result is also 1.
- So the binary value of the result is 111, which when you convert from binary to decimal returns us with 7.
So far, we have seen three bit wise operators in C, let’s take a look at their collective truth table before we move onto further operators.
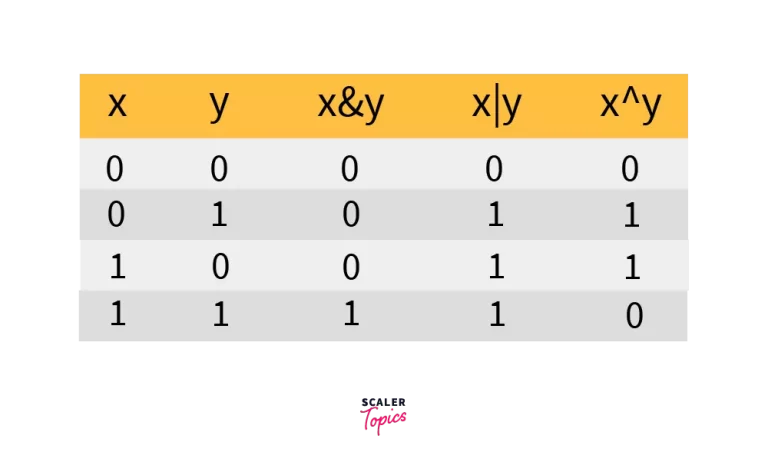
A collective truth table for Bitwise AND, OR and XOR operators in C.
COMPLEMENT
We have seen three bitwise so far, if you have noticed, all of them were [binary operators](https://www.scaler.com/topics/binary-operator-in-c/, i.e. they all require two operands to perform their functions. But this one is different, this is the only bitwise operator that requires only one operand. All other bitwise operators require 2 operators.
The bitwise complement operator takes a single value and returns the one’s complement of the value. The one’s complement of a number is obtained by changing all the 0’s in its binary value to 1’s and by changing the 1’s to 0’s.
It is denoted using the tilde symbol, i.e. ‘~’.
| Num1 | Result = ~Num1 |
|---|---|
| 0 | 1 |
| 1 | 0 |
Truth table for Bitwise Complement operator in C
Code
Output
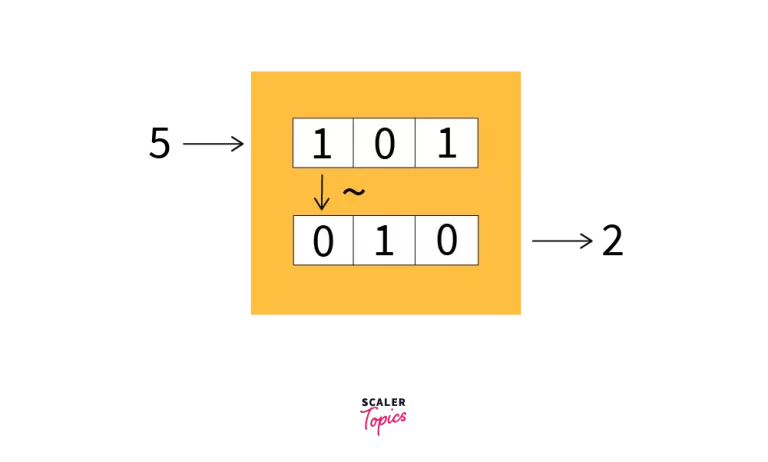
Working:
- The above code snippet performs the bitwise COMPLEMENT operation on 5.
- Flips all the bits and 101 gives us 010 which is 2 in decimal form.
Note:
- here, logically ~5 = 2 but, the compiler returns the 2’s complement of the input value.
- Negative numbers are stored as 2’s complement
- Binary equivalent of 5 is 0000 0101
- One ‘s complement of 5 is 1111 1010
- 6 is represented in binary as 0000 0110
- One ‘s complement of 6 is 1111 1001
- Add one to its one's complement to get two's complement of 6 = 1111 1010
- This equates to ~5.
- As a result, 6 is the bitwise complement of 5.
So far, we have learned about four bitwise operators in C. All of them were quite similar to the logical operators, i.e. they performed the same operation on the bit level, which the logical operators performed on boolean variables. But the next two operators we are going to see are quite different.
Shift Left
The shift left operator shifts the bit pattern of an integer value by a specified number of bits to the left.
The Shift Left operator takes two operands, a value on which the shift operation is to be performed, say ‘x’, and another value that specifies the number of bit positions that have to be shifted on the fore mentioned value, say ‘n’.
The value of ‘x’ can be negative, but not that of ‘n’, if the value of ‘n’ is negative then the compiler will throw an error, saying ‘negative shift count’
When the value of 'x' is negative, the Left Shift operation is performed on the two’s complement of the number. So there is a possibility that the sign of the number may or may not be the same as the left shift operation. The Shift Left operator is denoted using two consecutive greater than operators, i.e. <<.
This is equivalent to multiplying the number by 2 power n, again assuming that n is the operand to the operator’s right.
Why is it so?
This is a fairly simple question that many people find themselves asking, whenever you shift a number to the left you are actually multiplying it with the base value. Consider 3 in decimal value, when you shift it to the left and add 0s to its right most end you are actually multiplying it with 10, which is its base value.
E.g. when you shift 3 left by 1 position, you get 30 which is 3*10. The same is true with any base values. Since the shift left operator works with binary values, the result is equivalent to multiplying with the powers of 2.
Syntax:
Code:
Output:

Working:
- The above code snippet performs the left shift operation on the decimal value 5.
- It shifts the bit patterns of 5 by 2
- The binary value for 5 is 101.
- When you shift it to the left by 2 positions and add 2 0s to the right most end of the binary sequence, i.e. the least significant bit, the result that you get is 10100.
- The result when converted from binary to decimal will be 20
Shift Right
The shift right operator is almost similar to the shift left operator, the only difference is that it shifts the bit to the bits to right instead of left. This pops the last n bits from the given value and converts the remaining bits from binary to an integer.
The same rule that we saw in the Shift Left operator also applies for the Shift Right operator. The value of ‘x’ can be negative, but not that of ‘n’, if the value of ‘n’ is negative then the compiler will throw an error, saying ‘negative shift count’
Just as in the Left Shift operator, When performing Right shift operation on a negative number, the Right Shift operation is performed on the two’s complement of the number.
So when you perform Right Shift operation on a negative number, the result will be a positive number, cause when you perform Right Shift operation you replace the sign bit with 0, after shifting the previously present 1 to the next bit position.
It is denoted using two consecutive less than symbols, i.e. >>.
Syntax:
This is equivalent to the floor division of the given number using 2 power n.
As like in Left Shift operation, whenever you shift a number to right, you are actually dividing it with the base value. Consider 345 in decimal value, when you shift it to the right and pop the last character, in its right most end you are actually dividing it with 10, which is its base value.
E.g. when you shift 345 left by 1 position, you get 34 which is 345/10. The same is true with any base values. Since the shift Right operator works with binary values, the result is equivalent to dividing with the powers of 2.
Code:
Output:
Working:
- The above code snippet performs the Shift Right operation on the decimal value 20.
- It shifts the bit patterns of 20 by 2
- The binary value for 20 is 10100.
- When you shift it to the right by 2 positions, i.e. Pop the last 2 bits, the result that you get is 101.
- The result when converted from binary to integer produces 5
Conclusion
In this article, you learned about what is bitwise operators, how are they different from logical operators, and what are the bitwise operators in C programming language.
Bitwise operation can help you save a lot of time when you use them properly, some of the most commonly used bit manipulation techniques applications are
- Use OR '|' and space bar coverts English characters to lowercase
- Use AND '&' and underline coverts English to uppercase.
- Use XOR '^' and space bar for English characters' case exchange.
- Swapping two numbers.
- Check whether the given number is an exponent of 2
Hope you learned something new from this article.
Thank You 👋
