Evaluation of Arithmetic Expression

Overview
Arithmetic expressions can be written in 3 different notations - infix, prefix, and postfix. In the Prefix notation, the operator is written before the operand in an expression. On the other hand, in the Postfix notation, the operator is written after the operand. The expressions are evaluated using stack.
Introduction
An expression that only contains arithmetic operands and operators is called an arithmetic expression. The results of these expressions are always in numeric values. Arithmetic expressions are usually represented in something known as the Infix Notation. In this notation, the operator is between two operands (Example: X + Y where X and Y are arithmetic operands). We can even use parentheses in arithmetic expressions.
Any arithmetic expression is written in the infix notation is evaluated by following operator precedence rules. However, if we want to evaluate an expression without considering operator precedence, we can use Polish (or Prefix) notations or Reverse Polish (or Postfix) notations.
Types of Expression Evaluation in C
There are four types of expression evaluation in the C programming language:
- Evaluation of Arithmetic Expressions - Arithmetic expressions return numeric values. For example: .
- Evaluation of Relational Expressions - Relational expressions is used to compare two operands. For example: .
- Evaluation of Logical Expressions - Logical expressions return either true or false values. For example: .
- Evaluation of Conditional Expressions - If a conditional expression is true, it returns a particular statement/expression. But if it is false, it returns another statement/expression. For example: (10 > 3)? "expression is true" : "expression is false". In this example, since 10 > 3 is true, the statement "* expression is true" will be returned. Had it not been true, the statement "expression is false" would have been printed.
In this article, we will learn about arithmetic expressions' evaluation.
The Order of Evaluation For Arithmetic Expressions
To evaluate arithmetic expressions, the compiler has a pre-defined order in which it evaluates any expression. The order of evaluation followed by the compiler is:
-
The expressions with parentheses are evaluated first. If two or more parentheses exist in an expression, the parentheses are evaluated from left to right. In the case of nested parentheses, the innermost parentheses are evaluated first, while the outermost one is evaluated last.
-
If there are no parentheses, the order of evaluation of an expression is based on the operator precedence and associativity:
Precedence Operator Associativity 1 Unary plus, Unary minus Left to Right 1 Built-in functions Left to Right 2 Multiplication and Division Left to Right 3 Addition and Subtraction Left to Right
Suppose parentheses do not specify the sequence of execution of an expression, and two or more operators have the same precedence. In that case, the order of evaluation is from left to right.
Let us understand this topic with an example of the infix notation:
Answer:
Steps to evaluate the above expression:
- In the above expression, unary minus has the highest precedence. So, it will be solved first. The expression will simplify to: 8 * sqrt(25) + 3.
- Since sqrt(25) is a built-in function, it will be evaluated next. The expression will now become: .
- Next, multiplication will be performed. The expression will become 40 + 3.
- Finally, the addition will be performed. So, the answer will be 43.
Let us take another example:
Answer:
Steps to evaluate the above expression:
- Parentheses have the highest precedence. So, the expressions inside the parentheses will be evaluated first. After solving, the whole expression simplifies to: .
- Now, multiplication and division have the same precedence. Since multiplication and division have associativity from left to right, multiplication will be performed first. The expression now becomes: .
- Next, the division has higher precedence. So, the expression will become .
- Finally, we will subtract 3 from 14 to get 11 as the output.
Polish (or Prefix) Notation
In the Polish or Prefix notation, the operator is written before the operand in an expression. This notation does not need parenthesis because the expression's evaluation is done in a stack. So, we do not need to specify the execution order to evaluate arithmetic expressions. The compiler can process the prefix notation faster than the infix notation because it does not need to process any parentheses or follow precedence rules. An expression in the Polish notation looks like this:
The above expression is equivalent to X * Y in the infix notation where X and Y are two arithmetic operands and * is the operator.
The steps for evaluating a prefix expression differ from the steps we commonly perform to evaluate the infix expression. We can calculate the value of the arithmetic operations by using a stack. Here are the steps to evaluate the value of a prefix expression:
- Place a variable var at the last element of the expression.
- If the variable var points to:
- An operand, push that element to the stack.
- An operator X, pop two elements (operands) from the stack and operate on the popped operands using the operator X. Once the operation is performed, push the calculated value back to the stack.
- Decrement the variable's value by 1.
- Repeat steps 2 and 3 until all the elements have been traversed.
- Return the only value present in the stack at the end.
Let us now take an example to understand how arithmetic expressions are evaluated using the prefix notation.
Answer:
Using the steps discussed above, we will calculate the value of this expression.
Step 1: Place a pointer at the last element, i.e., 2 in this example.
Step 2: Since 2 is an operand, we will push it to the stack. The stack will look like this:
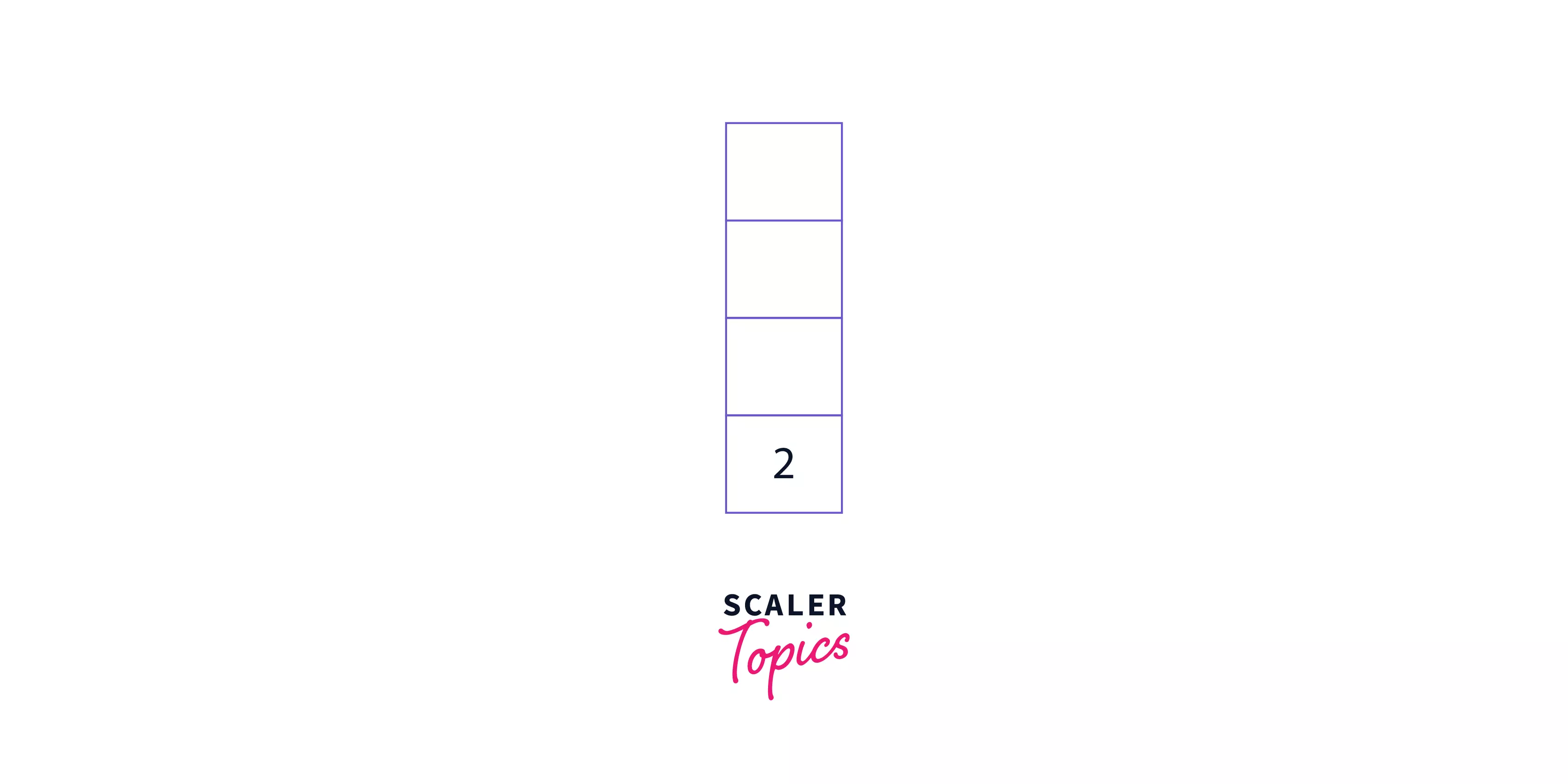
Step 3: We now decrease the pointer's value by 1 so that it points to the last number, which is 8. Once again, 8 is an operand, so we push it to the stack. Similarly, these steps will be repeated until the stack looks like this:
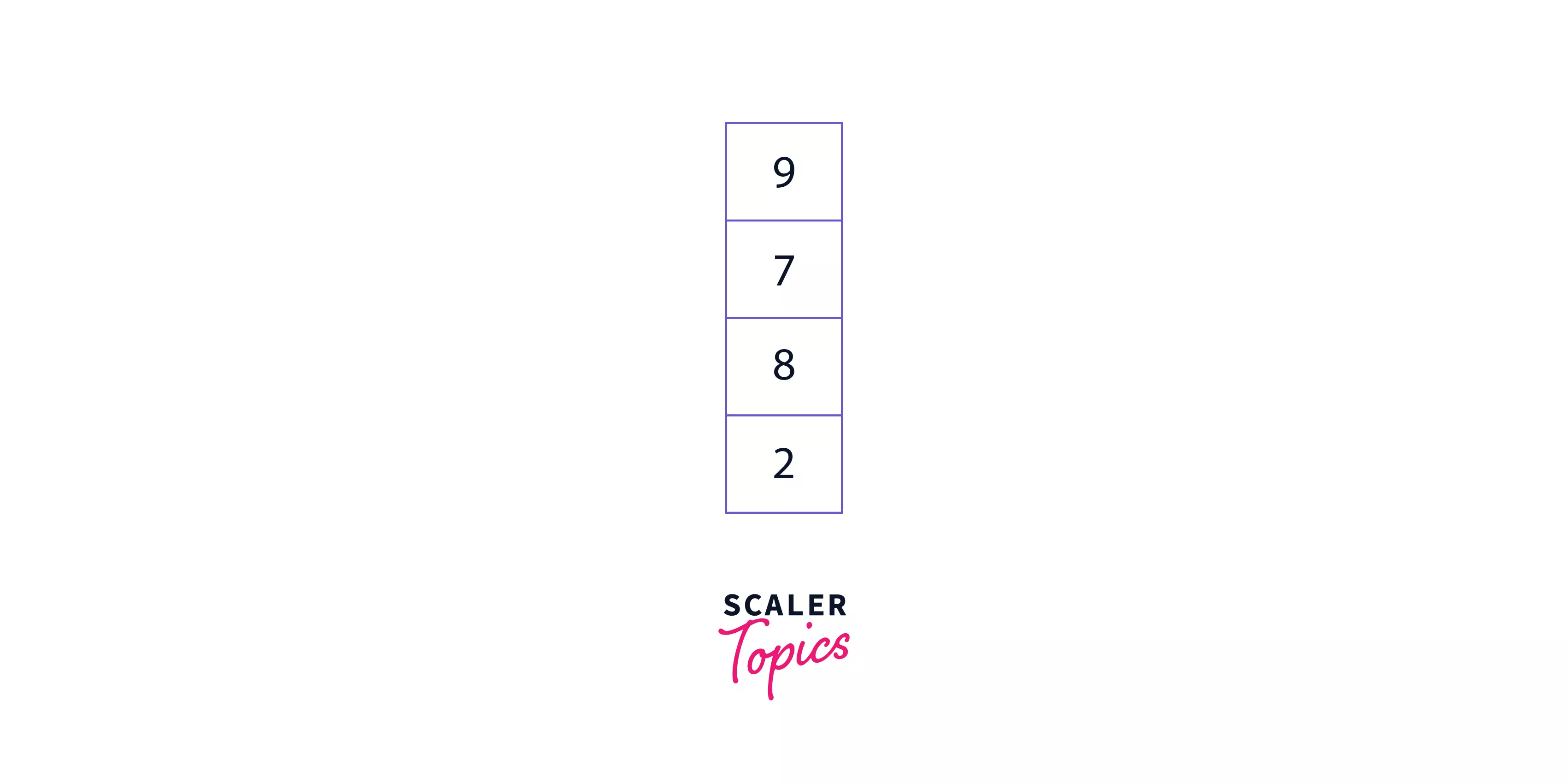
Step 4: Reducing the value of the pointer by 1 yet again, we will encounter an operator i.e., +. So, we will remove the top two elements from the stack (9 and 7) and add them. 16 (9 + 7) will be added to the stack. The stack now looks like this:
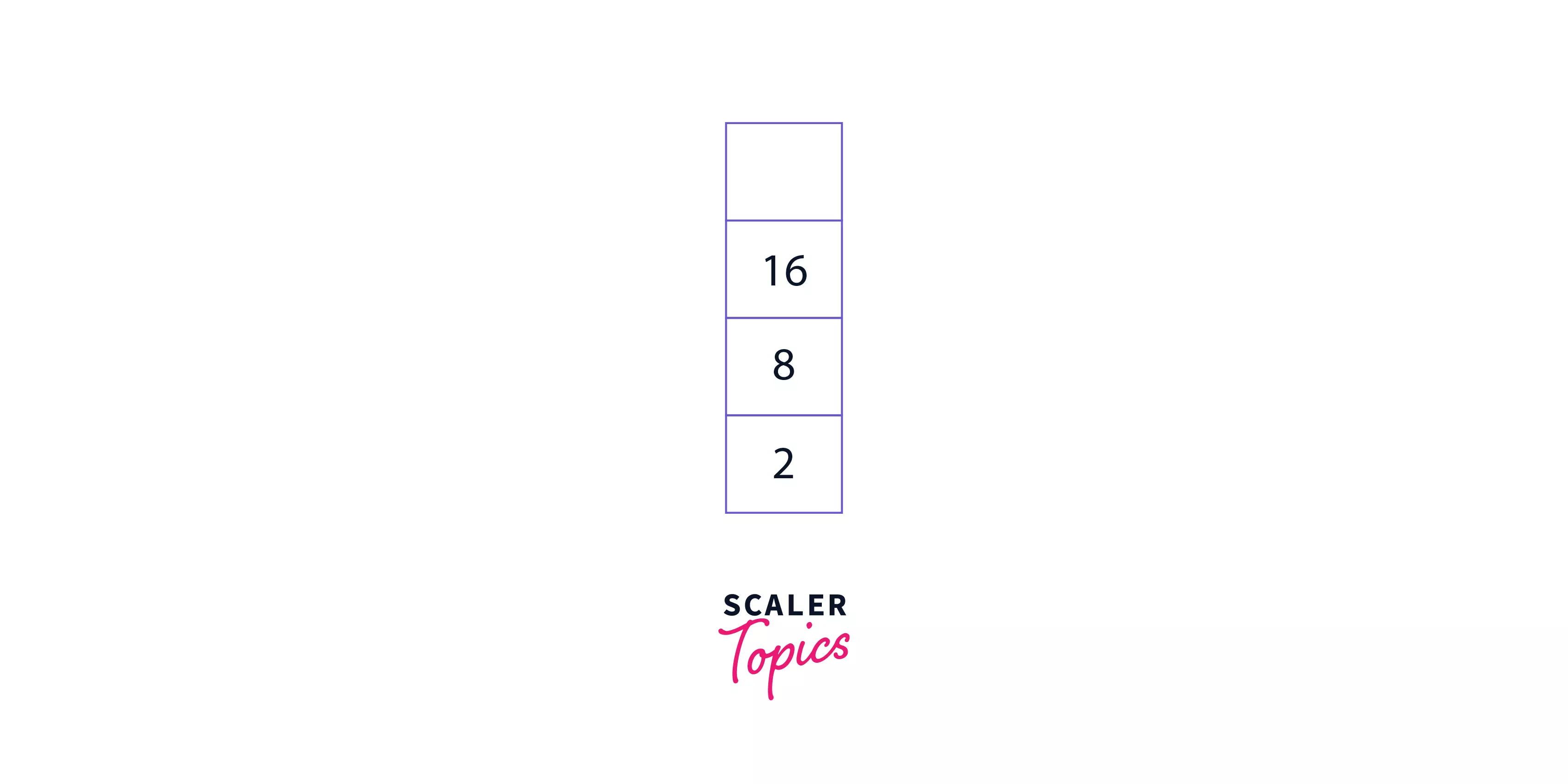
Step 5: Once again, decrease the value of the pointer and repeat the steps. Finally, after completing all calculations, we will get:
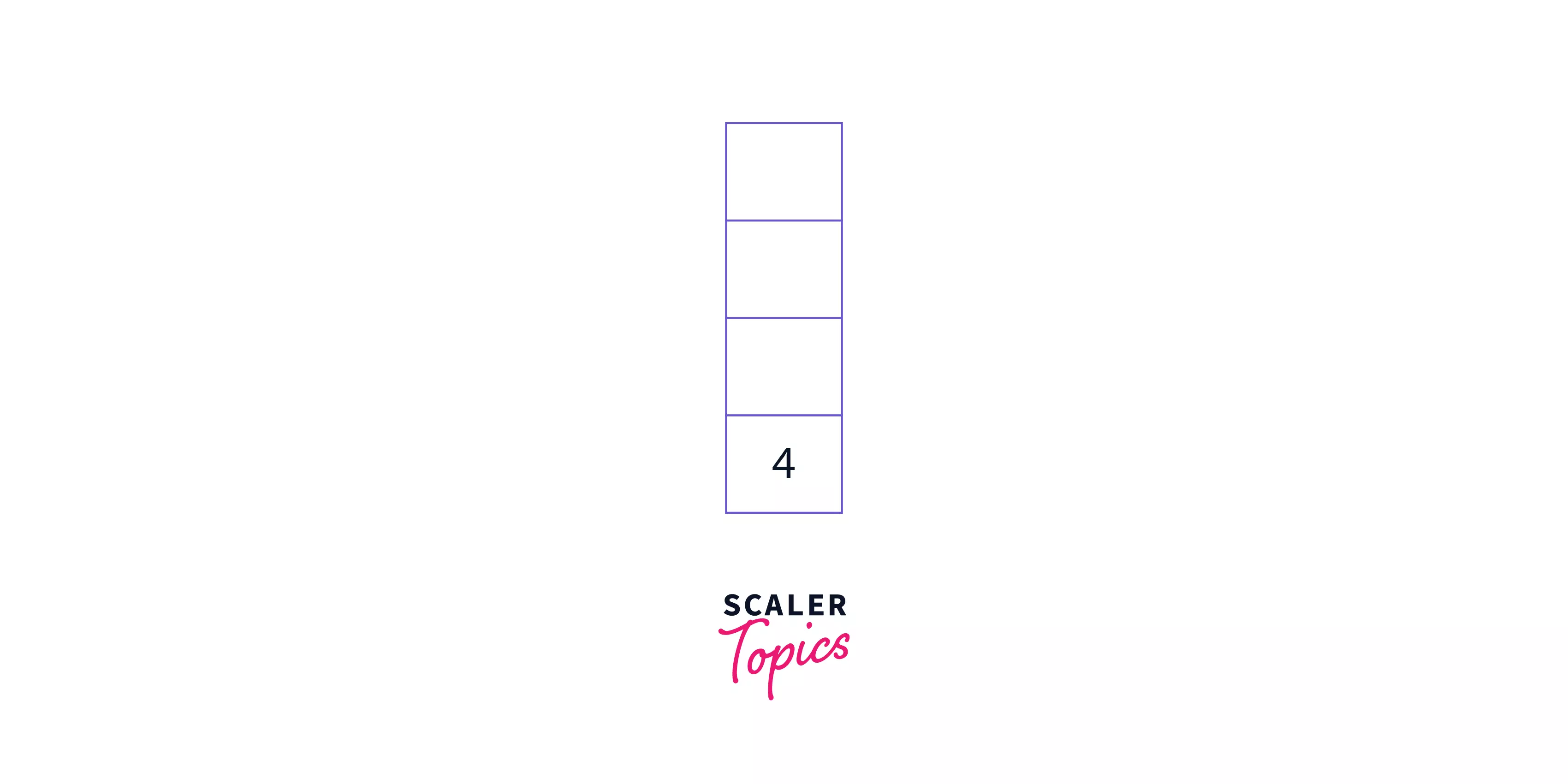
Step 6: Return the value present in the stack to get the final answer. Hence, the answer is 4.
Reverse Polish (or Postfix) Notation
In the Reverse Polish or Postfix notation, the operator is written after the operand in the expression. There is no need for parenthesis in this notation because the expression's order of execution is already defined in the stack. An expression in postfix notation looks like this:
The above expression is equivalent to X + Y, where X and Y are two arithmetic operands, and + is the operator.
The evaluation of arithmetic expressions in postfix notation is similar to the evaluation of arithmetic expressions in prefix notation. We can also calculate the value of the arithmetic operations by using a stack. Here are the steps to evaluate the value of a postfix expression:
- Place a pointer at the first element of the string.
- If the pointer points to:
- An operator X, pop the top two elements (operands) from the stack and operate using the operator X.
- An operand, push that element to the stack.
- Increase the value of the pointer by 1.
- Go to step 2 if elements are left to be scanned in the expression.
- Return the result stored in the stack.
Let us take an example to understand how to evaluate arithmetic expressions:
Answer:
Using the steps described above, let us calculate the value of this expression.
Step 1: Place a pointer at the first element, 5.
Step 2: Because 5 is an operand, push it to the stack. The stack now contains - [5].
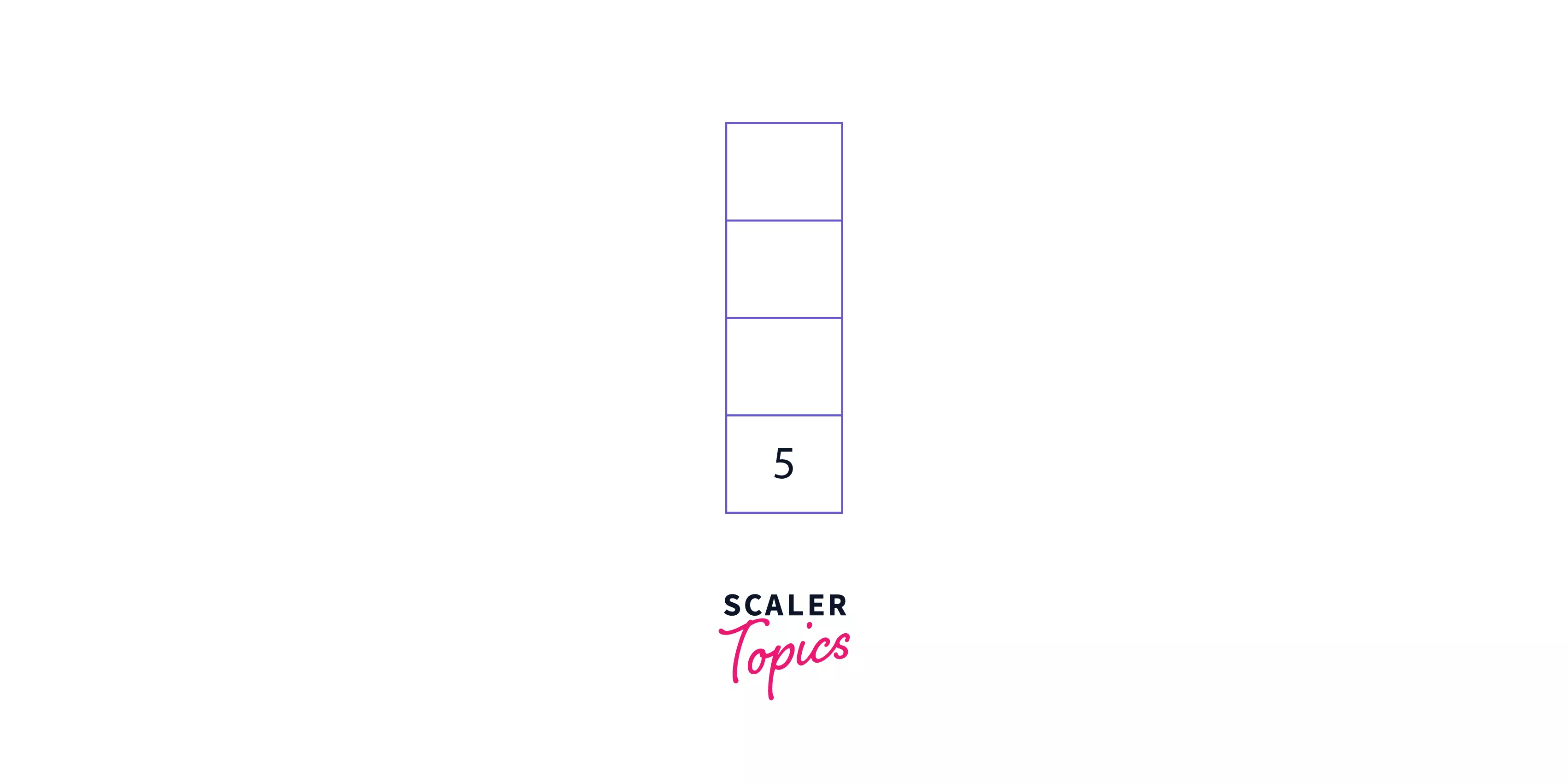
Step 3: Now, increase the value of the pointer by 1. The pointer will now point at the second element, 3. Again, because 3 is an operand, push it to the stack. The stack now contains - [5 3] (bottom to top).
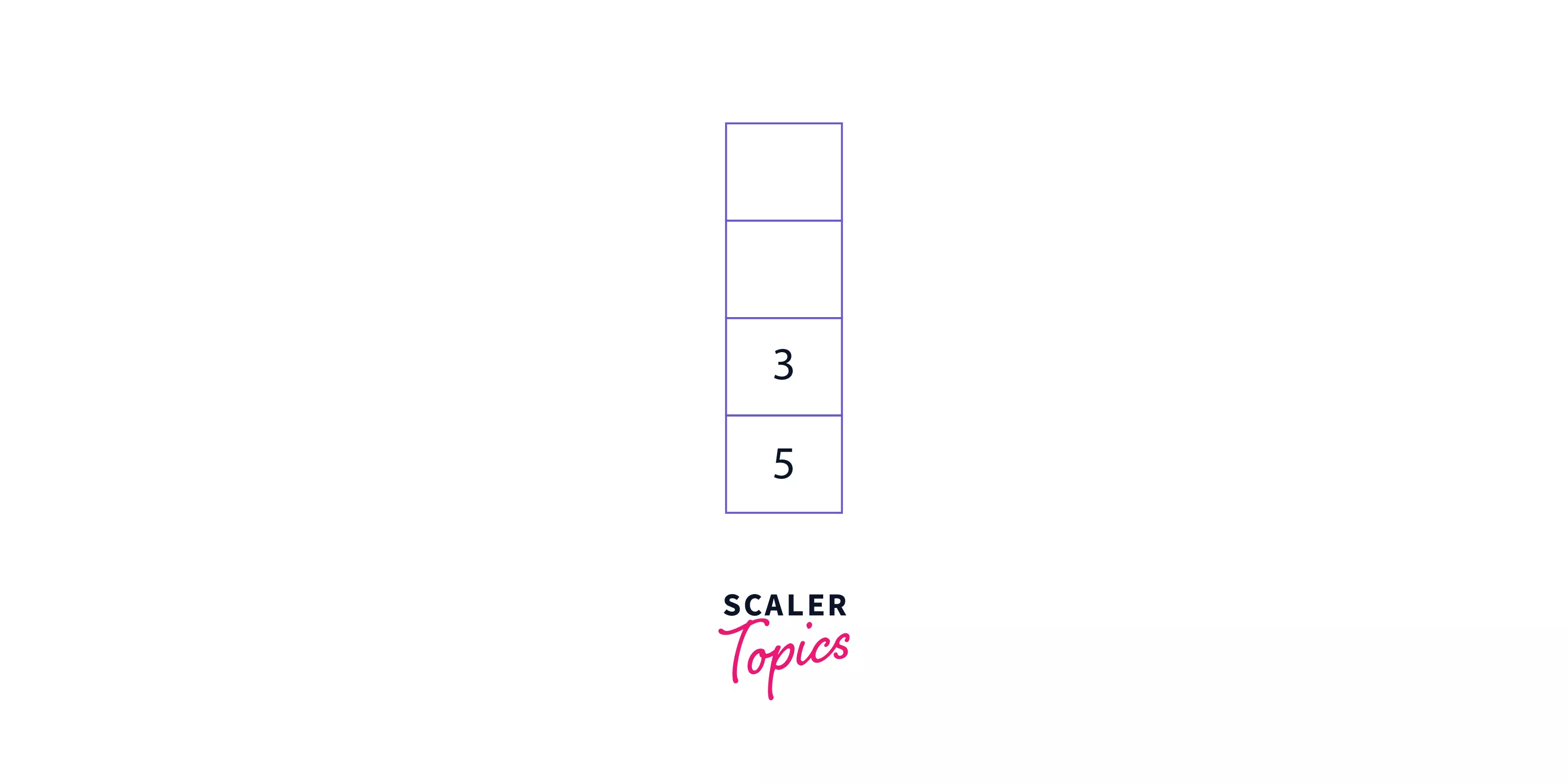
Step 4: Repeat the process in Step 3. The stack now contains - [5 3 7]
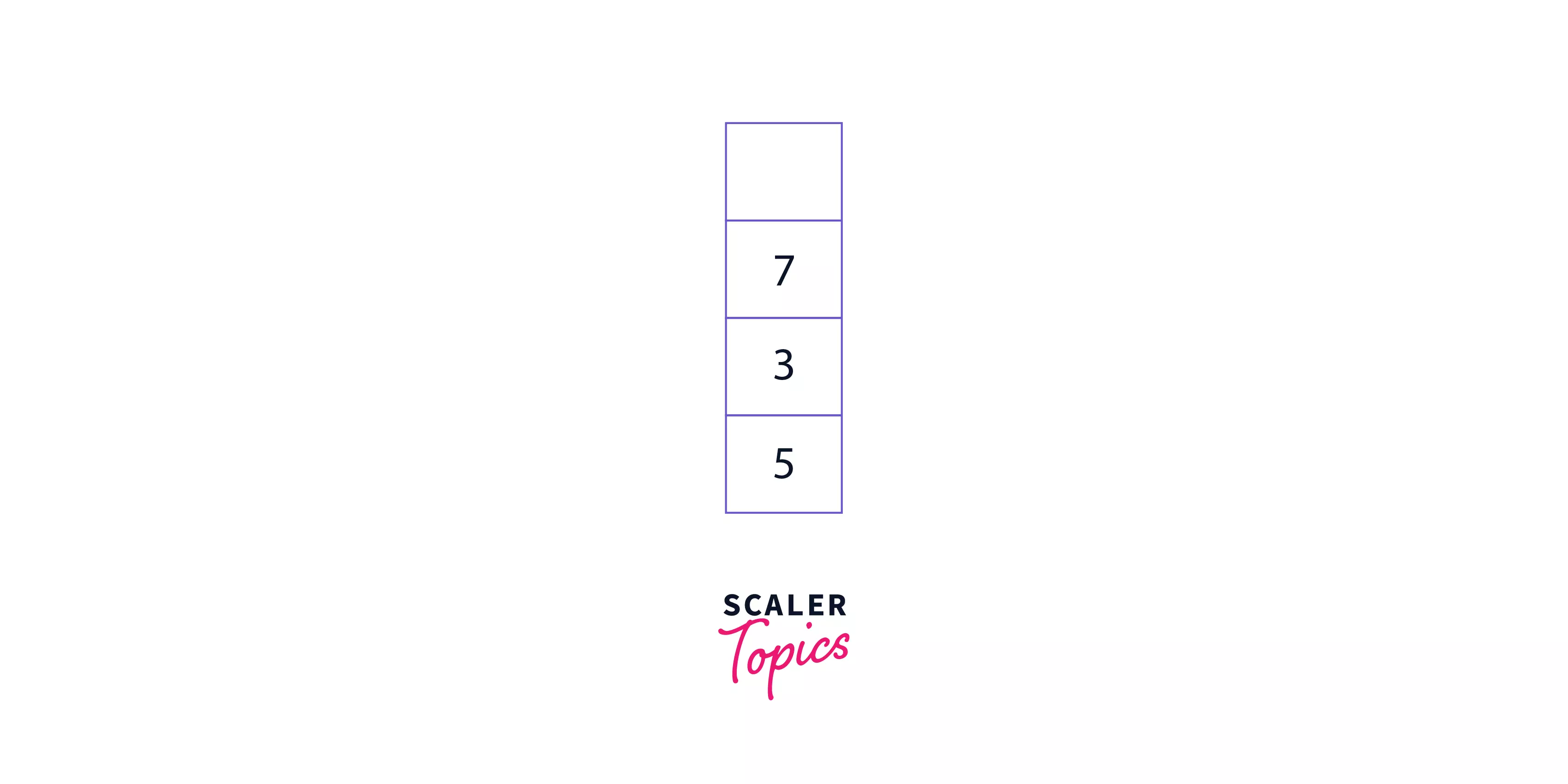
Step 5: Increase the value of the pointer once again. The pointer now points at the operator *. So, take out the top two operands from the stack (7, 3) and perform a multiplication operation on them. Then, push the calculated value back into the stack. The stack now contains - [5 21].
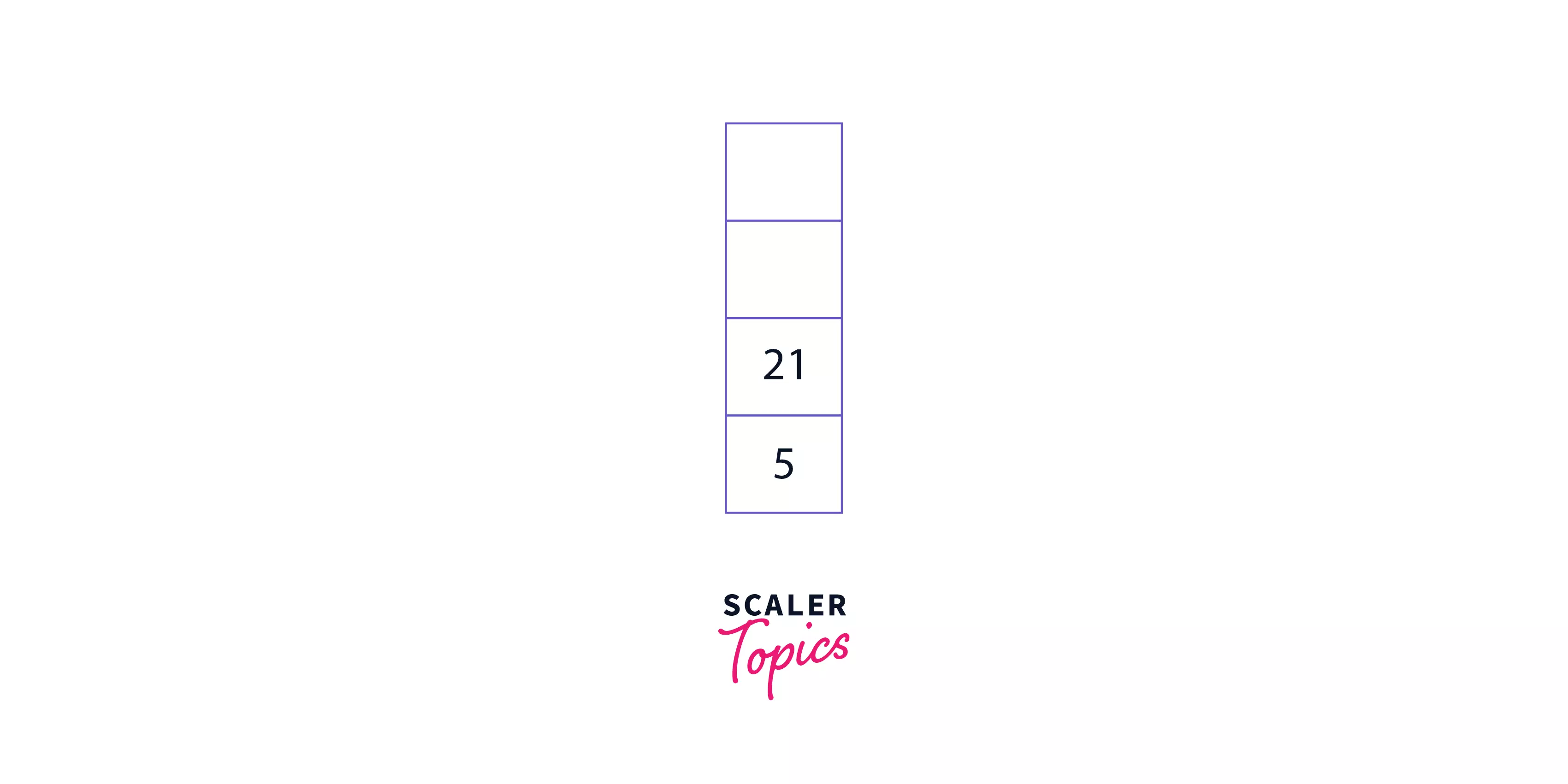
Step 6: Repeat the above steps so that the stack contains - [4 26].
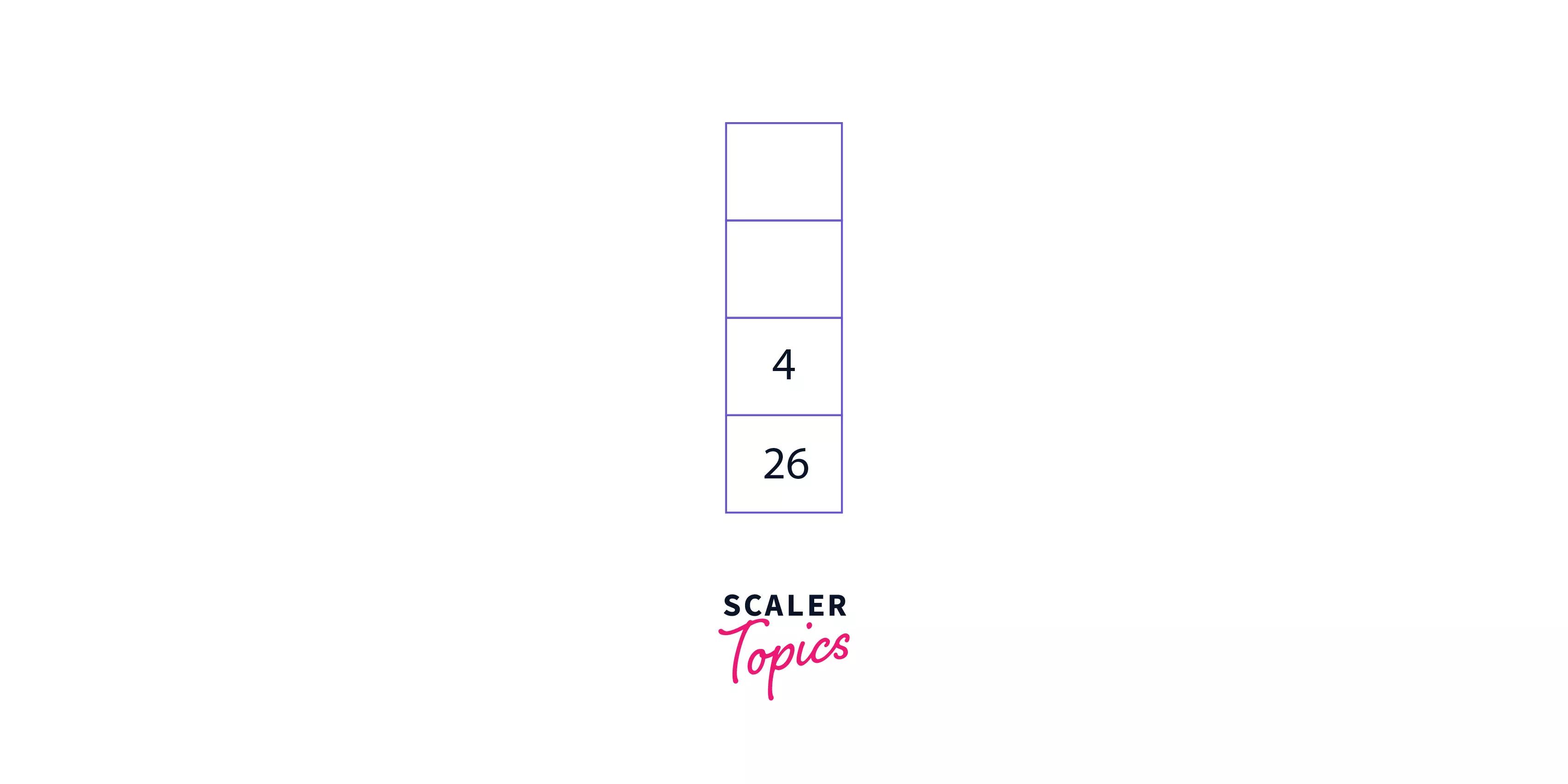
Step 7: Increase the value of the pointer to perform the final operation. Now, there are no more elements left in the expression, and [22] is the only element left in the stack. Hence, the answer is 22.
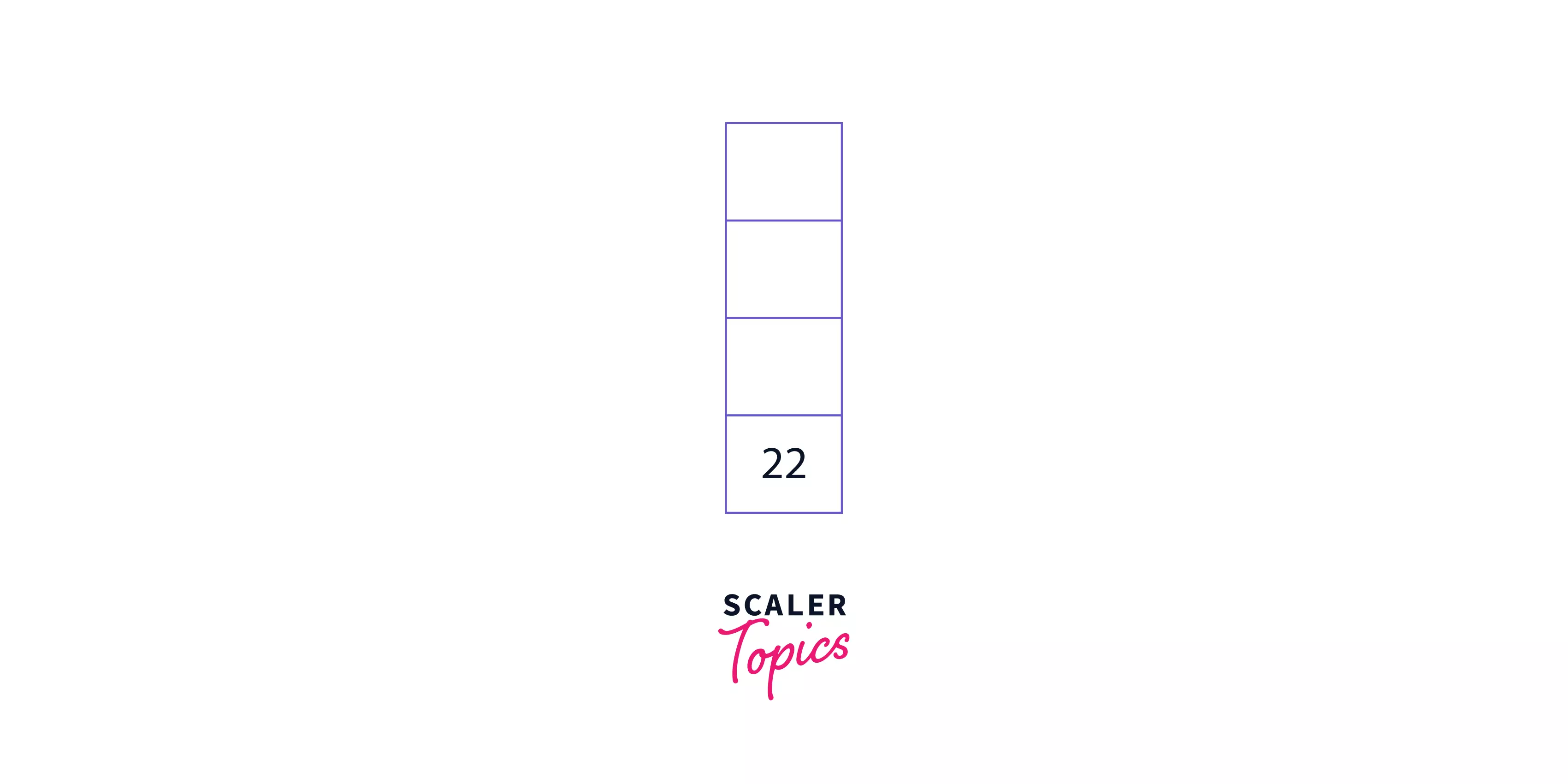
Table to Convert Infix Notations to Prefix and Postfix Notations
Although infix notation is the most common notation used by us, computers prefer prefix or postfix notations for the evaluation of arithmetic expressions because they are quicker to execute than the infix notations.
Since prefix and postfix notations are necessary for programming, we should know the typical expressions in the infix notation and their conversion to prefix and postfix notations. A table containing the standard expressions to convert infix notation to prefix or postfix notation is given below.
| Serial Number | Infix Notation | Prefix Notation | Postfix Notation |
|---|---|---|---|
| 1 | m + n | + m n | m n + |
| 2 | m ∗ (n + o) | ∗ m + n o | m n o + ∗ |
| 3 | (m + n) ∗ o | ∗ + m n o | m n + o ∗ |
| 4 | (m + n) ∗ (o + p) | ∗ + m n + o p | m n + o p + ∗ |
| 5 | m / n + o / p | + / m n / o p | m n / o p / + |
| 6 | ((m + n) ∗ o) - p | - ∗ + m n o p | m n + o ∗ p - |
Precedence For 5 Binary Operators
The five binary operators: ^, \*. /, +, and - have three levels of precedence. The associativity of these operators is from left to right.
| Precedence | Operator Name | Operator | Associativity |
|---|---|---|---|
| 1 | Exponentiation | ^ | Left to Right |
| 2 | Division and Multiplication | / \* | Left to Right |
| 3 | Addition and Subtraction | + - | Left to Right |
The above table shows the default behavior of binary operators. The order of evaluation of arithmetic operators can be altered using parentheses. Calculate the value of these arithmetic operations by using a stack
Summary
- Arithmetic expressions can be written in 3 different notations - infix, prefix, and postfix.
- In the Prefix notation, the operator is written before the operand in an expression. On the other hand, in the Postfix notation, the operator is written after the operand.
- Prefix and Postfix notations are faster than infix notations.
- We can convert infix notations to prefix or postfix notations and vice-versa.
