How to Convert Octal to Binary?
In the world of computers and digital information, numbers take on a unique form, far removed from the familiar decimal system we use in everyday life. These numbers, known as binary and octal numbers, form the foundation of digital communication and computation.
Binary numbers, the language of computers, consist solely of two digits: 0 and 1. These digits represent the on/off states of transistors within electronic circuits, forming the very essence of digital data. While binary numbers may appear cryptic to the human eye, they provide a concise and efficient representation of information that computers can seamlessly process.
Octal numbers, on the other hand, serve as a bridge between the binary world of computers and the human realm. This base-8 system utilizes eight digits: 0, 1, 2, 3, 4, 5, 6, and 7. Each octal digit corresponds to three binary digits, making it a more human-readable representation of binary data.
How to Convert Octal To Binary?
Converting Octal to Binary involves a systematic process that leverages the positional values of each digit in the octal number. Here's a step-by-step guide along with examples:
Step-by-Step Process
-
Write Down the Octal Number: Start with the given octal number.
-
Convert Each Octal Digit to Binary: Convert each digit of the octal number to its binary equivalent. Use a binary table or perform the conversions manually.
-
Combine Binary Digits: Combine the binary equivalents of each octal digit to obtain the final binary representation.
Example 1: Convert Octal 3244 to Binary
Follow the below 2 steps –
- Take each octal digit and convert it to its equivalent binary 3-bit group .
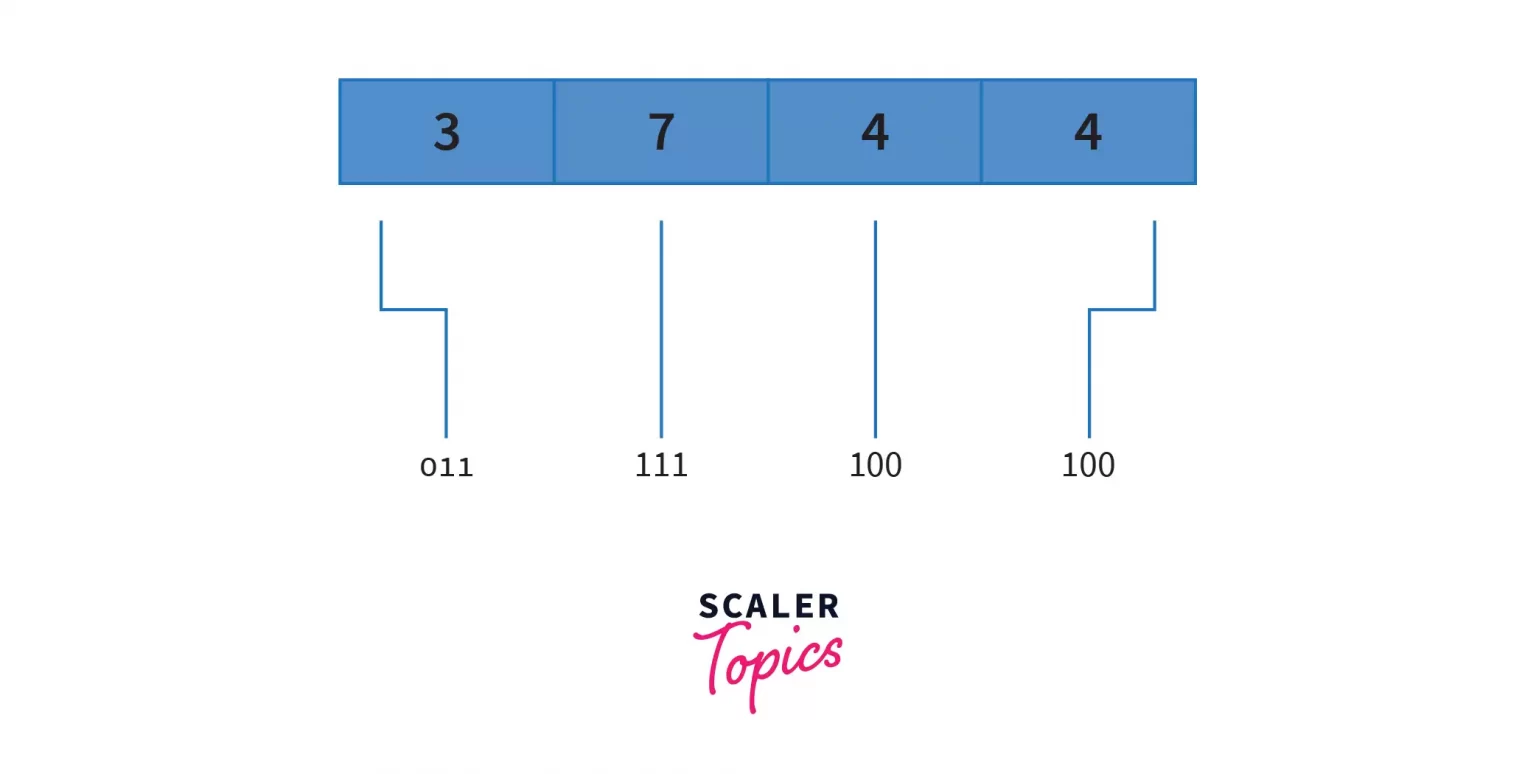2. Append all the binary bit groups together,
we get 011 111 100 100 or 011111100100
Example 2: Convert Octal 246 to Binary
-
Given Octal Number: 246
-
Convert Each Octal Digit to Binary:
- 2 in Octal is 010 in Binary
- 4 in Octal is 100 in Binary
- 6 in Octal is 110 in Binary
-
Combine Binary Digits: Combine the binary equivalents: 010100110
Result: Octal 246 is equivalent to Binary 010100110.
Important Notes:
- The conversion process involves converting each octal digit independently.
- Binary equivalents of each octal digit can be found using a binary conversion table or manually determining the values.
- The final binary result is obtained by combining the binary equivalents of all octal digits.
Convert Octal to Binary Using Table
The following table shows you the representation of numbers ranging from 0 to 7 in both binary and octal number systems
Example: Convert Octal 2021 to Binary
Octal to Binary Conversion Table:
| Octal Digit | Binary Equivalent |
|---|---|
| 2 | 010 |
| 0 | 000 |
| 2 | 010 |
| 1 | 001 |
Combine Binary Digits: Combine the binary equivalents: (0100001001)
Result: Octal of 2021 is equivalent to Binary 0100001001.
Conclusion
Octal numbers (base-8) are sort of the middle ground between the binary system (base-2) computers use and the decimal system (base-10) humans use.
Computers work with binary systems but strings of just 0 and 1 can be too long and unstructured for us. Binary to octal conversion makes it possible to compress these long strings and makes them easier to work with.
The octal system was more practical in the days of the first commercially successful minicomputer, the 12-bit PDP-8. A 12-bit binary string could easily be represented as a 4-digit octal number for convenience and brevity.
The adoption of octet characters/bytes made the hexadecimal number system more attractive with time. The hexadecimal number system can easily be used to represent bytes and 16/32/64-bit numbers with fewer digits.