What are Multidimensional Arrays in C++?

Introduction

Multidimensional array means an array of an array, that array now can be a 2D array, a 3D array, a 4D array, or an N-dimensional array. We are already familiar with 1D arrays, they are simply a collection or a list of similar types of data elements, and the data there in the 1D array is stored in a linear format, like a straight line. But when we talk about multi-dimensional arrays, actually they are also stored in a linear way only inside the memory, but the way we would visualize them will be a little different, here specifically if we talk about 2D arrays, then we can visualize them in the form of a table having certain rows and columns, and if we want to think of 3D arrays, then we can visualize them like a cube shape, having elements listed along its length, breadth, and the height.

In simple words, multi-dimensional arrays mean, an array of arrays. For example - let's say there is an array int arr[] = {1, 2, 3};

Prerequisites

Here in this article, we will keep things very simple and easy to understand, but still, it is suggested and will be better if you are already somewhere familiar and have a basic understanding of the concept of arrays. Read about arrays in C++ here.

General Form of Representing a C++ Multidimensional Array

We can represent a c++ multidimensional array having N dimensions in the following way.

Here

• dataType - signifies what type of data the array will be storing
• arrayName - the identifier or name of the array
• size1, size2...sizeN - here the number 1, 2...N represents the number of dimensions the array is going to have, and the size1, size2...sizeN represents the size of each individual dimension.

Example

We can represent a 2D array in the following way

Representation of a 3D array

Representation of an N-dimensional array

Size of C++ Multidimensional Array

In the case of simple arrays ie. 1D arrays, we can easily calculate their size by multiplying the size of 1 element by the number of elements present in the array. Just like that, in the case of multi-dimensional arrays as well, to get the size of the array, we will multiply the size of 1 element by the total number of elements present in the given array, now how will we get the total number of elements in a multi-dimensional array? For that, we can simply multiply the size of all the dimensions by each other.

Example

Suppose there is an array int arr2D[2][3];, now what is its size? we know that a multi-dimensional array is nothing but an array of arrays, here also the array arr2D is an array, of two 1D arrays. And each 1D array has 3 elements within it, now what will be the size of the arr2D here? 3 elements of the first 1D array and 3 elements of the second 1D array, a total of 6 elements, hence the number of elements in the arr2D will be 2*3 = 6 elements, and now talking about size, as the array here is an integer array and each int is of 4bytes, and there are a total 6 integers present in here, so its size will be 6*4 = 24bytes.

Two-Dimensional Arrays

About

Two-dimensional arrays are the simplest form of multi-dimensional arrays, we can visualize them as an array of a 1D array.

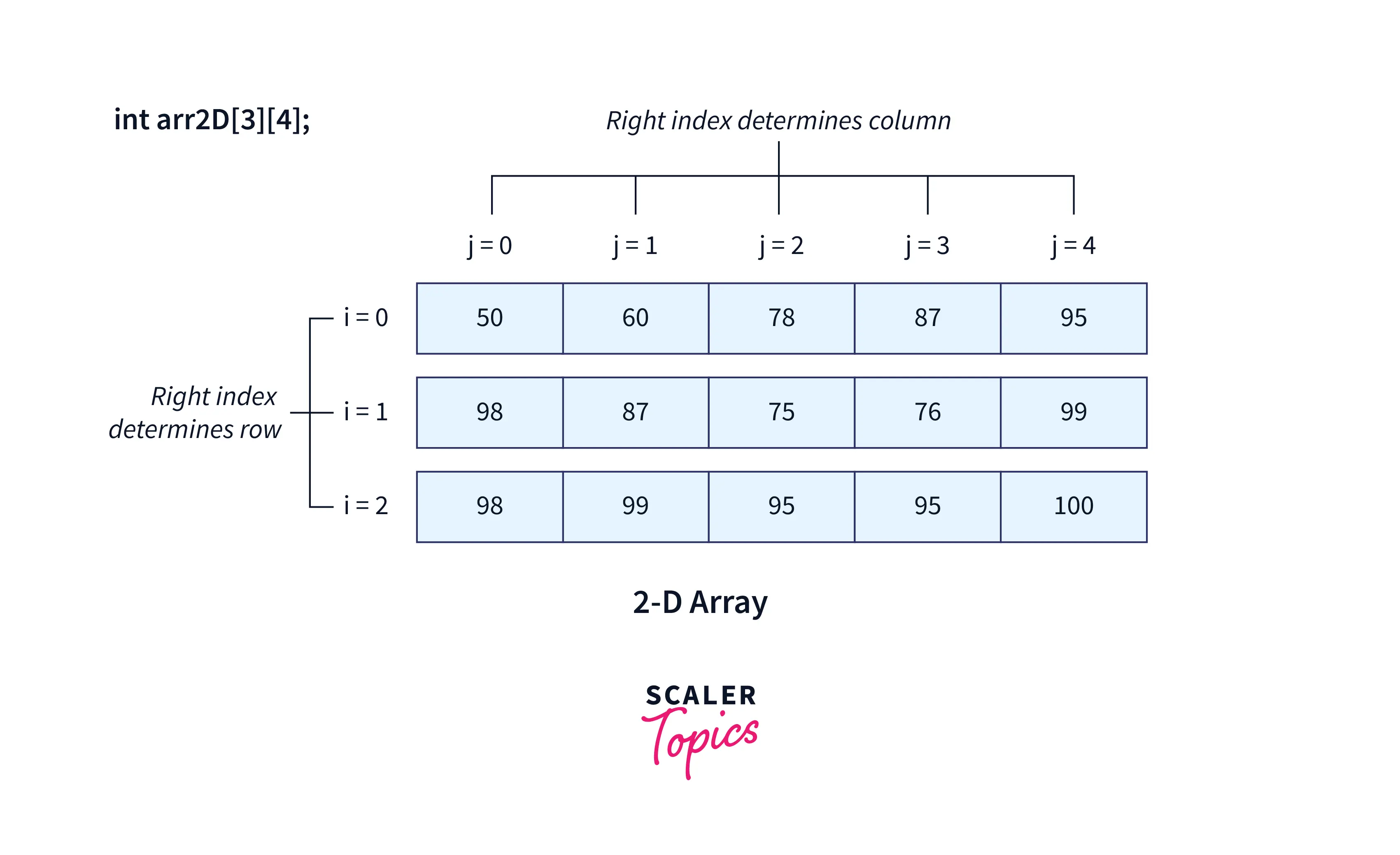
In the above image, we can see that 2D arrays are a table-like structures with certain rows and columns, where each row represents individual 1D arrays, and all these rows when grouped ie. when are arranged like an array again, they form the 2D array, and this is how 2D arrays can be seen as an array of 1D arrays.

Syntax

Let's have a look at its syntax

Declaration

We can declare a 2D array in the following way

Elements in 2D arrays are commonly represented as arr2D[i][j], where i is the row number and j is the column number.

Methods of Initialization

There are various through which we can initialize 2D arrays

1. Direct Assignment

In the above array, we have 2 rows and 3 columns, the elements that are listed here, will be placed in the array in the following way, the first 3 elements from the left will be in the first row, and the remaining 3 elements will be in the second row, if some more rows have had been there, then they would have got stored in the subsequent third, fourth and so on rows. This method works but is slightly confusing, we also have a visually better way using which we can initialize the array

2. Assignment by Breaking the Array into Sub-units

Here as well we are assigning the array its values, but instead of writing each value directly, we are separating them into some units, where each unit represents a 1D array, hence making the assignment appear more readable.

3. Assignment by taking user input

Here with the help of loops, we are asking the user to enter the array elements, in here we have an outer for loop which will define the row number in which the entered element will be stored, and the inner loop which will determine the exact position or index in that specific row to store the entered element.

4. Assignment using Dynamic Allocation

Here we are dynamically creating a 2D array, first of all, we are dynamically creating a 2D array, meaning an array of a 1D array that has two elements(two 1D arrays), then we are iterating for loop for the number of rows in that array, and inside that iteration, we are again dynamically creating an integer array which will consist of each element, and after that, we are having a for loop again to take the user input and to store that the correct location.

Accessing Elements in 2D Arrays

We can access an element in a 2D array with the help of that element's location, and how will we get the location? each element in an array is stored at a specific position, meaning the location at which an element has been stored would be part of a certain row right? and a certain column as well, now clubbing these two, will let us access the element stored at that location.

For example -

In the above example, the syntax written represents, the element stored in the second row and the third column.

Note - As the array indices start from 0, due to which an array with an N number of rows will have rows numbered from 0 to N-1, this is why when in the above example, the row number is written as 1, we called it the second row, because the first row will be arr2D[0][j];, similarly for the columns as well.

Example

Let's understand the above concepts with the help of an example

Output

Three-Dimensional Arrays

About

Three-dimensional or 3D arrays can be visualized as an array or a list of 2D arrays, and 2D arrays in themselves are the array of 1D arrays, meaning they are the same as what we understand of 2D arrays, their 2D arrays contain a list of 1D arrays, here 3D arrays contain a list which again contains a list of 1D arrays.

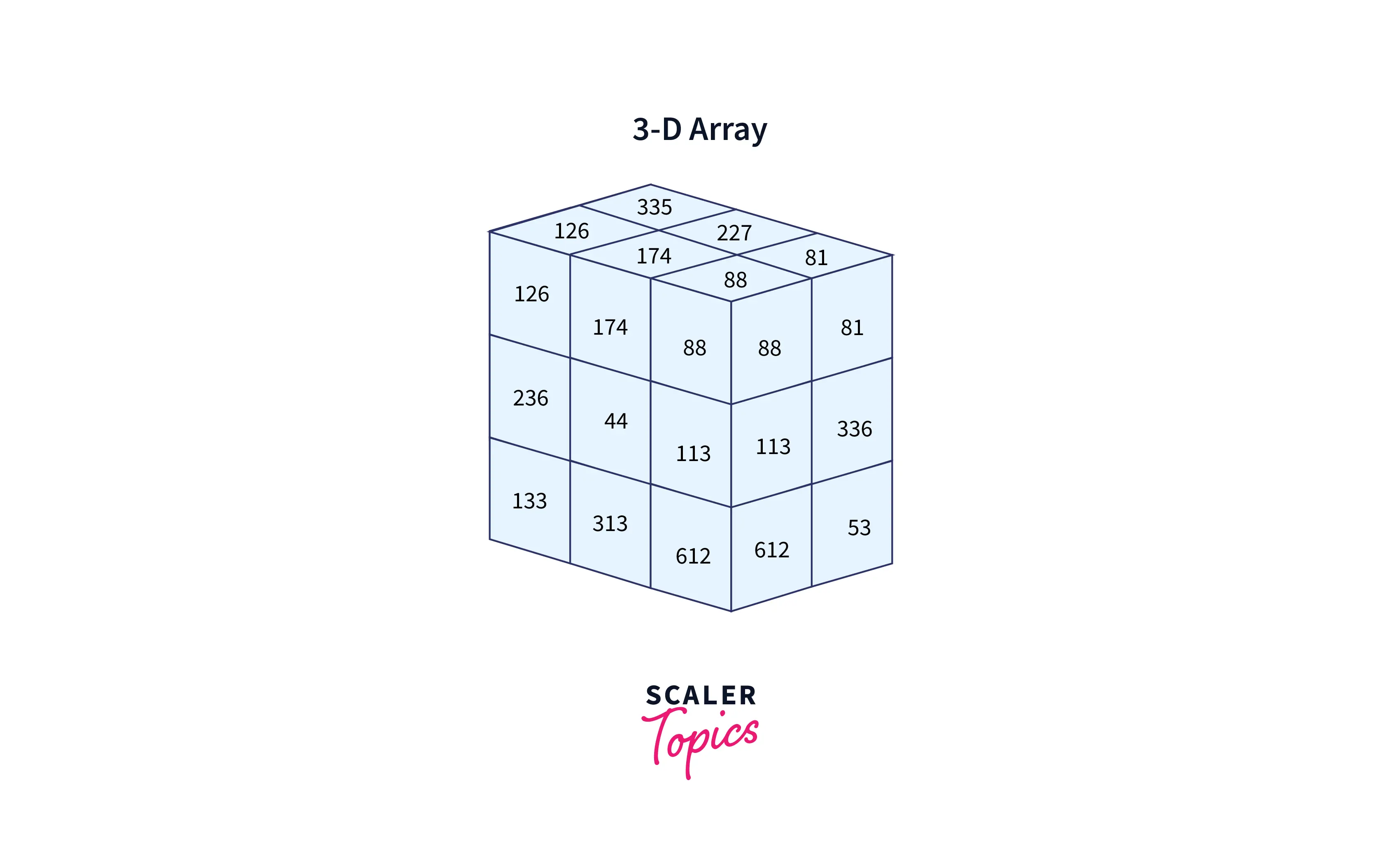
In the above image, we can see that 3D arrays are nothing more than a collection of 2D arrays. And we know that 2D arrays can be referred to as a table, so 3D arrays are simply just another form of a container that contains those tables, simple?

Syntax

Let's have a look at its syntax

Declaration

We can declare a 3D array in the following way

Elements in 3D arrays are commonly represented as arr3D[i][j][k], where i is the layer number, j is the row number of that specific layer and k is the column number of that layer.

Methods of Initialization

1. Direct Assignment

In the above array, we have 2 layers, 3 rows, and 4 columns, the elements that are listed here, will be placed in the array in the following way, as there is a total of 2*3*4 = 24 elements in the above array, now look at the left-most dimension, which specifies the number of layers, its 2 here, meaning the above array will have 2 layers, now 24 elements in 2 layers, meaning each layer will have 12 elements. Now we understood that each layer here will have 12 elements, meaning the first 12 elements will be stored in layer 1, and the remaining 12 elements will be stored in layer 2, and talking about each layer, as each layer has 3 rows, now 12 elements in 3 rows, meaning each row will have 4 elements, as specified by the number of columns, and in this way, the elements given here will be stored in the memory.

This method works like 2D arrays but is more confusing now, let's divide the initialization into sub-units for better understanding.

2. Assignment by breaking the Array into sub-units

Here as well we are assigning the array its values, but instead of writing each value directly, we are separating them into several sub-units, where the first sub-unit determines the layer number of the 3D array, and the sub-unit inside every layer determines the row number of that layer, and each individual entry inside the row represents the individual elements and hence making it more readable.

3. Assignment by taking user input

In this method, we are asking the user to enter the array elements, in here we first have an outermost loop to define the layer number in which the entered element will be stored, and then a child loop of its to determine the row number of that specific layer, and one more child loop inside that loop which will determine the exact position or index in that particular row where the entered element will be stored.

Accessing Elements in 3D Arrays

We can access an element in a 3D array same as we do in the case of 2D arrays, by getting that element's location, and how will we get that here? we would be needing three loops in the case of 3D arrays, the first to specify the layer number, the second loop will tell the row number in that specific layer, and the third loop will tell the position or index of that specific element.

For example -

In the above example, the syntax written represents the element stored in the first layer, in the third row, and in the fifth column position.

Example

Let's understand the above concepts with the help of an example

Output

How to Create N-Dimensional Array

Just like we have created 2D and 3D arrays, we can even create 4D, 5D, and so on dimensionally vast arrays, but we need to remember along with the increasing number of dimensions the complexity to manage the array will also increase.

The most used multi-dimension arrays are 2D and 3D arrays, even among these two, the most used arrays are 2D arrays.

More Examples of C++ Multidimensional Arrays

1. Changing Elements in a C++ Multidimensional Array

We know that we can overwrite elements in a 1D array, just like that, we can do the same in the case of multi-dimensional arrays as well. Let's have a look at the below example

Output

2. Practical Implementation of C++ Multidimensional Arrays - Mini Archer game

Output

Related Articles

You may want to read Arrays in C++.