CRC Program in C

During data transmission, digital signals may undergo noise, leading to errors in the received data. Detecting and preventing errors is crucial, and Cyclic Redundancy Check (CRC) is an error detection technique in C programming. Understanding CRC in C is essential for writing robust software. This article comprehensively covers the nature, operation, and applications of CRC, providing insights into real-world scenarios. Whether a beginner or experienced programmer, this article is a valuable resource for learning the CRC program in C and enhancing error-checking capabilities in software development.
Understanding the Theory Behind CRC
Cyclic Redundancy Check is an error detection algorithm used to check the validity of the data sent by the sender. In CRC, in addition to the data to be transmitted, the algorithm requires a generator polynomial that is used to compute the check value using binary division. The check value or the CRC is sent along with the data to the receiver to check the validity of the data.
The data that is to be sent to the receiver can be represented in the polynomial form with the degree of the polynomial as the bit positions. For example, the binary data 1010101 of length 7 can be represented as,
The bit value of 0 is not represented as the value of that representation is also 0.
The generator polynomial can also be represented in binary. The degree of the generator polynomial must be greater than 0 and lesser than the degree of the data. The CRC can be classified into different standards based on the degree of the generator polynomial. The CRC-8 standard use a generator polynomial of degree 8 and CRC-16 uses a generator polynomial of degree 16. A simple representation of the generator polynomial is given as follows.
The above generator polynomial is represented in binary data as 00011010.
Note : Cyclic Redundancy Check can also be used as a hashing function and in such cases, the CRC-8 standard is not used as it can produce only 256() values.
The steps involved in CRC are as follows, In the sender side,
- The data of length, n, and the generator polynomial of length, l is prepared.
- The data to be sent is appended with (l-1) number of zeros.
- Binary division is performed with the data as dividend and the binary equivalent of the generator polynomial as the divisor. The remainder of the binary division is the check value.
- The signal is sent with the check value appended to the end of the data.
The mathematical representation of check value or CRC is,
Here, the n represents the number of bits in the generator polynomial On the receiver side,
- The data received again proceeds with binary division with the data as dividend and the binary equivalent of the generator polynomial as the divisor.
- If the remainder of the binary division is zero then the data transmitted from the sender has no error. If the remainder is not zero, then the signal has been corrupted with an error.
The process of binary division follows the following steps and is similar to normal polynomial division,
- Each step of the division involves XOR of divisor and dividend. The first n bits of the divisor are only used for this operation where n is the number of bits in the dividend.
- The quotient will be 1 or 0 based on the n-bit data. If the last bit of the data is 1, then the quotient is 1 and if the last bit of the data is 0, then the quotient is 0.
- Then the bit at the position n+1 is taken from the data and appended with the remainder of the above operation. This remainder becomes the divisor for the next operation.
- The operation is repeated until all the bits in the data are used in the calculation.
The above procedure can be one of the interesting properties followed by the Cyclic Redundancy Check is, CRC(x^y^z) == crc(x) ^ crc(y) ^ crc(z).
The ^ symbol represents the XOR function. If we perform an XOR on 3 data and perform a CRC on the result, then the result of the CRC will be equivalent to CRC on the individual data and XOR with the results. CRC can be used as
Note : The XOR operator returns 0 when both the inputs are the same and returns 1 in other cases.
Examples for Better Understanding
Let us consider the following example to understand how error checking is performed using Cyclic Redundancy Check.
Let the data be 1001101 and the binary equivalent of the generic polynomial is 1011. On the sender side, the remainder can be found using binary division as follows,
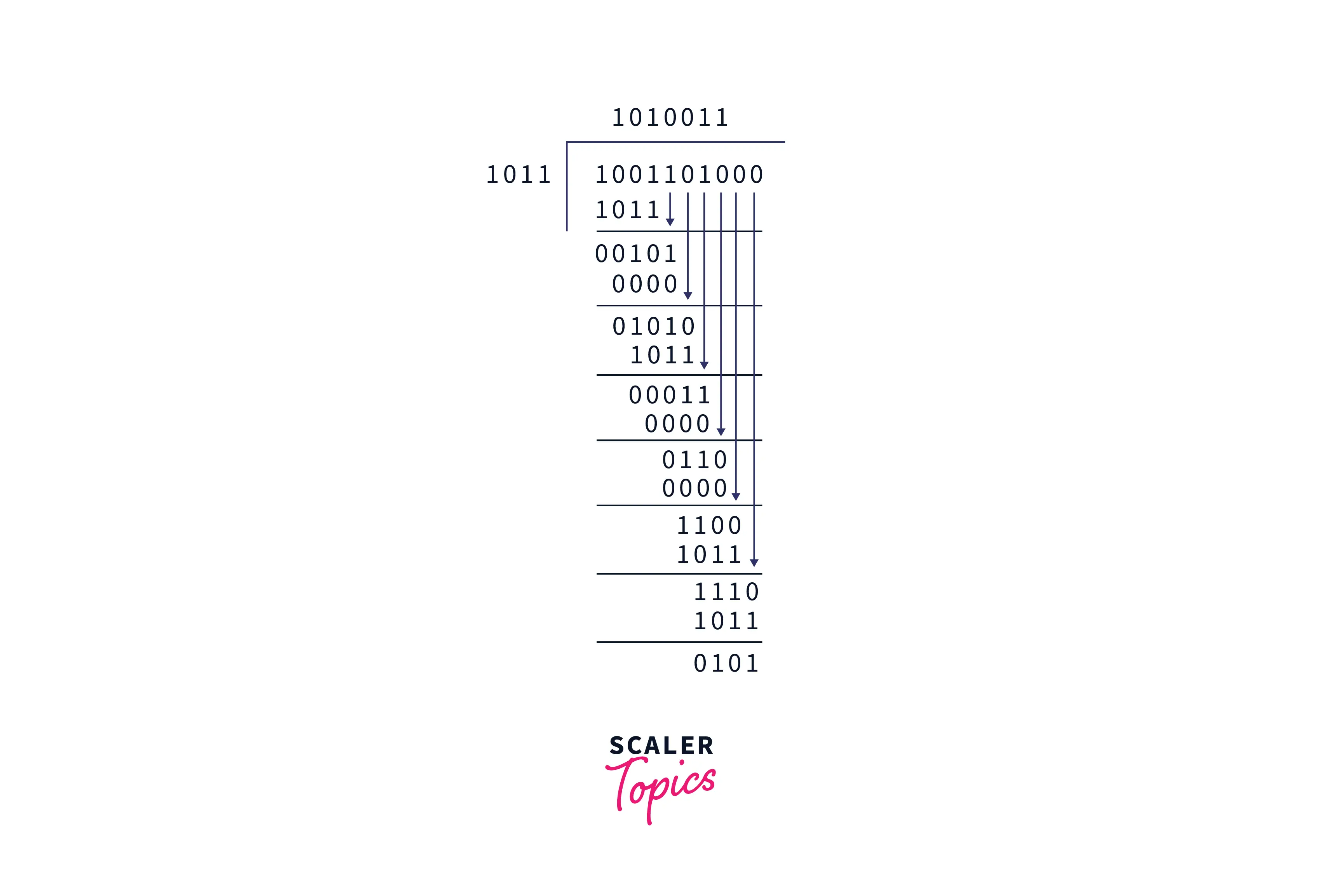
The remainder of the above division is 101. This remainder is appended to the data to create the signal which will be sent to the receiver. The signal is 1001101101.
Then error checking is performed on the receiver side as follows,

As the remainder is 0, we can assure that there is no error in the received message.
Let us now consider the case, in which the message received is 1001001101 in which the 6th bit from last is inverted.
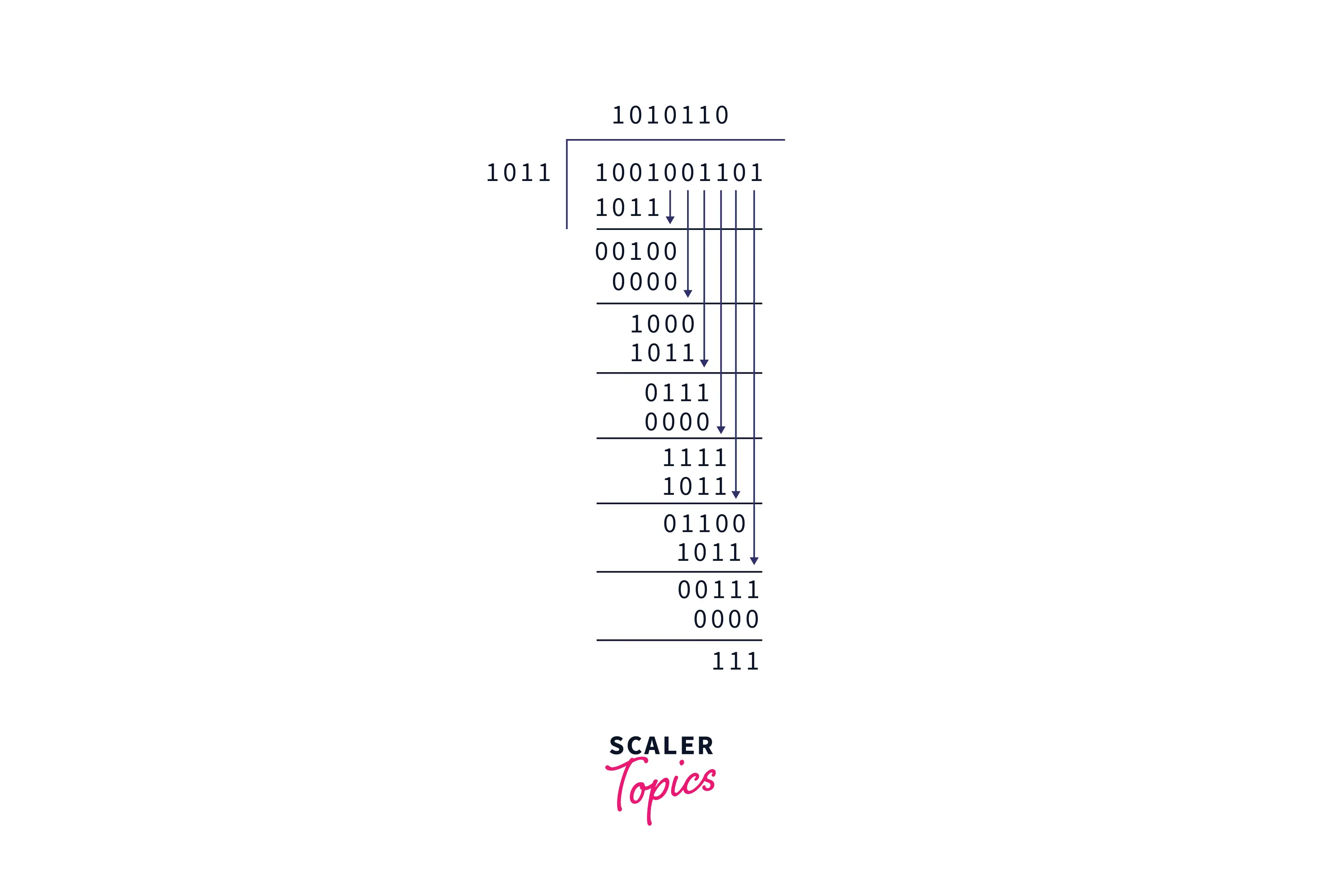
As the remainder is 111, we can assure that there is an error in the message.
Implementation for CRC in C
There are two methods to implement the CRC program in the C programming language. The first method uses a character array and the next method uses bit manipulation techniques.
Algorithm
The algorithm used to implement the CRC program in C is as follows,
- Get the data and generator polynomial.
- Let n be the length of the generator polynomial.
- Append n-1 zeros to data.
- Call the CRC function.
The algorithm used in the CRC function is as follows,
- Get the first n bits from the data.
- If the first bit is 1, then perform a xor operation with the first n bits of data and the generator polynomial.
- Shift the bits by 1 position to leave the first bit.
- Append a bit from the data. Repeat the process until all the bits in the data are appended.
The algorithm used in the XOR function is based on the following truth table of the XOR operator,
| Operand 1 | Operand 2 | Output(^) |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
- The first bit is compared with the second bit and if both the bits are the same, then the output is 0.
- If the bits are different, then the output is 1.
The algorithm used to check for errors on the receiver side is as follows,
- The data received again proceeds with a Cyclic Redundancy Check to find the remainder.
- The remainder is iterated with conditions that there must be no 1 in the remainder and the length of the remainder must be lesser than the generator polynomial.
- If all the elements are iterated, we can assure that there is no error, else there is error.
Code
Let us see the program for the implementation of CRC in C
- The strlen() function is used to find the length of a character array. The string.h header must be included to use this function.
Output:
As the data transmitted and received are the same, &&there is no error** in the signal.
In the case of error,
Since the data send is different from the data received, there is an error in the signal.
Complexity
The time complexity and space complexity are used to represent the execution time and space required by the program. The time and space complexities are expressed using the Big-O notation. Since there are two for loops implied at a time, the time complexity of the program is O(). The space complexity of the program is O(n) and is due to the single dimension character array used to store n characters.
Implementation for CRC using Bit Manipulation
This method of implementing the CRC program in C uses bit manipulation techniques.
Algorithm
The algorithm used to implement CRC in C using bit manipulation is as follows,
- Get the data and generator polynomial.
- Convert both the data and generator polynomial to decimal values.
- Shift the bits in data by n-1 positions to append zeros at the end of data, where n is the length of the generator polynomial.
- Find the number of bits to be shifted using the logarithmic function.
- Shift the data by the computed number of bits and perform XOR operation with generator polynomial.
- Find the remainder of the operation and append a bit of data to the remainder for further computation.
- Repeat the process until all bits in data are utilized in the computation.
The algorithm used to convert decimal values to binary values is as follows,
- Find the remainder by performing a modulo operation with the number and 2.
- Find the value of 10 raised to the power of count and multiply it with the remainder.
- Sum the value found as a result of the previous step.
- Divide the decimal by 2 and increment the counter. Repeat the steps until the decimal becomes is not equal to 0.
Let us consider an example of converting the decimal 5 to binary and walkthrough each step,
| Variables | STEP1 1 | STEP 2 | STEP 3 |
|---|---|---|---|
| count | 0 | 1 | 2 |
| rem | 1 | 0 | 1 |
| tmp | 1 | 10 | 100 |
| binary | 1 | 1 | 101 |
| decimal | 2 | 1 | 0 |
The algorithm used to convert binary values to decimal equivalent is as follows,
- If the bit value is 1, then find the value of that position by shifting the bits from the decimal number one by the required number of positions.
For example, consider the binary value 0010, then the decimal equivalent can be found by shifting the decimal number one by 1 position, 0001 << 1 => 0010 which has a value of 3.
Code
- The log2l() function is used to find the logarithmic to the base 2 for a number and has the following syntax,
The function returns the logarithmic value as a type of long double
- The ceill() function is used to round the value to the nearest maximum number. The syntax for the function is,
For example, if the value is 6.25, then ceill(6.25) will return the value of 7.00.
- The operators << and >> are called bit shifting operators and are used to shift bits in the left and right direction.
- The operator & is called the bitwise AND operator and is used to perform AND operation between two numbers and the | is called the bit wise OR operator and is used to perform OR operation between two numbers.
Let us consider an example sample implementation of the CRC function with the input data as 1001101 and the generator function as 1011,
Note : The log to the base 2 functions is used to find the number of bits present in the data. The general definition of log base 2 is to find the power of 2 needed to get the value of n, where n is the number given as input to the function. The ceill() function is used along with the log base 2 functions to find the number of bits which is then used to find the number of bits to shift.
Output:
Complexity
The time complexity and space complexity are used to represent the execution time and space required by the program. The Big-O notation is used to express the complexity of the program. Since only one for loop is implied at a time, the time complexity will be O(n) and the space complexity of the program is O(n) and is due to the single dimension character array used to store the characters.
Conclusion
- Cyclic Redundancy Check is an error validation algorithm used to check if there is any error in the signal transmitted by the sender.
- A generator polynomial is used to find the CRC value of the data and the data is transmitted along with the CRC.
- The XOR operation is performed at each step of the process to find the value of CRC.
- Validation is performed at the receiver side by checking if the CRC calculated on the receiver side is equal to zero.
- The implementation of the CRC program in C can be done either by using a character array or by using the bit manipulation technique.
- The time and space complexity of both algorithms is the same.
