Apriori Algorithm in Data Mining

Introduction to Apriori Algorithm

The Apriori algorithm in data mining is a widely used algorithm to find frequent itemsets in a dataset. The Apriori algorithm is used to implement frequent pattern mining (FPM). Frequent pattern mining is a data mining technique to discover frequent patterns or relationships between items in a dataset. Frequent pattern mining involves finding sets of items or itemsets that occur together frequently in a dataset. These sets of items or itemsets are called frequent patterns, and their frequency is measured by the number of transactions in which they occur.

In data mining, an itemset is a collection of one or more items that appear together in a transaction or dataset. An itemset can be either a single item, also known as a 1-itemset, or a set of k items, also known as a k-itemset. For example, in sales transactions of a retail store, an itemset can be referred to as products purchased together, such as bread and milk, which would be a 2-item set. The Apriori algorithm can be used to discover frequent itemsets in the sales transactions of a retail store. For instance, the algorithm might discover that customers who purchase bread and milk together often also purchase eggs. This information can be used to recommend eggs to customers who purchase bread and milk in the future.

The Apriori algorithm is called "apriori" because it uses prior knowledge about the frequent itemsets. The algorithm uses the concept of "apriori property," which states that if an itemset is frequent, then all of its subsets must also be frequent.

Apriori Property

The Apriori property is a fundamental property of frequent itemsets used in the Apriori algorithm. In other words, if an itemset appears frequently enough in the dataset to be considered significant, then all of its subsets must also appear frequently enough to be significant. For example, if the itemset {A, B, C} frequently appears in a dataset, then the subsets {A, B}, {A, C}, {B, C}, {A}, {B}, and {C} must also appear frequently in the dataset.

The Apriori property allows the Apriori algorithm in data mining to efficiently search for frequent itemsets by eliminating candidate itemsets containing infrequent subsets, as they cannot be frequent. This search space pruning reduces the time and memory required to find frequent itemsets in large datasets.

Apriori Algorithm Components

Before getting into the steps involved in the Apriori algorithm, let’s understand the various terminologies used in the Apriori algorithm.

Support

In the Apriori algorithm, support refers to the frequency or occurrence of an item set in a dataset. It is defined as the proportion of transactions in the dataset that contain the itemset. For example, let's consider a dataset of sales transactions in a retail store that contains the following items - milk, bread, cheese, eggs, butter, and yogurt. To calculate the support of an itemset, we count the number of transactions in which the itemset appears and divide it by the total number of transactions in the dataset. For instance, if the itemset {milk, bread} appears in 5 transactions out of 10 transactions in the dataset, then its support is $5/10 = 0.5$, or 50%.

In the Apriori algorithm, itemsets with a support value above the minimum defined support threshold are considered frequent and are used to generate candidate itemsets for the next iteration of the algorithm.

Lift

Lift measures the strength of the association between two items. It is defined as the ratio of the support of the two items occurring together to the support of the individual items multiplied together. Lift for any two items can be calculated using the below formula -

If the lift value is greater than 1, then it indicates a positive association between the two items, which means that the two items are more likely to be bought together. A lift value of exactly 1 indicates that the two items are independent and there is no association between the two items, while a value less than 1 indicates a negative association, meaning that two items are more likely to be bought separately.

Confidence

In the Apriori algorithm, confidence is also a measure of the strength of the association between two items in an itemset. It is defined as the conditional probability that item B appears in a transaction, given that another item A appears in the same transaction. Support for two items can be calculated using the below formula.

If the confidence value exceeds a specified threshold, it indicates that item B is likely to be purchased with item A. For instance, if the confidence of the association between "bread" and "butter" is 0.8, it means that when a customer buys "bread", there is an 80% chance that they will also buy "butter". This can be useful in recommending to customers or optimizing product placement in a store.

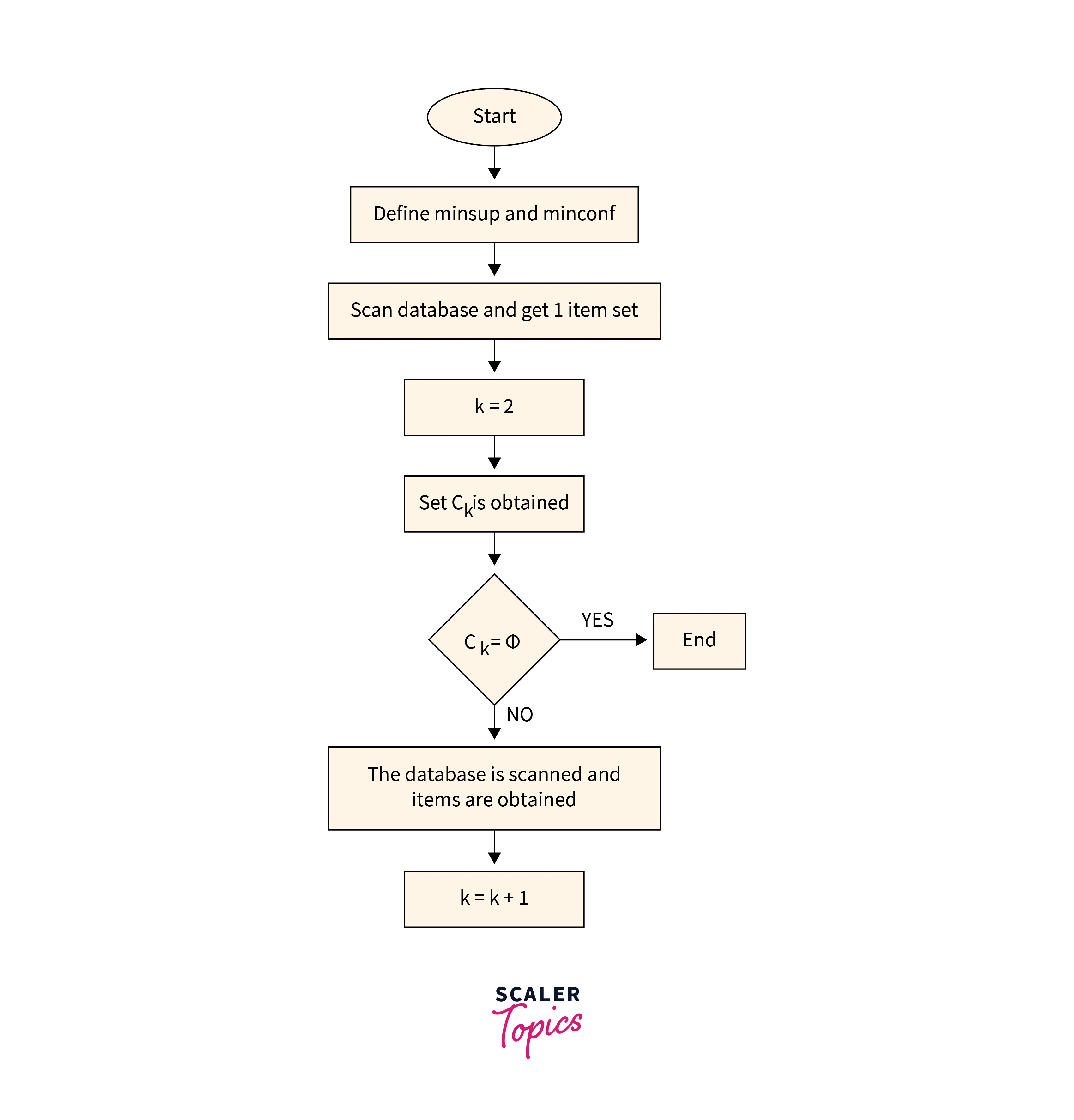
Steps in Apriori Algorithm

Here are the steps involved in implementing the Apriori algorithm in data mining -

1. Define minimum support threshold - This is the minimum number of times an item set must appear in the dataset to be considered as frequent. The support threshold is usually set by the user based on the size of the dataset and the domain knowledge.
2. Generate a list of frequent 1-item sets - Scan the entire dataset to identify the items that meet the minimum support threshold. These item sets are known as frequent 1-item sets.
3. Generate candidate item sets - In this step, the algorithm generates a list of candidate item sets of length k+1 from the frequent k-item sets identified in the previous step.
4. Count the support of each candidate item set - Scan the dataset again to count the number of times each candidate item set appears in the dataset.
5. Prune the candidate item sets - Remove the item sets that do not meet the minimum support threshold.
6. Repeat steps 3-5 until no more frequent item sets can be generated.
7. Generate association rules - Once the frequent item sets have been identified, the algorithm generates association rules from them. Association rules are rules of form A -> B, where A and B are item sets. The rule indicates that if a transaction contains A, it is also likely to contain B.
8. Evaluate the association rules - Finally, the association rules are evaluated based on metrics such as confidence and lift.

Apriori Algorithm Example

Let’s try to understand the Apriori algorithm implementation using an example. In this example, we will use a minimum support threshold of 3. This means an item set must appear in at least three transactions to be considered frequent.

• Let’s consider the transaction dataset of a retail store as shown in the below table.

  TID	Items
  T1	{milk, bread}
  T2	{bread, sugar}
  T3	{bread, butter}
  T4	{milk, bread, sugar}
  T5	{milk, bread, butter}
  T6	{milk, bread, butter}
  T7	{milk, sugar}
  T8	{milk, sugar}
  T9	{sugar, butter}
  T10	{milk, sugar, butter}
  T11	{milk, bread, butter}

• Let’s calculate support for each item present in the dataset. As shown in the below table, support for all items is greater than 3. It means that all items are considered as frequent 1-itemsets and will be used to generate candidates for 2-itemsets.

  Item	Support (Frequency)
  milk	8
  bread	7
  sugar	5
  butter	7

• Below table represents all candidates generated from frequent 1-itemsets identified from the previous step and their support value.

  Candidate Item Sets	Support (Frequency)
  {milk, bread}	5
  {milk, sugar}	3
  {milk, butter}	5
  {bread, sugar}	2
  {bread, butter}	3
  {sugar, butter}	2

• Now remove candidate item sets that do not meet the minimum support threshold of 3. After this step, frequent 2-itemsets would be - {milk, bread}, {milk, sugar}, {milk, butter}, and {bread, butter}. In the next step, let’s generate candidates for 3-itemsets and calculate their respective support values. It is shown in the below table.

  Candidate Item Sets	Support (Frequency)
  {milk, bread, sugar}	1
  {milk, bread, butter}	3
  {milk, sugar, butter}	1

• As we can see in the above table, only one candidate itemset exceeds the minimum defined support threshold - {milk, bread, butter}. As there is only one 3-itemset exceeding minimum support, we can’t generate candidates for 4-itemsets. So, in the next step, we can write the association rules and their respective metrics, as shown in the below table.

  Candidate Item Sets	Support (Frequency)
  {milk, bread}	{butter} (Confidence - 60%)1
  {bread, butter}	{milk} (Confidence - 100%)
  {milk, butter}	{bread} (Confidence - 60%)

• Based on association rules mentioned in the above table, we can recommend products to the customer or optimize product placement in retail stores.

Want to Explore Further? This Best Data Science Course Delivers In-Depth Insights Beyond the Blog. Enroll Now for a Rich Learning Experience!

Advantages and Limitations of Apriori Algorithm

Here are some of the advantages of the Apriori algorithm in data mining -

• Apriori algorithm is simple and easy to implement, making it accessible even to those without a deep understanding of data mining or machine learning.
• Apriori algorithm can handle large datasets and run on distributed systems, making it scalable for large-scale applications.
• Apriori algorithm is one of the most widely used algorithms for association rule mining and is supported by many popular data mining tools.

Below are some of the limitations of the Apriori algorithm in data mining -

• Apriori algorithm can be computationally expensive, especially for large datasets with many itemsets. For example, if a dataset contains $10^4$ from frequent 1- itemsets, it will generate more than $10^7$ 2-length candidates, which makes this algorithm computationally expensive.
• Apriori algorithm can generate a large number of rules, making it difficult to sift through and identify the most important ones.
• The algorithm requires multiple database scans to generate frequent itemsets, which can be a limitation in systems where data access is slow or expensive.
• Apriori algorithm is sensitive to data sparsity, meaning it may not perform well on datasets with a low frequency of itemsets.