Dimensionality Reduction in Data Mining

What is Dimensionality Reduction in Data Mining?

Dimensionality reduction in data mining refers to the process of reducing the number of features or variables in a dataset while preserving the essential information. For example, in a dataset with hundreds or thousands of features, dimensionality reduction techniques can help identify the most important features and discard the redundant ones.

The need for dimensionality reduction arises due to the curse of dimensionality, where the number of features in a dataset increases, and the difficulty in finding meaningful patterns and relationships also increases. This results in decreased efficiency and accuracy of data analysis algorithms. Hence, dimensionality reduction is required to reduce computational complexity, save storage space, and improve the performance of analysis techniques.

Also, as the number of features increases, the complexity of the ML model increases, leading to overfitting, reduced generalization, and decreased performance. Dimensionality reduction techniques such as Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), or t-Distributed Stochastic Neighbor Embedding (t-SNE) can mitigate these issues.

Dimensionality reduction is widely used in various domains, such as image processing, signal processing, bioinformatics, text classification, and recommendation systems.

The Curse of Dimensionality

The curse of dimensionality is a phenomenon in which the performance of machine learning algorithms deteriorates as the number of features or dimensions increases. This occurs because the volume of the data space grows exponentially with the number of dimensions, making it increasingly difficult to find meaningful patterns or relationships in the data.

As the number of dimensions increases, the data points become increasingly sparse, and the distance between them grows, making it challenging to classify or cluster them accurately. This can lead to overfitting, reduced generalization, and decreased model performance.

To mitigate the curse of dimensionality, dimensionality reduction techniques can be used. These methods help to reduce the number of dimensions while retaining the most relevant information, thereby improving the performance of machine learning algorithms.

Why is Dimensionality Reduction Important?

Dimensionality reduction is an essential technique in machine learning, data mining, and other related fields, as it offers several benefits, including -

• Improved performance:
  High-dimensional data can be computationally expensive and can lead to overfitting, which can result in reduced accuracy and generalization of machine learning models. Dimensionality reduction can reduce computational complexity and improve model performance.
• Data visualization:
  Dimensionality reduction techniques can help visualize high-dimensional data in two or three dimensions, which makes it easier to interpret and understand complex datasets.
• Feature selection:
  Dimensionality reduction can help identify the most important features in a dataset, which can be useful for feature selection, reducing noise, and improving the accuracy of machine learning models.
• Reduced storage:
  High-dimensional datasets require more storage space, which can be expensive and impractical. Dimensionality reduction techniques can reduce the storage space required to store data.
• Improved efficiency:
  By reducing the number of features, dimensionality reduction can make data mining and machine learning algorithms more efficient, reducing processing time and computation costs.

Components of Dimensionality Reduction

Dimensionality reduction techniques can be broadly classified into two categories based on the approach used:

Feature Selection

This approach selects a subset of the original features or variables, discarding the rest. Feature selection methods can be further divided into three categories -

• Filter methods:
  These methods evaluate the relevance of each feature independently of the target variable and select the most relevant ones based on a specific criterion, such as correlation or mutual information. A few of the most common filter methods include Correlation, Chi-Square Test, ANOVA, Information Gain, etc.
• Wrapper methods:
  These methods evaluate the performance of a model trained on a subset of features and select the best subset based on model performance. Some of the wrapper methods include forward selection, backward selection, bi-directional elimination, etc.
• Embedded methods:
  These methods combine feature selection with model training, selecting the most relevant features during the training process. Some commonly used embedded methods include LASSO, Ridge Regression, etc.

Feature Extraction

This approach transforms the original features into a new set of features, typically of lower dimensionality, while preserving the most important information. Feature extraction methods can be further divided into two categories:

• Linear methods:
  These methods transform the data using linear transformations, such as Principal Component Analysis (PCA) or Linear Discriminant Analysis (LDA).
• Non-linear methods:
  These methods use non-linear transformations to map the data to a lower-dimensional space, such as t-Distributed Stochastic Neighbor Embedding (t-SNE) or Autoencoders.

Common Techniques of Dimensionality Reduction

A few of the most commonly used techniques of dimensionality reduction in data mining include the following:

Principal Component Analysis (PCA)

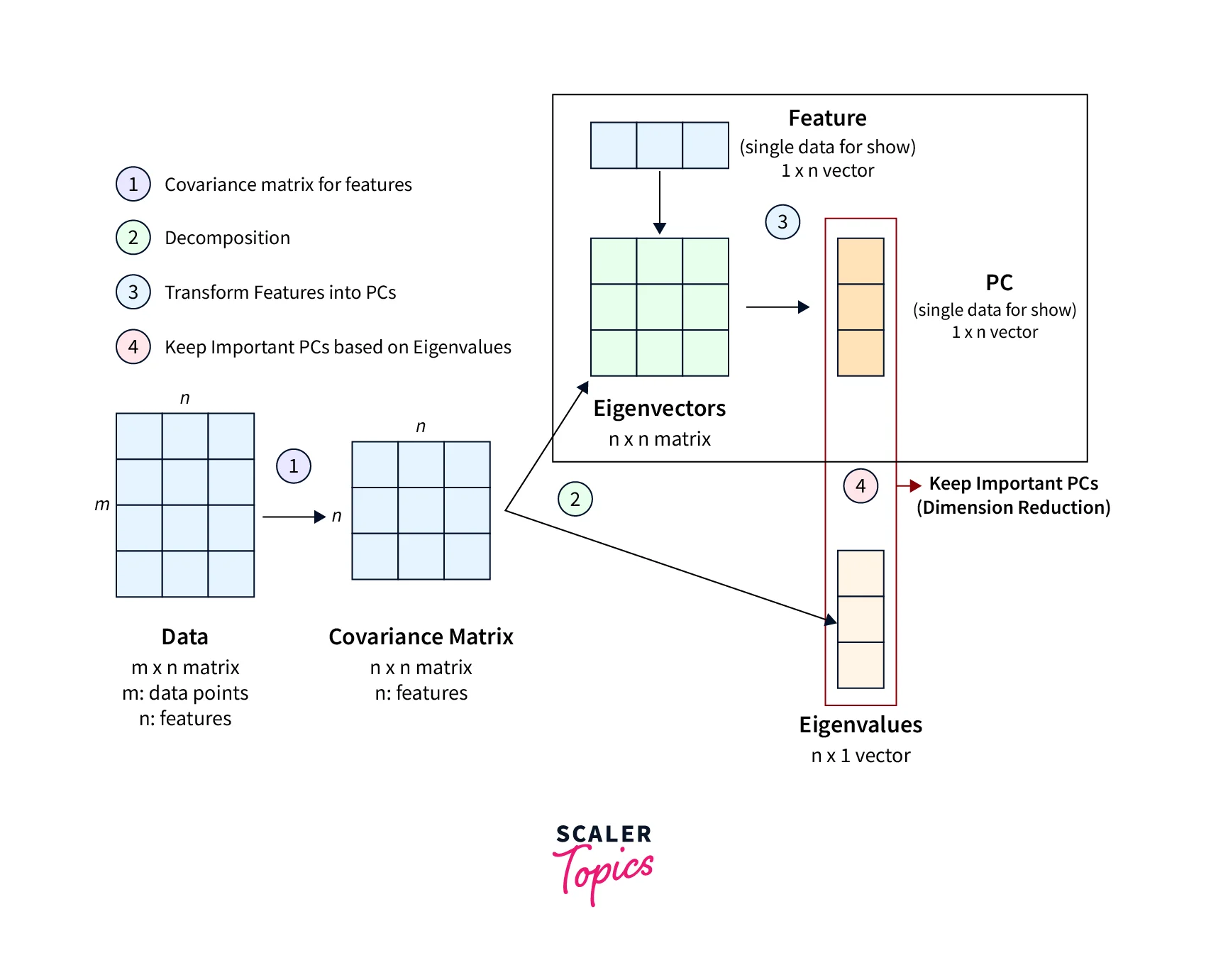
PCA is a linear dimensionality reduction technique that transforms high-dimensional data into a lower-dimensional space by identifying the principal components of the data. These principal components are orthogonal vectors that capture the maximum amount of variance in the data. By selecting a subset of these principal components, PCA can reduce the dimensionality of the data while retaining most of its variance.

Linear Discriminant Analysis (LDA)

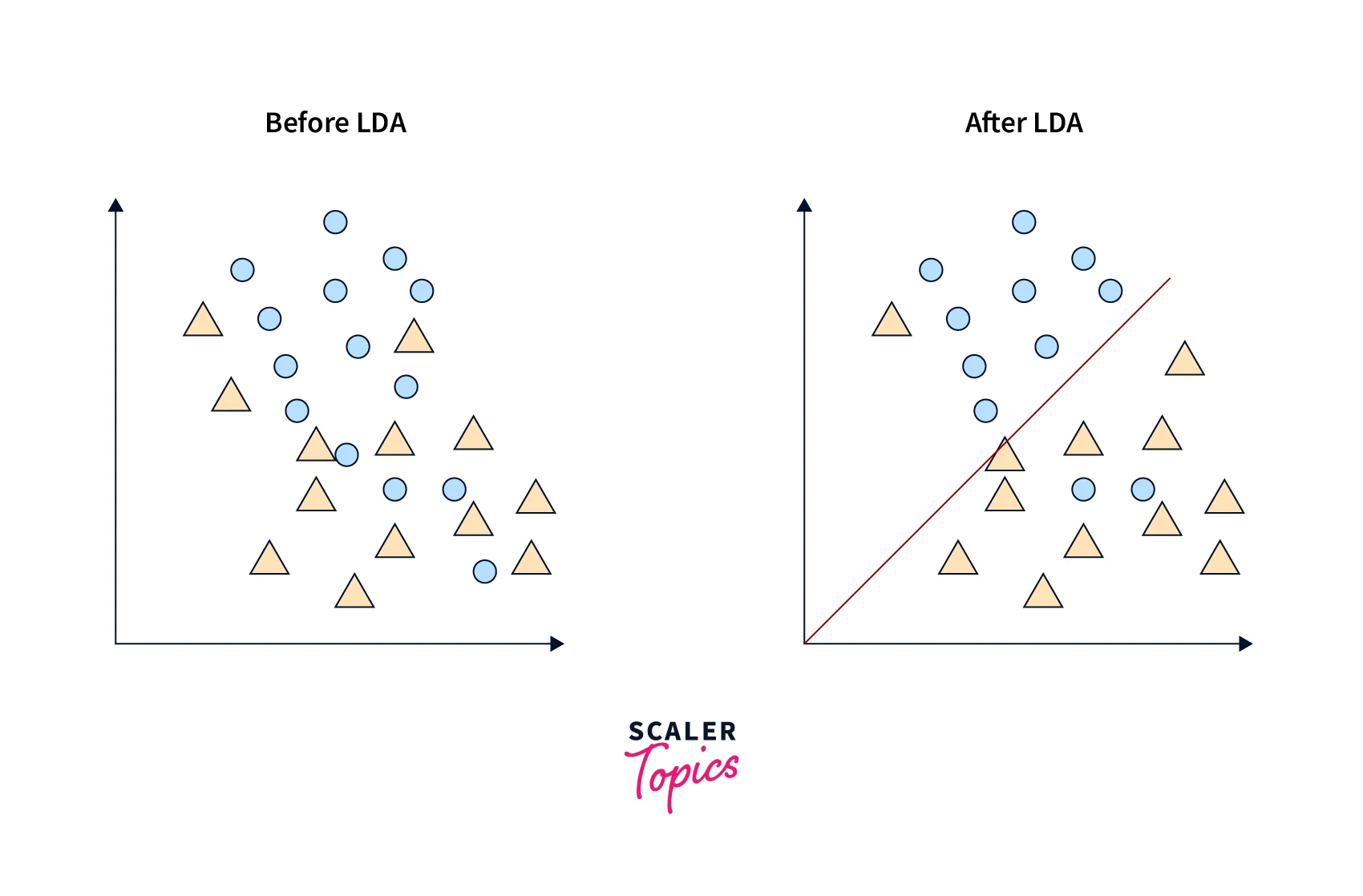
LDA is another linear dimensionality reduction technique, but it is primarily used for supervised classification tasks. LDA aims to identify the features that best separate the classes in the data by maximizing the ratio of between-class variance to within-class variance. By selecting a subset of these features, LDA can reduce the dimensionality of the data while preserving the class separation.

t-Distributed Stochastic Neighbor Embedding (t-SNE)

t-SNE is a non-linear dimensionality reduction technique that is primarily used for visualization purposes. It aims to map high-dimensional data onto a low-dimensional space while preserving the pairwise similarities between data points. t-SNE achieves this by modeling the similarities in the high-dimensional space using a Student's t-distribution and the similarities in the low-dimensional space using a Gaussian distribution.

Autoencoders

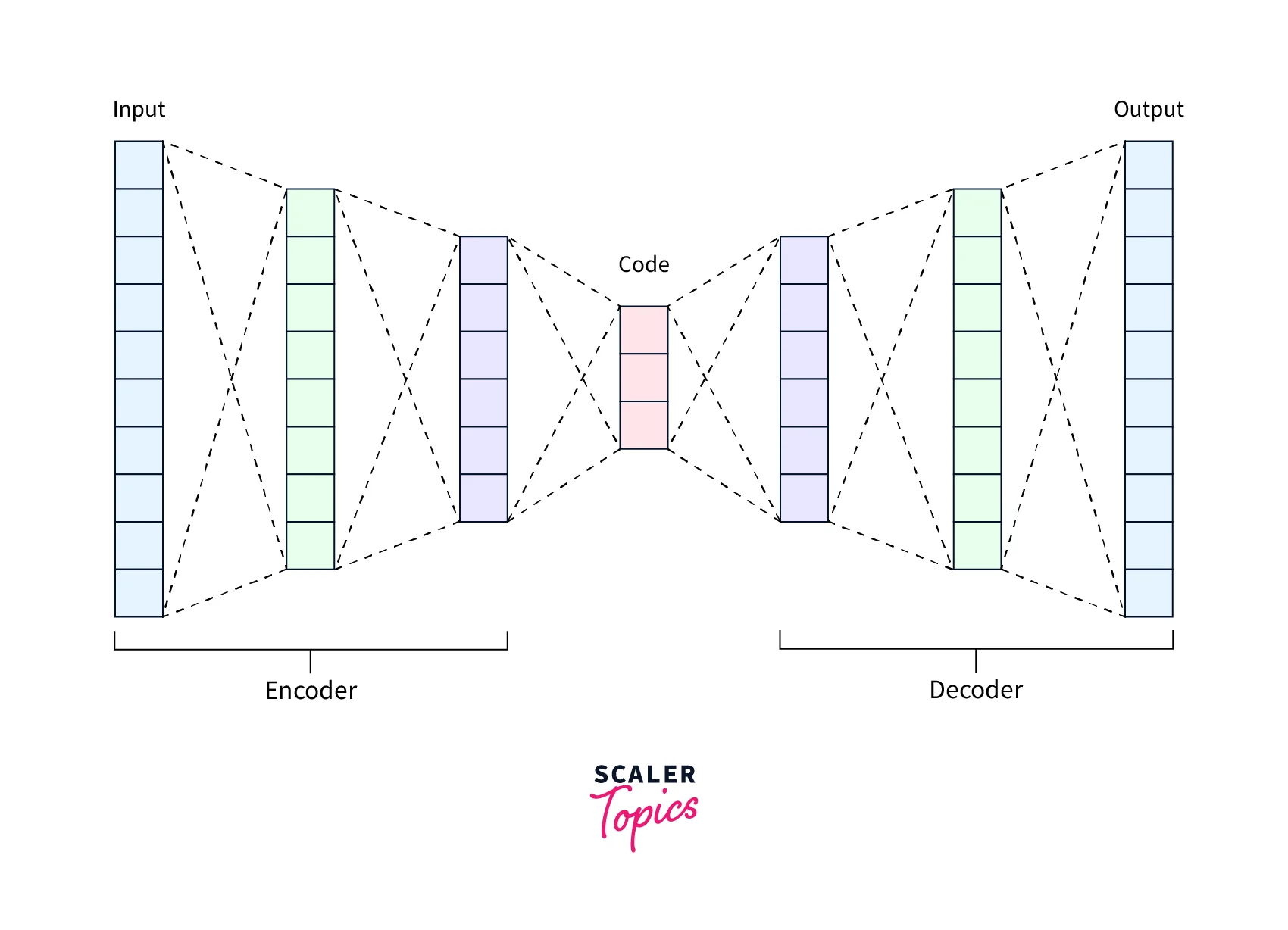
Autoencoders are neural networks that can be used for unsupervised dimensionality reduction. They consist of an encoder network that maps the high-dimensional data to a lower-dimensional latent space and a decoder network that reconstructs the data from the latent space. The encoder network learns a compressed representation of the data in the latent space by training the autoencoder to minimize the reconstruction error.

Backward Feature Elimination (BFE)

BFE is a feature selection technique that starts with all the features and removes them iteratively based on their impact on the model performance. It involves training a model on the full set of features, removing the feature with the least impact on the performance, retraining the model, and repeating the process until the desired number of features is obtained.

Forward Feature Selection (FFS)

FFS is a feature selection technique that starts with no features and adds them iteratively based on their impact on the model performance. It involves training a model on each feature individually and selecting the one that provides the most improvement in performance. The selected feature is then added to the feature set, and the process is repeated until the desired number of features is obtained.