Measuring Data Similarity and Dissimilarity in Data Mining

Introduction

Measuring similarity and dissimilarity in data mining is an important task that helps identify patterns and relationships in large datasets. To quantify the degree of similarity or dissimilarity between two data points or objects, mathematical functions called similarity and dissimilarity measures are used. Similarity measures produce a score that indicates the degree of similarity between two data points, while dissimilarity measures produce a score that indicates the degree of dissimilarity between two data points. These measures are crucial for many data mining tasks, such as identifying duplicate records, clustering, classification, and anomaly detection.

Let’s understand measures of similarity and dissimilarity in data mining and explore various methods to use these measures.

Basics of Similarity and Dissimilarity Measures

Similarity Measure

• A similarity measure is a mathematical function that quantifies the degree of similarity between two objects or data points. It is a numerical score measuring how alike two data points are.
• It takes two data points as input and produces a similarity score as output, typically ranging from 0 (completely dissimilar) to 1 (identical or perfectly similar).
• A similarity measure can be based on various mathematical techniques such as Cosine similarity, Jaccard similarity, and Pearson correlation coefficient.
• Similarity measures are generally used to identify duplicate records, equivalent instances, or identifying clusters.

Dissimilarity Measure

• A dissimilarity measure is a mathematical function that quantifies the degree of dissimilarity between two objects or data points. It is a numerical score measuring how different two data points are.
• It takes two data points as input and produces a dissimilarity score as output, ranging from 0 (identical or perfectly similar) to 1 (completely dissimilar). A few dissimilarity measures also have infinity as their upper limit.
• A dissimilarity measure can be obtained by using different techniques such as Euclidean distance, Manhattan distance, and Hamming distance.
• Dissimilarity measures are often used in identifying outliers, anomalies, or clusters.

Data Types Similarity and Dissimilarity Measures

• For nominal variables, these measures are binary, indicating whether two values are equal or not.
• For ordinal variables, it is the difference between two values that are normalized by the max distance. For the other variables, it is just a distance function.

Distinction Between Distance And Similarity

Distance is a typical measure of dissimilarity between two data points or objects, whereas similarity is a measure of how similar or alike two data points or objects are. Distance measures typically produce a non-negative value that increases as the data points become more dissimilar. Distance measures are fundamental principles for various algorithms, such as KNN, K-Means, etc. On the other hand, similarity measures typically produce a non-negative value that increases as the data points become more similar.

Similarity Measures

• Similarity measures are mathematical functions used to determine the degree of similarity between two data points or objects. These measures produce a score that indicates how similar or alike the two data points are.
• It takes two data points as input and produces a similarity score as output, typically ranging from 0 (completely dissimilar) to 1 (identical or perfectly similar).
• Similarity measures also have some well-known properties -
  • $sim(A, B) = 1$ (or maximum similarity) only if $A = B$
  • Typical range - $(0 ≤ sim ≤ 1)$
  • Symmetry - $sim(A, B) = sim(B, A)$ for all $A$ and $B$

Now let’s explore a few of the most commonly used similarity measures in data mining.

Cosine Similarity

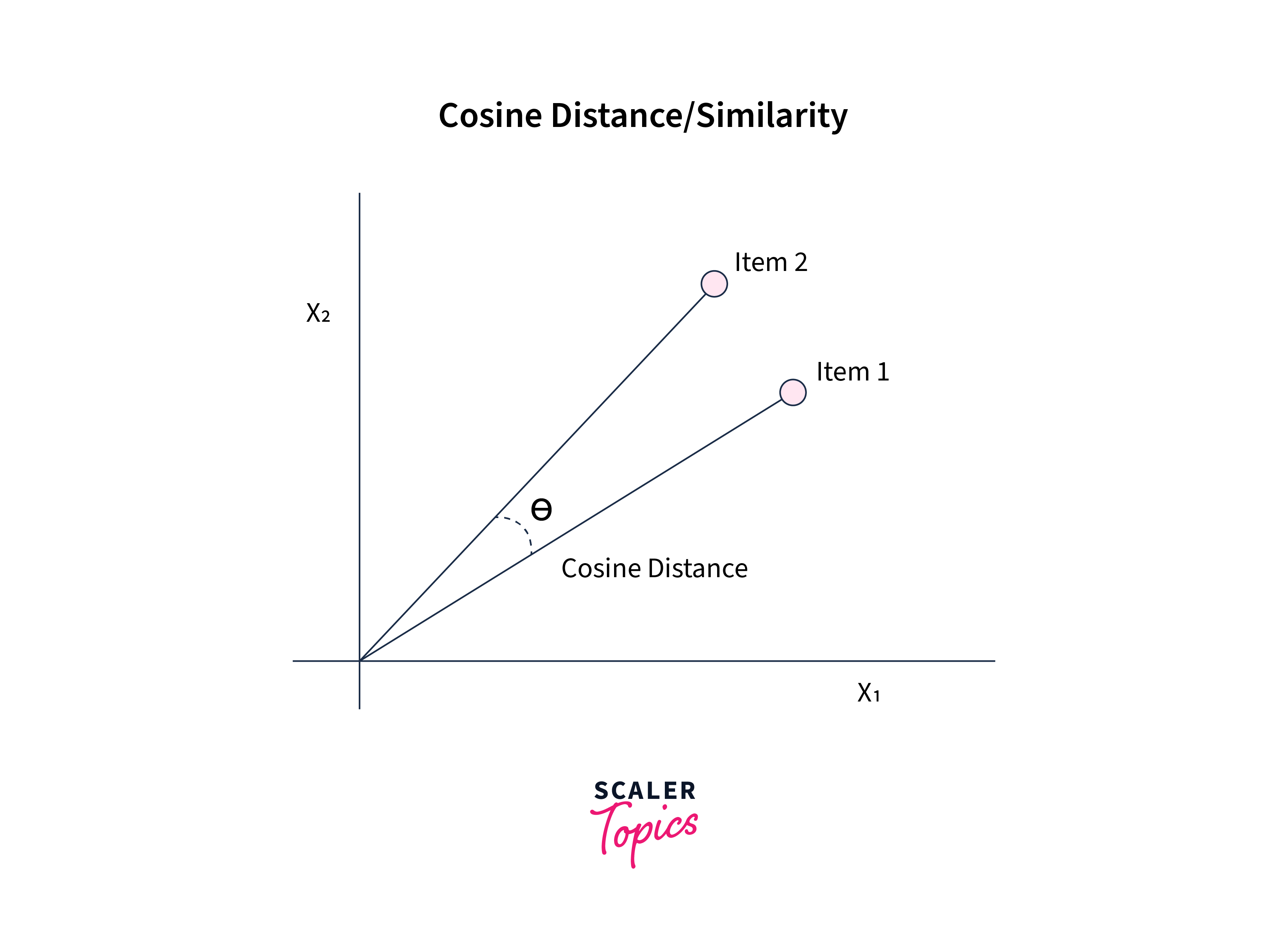
Cosine similarity is a widely used similarity measure in data mining and information retrieval. It measures the cosine of the angle between two non-zero vectors in a multi-dimensional space. In the context of data mining, these vectors represent the feature vectors of two data points. The cosine similarity score ranges from 0 to 1, with 0 indicating no similarity and 1 indicating perfect similarity.

The cosine similarity between two vectors is calculated as the dot product of the vectors divided by the product of their magnitudes. This calculation can be represented mathematically as follows -

where A and B are the feature vectors of two data points, "." denotes the dot product, and "||" denotes the magnitude of the vector.

Jaccard Similarity

The Jaccard similarity is another widely used similarity measure in data mining, particularly in text analysis and clustering. It measures the similarity between two sets of data by calculating the ratio of the intersection of the sets to their union. The Jaccard similarity score ranges from 0 to 1, with 0 indicating no similarity and 1 indicating perfect similarity.

The Jaccard similarity between two sets A and B is calculated as follows -

where $|\mathbf{A} ∩ \mathbf{B}|$ is the size of the intersection of sets $\mathbf{A}$ and $\mathbf{B}$, and $|\mathbf{A} ∪ \mathbf{B}|$ is the size of the union of sets $\mathbf{A}$ and $\mathbf{B}$.

Pearson Correlation Coefficient

The Pearson correlation coefficient is a widely used similarity measure in data mining and statistical analysis. It measures the linear correlation between two continuous variables, X and Y. The Pearson correlation coefficient ranges from -1 to +1, with -1 indicating a perfect negative correlation, 0 indicating no correlation, and +1 indicating a perfect positive correlation. The Pearson correlation coefficient is commonly used in data mining applications such as feature selection and regression analysis. It can help identify variables that are highly correlated with each other, which can be useful for reducing the dimensionality of a dataset. In regression analysis, it can also be used to predict the value of one variable based on the value of another variable.

The Pearson correlation coefficient between two variables, X and Y, is calculated as follows -

where $\operatorname{cov}(X,Y)$ is the covariance between variables $X$ and $Y$, and $\sigma_X$ and $\sigma_Y$ are the standard deviations of variables $X$ and $Y$, respectively.

Sørensen-Dice Coefficient

The Sørensen-Dice coefficient, also known as the Dice similarity index or Dice coefficient, is a similarity measure used to compare the similarity between two sets of data, typically used in the context of text or image analysis. The coefficient ranges from 0 to 1, with 0 indicating no similarity and 1 indicating perfect similarity. The Sørensen-Dice coefficient is commonly used in text analysis to compare the similarity between two documents based on the set of words or terms they contain. It is also used in image analysis to compare the similarity between two images based on the set of pixels they contain.

The Sørensen-Dice coefficient between two sets, A and B, is calculated as follows -

where $|A ∩ B|$ is the size of the intersection of sets $A$ and $B$, and $|A|$ and $|B|$ are the sizes of sets $A$ and $B$, respectively.

Choosing The Appropriate Similarity Measure

Choosing an appropriate similarity measure depends on the nature of the data and the specific task at hand. Here are some factors to consider when choosing a similarity measure -

• Different similarity measures are suitable for different data types, such as continuous or categorical data, text or image data, etc. For example, the Pearson correlation coefficient, which is only suitable for continuous variables.
• Some similarity measures are sensitive to the scale of measurement of the data.
• The choice of similarity measure also depends on the specific task at hand. For example, cosine similarity is often used in information retrieval and text mining, while Jaccard similarity is commonly used in clustering and recommendation systems.
• Some similarity measures are more robust to noise and outliers in the data than others. For example, the Sørensen-Dice coefficient is less sensitive to noise.

Dissimilarity Measures

• Dissimilarity measures are used to quantify the degree of difference or distance between two objects or data points.
• Dissimilarity measures can be considered the inverse of similarity measures, where the similarity measure returns a high value for similar objects and a low value for dissimilar objects, and the dissimilarity measure returns a low value for similar objects and a high value for dissimilar objects.
• Dissimilarity measures also have some well-known properties -
  • Positivity - $dissim(A, B) ≥ 0$ for all $A$ and $B$, and $dissim(A, B) = 0$ only if $A = B$.
  • Symmetry - $dissim(A, B) = dissim(B, A)$ for all $A$ and $B$
  • Triangle Inequality - $dissim(A, C) ≤ dissim(A, B) + d(B, C)$ for all points $A$, $B$, and $C$.

Let’s explore a few of the commonly used dissimilarity or distance measures in data mining.

Euclidean Distance

Euclidean distance is a commonly used dissimilarity measure that quantifies the distance between two points in a multidimensional space. It is named after the ancient Greek mathematician Euclid, who first studied its properties. The Euclidean distance between two points $X$ and $Y$ in an n-dimensional space is defined as the square root of the sum of the squared differences between their corresponding coordinates, as shown below -

Euclidean distance is commonly used in clustering, classification, and anomaly detection applications in data mining and machine learning. It has the advantage of being easy to interpret and visualize. However, it can be sensitive to the scale of the data and may not perform well when dealing with high-dimensional data or data with outliers.

Manhattan Distance

Manhattan distance, also known as city block distance, is a dissimilarity measure that quantifies the distance between two points in a multidimensional space. It is named after the geometric structure of the streets in Manhattan, where the distance between two points is measured by the number of blocks one has to walk horizontally and vertically to reach the other point. The Manhattan distance between two points $x$ and $y$ in an n-dimensional space is defined as the sum of the absolute differences between their corresponding coordinates, as shown below -

In data mining and machine learning, the Manhattan distance is commonly used in clustering, classification, and anomaly detection applications. It is particularly useful when dealing with high-dimensional data, sparse data, or data with outliers, as it is less sensitive to extreme values than the Euclidean distance. However, it may not be suitable for data that exhibit complex geometric structures or nonlinear relationships between features.

Minkowski Distance

Minkowski distance is a generalization of Euclidean distance and Manhattan distance, which are special cases of Minkowski distance. The Minkowski distance between two points $x$ and $y$ in an n-dimensional space can be defined as -

Where $p$ is a parameter that determines the degree of the Minkowski distance. When $p = 1$, the Minkowski distance reduces to the Manhattan distance, and when $p = 2$, it reduces to the Euclidean distance. When $p > 2$, it is sometimes referred to as a "higher-order" distance metric.

Hamming Distance

Hamming distance is a distance metric used to measure the dissimilarity between two strings of equal length. It is defined as the number of positions at which the corresponding symbols in the two strings are different.

For example, consider the strings "101010" and "111000". The Hamming distance between these two strings is three since there are three positions at which the corresponding symbols are different: the second, fourth, and sixth positions.

Hamming distance is often used in error-correcting codes and cryptography, where it is important to detect and correct errors in data transmission. It is also used in data mining and machine learning applications to compare categorical or binary data, such as DNA sequences or binary feature vectors.

Choosing The Appropriate Dissimilarity Measure

Similar to similarity measures, choosing the appropriate dissimilarity measure also depends on the nature of the data and the specific task at hand. Here are some factors to consider when selecting a dissimilarity measure -

• Different dissimilarity measures are appropriate for different types of data. For example, Hamming distance is suitable for binary or string data, while Euclidean distance is appropriate for continuous numerical data.
• The scale of the data can also affect the choice of dissimilarity measure. For instance, if the range of a feature is much larger than the range of another feature, Euclidean distance may not be the best measure to use. In this case, normalization or standardization of the data may be required, or a different measure, such as Manhattan distance, could be used.
• The number of features or dimensions in the data can also impact the choice of dissimilarity measure. For high-dimensional data, a more robust measure such as Mahalanobis distance may be more appropriate.

Advanced Techniques and Recent Developments

• Measures for similarity and dissimilarity in data mining can be learned from labeled data in a supervised learning setting. One common approach to learning supervised similarity and dissimilarity measures is to train a binary classifier that distinguishes between similar and dissimilar pairs of examples. Another approach is to train a regression model that predicts the degree of similarity or dissimilarity between pairs of examples.
• Similarly, ensemble techniques are used for measures of similarity and dissimilarity in data mining when no single measure performs well on its own or when multiple measures capture different aspects of the data. Ensemble techniques for similarity and dissimilarity measures involve combining multiple measures into a single measure to improve the overall performance. For example, in a k-NN classifier, each neighbor can be classified using a different similarity measure. The final classification decision can then be made by combining the decisions of all neighbors using an ensemble technique.
• Recently, deep learning is also being used to learn measures of similarity and dissimilarity in data mining. It involves using neural networks to learn the similarity or dissimilarity between pairs of examples. One common approach to deep learning for similarity and dissimilarity measures is to use Siamese networks. Siamese networks consist of two identical neural networks that share weights. Each network takes as input one of the two examples to be compared and produces a feature vector that represents the example. The two feature vectors are then compared using a distance or similarity measure, such as Euclidean distance or cosine similarity, to produce a final output.