Clustering Methods - Partitioning in Data Mining
Overview
Partitioning methods in data mining is a popular family of clustering algorithms that partition a dataset into K distinct clusters. These algorithms aim to group similar data points together while maximizing the differences between the clusters. The most widely used partitioning method is the K-means algorithm, which randomly assigns data points to clusters and iteratively refines the clusters' centroids until convergence. Other popular partitioning methods in data mining include K-medoids, Fuzzy C-means, and Hierarchical K-means. The choice of the algorithm depends on the specific clustering problem and the dataset characteristics.
Introduction to Partitioning Methods
Partitioning methods are a widely used family of clustering algorithms in data mining that aim to partition a dataset into K clusters. These algorithms attempt to group similar data points together while maximizing the differences between the clusters. Partitioning methods work by iteratively refining the cluster centroids until convergence is reached. These algorithms are popular for their speed and scalability in handling large datasets.
The most widely used partitioning method is the K-means algorithm. Other popular partitioning methods include K-medoids, Fuzzy C-means, and Hierarchical K-means. The K-medoids are similar to K-means but use medoids instead of centroids as cluster representatives. Fuzzy C-means is a soft clustering algorithm that allows data points to belong to multiple clusters with varying degrees of membership.
Partitioning methods offer several benefits, including speed, scalability, and simplicity. They are relatively easy to implement and can handle large datasets. Partitioning methods are also effective in identifying natural clusters within data and can be used for various applications, such as customer segmentation, image segmentation, and anomaly detection.
K-Means (A Centroid-Based Technique)
K-means is the most popular algorithm in partitioning methods for clustering. It partitions a dataset into K clusters, where K is a user-defined parameter. Let’s understand the K-Means algorithm in more detail.
How does K-Means Work?
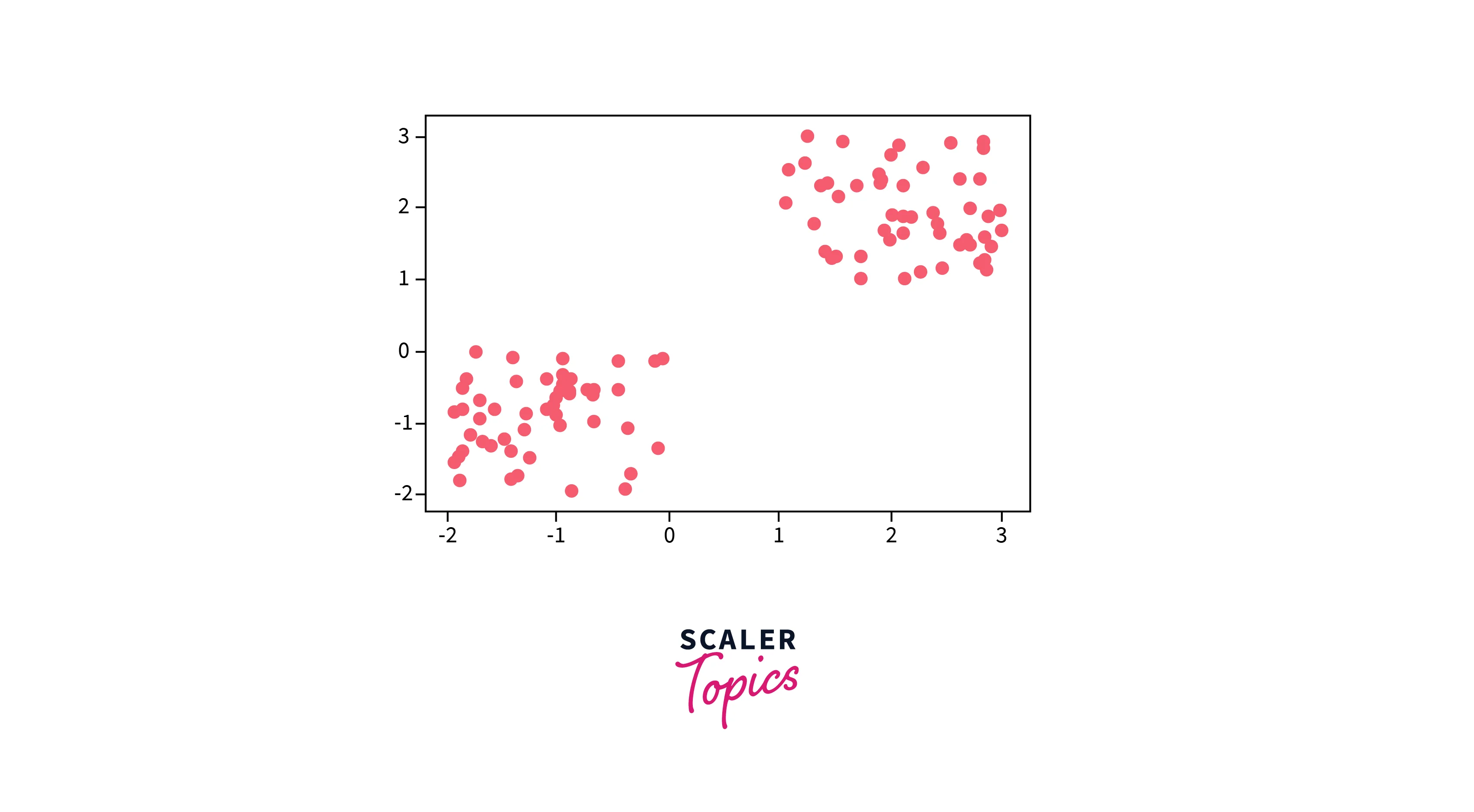
The K-Means algorithm begins by randomly assigning each data point to a cluster. It then iteratively refines the clusters' centroids until convergence. The refinement process involves calculating the mean of the data points assigned to each cluster and updating the cluster centroids' coordinates accordingly. The algorithm continues to iterate until convergence, meaning the cluster assignments no longer change. K-means clustering aims to minimize the sum of squared distances between each data point and its assigned cluster centroid. K-means is widely used in various applications, such as customer segmentation, image segmentation, and anomaly detection, due to its simplicity and efficiency in handling large datasets. For example, the K-Means algorithm can group data points into two clusters, as shown below.
Algorithm
Here is a high-level overview of the algorithm to implement K-means clustering:
- Initialize K cluster centroids randomly.
- Assign each data point to the nearest centroid.
- Recalculate the centroids' coordinates by computing the mean of the data points assigned to each cluster.
- Repeat steps 2 and 3 until the cluster assignments no longer change or a maximum number of iterations is reached.
- Return the K clusters and their respective centroids.
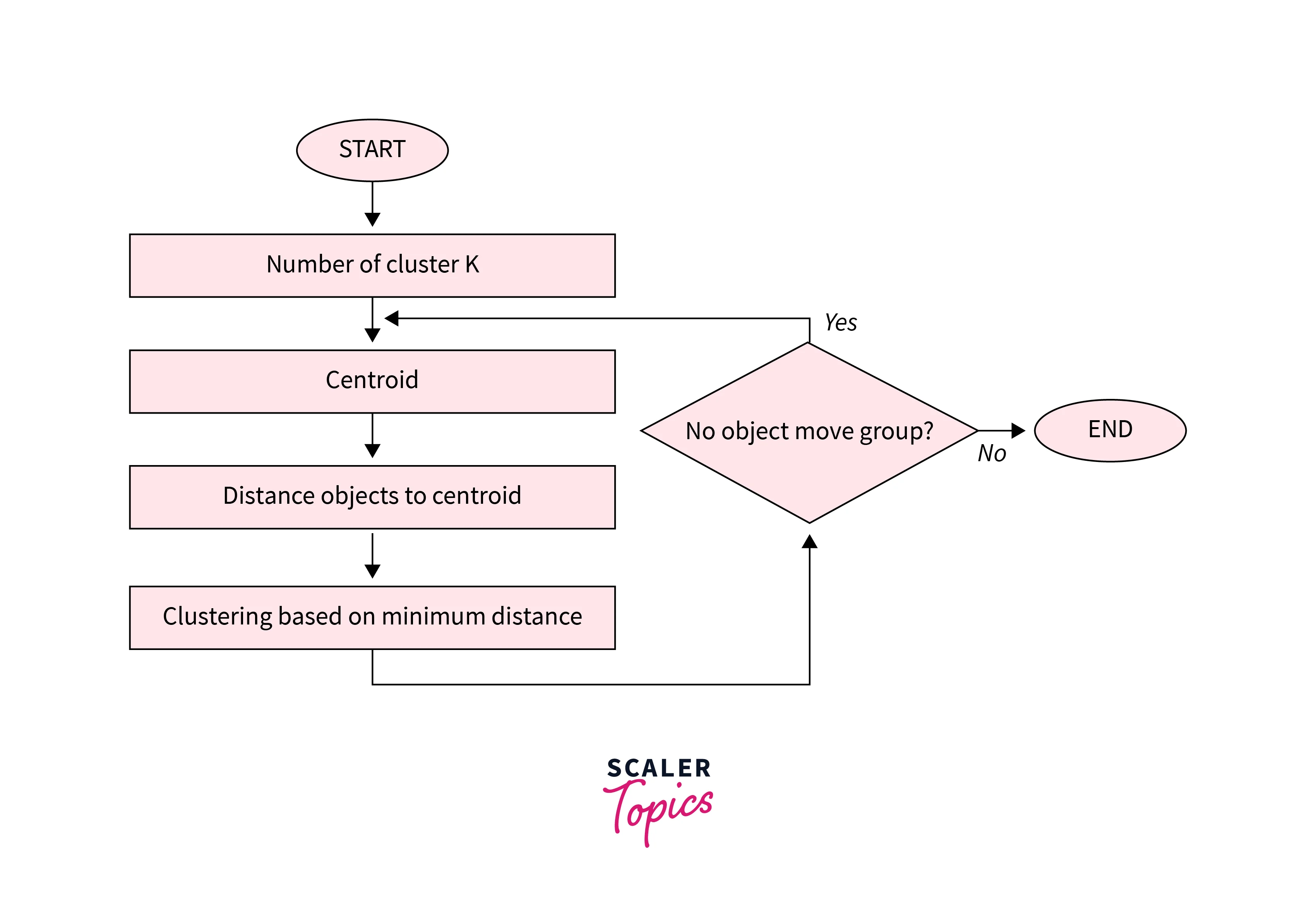
The flow chart of the K-Means algorithm is shown in the figure below.
Advantages of K-Means
Here are some advantages of the K-means clustering algorithm -
- Scalability - K-means is a scalable algorithm that can handle large datasets with high dimensionality. This is because it only requires calculating the distances between data points and their assigned cluster centroids.
- Speed - K-means is a relatively fast algorithm, making it suitable for real-time or near-real-time applications. It can handle datasets with millions of data points and converge to a solution in a few iterations.
- Simplicity - K-means is a simple algorithm to implement and understand. It only requires specifying the number of clusters and the initial centroids, and it iteratively refines the clusters' centroids until convergence.
- Interpretability - K-means provide interpretable results, as the clusters' centroids represent the centre points of the clusters. This makes it easy to interpret and understand the clustering results.
Disadvantages of K-Means
Here are some disadvantages of the K-means clustering algorithm -
- Curse of dimensionality - K-means is prone to the curse of dimensionality, which refers to the problem of high-dimensional data spaces. In high-dimensional spaces, the distance between any two data points becomes almost the same, making it difficult to differentiate between clusters.
- User-defined K - K-means requires the user to specify the number of clusters (K) beforehand. This can be challenging if the user does not have prior knowledge of the data or if the optimal number of clusters is unknown.
- Non-convex shape clusters - K-means assumes that the clusters are spherical, which means it cannot handle datasets with non-convex shape clusters. In such cases, other clustering algorithms, such as hierarchical clustering or DBSCAN, may be more suitable.
- Unable to handle noisy data - K-means are sensitive to noisy data or outliers, which can significantly affect the clustering results. Preprocessing techniques, such as outlier detection or noise reduction, may be required to address this issue.
For a Hands-On Approach, Check out Scaler's Data Scientist Course that Offers Interactive Modules. Enroll and Get Certified by the Best!
What are K-medoids?
K-medoids is a clustering algorithm that is similar to K-means but uses medoids instead of centroids. Medoids are representative data points within a cluster that are most centrally located concerning all other data points in the cluster. In contrast, centroids are the arithmetic mean of all the data points in a cluster.
In the K-medoids algorithm, the initial medoids are randomly selected from the dataset, and the algorithm iteratively updates the medoids until convergence. The algorithm assigns each data point to the nearest medoid and then computes the total dissimilarity between each medoid and its assigned data points. It then selects the data point with the lowest dissimilarity as the new medoid for each cluster.
Difference Between K-Means & K-Medoids Clustering
Here is a comparison between K-Means and K-Medoids clustering algorithms in a tabular format.
| Factor | K-Means | K-Medoids |
| Objective | Minimizing the sum of squared distances between data points and their assigned cluster centroids. | Minimizing the sum of dissimilarities between data points and their assigned cluster medoids. |
| Cluster Center Metric | Use centroids, which are the arithmetic means of all data points in a cluster. | Use medoids, which are representative data points within each cluster that are most centrally located concerning all other data points in the cluster. |
| Robustness | Less robust to noise and outliers. | More robust to noise and outliers. |
| Computational Complexity | Faster and more efficient for large datasets. | Slower and less efficient for large datasets. |
| Cluster Shape | Assumes spherical clusters and is not suitable for non-convex clusters. | Can handle non-convex clusters. |
| Initialization | Requires initial centroids to be randomly selected. | Requires initial medoids to be randomly selected. |
| Applications | Suitable for applications such as customer segmentation, image segmentation, and anomaly detection. | Suitable for applications where robustness to noise and outliers is important, such as clustering DNA sequences or gene expression data. |
Which is More Robust - K-Means or K-Medoids?
The K-Medoids algorithm is generally considered more robust than the K-Means algorithm, particularly when dealing with noisy and outlier-prone datasets. This is because the K-Medoids algorithm uses medoids as cluster representatives instead of centroids, which are more robust to outliers and noise.
In K-Means, the centroid of a cluster is the mean of all the data points in that cluster. This means that any outlier or noise point in the cluster can significantly influence the location of the centroid. On the other hand, the K-Medoids algorithm chooses a representative data point within the cluster, which is less affected by noise and outliers than the centroid. This makes the K-Medoids algorithm a better choice for datasets with a high degree of noise and outliers.
Applications of Clustering
Here are a few of the most common applications of clustering -
- Customer Segmentation - Clustering is often used in marketing to group customers with similar needs and preferences together. By clustering customers based on their purchase history, demographic information, and behaviour patterns, companies can tailor their marketing strategies to meet the needs of different customer groups better.
- Image Segmentation - Clustering is widely used in computer vision to segment images into different regions based on their visual characteristics. This can be used for various applications such as object recognition, face detection, and medical image analysis.
- Anomaly Detection - Clustering can identify unusual patterns or outliers in data that do not conform to expected behaviour. This is useful in various domains, such as fraud detection, network intrusion detection, and equipment failure prediction.
- Document Clustering - Clustering is used in natural language processing to group similar documents together based on their content. This can be used for various applications, such as topic modelling, sentiment analysis, and text classification.
- Gene Expression Analysis - Clustering is widely used in bioinformatics to group genes with similar expression patterns together. This can help researchers identify co-regulated genes and gain insights into the underlying biological processes involved in gene expression.
Conclusion
- Partitioning methods in data mining are one of the most popular types of clustering algorithms and involve dividing the data into a fixed number of clusters or partitions.
- K-Means is the most widely used partitioning algorithm and works by iteratively updating the centroids of the clusters to minimize the sum of squared distances between the data points and their assigned centroid.
- K-Medoids is a variant of K-Means that uses medoids as the cluster representatives instead of centroids and is more robust to noise and outliers.
- K-Means and K-Medoids both have their strengths and weaknesses, and the choice of algorithm depends on the specific characteristics of the dataset and the goals of the analysis.
