Decimal to Octal in Python
FREE
Overview
The decimal system is the most widely used number system. While computers only understand binary and binary, octal and hexadecimal number systems are closely related, so we may require to convert decimal into these systems.
Transform Your Career
Choose from our industry-leading programs designed for career success
Modern Software and AI Engineering Program
Master full-stack development with AI integration
+1000 moreModern Data Science and ML with specialisation in AI
Advanced data science techniques with AI specialization
+1000 moreAdvanced AIML with Specialisation in Agentic AI
Deep dive into AIML with focus on Agentic systems
+1000 moreDevOps, Cloud & AI Platform Engineering
Build and manage AI-powered cloud infrastructure
+1000 moreAI Engineering Advanced Certification by IIT-Roorkee
Premier AI engineering certification from IIT-Roorkee
Introduction
Suppose we are given a decimal number as input, and we need to write an algorithm to convert the given decimal number into its octal number system representation, i.e. convert the number with base value 10 to base value 8. The base value of a number system determines the number of digits used to represent a numeric value.
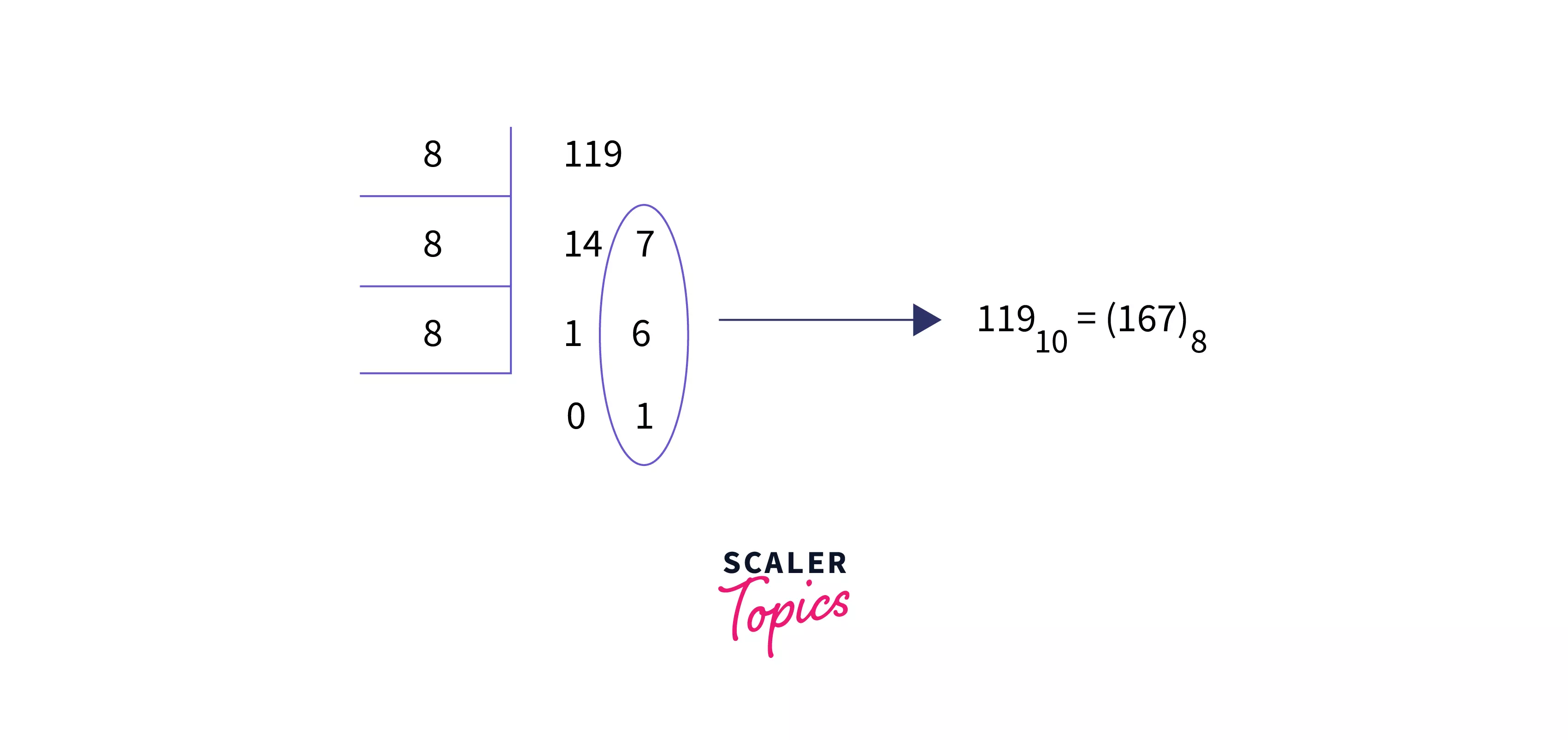
The binary number system uses two digits 0 and 1, the octal number system uses 8 digits from 0-7, and the decimal number system uses ten digits 0-9 to represent any numeric value.
A number with the prefix 0b is considered binary, 0o is considered octal, and 0x is hexadecimal.
For Example- 60 = 0b100000 = 0o40 = 0x20
Algorithm
- Store the remainder when the number is divided by 8 in an array.
- Divide the number by 8 now
- Repeat the above two steps until the number is not equal to 0.
- Print the array in reverse order now.
For Example:
If the given decimal number is 10,
Step 1: When 10 is divided by 8, the remainder is 2. Therefore, arr[0] = 2.
Step 2: Divide 10 by 8. New number is 10/8 = 1.
Step 3: When 1 is divided by 8, the remainder is 1. Therefore, arr[1] = 1.
Step 4: Divide 1 by 8. New number is 1/8 = 0.
Step 5: Since the number becomes = 0, we can stop repeating steps and print the array in reverse order.
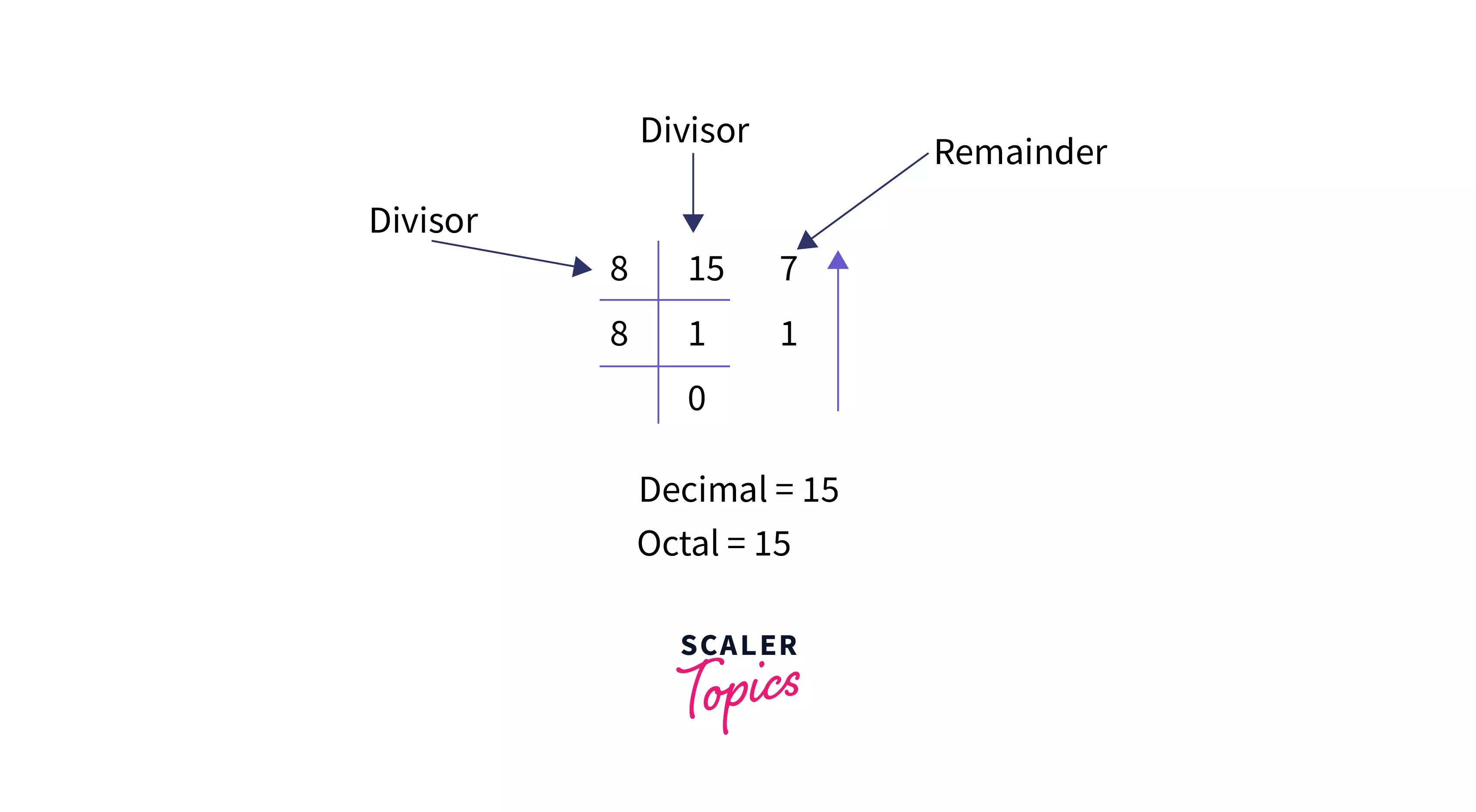
Therefore, the equivalent octal number is '12'.
Decimal to Octal in Python Using Loop
The common method of calculating the octal representation of a decimal number is to divide the number by 8 until it becomes 0. After the division is over, we print the array storing the remainders at each division point in reverse order.
Calling the Function
DecimalToOctal(33)
Output:
The number of iterations in the above program is equal to the number of bits in the octal representation of the given number n, which makes the Time Complexity: O(log N)
We initialize an array at the starting of the program to store the remainders and make the Space Complexity: O(N)
Decimal to Octal in Python Using Recursion
When we want to convert a decimal number n into octal using recursion, we have to pass the quotient (n/8) to the next recursive call and output the remainder value (n%8).
We repeat the process until the number reduces to zero. Since recursion implements stack, the remainders will get printed in a bottom-up manner, and we get the equivalent octal number.
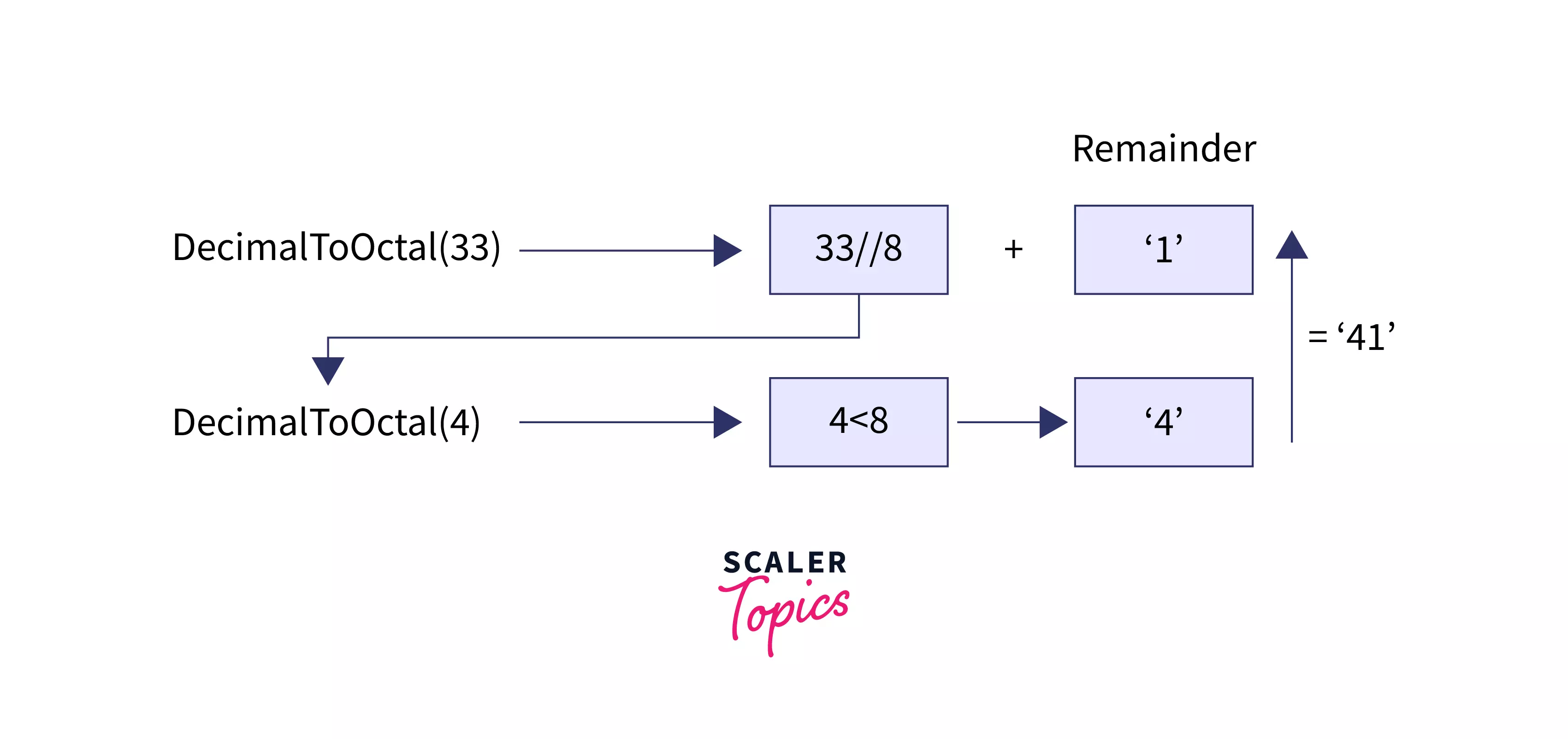
Output:
Scaler Placement Report and Statistics
Scaler learners achieved 2.5x salary growth with average post-Scaler CTC reaching ₹23L.
Google
Amazon
Microsoft
Flipkart
Adobe1200+ moreDecimal to Octal in Python Using O(1) Space Complexity
This method of converting a decimal number to its octal representation divides the decimal by 8 until it reduces to 0. After the division is over, if we stack the remainders in a bottom-up manner, the result value will be the equivalent octal number.
Output
Time Complexity: O(log N)
No extra array is created for storing the remainders. That's why the Space Complexity: O(1)
In the above program, we have initialized the octal number as octal to 0, count to 1, and the decimal variable as deci to n. After this step, we calculate the remainder when the decimal number is divided by 8, the value of octal is updated by octalNum + (remainder * count), the value of count is increased by count*10, and at last the decimal number deci is divided by 8. The whole process runs until the decimal variable becomes zero.
Decimal to Octal in Python Using oct()
The built-in Python method oct() returns the equivalent octal representation of the decimal number passed as a parameter. The oct() function returns an octal number in the form of 0oxyz, where xyz is the actual octal value.
Syntax
The syntax of oct() is
Turn Learning into Career Growth
Parameters
The oct() function takes a single parameter. This parameter could be an integer number (binary, decimal, or hexadecimal).
Return Values
The oct() function returns an octal string from the given integer number.
Working of oct() in Python
Output
The above oct(15) returns 0o17 as the output, which means the actual octal value for decimal number 15 is 17.
Conclusion
- The base value of a number system determines the number of digits used to represent a numeric value.
- The binary number system uses two digits, 0 and 1, the octal number system uses 8 digits from 0-7 and the decimal number system uses 10 digits 0-9 to represent any numeric value.
- Python has a built-in oct() function that returns the equivalent octal representation of the decimal number passed as a parameter.