Data Encryption Standard (DES) Algorithm
Introduction to DES Algorithm
The arrival of the information age marked an abundance of data being produced. For the necessity of people’s privacy, protecting vital and sensitive information has been of great urgency, therefore the way information is protected during its transmission over networks and storage in system memory is given way more importance.
With the arrival of scientific discipline technologies during the 1970’s, IBM came out with the DES(Data Encryption Standard, DES) algorithm, a symmetric-key algorithm based on an algorithm given earlier by Horst Feistel. Symmetric key algorithms are those where the encryption and decryption of message and ciphertext is done using the same key. The algorithm was submitted to the National Bureau of Standards, USA.
In 1976, after consultation with the National Security Agency (NSA), the DES algorithm was given a few modifications and was selected, and published as an official Federal Information Processing Standard (FIPS) in America in 1977.
What is DES Algorithm?
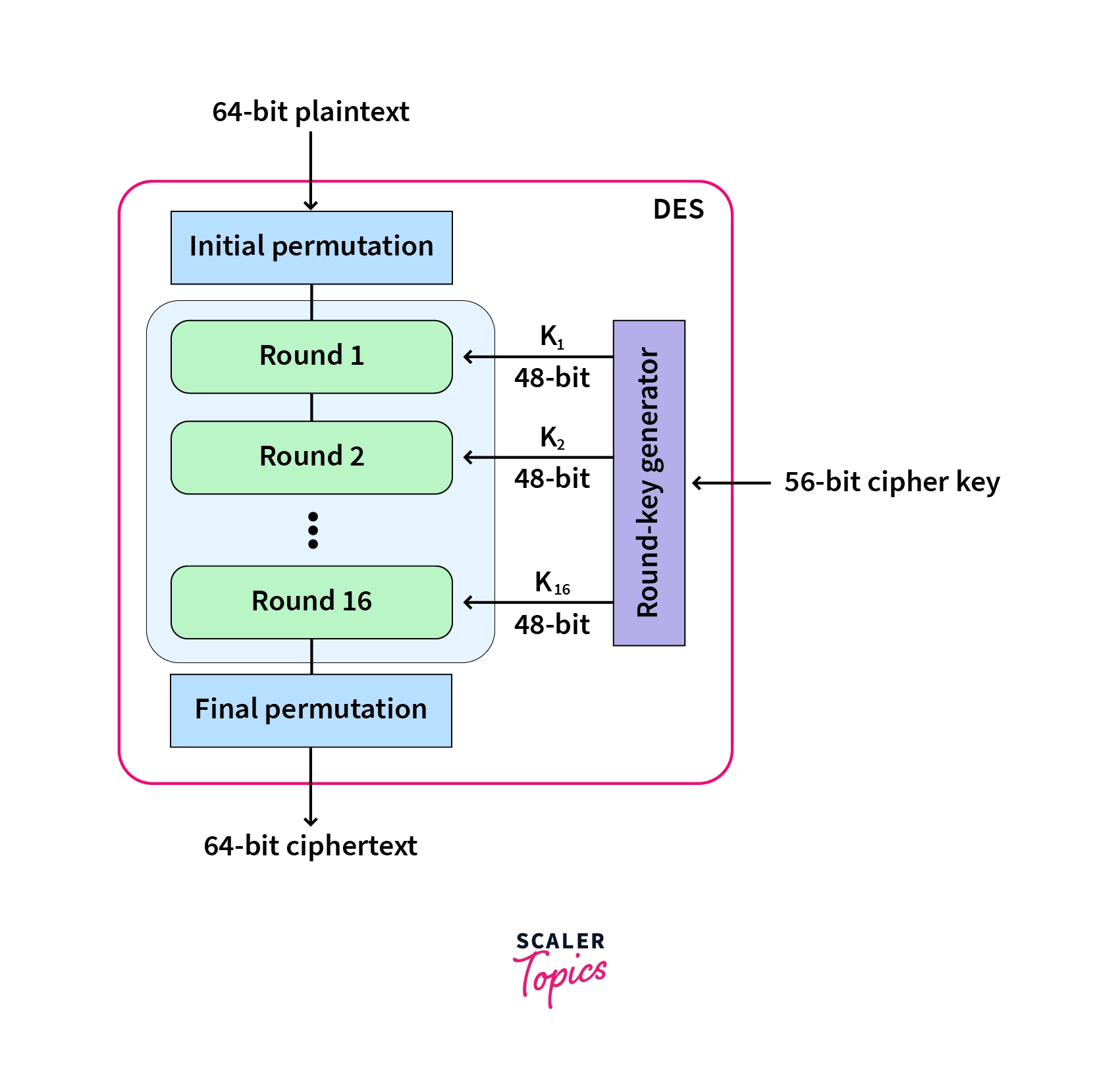
The Data Encryption Standard algorithm is a block cipher algorithm that takes in 64-bit blocks of plaintext at a time as input and produces 64-bit blocks of cipher text at a time, using a 48-bit key for each input. In block cipher algorithms, the text to be encrypted is broken into ‘blocks’ of text, and each block is encrypted separately using the key.

The decryption process is the exact opposite of the encryption. It takes in a 64 bit block of ciphertext, and produces the 64 bit block of plaintext using the same 48 bit key during encryption.
The encryptor and the decryptor need to use the same key, otherwise, they will not be able to communicate together.
The DES algorithm was successful in the early days of the internet, but its short key length of 56 bits makes it too insecure for today’s applications. With the evolution of technology and the increase in computing power, an attacker with sufficient computing resources can break the key within a few minutes. It has however been highly influential in the development and advancement of cryptography.
Steps for Key Generation
Computers don’t deal with letters or numbers. All the plaintext characters are converted to binary before they’re encrypted. During the encryption process, data is separated into blocks for processing. The DES algorithm makes a 64 bit block size, hence breaking the binary plaintext into blocks of 64 bits each.
When the last block is not the required 64 bits long, it is padded before anything is done. Padding makes sure that extra information to the block is added in order to get it to a length of 64 bits. Padding can also ensure that the encrypted data is harder to crack.
Keys are used to change the end result of an encryption process in such a way that it wouldn’t be possible for an attacker to predict the plaintext just by knowing the algorithm.
DES begins with one key, which is used to form sub keys that are applied during each ‘round’. To produce the final ciphertext, the DES algorithm is run 16 times, and each time it is run is called a round with the output of one round acting as the input for the next. This lets the plaintext be confused as much as possible.
Now, the first thing we do is choose a random 64 bit number to be our key K. Mind you, both the sender and the receiver need to have the same 64 bit key to communicate.
For each round, one subkey is needed. This subkey is unique to that round, and is essentially a permutation of our master key K that we set at the beginning. A total of 16 subkeys are generated, one for each round. They’re denoted as to .
- The first step to derive our round keys is to permute the key according to the Permuted Choice-1 (PC-1) table. We shall rearrange the elements of our data block using the following PC1 table.

The “C” and “D” are the "Left" and "Right" halves of the data block. The numbers given in the table decide which bits from the input key belong to which (left or right) sections of the state of the key scheduling.
During the PC-1 permutation, each bit of the original key is rearranged and placed at a new position in accordance with the table. Since the first cell of table "C" reads 57, the 57th bit from the original key will be placed in the first cell. The second cell reads 49, hence the second bit of our new key will be the 49th bit from the old block. Similarly, all the other numbers from the old block are arranged in the order of table “C” to make our new key. Once the block is arranged in order of table”C”, we jump to table “D” to complete the second half of our new key.
Looking at the table and the key, you may have noticed that they are only 56 bits in length, rather than 64 bits. This is because every eighth bit (8, 16, 24, 32, 40, 48, 56) is specified for use as parity bits to ensure that the key has been received correctly. Due to these parity bits, the DES algorithm has the security of a 56 bit key in practice.
Our 56 bit key is now split into left and right halves, each 28 bits in length. We will now be using this for our next step.
- The next step is shifting the key to the left either by 1 or 2 bits depending on the round number. The exact number to shift is given in the following table:
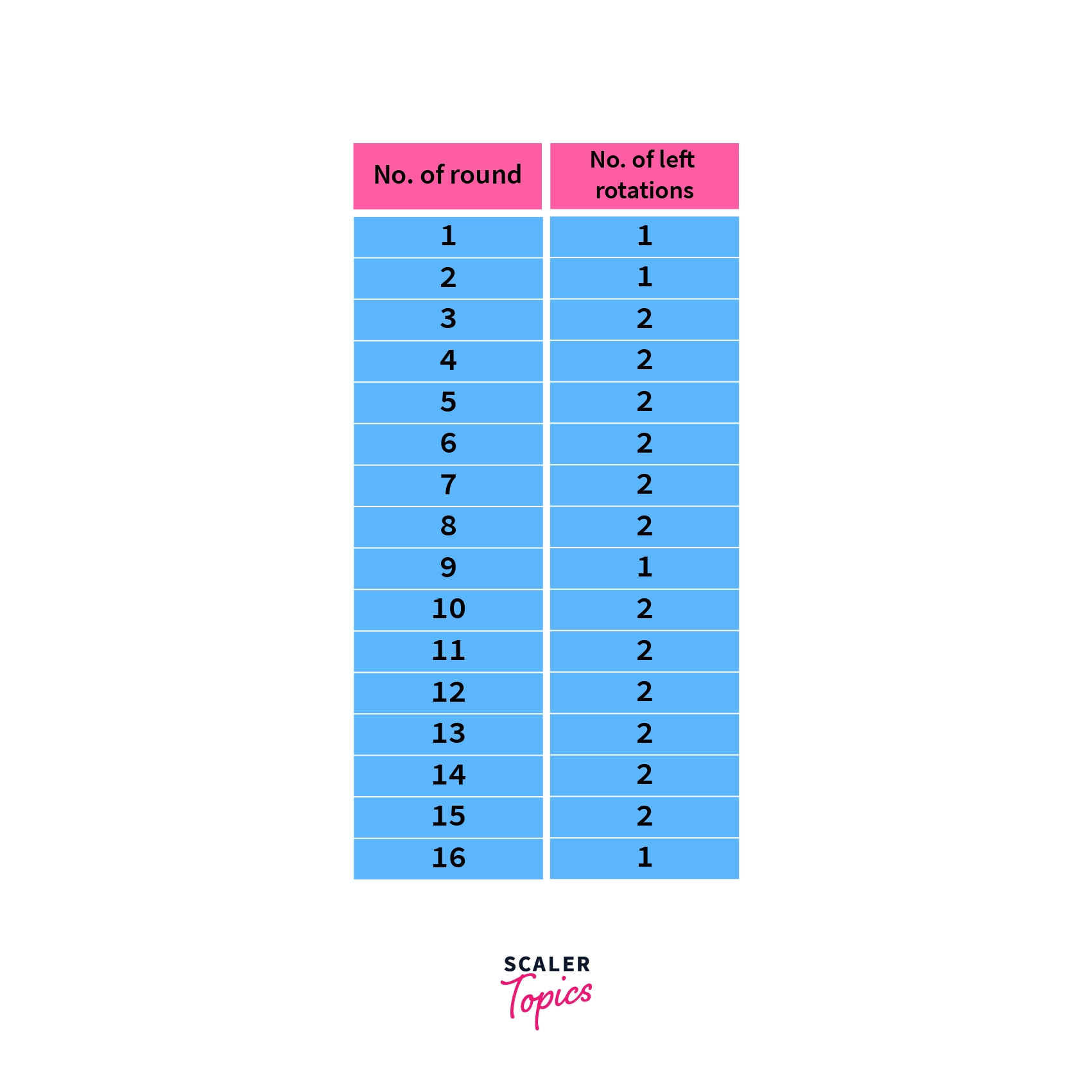
In these rounds, the numbers are shifted to the left by the distances given in the table, with each of the shifts being applied to the result of the previous round.
For example, if we’re in the 5th encryption round and had 1101101101101101 as our key, then according to the table we’ll have to left shift it by 2 spaces. Hence after this round, our key will now be: 0110110110110111.
Hence, sixteen different subkeys are generated, with one for each round of the DES process.
- Next, we permute the key according to the Permuted Choice-2 table as given. Here we once again rearrange the bits in our key according to the table below.
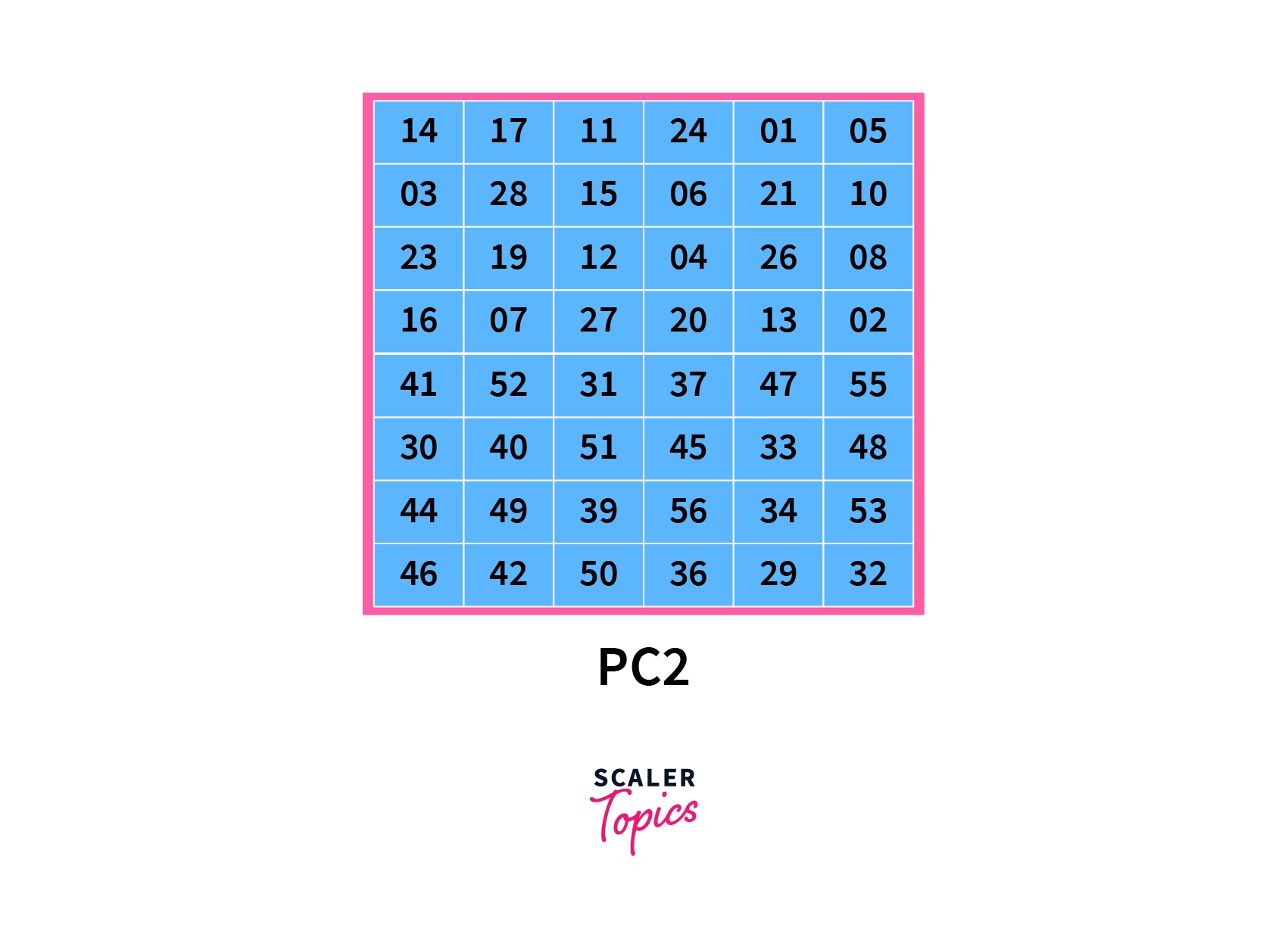
Similar to the previous permutation, the key is shuffled in such a way that the new position of the key bit is derived as indicated by the table.
Hence the 14th bit of the key is placed at the first position of the new permuted key, the 17th bit of the key is placed at the second position of the new permuted key..so on and so forth. On further inspection, we can see that the newly generated key has only 48 bits, unlike the previous keys that generated 56 bits. This process is called compression permutation.
The top half of the table contains numbers from 1 to 28, and the bottom half contains numbers from 29 to 56. This ensures the left and right halves of the resulting subkeys are separate.
Now, we have derived 16 different subkeys for each of the DES rounds. Now, we can move on to see how the encryption of the plaintext happens using the DES algorithm.
Encryption Process in DES Algorithm
The encryption process of plaintext using the DES algorithm is as follows:
- Initial Permutation Function:
Just like what we did with the key, the plaintext is broken into blocks of 64 bits each. The plaintext is the data that needs to be encrypted and transmitted from sender to receiver. It is also padded if the last block is not the required 64 bits long.
Then, it is fed to the initial permutation function, which confuses the text before any operation is done on it. The IP (Initial Permutation) does not contain any cryptographic value.
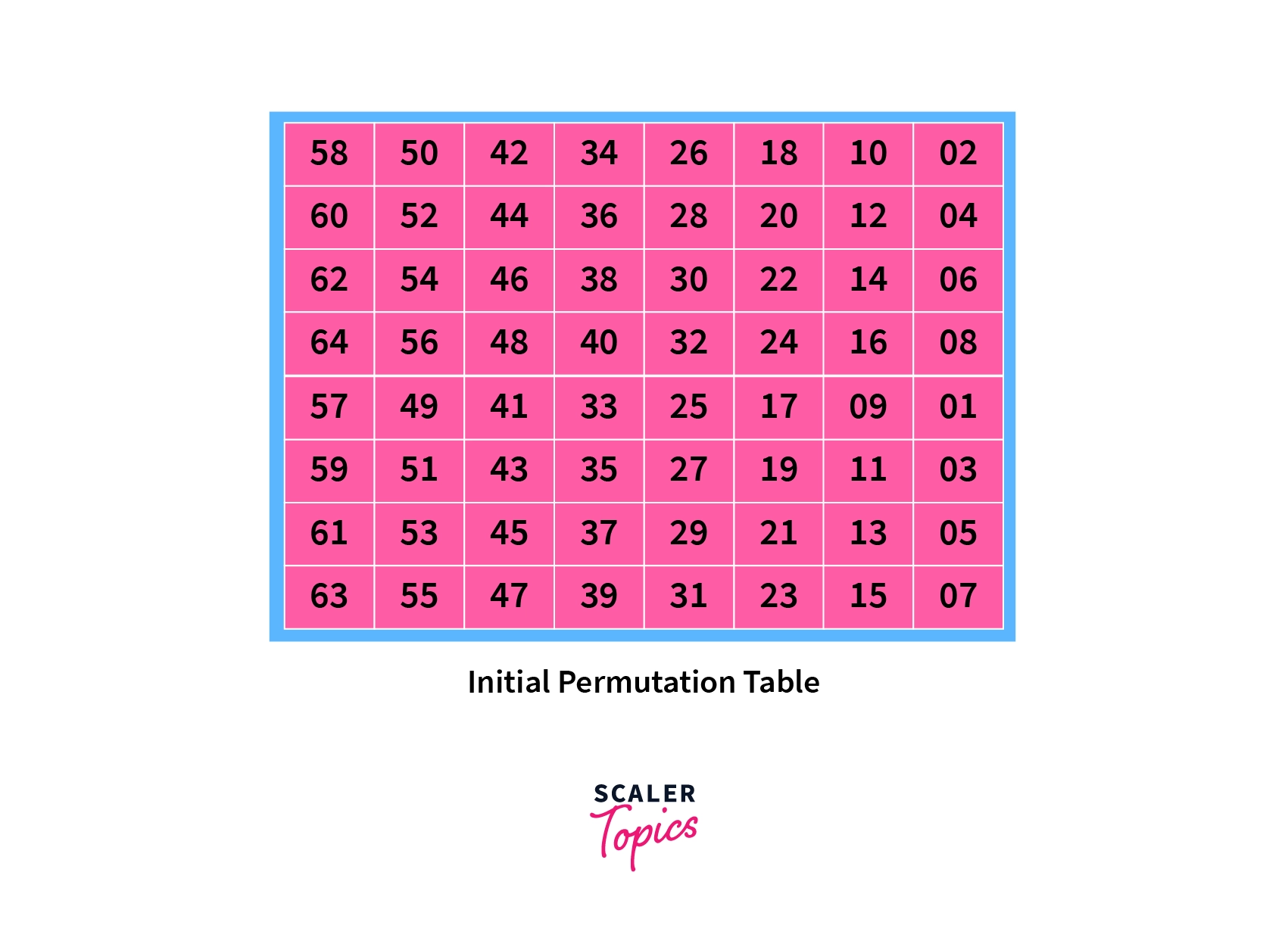
The permutation is done similar to what we did with the key, and the bits of the binary coded message are arranged following the Initial Permutation table.
The output of this step is taken as input for the next step:
-
Splitting the Blocks:
Once the IP process is finished, the data is split into 2 halves, a left block L0 made-up of 32 bits, and a right block R0, made up of 32 bits.
After the splitting of the blocks, we move to the next function. In round one, the right half of the block is taken and undergoes the following steps:A)Expansion Permutation (E)
B)Key mixing (⊕)
C)Substitution (S1, S2,...,S8)
D)Permutation (P)
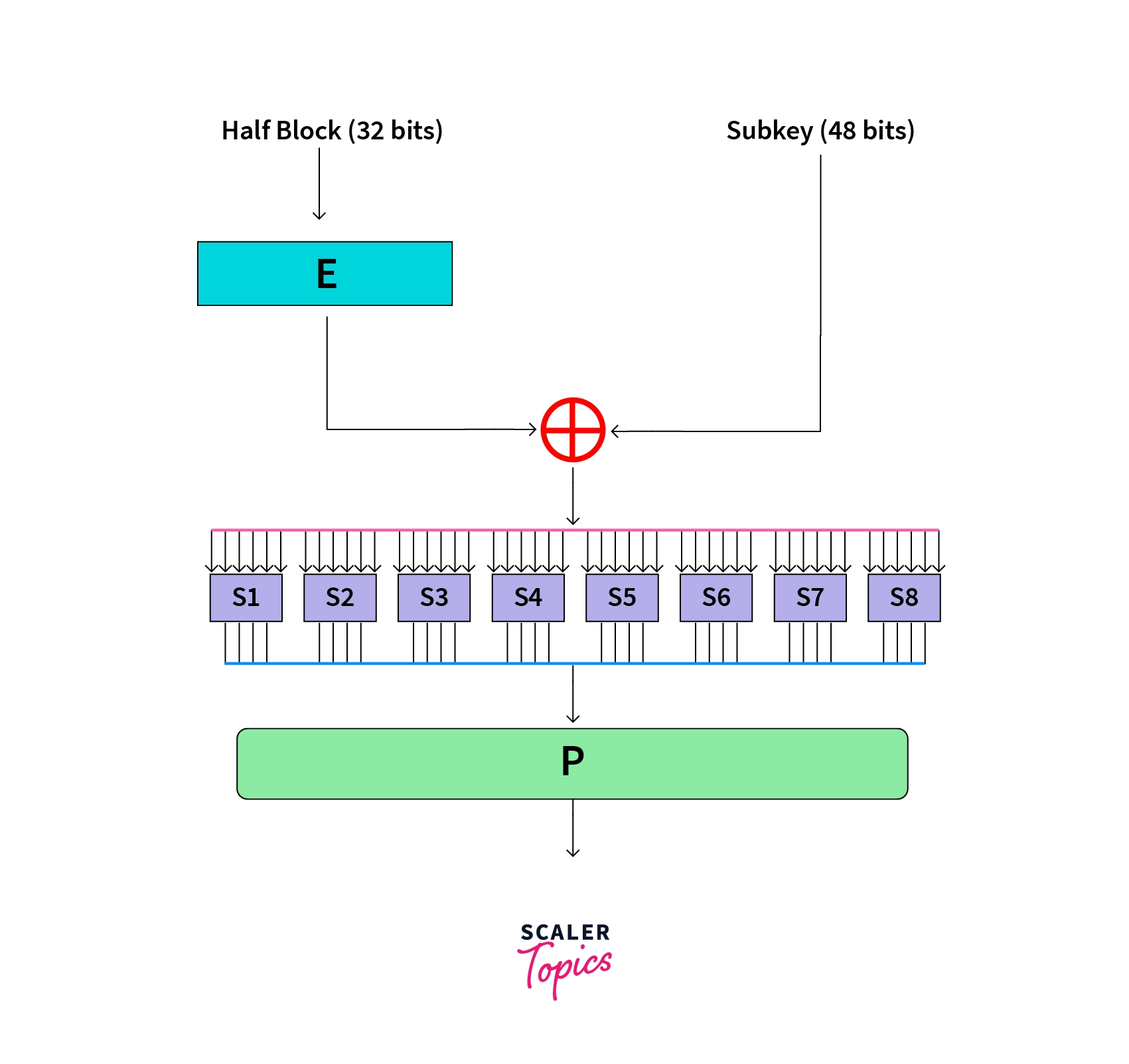
A) Expansion Permutation (E):
Three things are accomplished by the expansion permutation, an important one being the avalanche effect, where one bit of input data directly affects the output of 2 different bits. This step also makes sure the right half has 48 bits, so that it has the same length as the subkey for the upcoming step.
An example of avalanche effect:
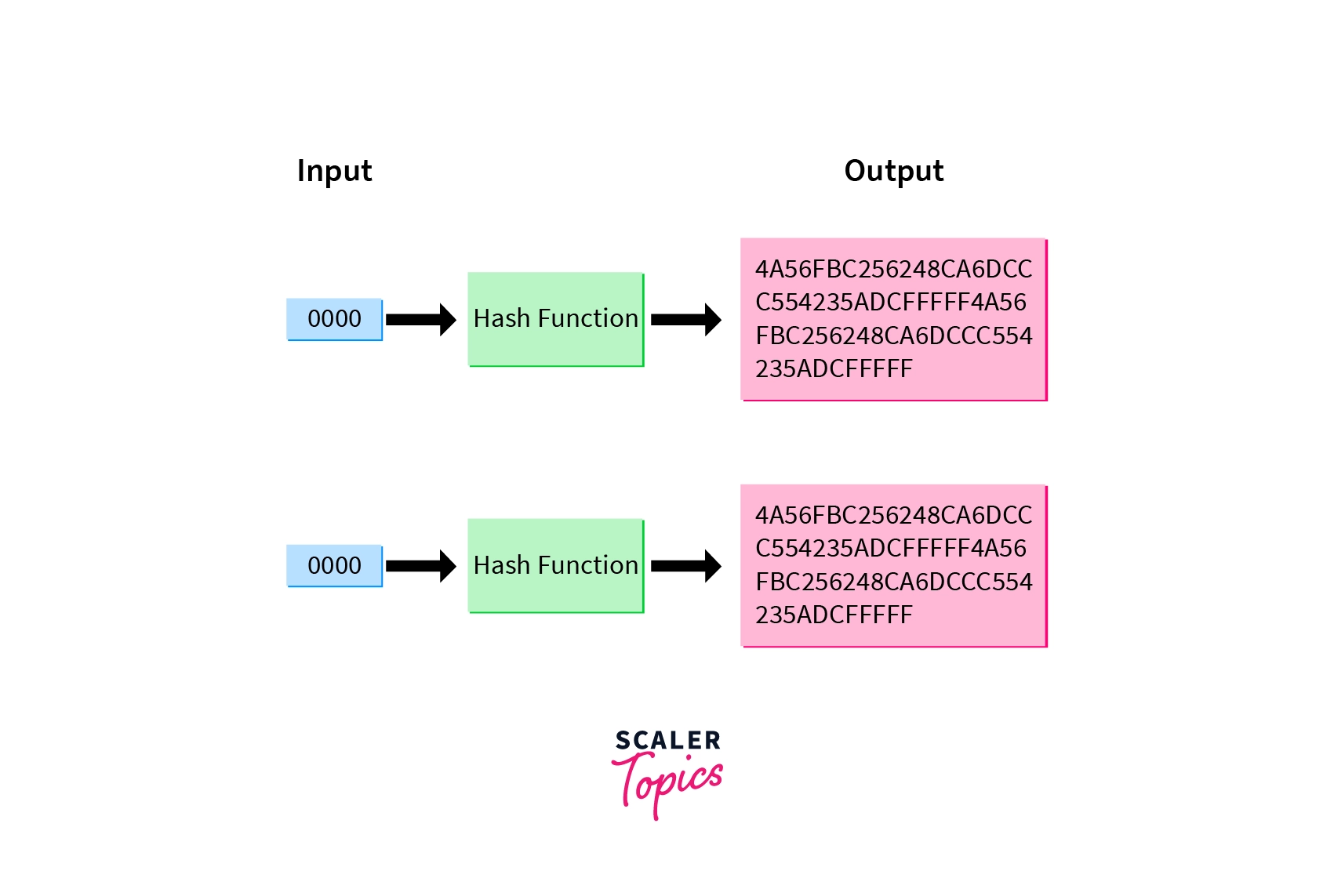
Another important outcome of the Expansion Permutation is that it permits the data to be squeezed together in the substitution operation by making the output longer than the input.
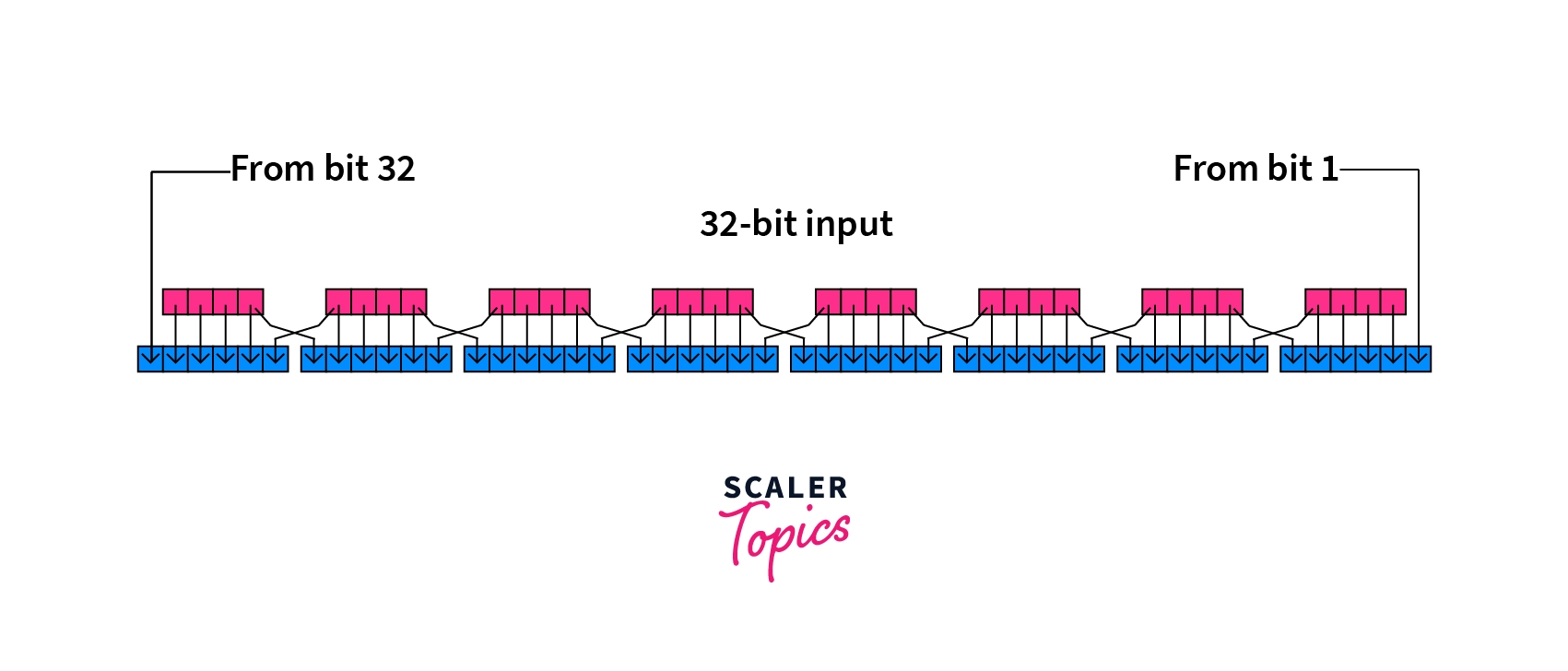
Next, the blocks are permuted once again using the following expansion function table:

On careful inspection, we can notice that a few blocks are repeated in the table. This is to expand the block from 32 to 48 bits.
B) Key Mixing (⊕):
Once we have expanded the block to 48 bits, we apply the subkey of the 1st round which we derived from the key scheduling we did before. The block is then amended by the subkey using the XOR table.
For example, if the last 8 bits of the expanded key is 01001011, then the key after the key mixing step becomes: 10110100.
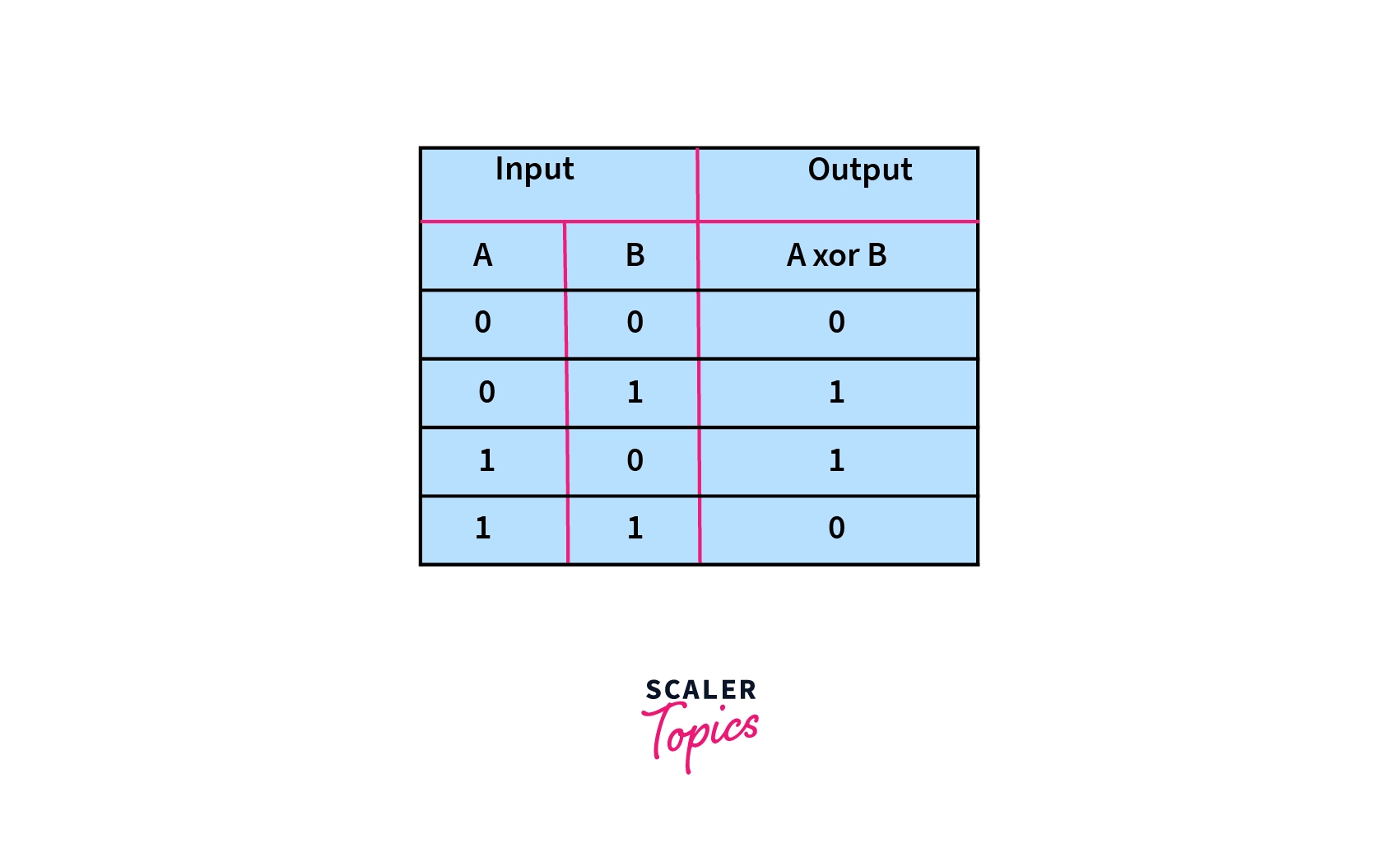
The resulting block is pushed to the next step.
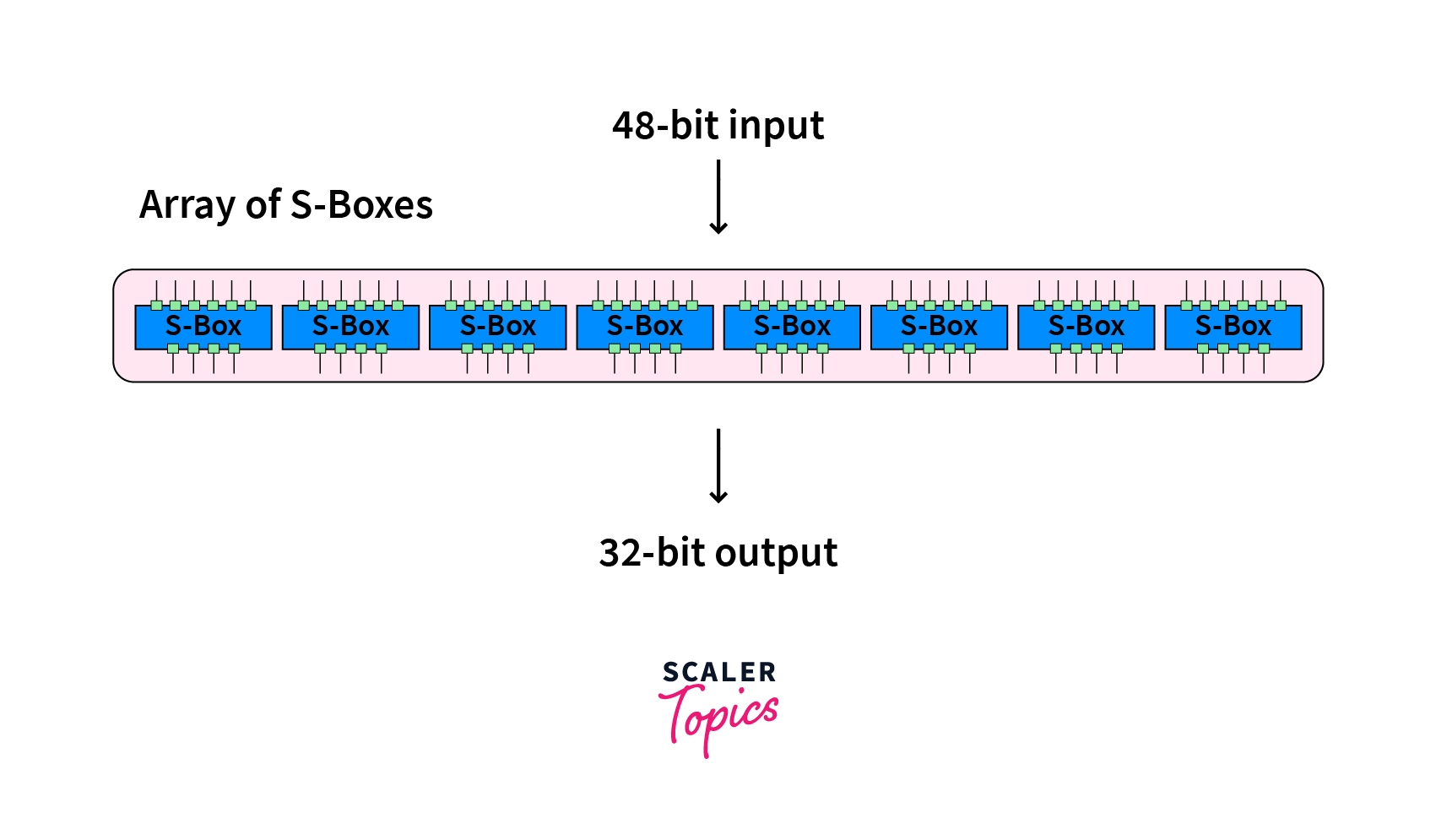
C) Substitution (S):
Substitution is used to make the data more complex so that it cannot be deciphered easily. 8 pre-made tables called substitution boxes or S-Boxes are used to transform each 6 bit input into a 4 bit output.
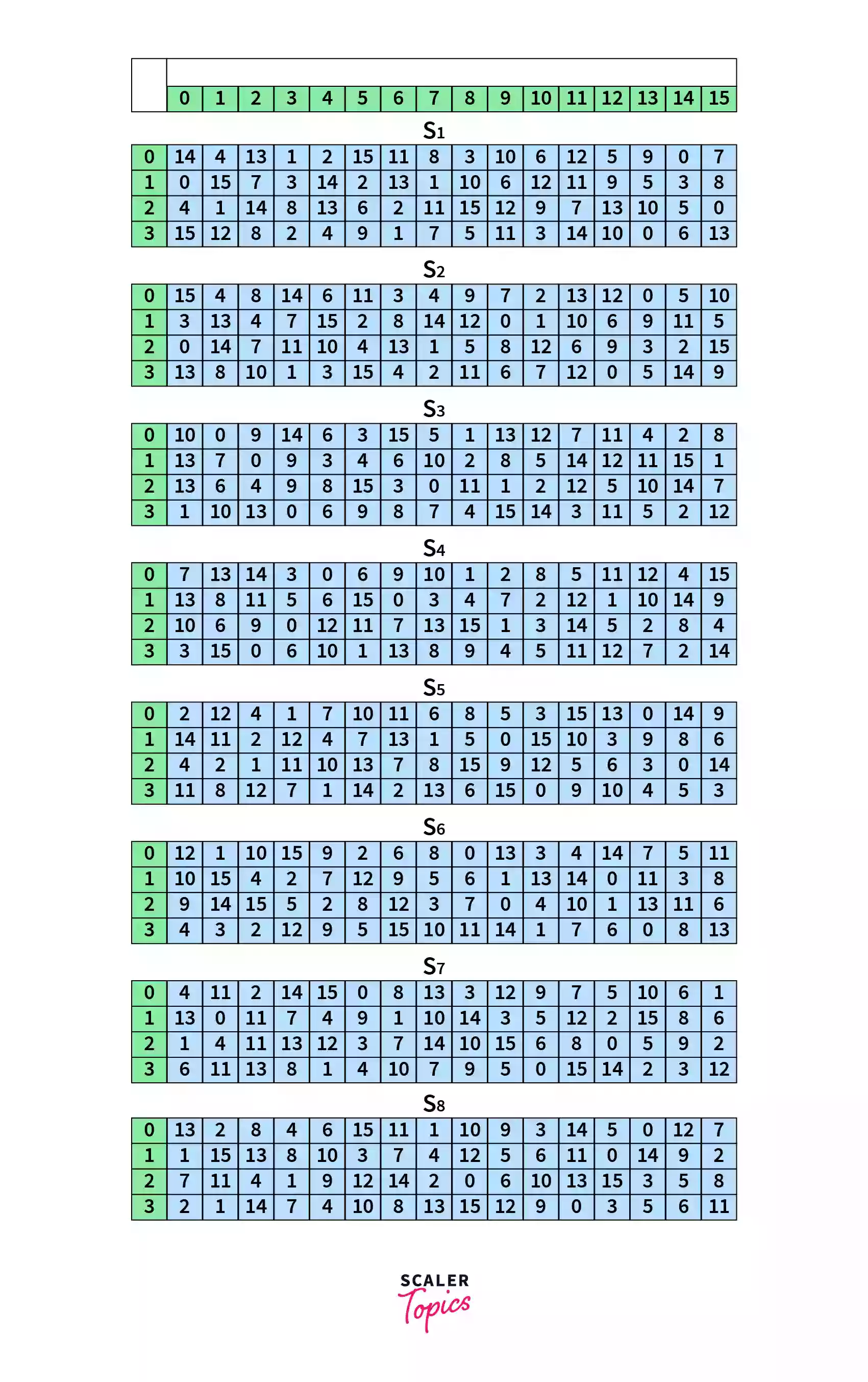
From the 6 bit input, the MSB and LSB is taken and converted to decimal number X. This number X gives us the row number of the S-box. Next, take the 4 bits in the middle of the input and convert that into decimal number Y. This number Y gives us the column number to look at. Now, take the number from the S-Box corresponding to the X row and Y column, and convert this into a 4 bit binary number. Hence, we have successfully converted a 6 bit input into a 4 bit output.
For example, let’s assume that the 6 bit output from the previous step is B = . We’ll represent the bits with .
To find the row number, we first take and combine the MSB and LSB () which gives . We then convert this to decimal, which gives us , meaning row 3.
For the column number, we take , which is . On converting to decimal, we get , or column 7.
Hence for the number, we substitute it with the number from row 3 and column 7, which gives 7.
We choose which substitution box to choose from based on the location of the bits. Here in our example, the 6 bits are from the beginning of the output from step (B). Hence, we take the first S-box.
D) Permutation (P):
Finally, the F function is again permuted using the below permutation P table:
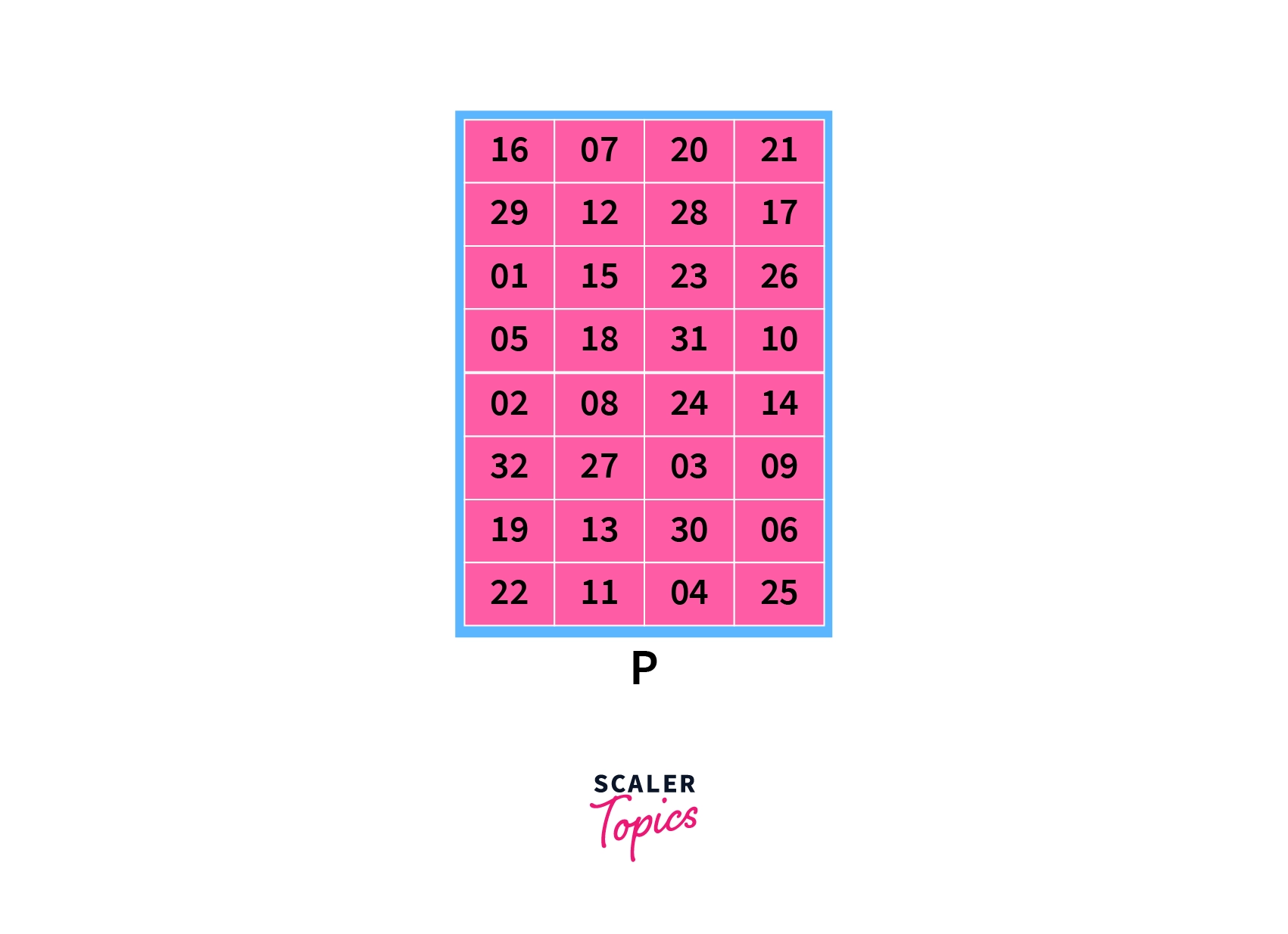
Now, we have finished all steps of the F function. This value that we have derived (the encrypted data) is known mathematically as f(R0, K1). This means that the outcome is a function of the initial right side of block R0 and subkey of the first round.
Now we take this value and do the following steps:
iii) XORing with the Left Block: Now, we take the left half of the block we left previously, and XOR it with the f(R0,K1) block that we got after permuting in the previous step. This gives us R1, the result of the first round of processing.
iv) 15 more times!: The above 3 steps are run 15 more times to complete 16 rounds of processing. The next diagram gives a visual representation of the processing of the blocks:
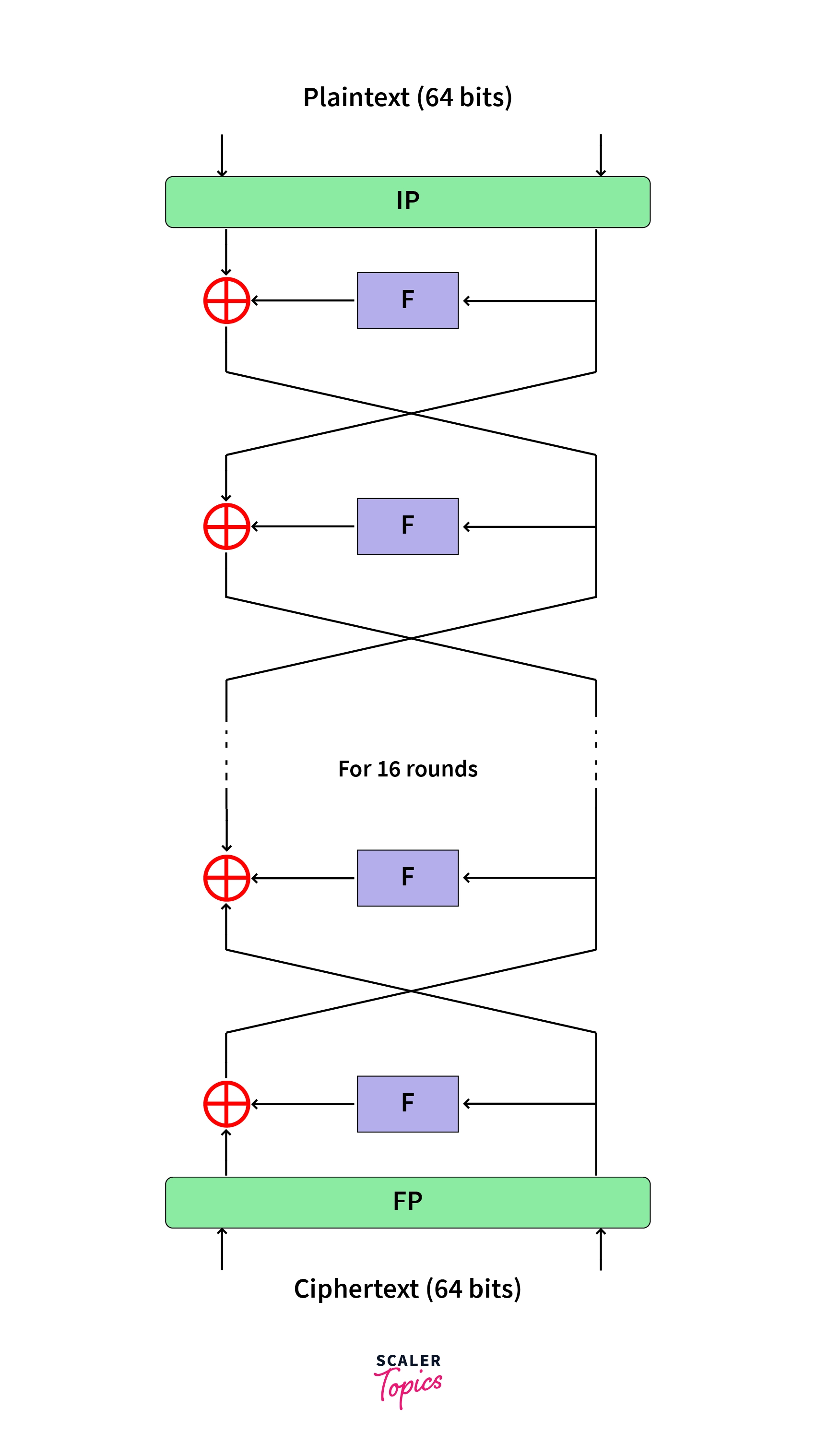
The formula is as follows:
where,
= left half of the block during round number ‘n’
= right half of the block during round number ‘n’
f = f function
= subkey for round n
v) Final Permutation: Finally, the result of the final round is permuted one last time following the given table:
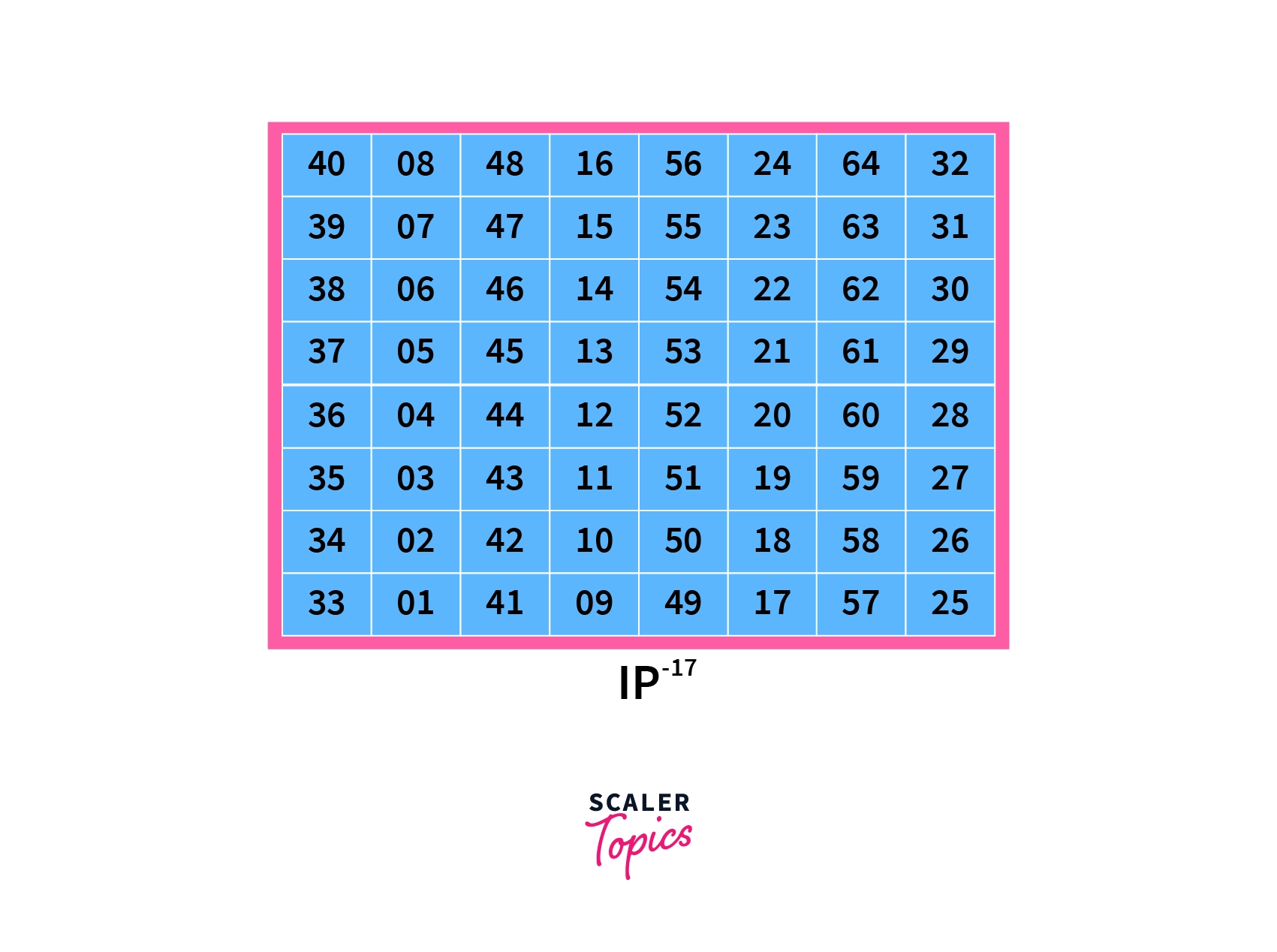
Here, the table is the inverse of the initial table P. Finally, the output of this inverse permutation table is the ciphertext of the DES algorithm.
A. bird’s eye view of the entire process is as follows:
Decryption Process in DES Algorithm
Now, I’ll explain the decryption process for DES:
The algorithm has a Feistel structure which makes the decryption straight and simple. Decryption takes place almost similar to the encryption process, the only difference is that the subkeys are applied in reverse.
First, the data goes through the initial permutation ΙΡ, and the block is split into two. The right half is carried through the F function. But this time, the 16th subkey is registered and everything else goes on as usual. The left side of the resulting block is XORed once the output through the F function is received. The process is repeated by taking the subkeys in reverse order of encryption. Finally after the 16th round, the plaintext is received.
DES Modes of Operation
While the DES algorithm provides encryption of plaintext, its effective key length of only 56 bits means that it finds itself vulnerable to a variety of brute force attacks, especially in today’s world where cloud computing and supercomputers provide processing powers that far exceed computers available during the 1970’s, back when the DES was designed.
Hence for all practical purposes, the DES algorithm was used along with different modes of operations based on the applications and uses.
Some of the most important modes of operation include:
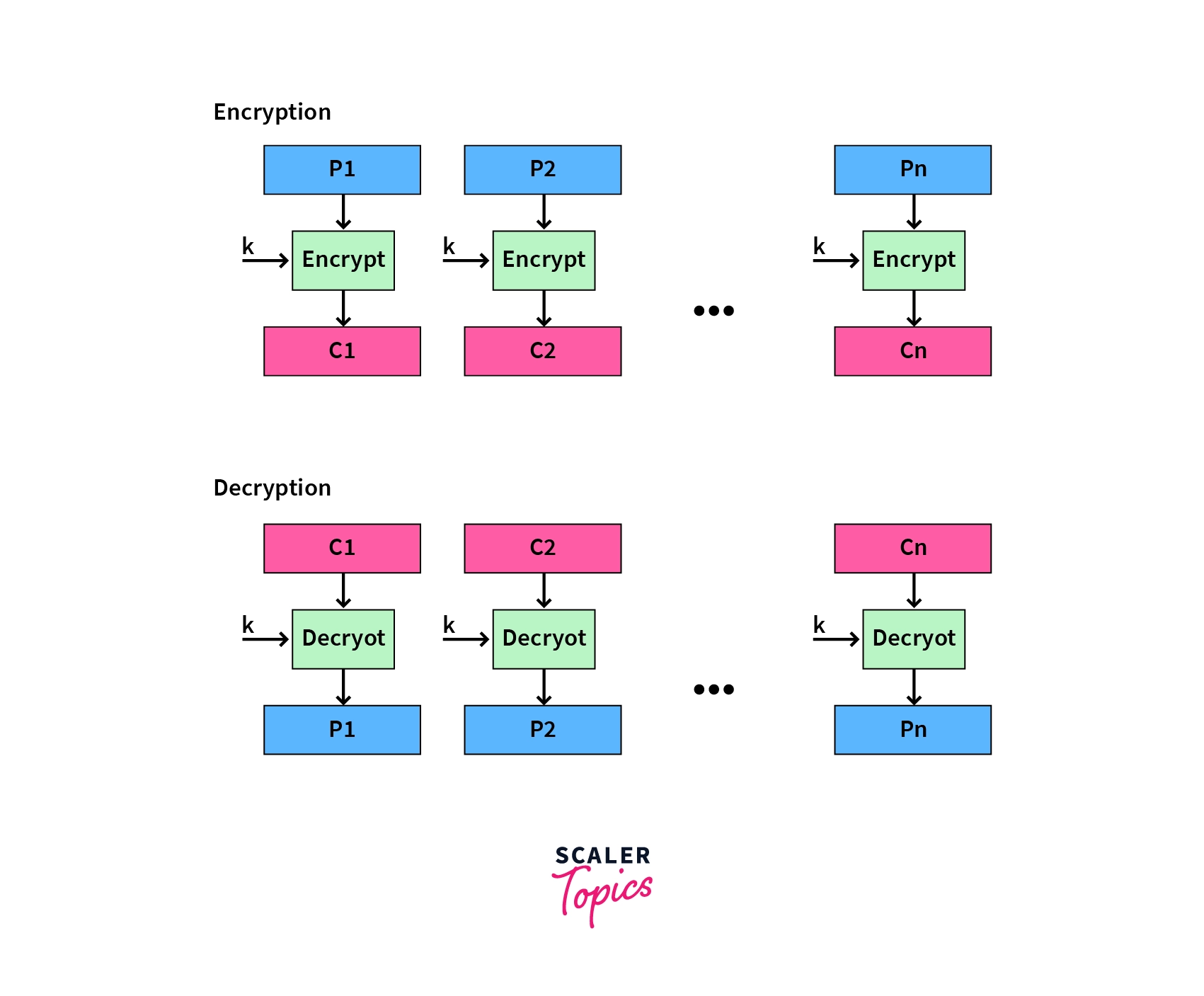
- Electronic Code Book (ECB): This is the simplest mode of operation. Input plaintext is taken as blocks, and each block is directly encrypted using the DES algorithm to create a block of ciphertext.
- Cipher Block Chaining (CBC): This is built upon ECB, providing better security than it. Here, the previous cipher block is given as an input to the next encryption cycle, after it is XORed with the plaintext. Essentially,
Cipher Block (1) = Cipher Block (0) ⊕ PlainText Block (1) + Key.
In the figure below,
: Plaintext during round number ‘x’. IV: The initialization vector. K: The subkey. : Ciphertext during round number ‘x’

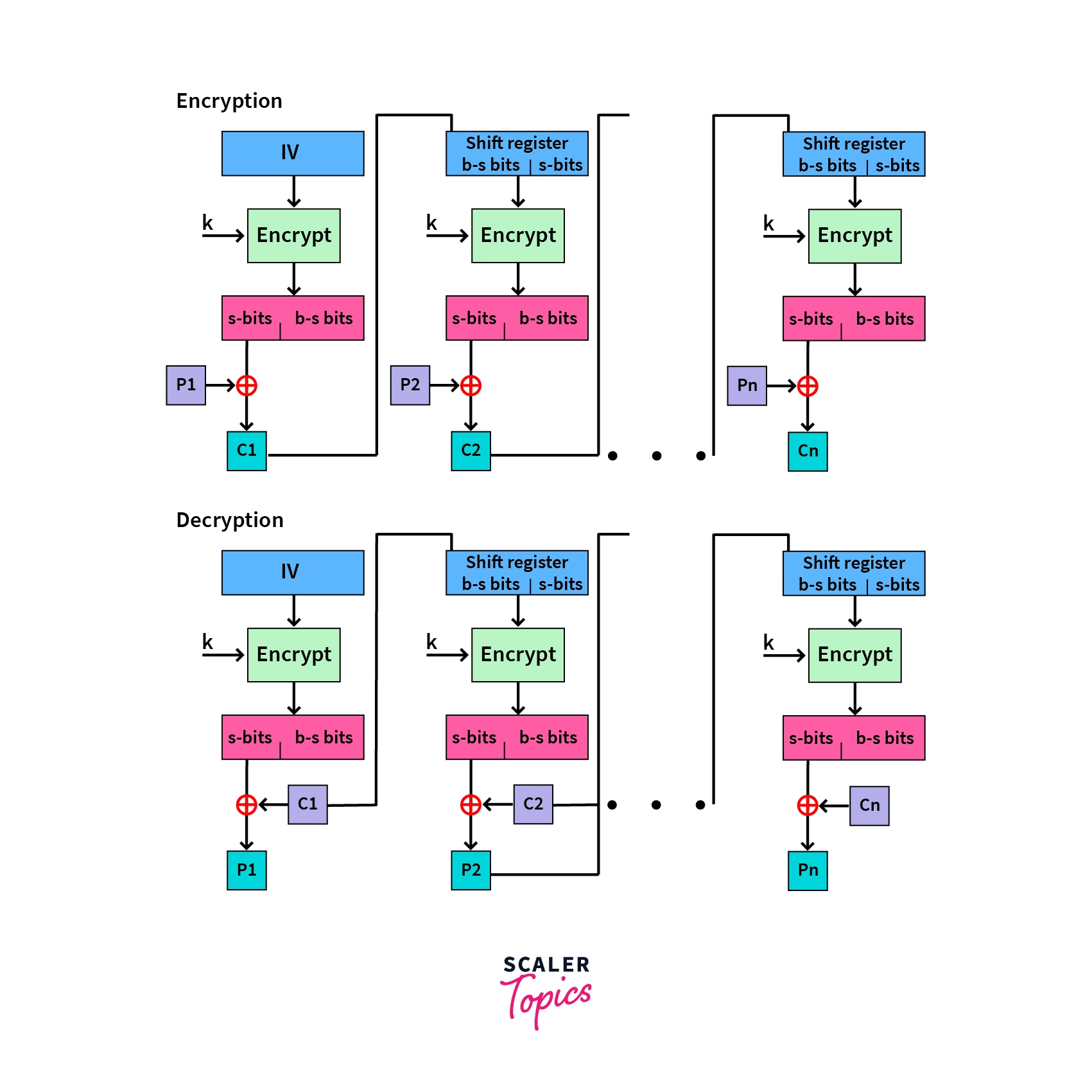
- Cipher Feedback Mode (CFB): In this mode, a special variable to initiate the encryption, called an Initialization Vector (IV), is used. The first encryption utilizes the IV, and all subsequent encryptions utilize the output of the previous encryptions as an input.
The output of each round is divided equally into s-bits on the left and b-bits on the right. The s-bits are then taken and XORed with the plaintext during the next round’s encryption.
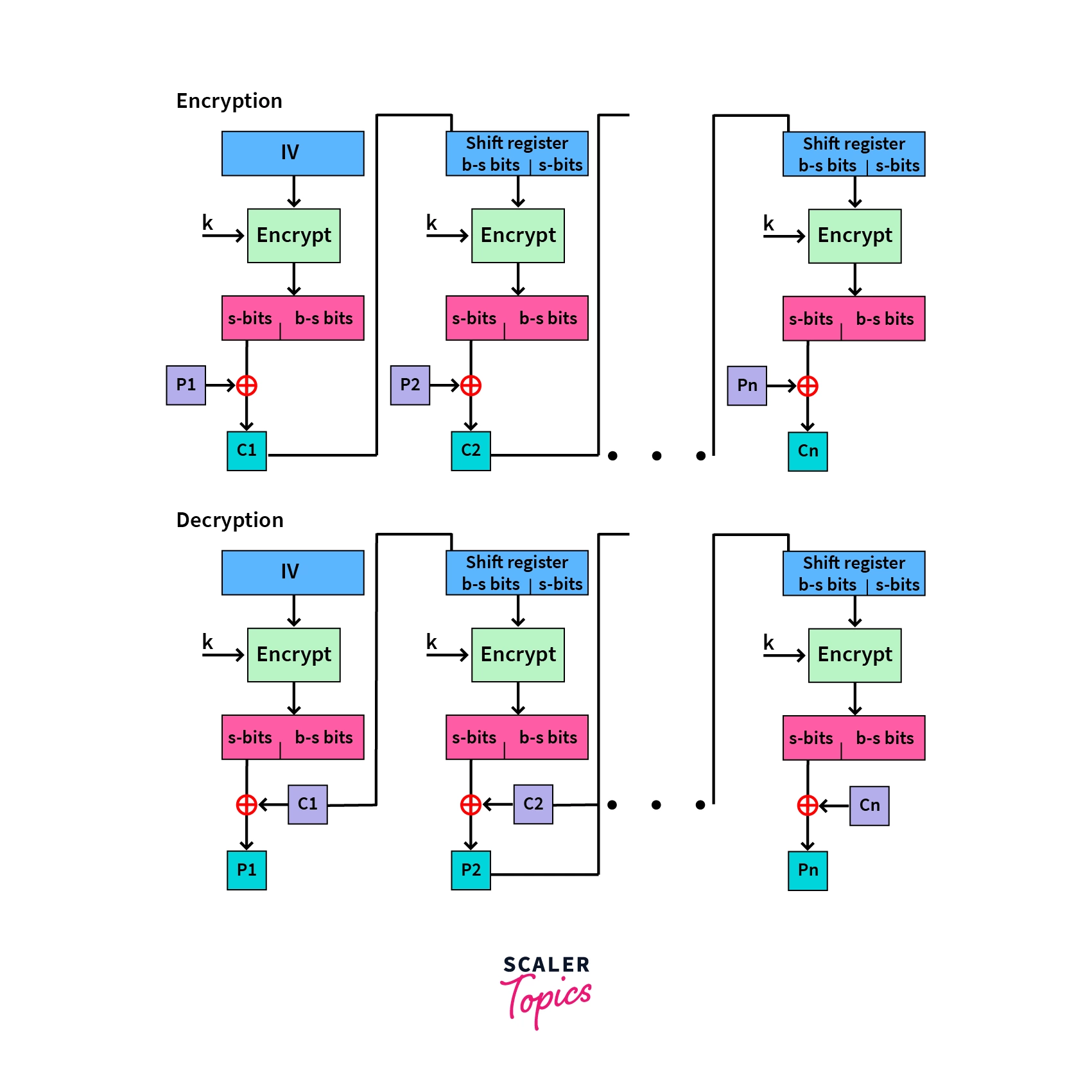
- Output Feedback Mode (OFB): It follows a similar process to the Cipher Feedback, with the only difference being that the output is sent to the next round as feedback, instead of the s-bits.
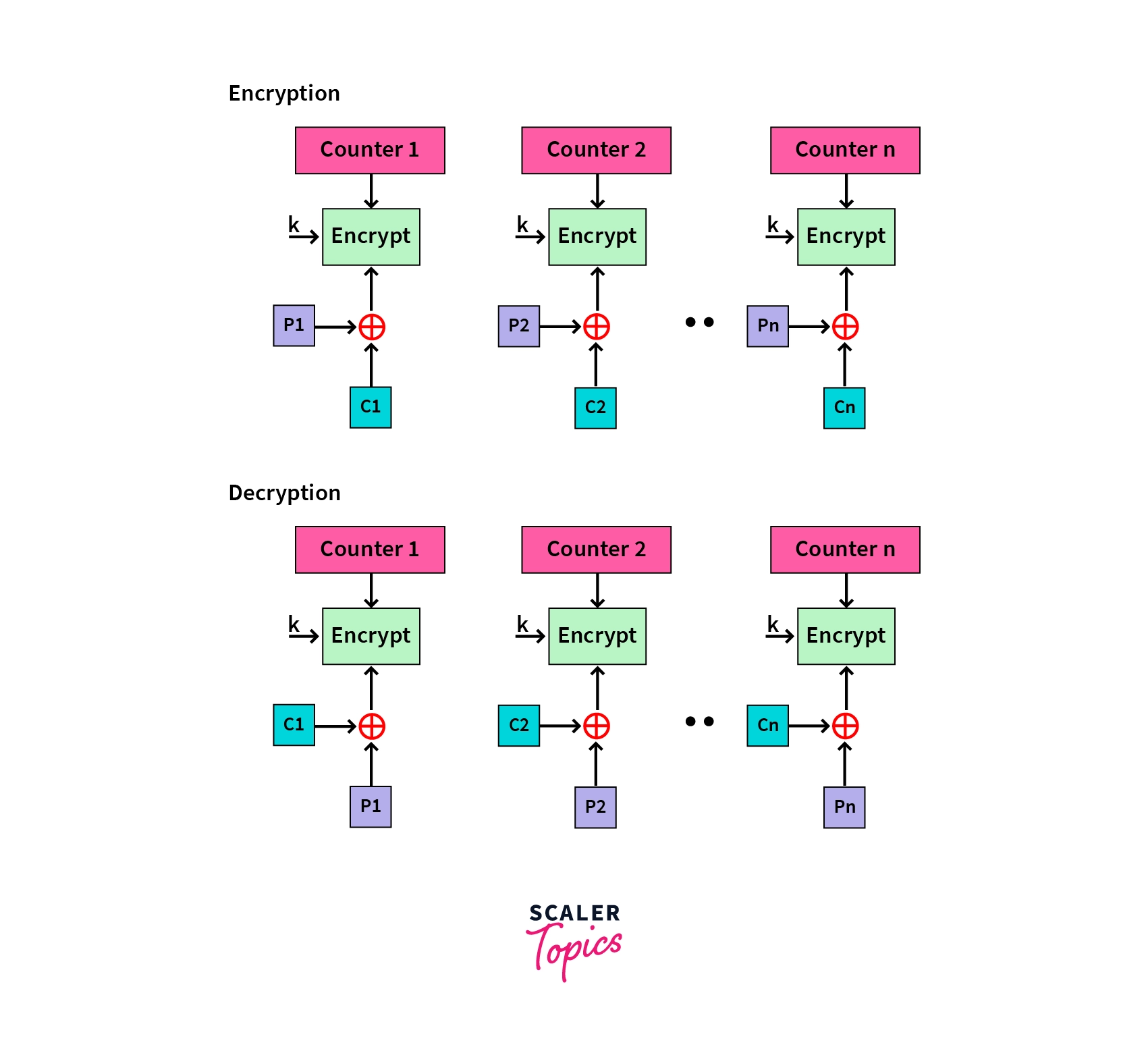
- Counter Mode (CTR): This is a simple counter based on block ciphers. A counter value is encrypted with the subkey given as input and XORed with the plaintext. The counter value is independent of any feedback, hence can be implemented in parallel
Implementations and Testing of DES Algorithm
The C++ code to implement the DES algorithm goes as the following:
- Key Generation:
The algorithm involves 16 rounds of encryption involving 16 different subkeys.
- Encryption of Plaintext to obtain Ciphertext
The plaintext to be encrypted is divided into 2 equal halves, and undergo 16 rounds of encryption. They’re then combined to create the ciphertext.
- Decryption of Ciphertext to get back Plaintext:
Conclusion
-
The DES algorithm is no longer in popular use because of its effective key length of 56 bits, which can be broken with brute force with the technology available today in a matter of minutes.
-
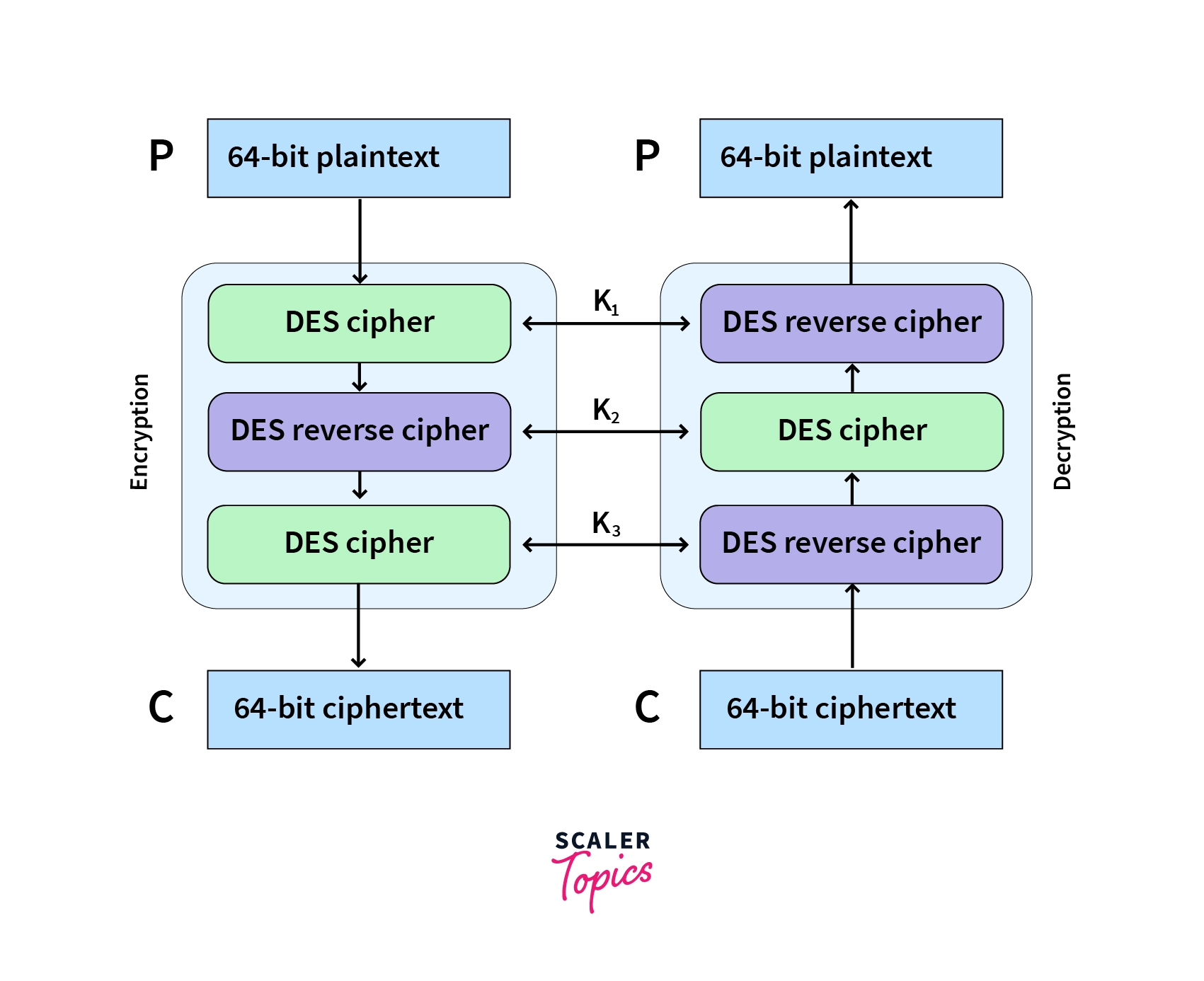
An improvement of the algorithm, called the Triple DES or 3DES for short, was created to overcome this. It is essentially the DES algorithm run thrice, hence expanding the key space three times. But even this suffered from the fatal flaw of man-in-the-middle attacks, where attackers can simply listen to a part of the key and figure the rest out.
-
The DES algorithm was used by HBO with their ‘Videocipher II’, a TV satellite scrambling system. IBM too used DES to encrypt their PIN verification systems during the 1970’s.
-
Nowadays, an algorithm called the Advanced Encryption Standard, or the AES, is in widespread use. It is also a block cipher like DES, but uses a 128 bit key and follows different functions to create ciphertexts. There are currently no known attacks on it.
