Detect Cycle in Undirected Graph
FREE
Overview
Given an undirected graph containing ‘n’ nodes and ‘e’ edges. Determine whether or not the graph contains a cycle.
Takeaways
Worst-case time complexity of Depth first search for detecting the cycle in undirected graph is O(n) where n is the number of nodes.
Example of problem.
Consider the following image.
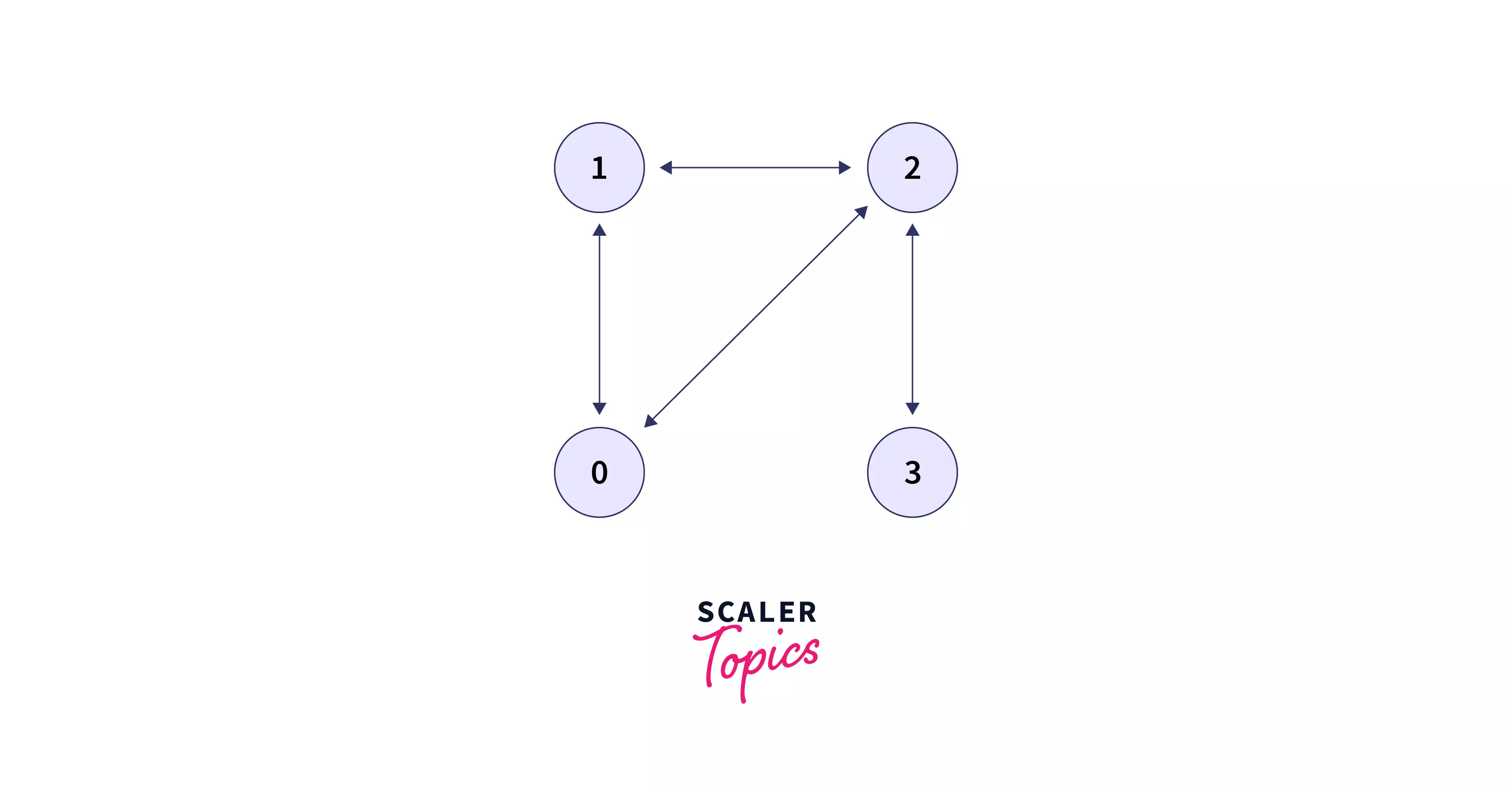
It shows an undirected graph with a cycle. Now have a look at the following image.
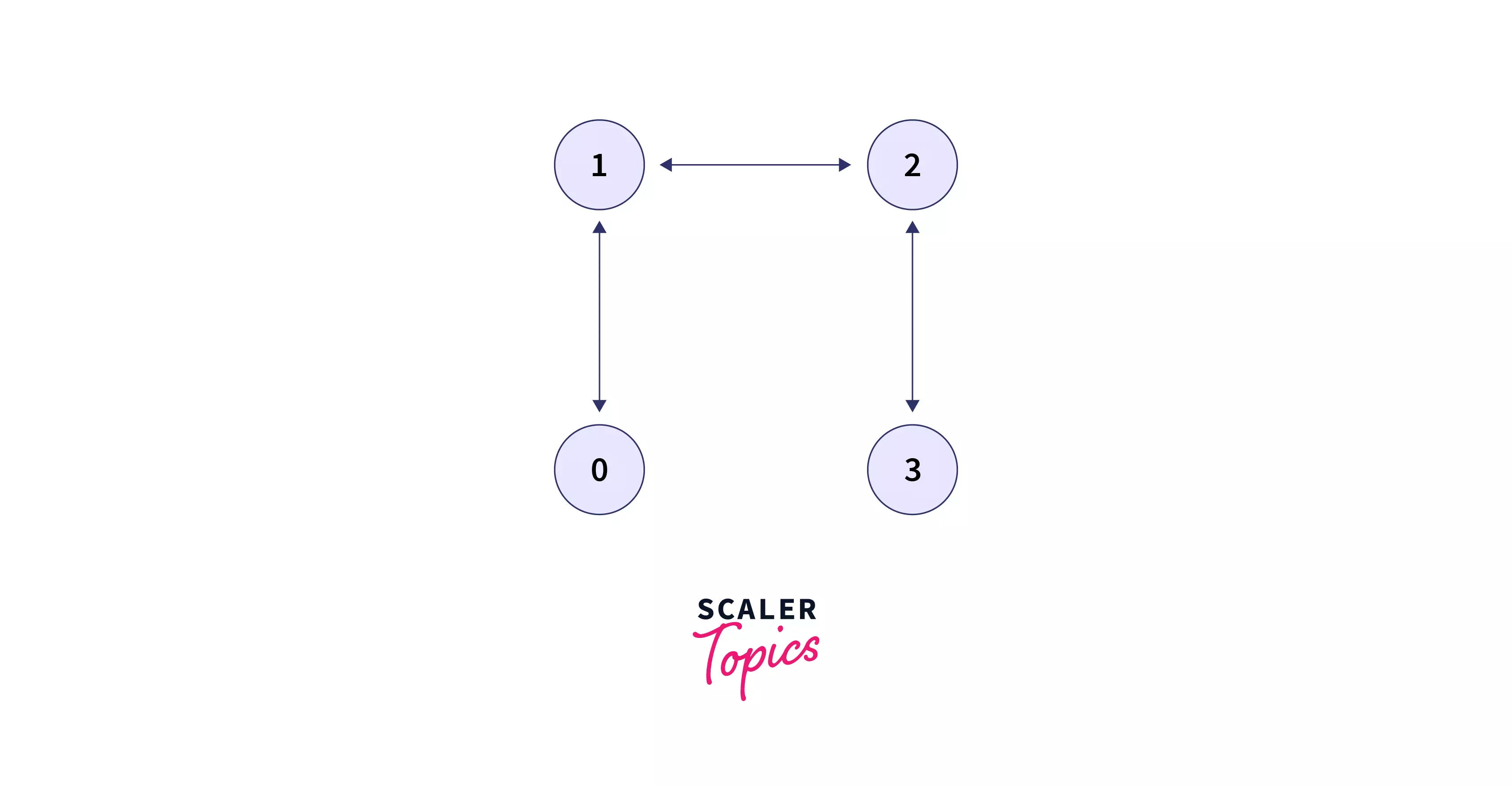
It shows an undirected graph without any cycle
Build an AI-First Career, Master the Complete Skillset
Choose from our industry-leading programs designed for career success
Modern Software and AI Engineering Program
Master full-stack development with AI integration
+1000 moreModern Data Science and ML with specialisation in AI
Advanced data science techniques with AI specialization
+1000 moreAdvanced AIML with Specialisation in Agentic AI
Deep dive into AIML with focus on Agentic systems
+1000 moreDevOps, Cloud & AI Platform Engineering
Build and manage AI-powered cloud infrastructure
+1000 moreAI Engineering Advanced Certification by IIT-Roorkee
Premier AI engineering certification from IIT-Roorkee
AI Forward Deployed Engineer Program
Full-stack engineering, production AI and client-facing consulting
+1000 moreExplanation of the problem.
We have to detect cycle in undirected graph. In a graph, any path with 1 or more duplicates of any node(s) present in the path is known as a cycle A graph containing a cycle is called cyclic. For example, an edge from a node itself is a cycle. It is a trivial case often referred to as a “self-loop”. A path that ends at the same node that it begins from also forms a cycle.
Constraints for the problem
The input will be as follows: The first line contains an integer ‘n’, the number of nodes numbered from 1 to n. 1 <= n <= 10^5 The next line contains another integer ‘e’, the number of edges. The next e lines contain space isolated integers ‘u’ and ‘v’, which represent an edge between nodes numbered u and v respectively. The output must be of the form:
If the graph is cyclic.
Otherwise.
First approach: Depth First Traversal
We use depth-first search (D.F.S.) to construct a solution for this problem. We run a sequence of DFS in the graph. Initially, nodes are labeled 0 (zero) which implies the node is unvisited. From each unvisited node, begin the DFS, label the node visited with 1 while entering, and label it 2 on exit.
If DFS moves to a node labeled 1, then we have discovered a cycle. It is to be noted that since the graph is undirected, the edge from a node to its parent must not be considered. The cycle can itself be reconstructed using the parent array. Implementation:
1. C++:
2. Java:
3. Python:
Input:
Output:
Analysis of time complexity
The worst-case time complexity of this algorithm is O(e) where e is the number of edges.
How Scaler Transformed Careers in Different Fields
Scaler learners achieved 2.5x salary growth with average post-Scaler CTC reaching ₹23L.
Google
Amazon
Microsoft
Flipkart
Adobe1200+ moreHOW?
We perform a basic depth-first search in this algorithm, which at most will run all the edges. There will not be repetitive recursions (for the same edges) because we keep track of visited edges.
Analysis of space complexity
The worst-case time complexity of this algorithm is O(n) where n is the number of nodes.
HOW?
We make only 2 arrays of size n.
Second approach: Breadth-first search
The logic used in this second approach to detect cycle in undirected graph is quite similar to the one used in the previous (dfs) approach. But this (bfs) approach differs from it in that we use bfs in place of dfs for exploring the graph. Implementation:
Turn Learning into Career Growth
1. C++
2. Java
3. Python
Input:
Output:
Analysis of time complexity
The worst-case time complexity of this algorithm is O(e) where e is the number of edges.
HOW?
We perform a basic breadth-first search in this algorithm, which at most will run all the edges. There will not be repetitive entries of nodes in the queue (for the same edges) because we keep track of visited edges.
Analysis of space complexity
The worst-case time complexity of this algorithm is O(n) where n is the number of nodes.
HOW?
We make only 2 arrays of size n.
Conclusion
- An undirected graph is a set of nodes and edges, such that an edge signifies bidirectionality.
- Any path with 1 or more duplicates of any node(s) present in the path is known as a cycle A graph containing a cycle is called cyclic.
- We can solve the problem of detecting a cycle in an undirected graph by using dfs or bfs.
