DFS (Depth First Search) Program in C

Overview

Depth First Search is one of the major traversal techniques which is commonly used to traverse graphs and trees(a subset of graphs). According to DFS, the search should start from the root or starting node and a particular path must be traversed to its depth before traversing the other adjacent nodes. It goes deep down to a node's descendants or adjacents in a single direction and continues to traverse other nodes when there is nothing remaining in the depth.

What is the DFS (Depth First Search) Program in C?

Digression:

Let's start the discussion from the very beginning, we use a data structure to store our data, and then we further create some algorithm to manipulate that data and in the end, we receive some insights or results as output. So to make the algorithm work on the data structure it is necessary to entirely explore/visit the data structure to see the actual stored data in the data structure, for example, as you might know from the concept of arrays it is simple to traverse the array by indexing operator but what about when the data structure is not simple but complex and non-linear like trees and graphs, in these case the traversing techniques also becomes complicated.

The process of finding all vertices/nodes in a graph is known as graph traversal. The order of the vertices visited during the search process is also determined by the graph traversal. We have a few major standard techniques to traverse on non-linear tree and graph data structure they are majorly classified into the,

Breadth first traversal
Depth first traversal

Traversal in Graph

The traversal or searching begins with the arbitrary starting node, we can choose any node to be starting node as per our requirement all traversals would be a valid DFS traversal. After deciding on the starting node, explore any of the adjacent node of starting node, and before traversing the other remaining adjacent node of starting node the algorithm explores all possible adjacent nodes in the single path till its most possible depth. When there is nothing left to explore or can say all nodes are already visited, the algorithm reverts back to the starting node and then follows the same strategy to discover other remaining nodes which haven't been traversed yet. This paragraph would be more clear to you after visiting the algorithm section below.

Algorithm of Depth First Search

Here we will discuss the working of the Depth First Search Algorithm, you will get the exact idea of how things go on internally while executing a DFS program.

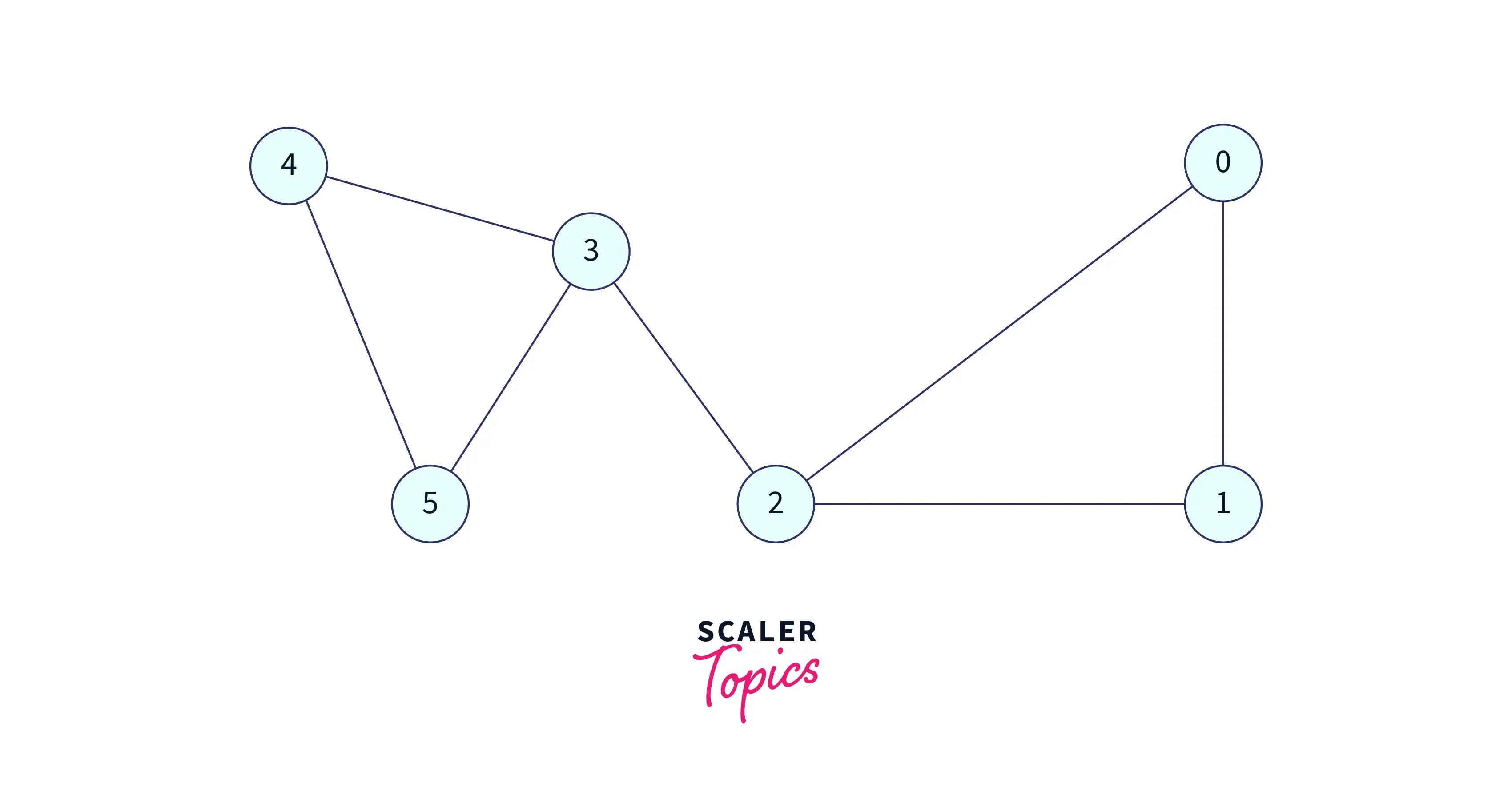
Sample Graph:

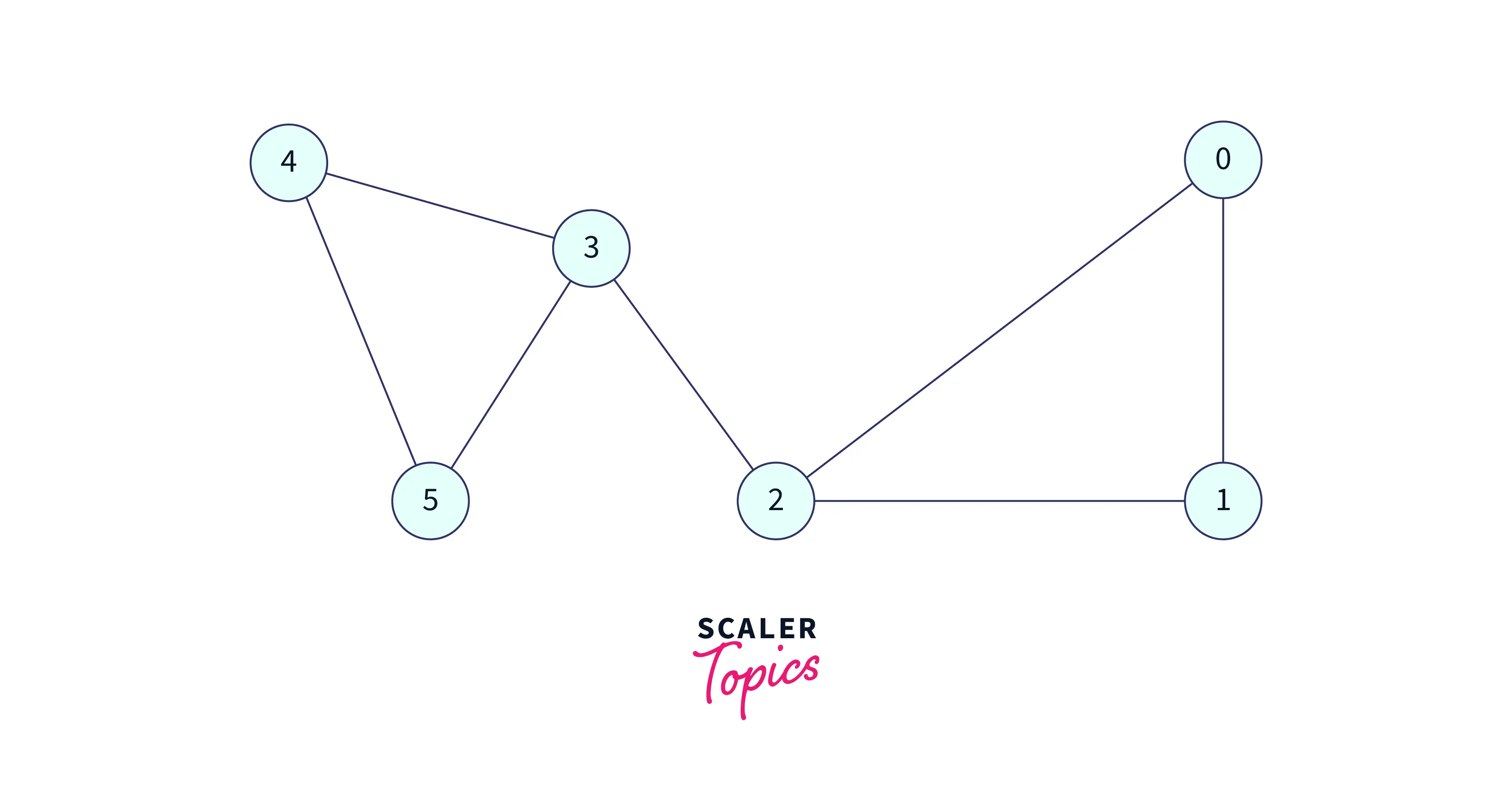
sample-graph-example

Start from a Starting Node, Consider 2 as a Starting Node, Visit 2 and add this to the DFS traversal,

node-2-as-dfs-traversal

We have 3 adjacent nodes to 2, let's visit the 3.

Note: If there are multiple nodes adjacent to the current node then it depends on how data is stored and how the algorithm is working to determine their order, but in the end, all of them will be considered valid DFS traversal

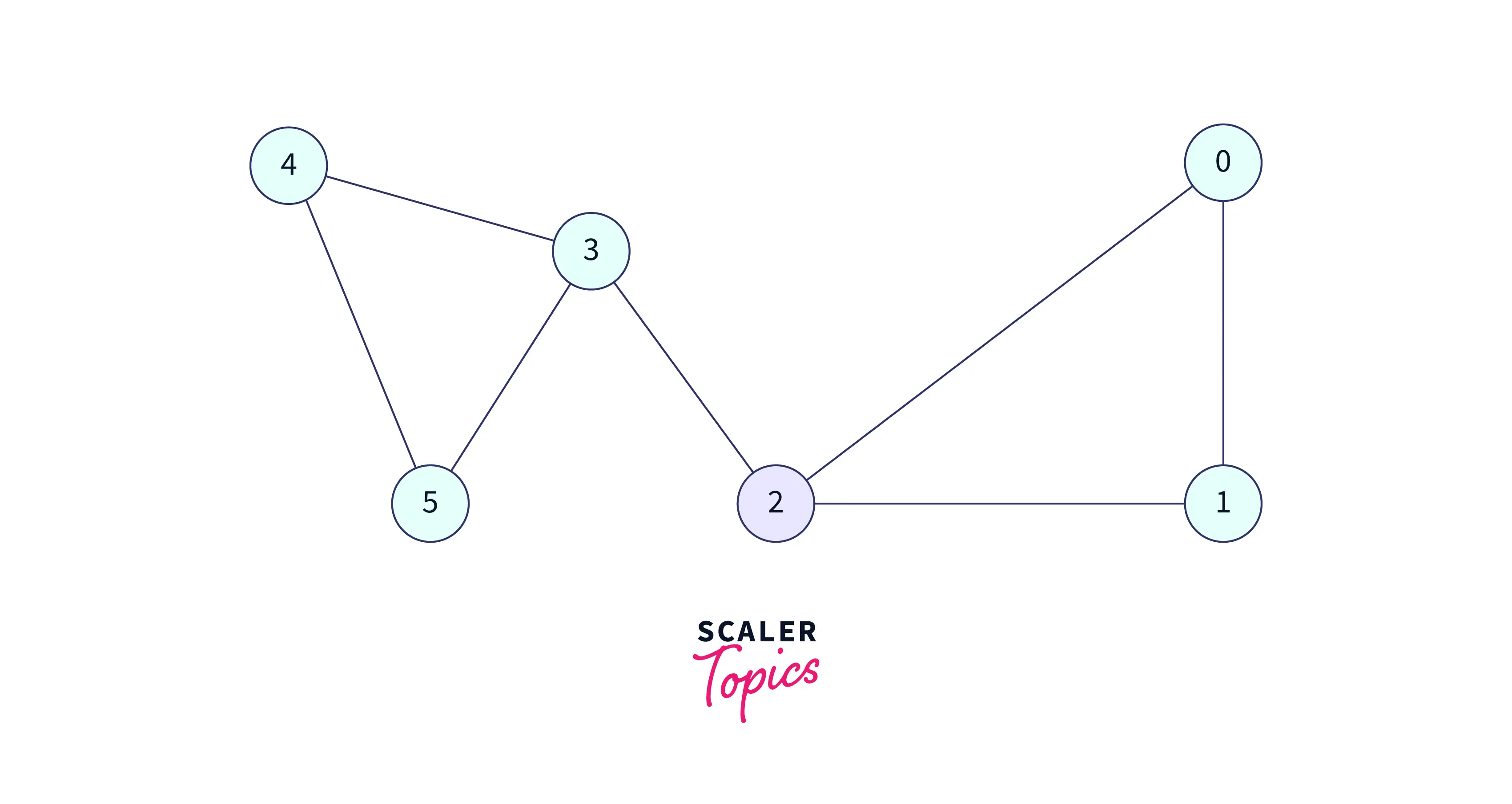
Visit 3 and add this to the DFS traversal,

adding-node-3-as-dfs-traversal

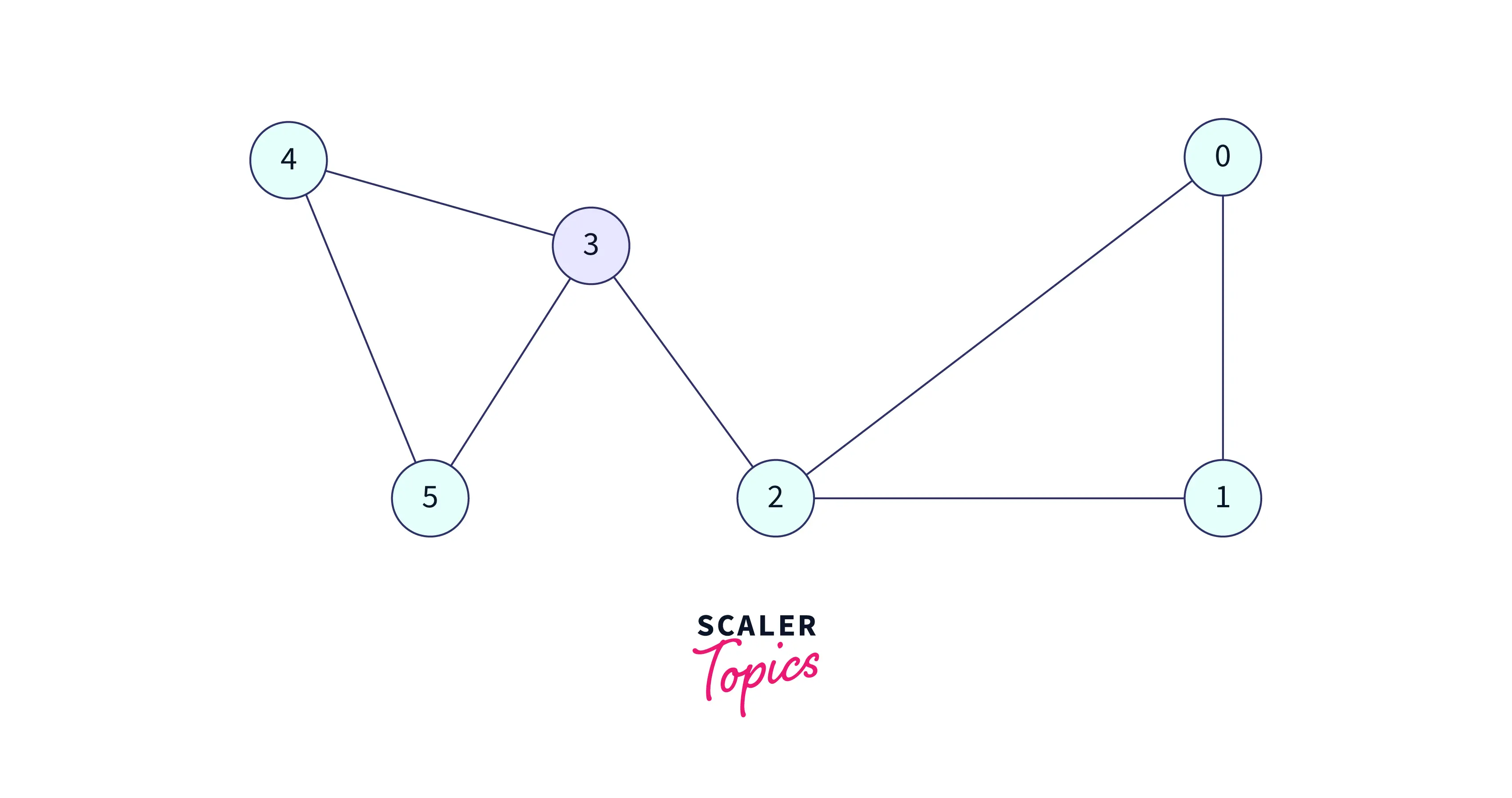
We have 3 adjacent nodes to 3, in which 2 have already visited so we have to select from 4 or 5, let's visit the 5. Visit 5 and add this to the DFS traversal,

adding-node-5-to-dfs-traversal

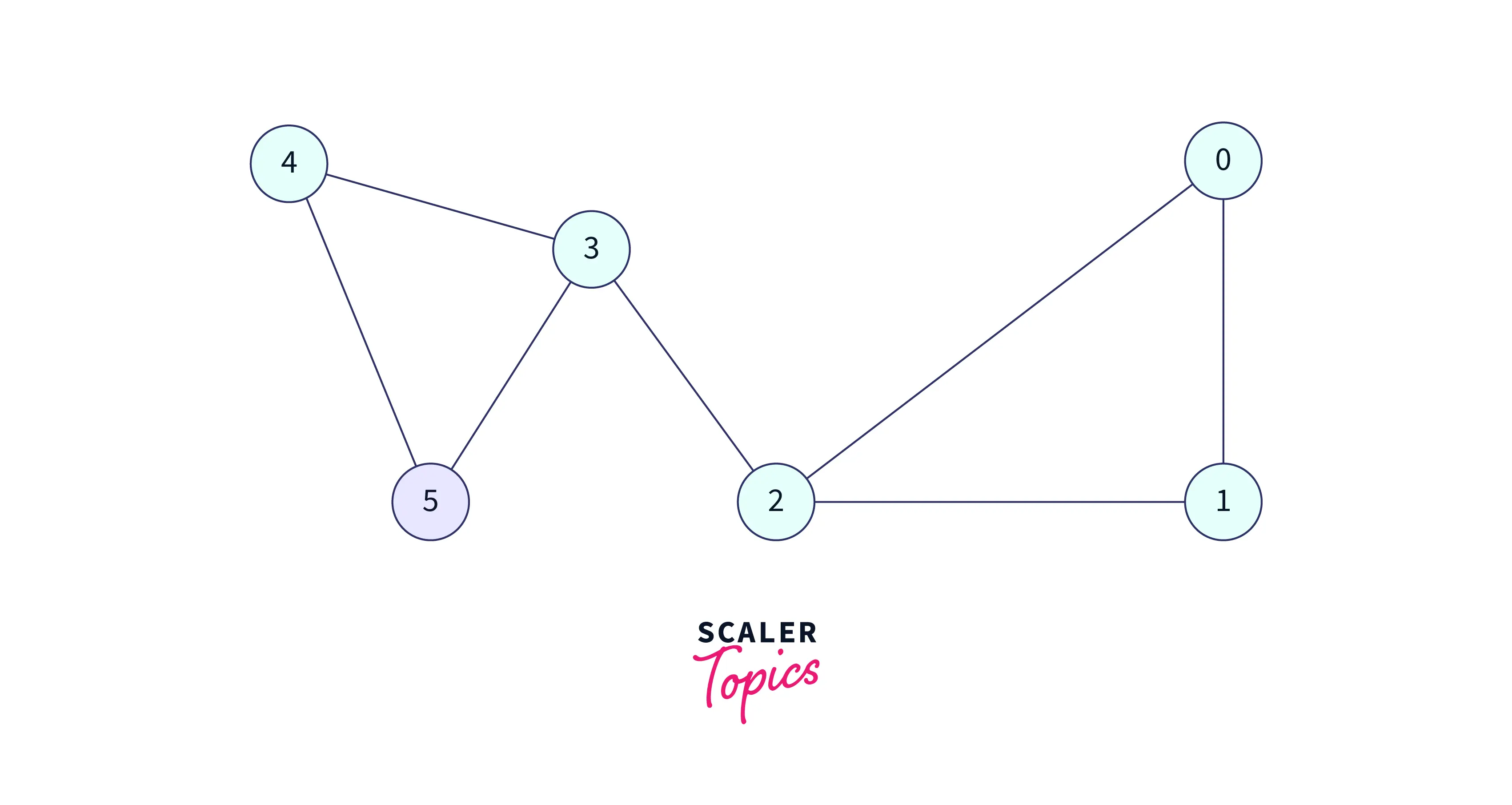
We have 2 adjacent nodes to 5, in which 3 is already visited so we have to select the only option which is 4, let's visit the 4. Visit 4 and add this to the DFS traversal,

adding-node-4-to-dfs-traversal

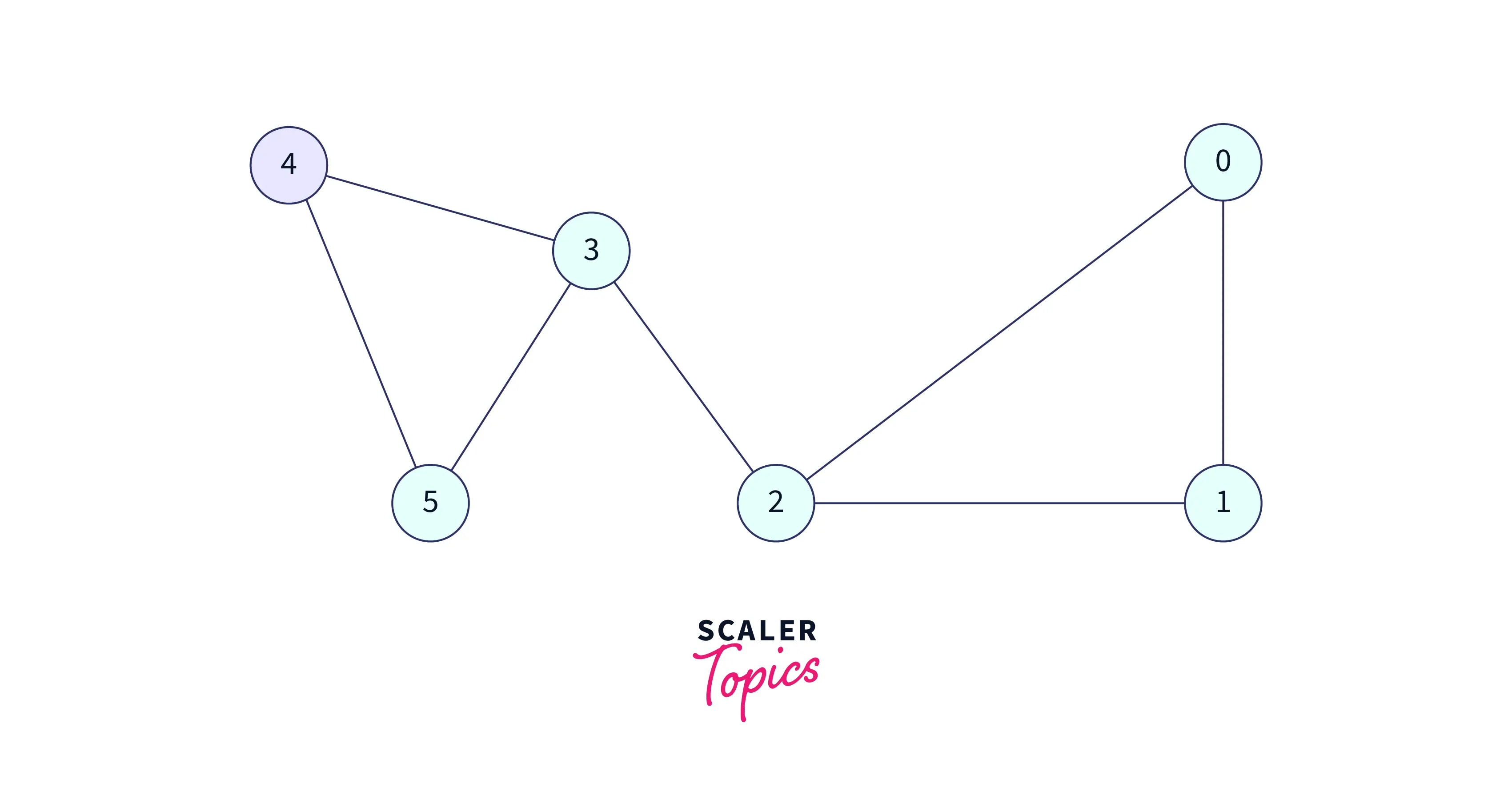
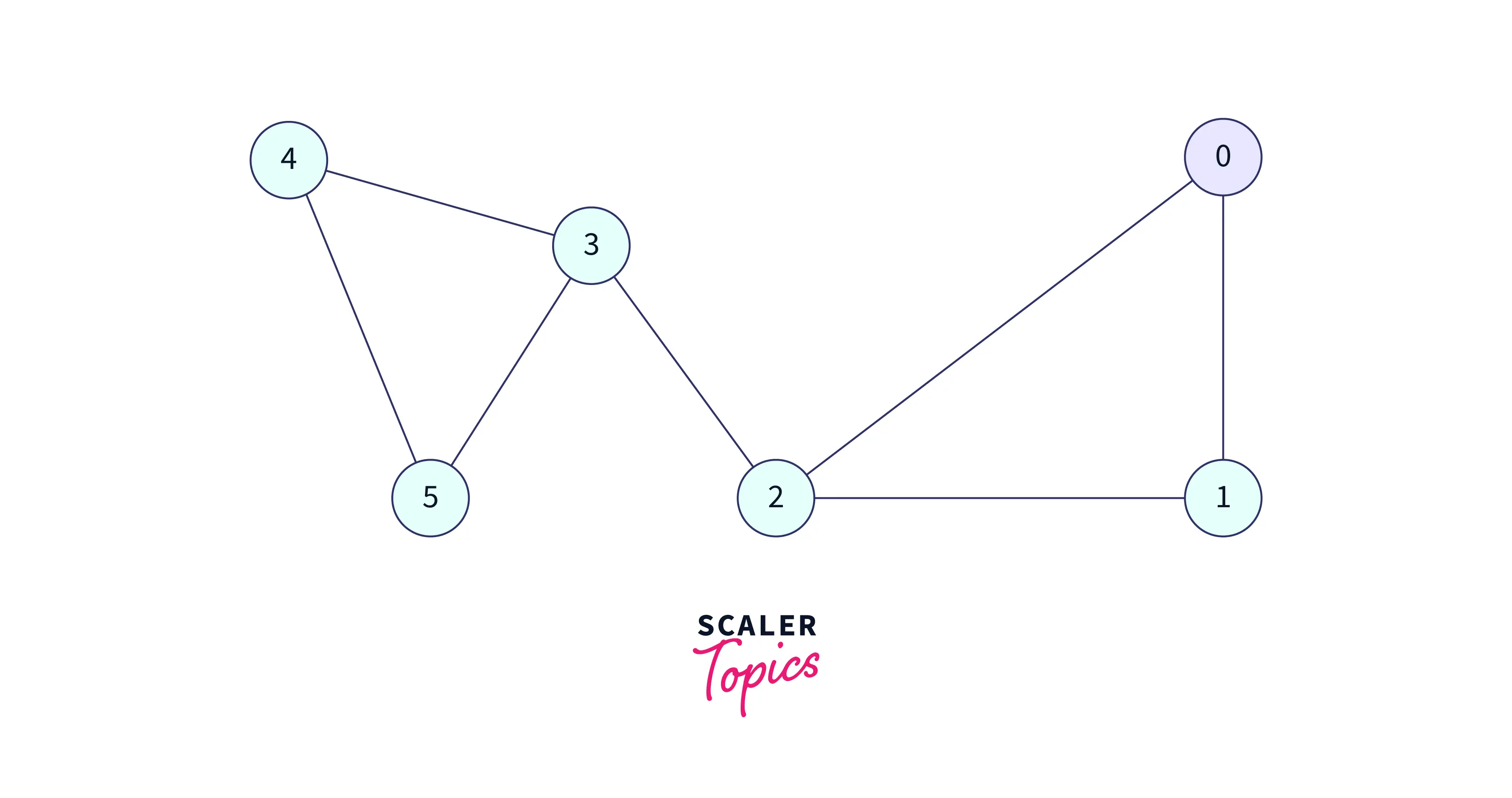
Now all adjacent to 4 has been visited so return to 5, again all adjacent to 5 have been visited so return to 3, also all adjacent to 3 have been visited so return to 2. Now, we have two options to visit 1 or 0. Let's visit 0.

Visit 0 and add this to the DFS traversal,

adding-node-0-to-dfs-traversal

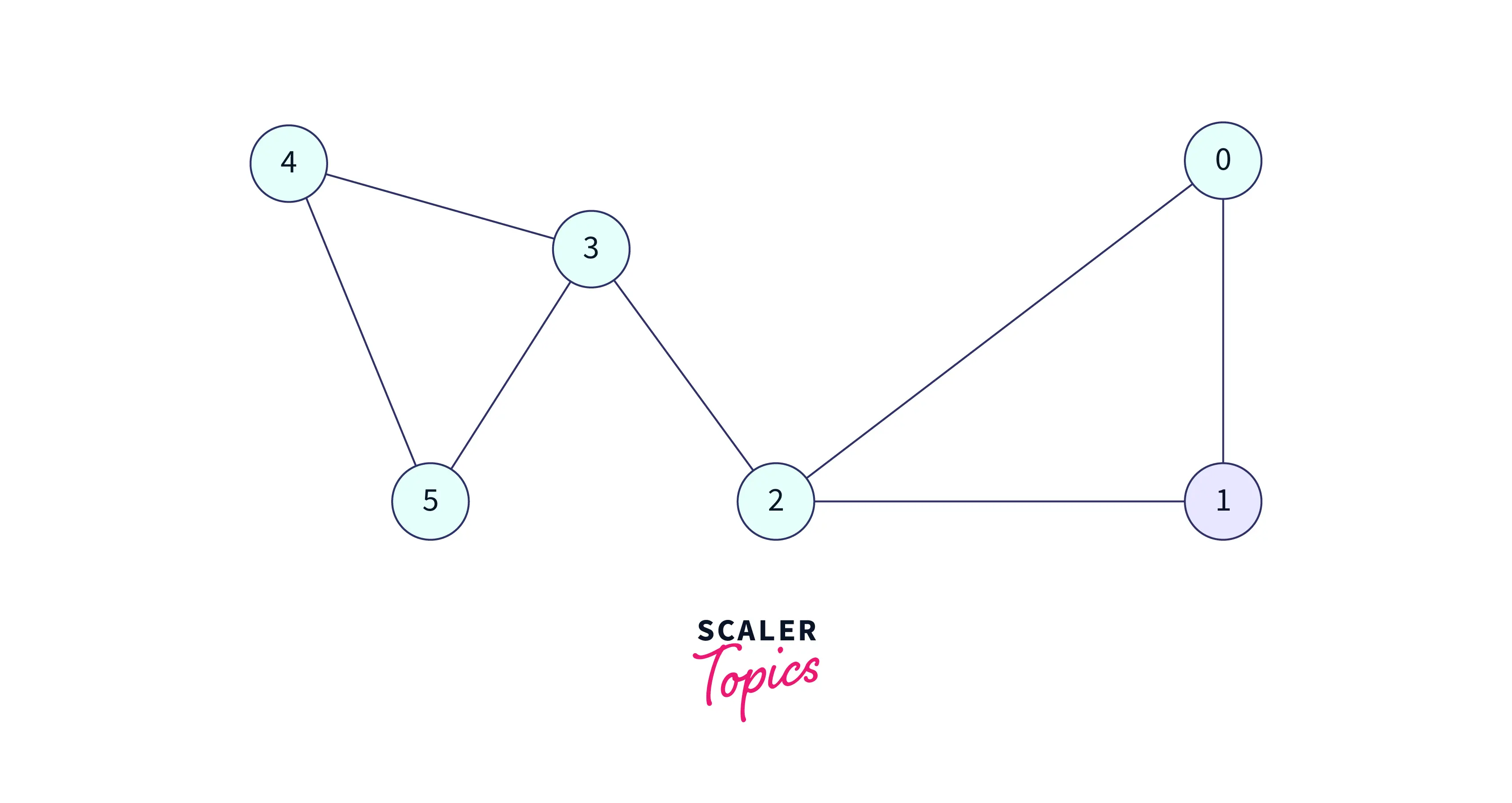
Visit 1 and add this to the DFS traversal,

adding-node-1-to-dfs-traversal

DFS Pseudocode

The pseudocode for the DFS program in C is given below,

DFS Implementation in C

In this section, we'll discuss how the DFS program is implemented in C.

Input:

Sample Input Graph:

input-dfs-implementation-in-c

Output:

Examples or Applications of DFS Program in C

DFS Traversal for Binary Trees

Depth-first search is used for traversing binary trees also, in this traversal the searching starts from the root, and a particular path is traversed till its leaf node further the algorithm returns to one parent up to discover other siblings.

A binary tree's depth-first traversal is further classified into three categories based on the occurrence of nodes.

Pre-order: when the root comes first, then the left, and then the right node/subtree.
- ROOT | LEFT | RIGHT
In-order: When the root appears before the right node but after the left node/subtree.
- LEFT | ROOT | RIGHT
Post-order: When the root appears after the right node followed by the left node.
- LEFT | RIGHT | ROOT

Input:

Sample Input Tree:

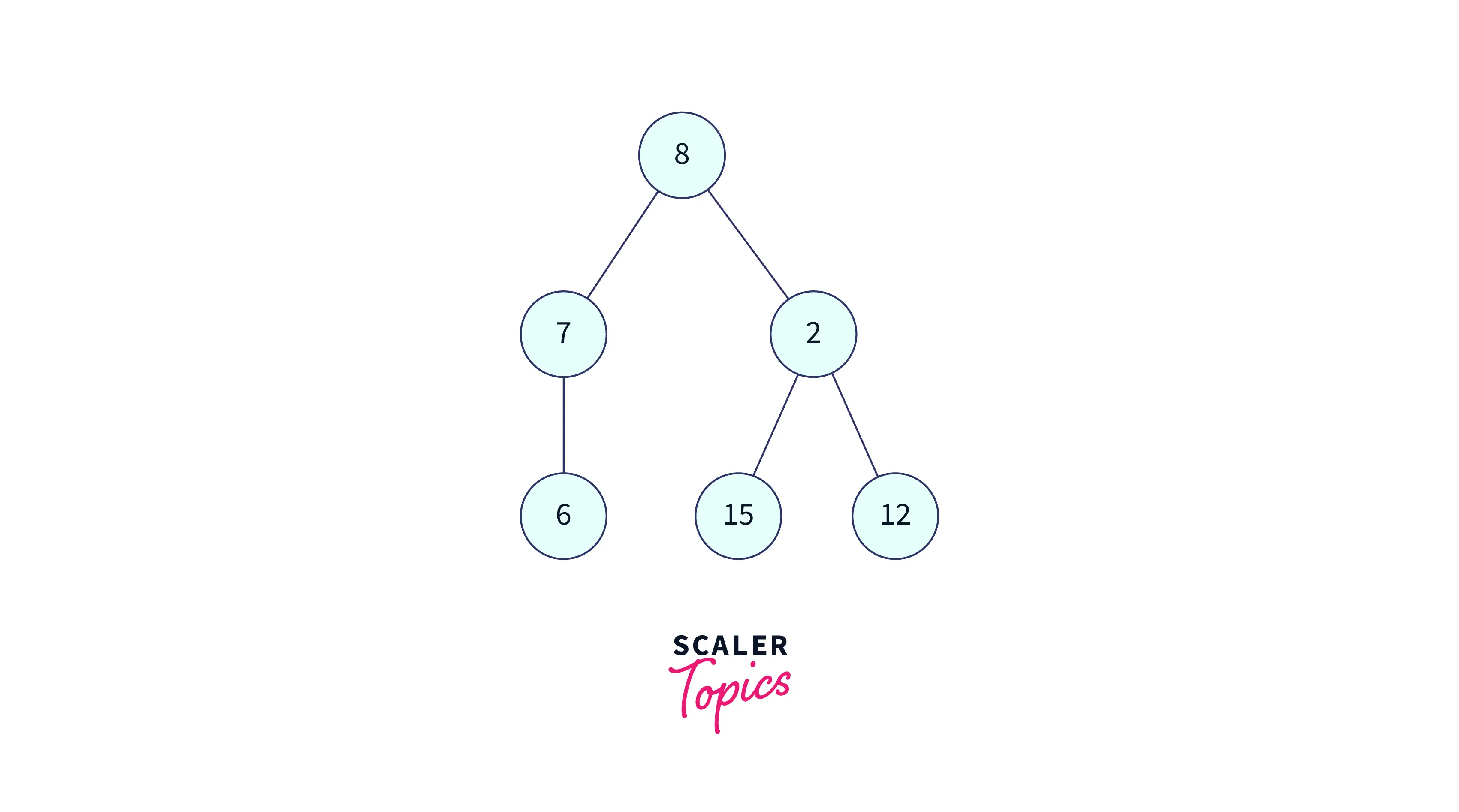
input-dfs-traversal-for-binary-trees

Output:

Find Whether a Path Between Given Vertices Exist

DFS Traversal can be used to solve the problem of determining whether a path between two vertices in a graph exists or not.

You can notice we have just manipulated the Algorithm which was earlier being used for DFS traversal for this problem statement. The solution to this problem lies in the fact that, if two vertices have a path in between them, then DFS traversal will reach another vertex if we start from one vertex, so in the algorithm, we will check whether our start and end vertices are same or not, if yes then there is a path otherwise no.

Input:

Sample Input Graph:

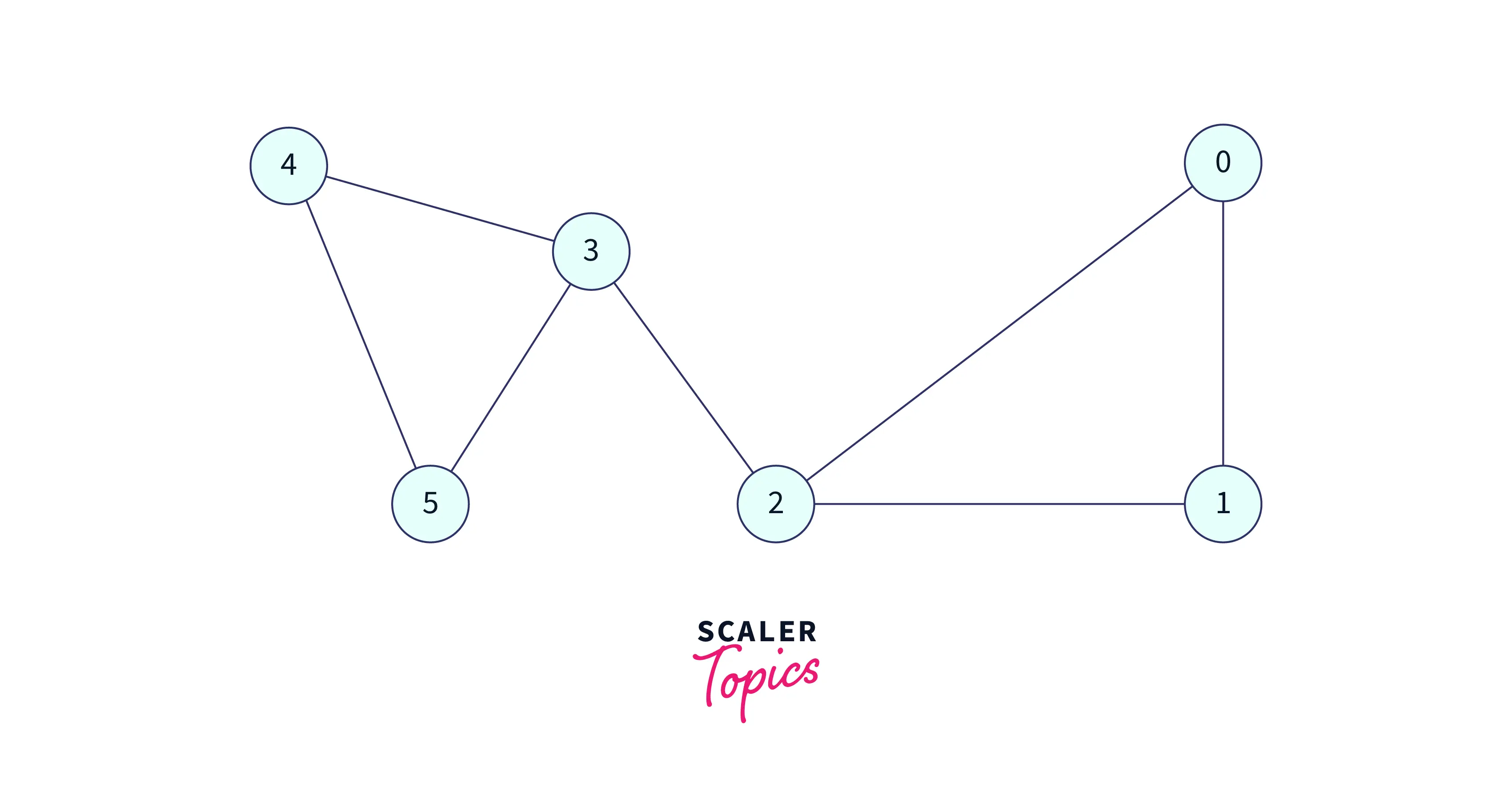
input-find-path-between-given-vertices-exist

Output:

Conclusion

To explore the entire non-linear data structure, a Standard traversal/searching technique is needed.
Depth-first Search is one of the major searching techniques which is used to traverse tree and graph data structures.
It follows the approach to find all node's descendants to the current node, which means exploring to the maximum possible depth, before proceeding to the next node.
Path finding, detecting cycles in the graph, topological sorting, and making a clone of the graph are some of the problems that can be solved with DFS.
Additionally, DFS is extensively used for Grid-Based Problems.
Recursion makes it simple to implement DFS, but iterative DFS requires the implementation of a user-defined stack to maintain the order of node exploration, which introduces overhead, and since recursion already has built-in stack assistance so it is a better option.