Difference between B Tree and B+ Tree

Introduction
The B tree is a self-balancing tree that aids in data maintenance and sorting while also allowing for searching, insertions, deletions, and sequential access. The B+ tree, on the other hand, is an extension of the B tree that aids in alleviating the inherent problems with the B tree. Let's look at some of the key distinctions between the B tree and the B+ tree.
B tree
B tree is an m-way tree that self-balances. Because of their balanced nature, such trees are widely used to organize and manage massive datasets and to facilitate searches.
Binary trees have a maximum of 2 children, whereas a Multiway Search Tree, also known as an M-way tree, has a maximum of m children where m>2. M-way trees are primarily used in external searching, i.e. retrieving data from secondary storage such as disc files, due to their structure.
Structure of B Tree
A B-tree of order m is an m-way search tree that is either empty or satisfies the following characteristics:
- All leaf nodes are at the same level.
- All non-leaf nodes (except the root node) have at least [m/2] children.
- All nodes (except the root node) should have at least [m/2]-1 keys.
- If the root node is a leaf node (only node in the tree), then it will have no children and will have at least one key. If the root is a non leaf node, then it will have at least 3 children and at least one key.
- A non leaf node with n-1 key values should have n non NULL children.
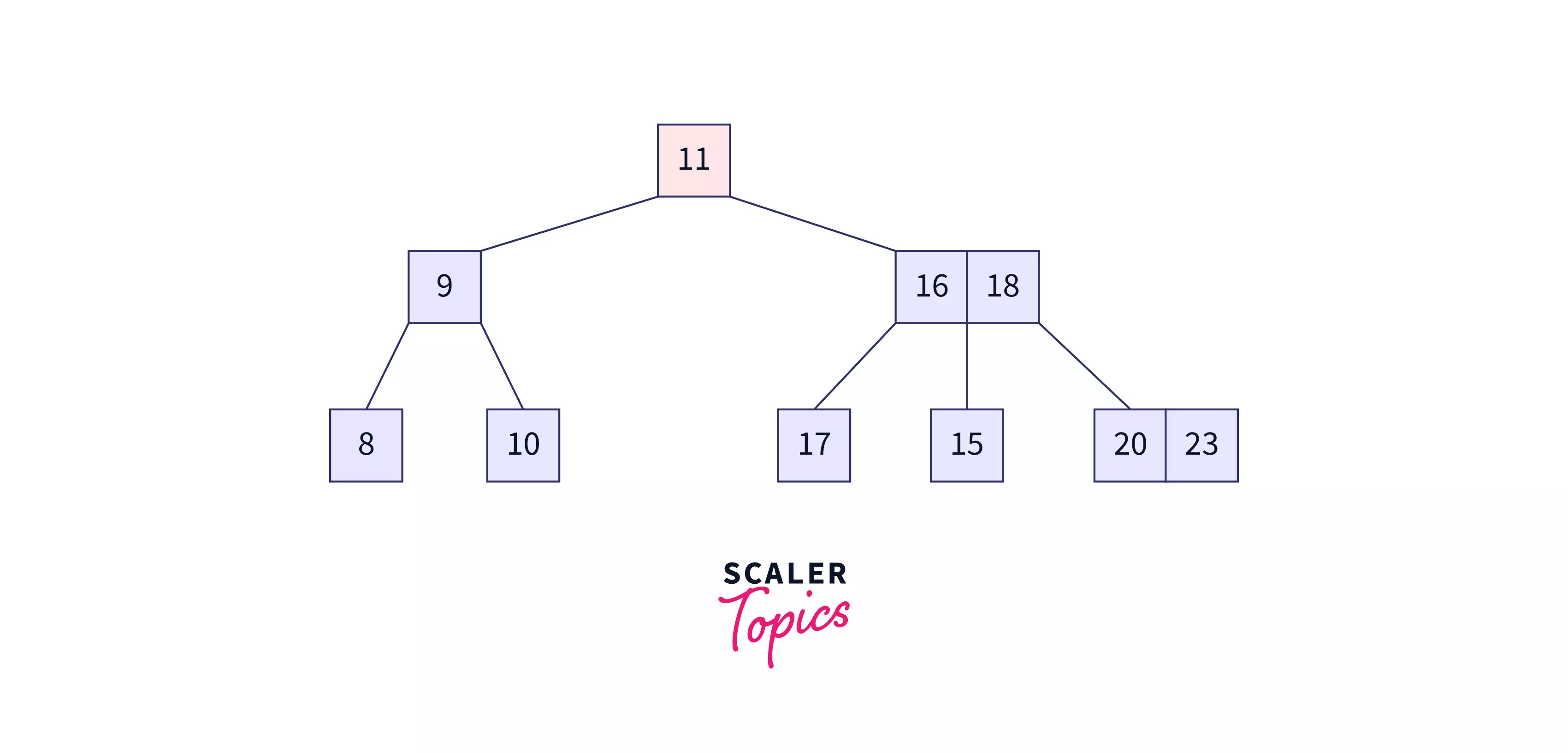
The figure above is an example of a B Tree. It has [11] at the root. 9 that is lesser than 11 falls in the left child. [16, 18] being greater than 11 a falls in the right child. The same process follows as we go down the tree.
From this, we can see that any node (except root) in a B-tree is at least half-full and this avoids wastage of storage space. The B tree is perfectly balanced so that the number of nodes accessed to find a key becomes less.
Operations on B Tree
The B tree may be split or joined to ensure that none of its properties are violated during the operations.
Searching in B Tree
The process of searching in a B Tree is similar to that of searching in a Binary Search Tree. Unlike a BST, however, instead of making a 2-way decision (left or right), a B tree makes an n-way decision at each node, where n is the node's number of children.
Following are the steps to search an element in B Tree:
- The search begins with the root node.
Contrast the root with the search element k.
- The search is complete if the root node contains the character k.
- If k is the first value in the root, we move to the leftmost child and recursively search for the child.
- If the root has only 2 children, go to the rightmost child and search the child recursively.
- If the root contains more than 2 keys, search the remainder.
- If k is not found after traversing the entire tree, the search element does not exist in the B Tree.
Insertion in B Tree
When inserting an element into the B tree, we must first check to see if the item is already existent in the tree. If the element is found, the insertion does not occur. If not, we will continue with the insertion. 2 cases must be addressed when inserting the key into the leaf node:
- Node contains no more than MAX number of keys - Simply add the key into the node in its proper location.
- Node has the maximum number of keys - A key is inserted into the full node, and then a split occurs, dividing the full node into three parts. The second or median key becomes the parent node, while the first and third parts serve as the left and right children. If the parent node also has a MAX number of keys, the process is repeated.
The following are the steps for inserting an element into B Tree:
- Determine the maximum number of keys in the node based on the B tree's order.
- If the tree is empty, a root node is allocated and the key is inserted and acts as the root node.
- Search the appropriate node for insertion.`
- If the node is full:
4.1. Insert the elements in increasing order.
4.2. If the elements are greater than the maximum number of keys, split at the median.
4.3. Push the median key upwards and split the left and right keys as left and right child respectively. - If the node is not full, insert the node in increasing order.
Deletion in B Tree
During insertion, we had to make sure that the number of keys in the node did not exceed a certain limit. Similarly, during deletion, we must ensure that the number of keys remaining in the node does not fall below the minimum number of keys that a node can hold. As a result, instead of a split, a combination process occurs in the case of deletion.
We would consider two scenarios when deleting an element from the B Tree:
- Deletion from a leaf node.
- Deletion from a non-leaf node.
Case 1 - Deletion from Leaf Node
1.1. If the node has more than MIN keys - Deleting a key does not violate any property, and thus the key can be easily deleted by shifting other node keys, if necessary.
1.2. If the node has less than MIN keys - This type of deletion violates a B tree property. If the keys in the left sibling exceed MIN, keys are borrowed from there. If the keys in the right sibling exceed MIN, keys are borrowed from there. If either of these conditions is not met, a node combination occurs with either of the siblings.
Case 2 - Deletion from Non-Leaf Node
In this case, the successor key (the smallest key in the right subtree) is copied at the location of the key to be deleted, and the successor is then deleted. This case is further simplified to Case 1, which is deletion from a leaf node.
Applications of B Tree
- Database or File System - Consider having to look up a person's information in the Yellow Pages (the directory containing details of professionals). B Tree can be used to create a system in which you need to search for a record among millions.
- Search Engines and Multilevel Indexing - B tree Searching is used in search engines as well as MySql Server querying.
- To store blocks of data - Because of its balanced structure, B Tree aids in the faster storage of blocks of data in secondary storage.
B+ tree
B+ tree is simply an improved version of the B tree that allows for efficient and smooth insertion, deletion, and sequential access. It helps to mitigate the disadvantages of the B-tree by saving data pointers at the leaf node level and simply storing key values in internal nodes.
A B+ tree, also known as an n-array tree, is a tree with a large number of children per node.
The B+ tree is also known as an advanced self-balanced tree since every path from the tree's root to its leaf is the same length. The fact that all of the leaf nodes are the same length indicates that they all occur at the same level. It is not possible for some leaf nodes to appear at the third level while others appear at the second level.
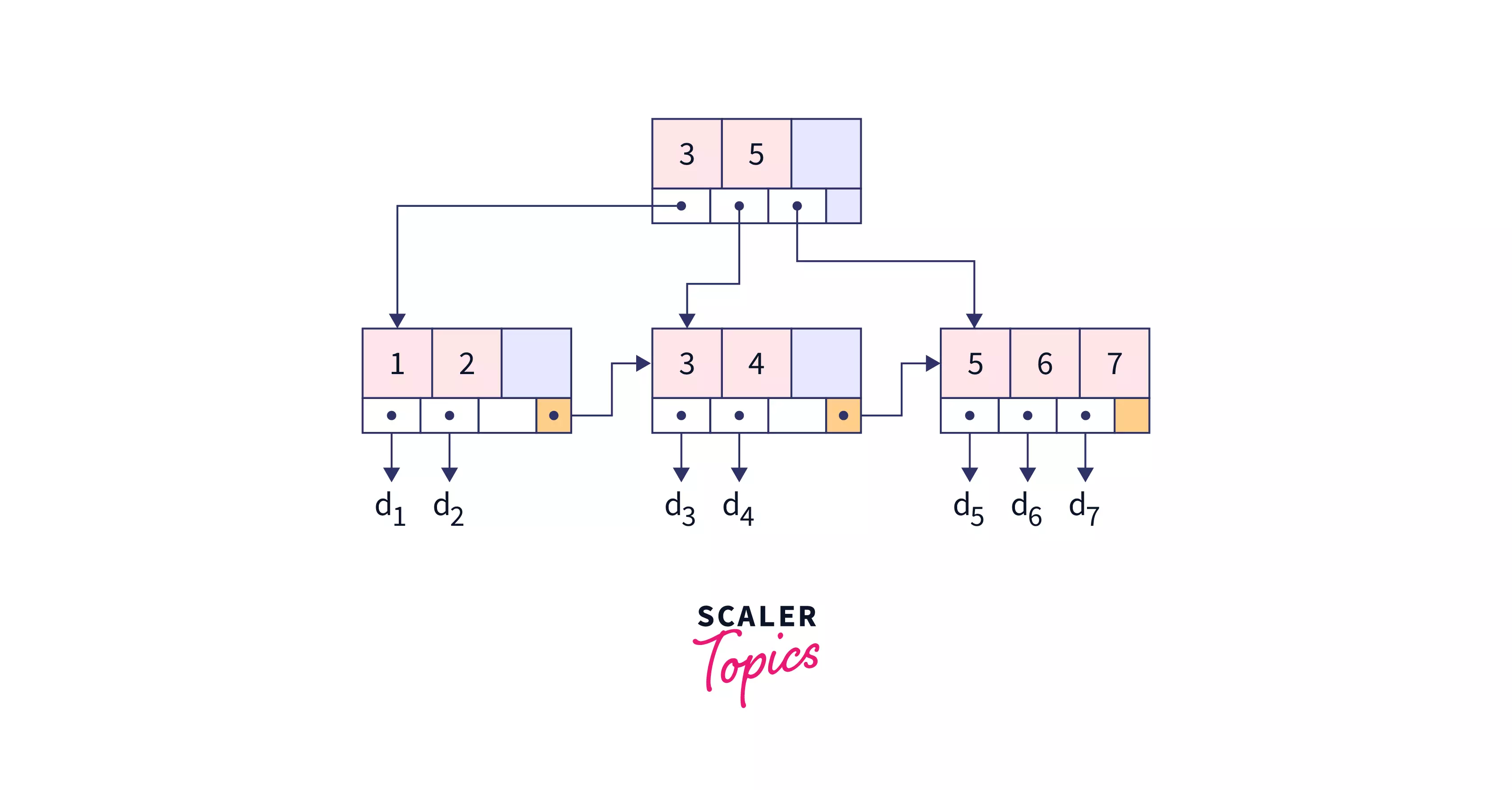
The above figure shows a representation of a B+ tree.
Structure of B+ Tree
A B+ tree is the same as a B tree; the only difference is that the B+ tree has an additional level with linked leaves at the bottom. In addition, unlike the B tree, each node in a B+ tree contains only keys rather than key-value pairs.
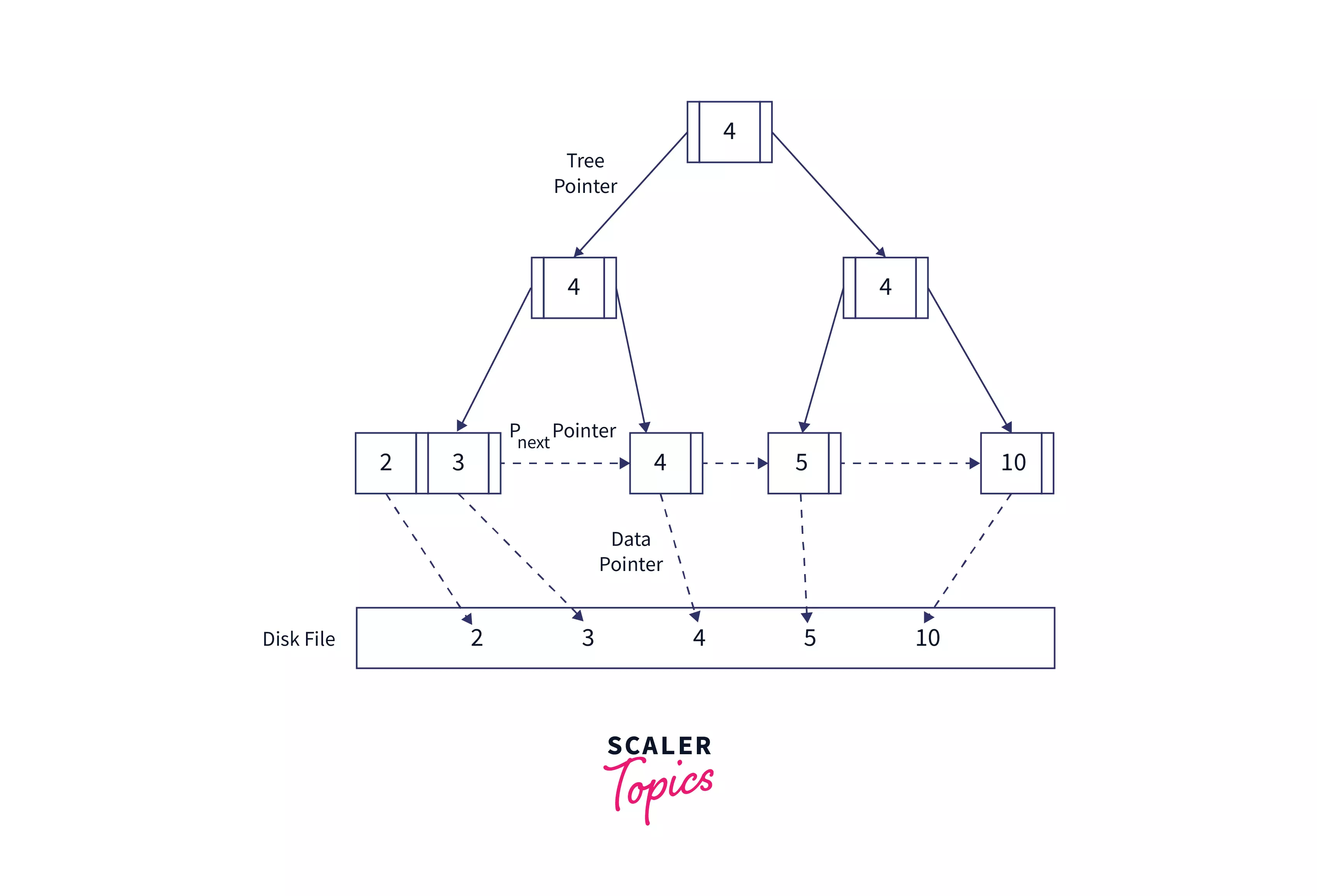
Operations of B+ Tree
Most operations in B+ Tree are faster and make up for the drawbacks of the B tree.
Searching in B+ Tree
In the B tree, our search ended when we discovered the key, but this will not be the case in the B+ tree. It is possible that a key exists in the internal node but not in the leaf node of a B+ tree. This is because when a data item is deleted from the leaf node, the corresponding key is not deleted from the internal node. The search will take place only within the leaf nodes.
Insertion in B+ Tree
First, a search is performed, and if the key is not found in the leaf node, we can have one of two outcomes, depending on whether the leaf node has the maximum number of keys or not:
- If the leaf node has fewer than the maximum number of keys, key and data are simply inserted in an ordered manner into the leaf node, and the index set is not changed.
- If the leaf node has the maximum number of keys, we will have to split it. After the old node, a new leaf node is allocated and inserted into the sequence set (linked list of leaf nodes). All keys less than the median key remain in the old leaf node, while all keys greater than or equal to the median key are moved to the new node, along with the corresponding data items. The median key becomes the new node's first key, and this key (without a data item) is copied (rather than moved) to the parent node, which is an internal node. As a result, this median key is present both in the leaf node and in the internal node which is the parent of the leaf node.
Splitting of a leaf node Keys < Median remains in the old leaf node Keys >= Median go to a new leaf node The median key is copied to the parent node
If after splitting of the leaf node, the parent becomes full then again a split has to be done. The splitting of an internal node is similar to that of the splitting of a node in a B Tree. When an internal node is split the median key is moved to the parent node.
Splitting of an internal node Keys < Median remains in the old leaf node. Keys < Median go to a new leaf node. The median key is moved to the parent node.
This splitting continues till we get a nonfull parent node. If the root node is split then a new root node has to be allocated.
Deletion in B+ Tree
First, a search is performed, and if the key is not found in the leaf node, we can have one of two outcomes, depending on whether the leaf node has the minimum number of keys or not:
- If the leaf node has more than minimum elements, then we can simply delete the key and its data item, and move other elements of the leaf node if required. In this case, the index set is not changed, i.e. if the key is present in any internal node also then it is not deleted from there. This is because the key still serves as a separator key between its left and right children.
- If the leaf node has a minimum number of nodes:
2.1. If any of the siblings have more than minimum nodes, then a key is borrowed from it and the separator key in the parent node is updated accordingly.
2.2. If both siblings have minimum nodes then we merge the underflow node with its sibling. This is done by moving keys and data from the underflow node to the sibling node and deleting the underflow node. The merging could result in an underflow parent node which is an internal node. For the internal nodes, the borrowing and merging process is similar to that of the B tree.
Applications of B+ Tree
- A B+ tree is used to store records very efficiently by indexing the records using the B+ tree indexed structure. Data access becomes faster and easier as a result of multi-level indexing.
- A B+ tree's structural simplicity is preferred by many database system implementers. As a result, it is commonly used in multilevel and database indexing.
Summary
| S No. | B Tree | B+ Tree |
|---|---|---|
| 1 | All keys and records in the B tree are stored in both internal and leaf nodes. | The keys in the B+ tree are the indexes stored in the internal nodes, while the records are stored in the leaf nodes. |
| 2 | Keys in the B tree cannot be stored repeatedly, so there is no key or record duplication. | The occurrence of the keys in the B+ tree may be redundant. In this case, the records are stored in the leaf nodes, while the keys are stored in the internal nodes, which means that redundant keys may exist in the internal nodes. |
| 3 | Leaf nodes in the B tree are not connected to one another. | The leaf nodes in a B+ tree are linked to each other to provide sequential access. |
| 4 | Searching in a B tree is inefficient because records are stored in either leaf or internal nodes. | Because all records are stored in the leaf nodes of the B+ tree, searching is very efficient or faster. |
| 5 | Insertion takes longer and can be unpredictable at times. | Insertion is simpler, and the results are consistent. |
| 6 | Internal node deletion is a slow and time-consuming process because we must consider the deleted key's child as well. | Because all records are stored in the leaf, deletion in the B+ tree is very fast. |
| 7 | Sequential access is not possible in the B tree. | All of the leaf nodes in the B+ tree are linked to each other via a pointer, allowing for sequential access. |
| 8 | The greater the number of splitting operations performed in a B tree, the greater the height relative to width. | The width of a B+ tree is greater than its height. |
| 9 | Because each node in the B tree has at least two branches and each node contains some records, we don't need to traverse to the leaf nodes to get the data. | Internal nodes in a B+ tree contain only pointers, whereas leaf nodes contain records. Because all of the leaf nodes are at the same level, we must traverse until we reach the leaf nodes to obtain the data. |
| 10 | The structurally linked list does not store leaf nodes. | Leaf nodes are stored in the form of a structurally linked list. |
