How to Find the Factorial of a Number in JavaScript?

The factorial of a number in mathematics is used to find out the number of ways things can be arranged. The factorial function was discovered by Daniel Bernoulli. In simple terms, we can say that the factorial of a number is just the product of all the numbers from 1 to the current number.

Factorial of a number in JavaScript is a function that multiplies a number by every number below the number to 1. The factorial of a number is one of the most important mathematical concepts that is used in various other concepts such as permutations and combinations, sequences and series, etc.

Let us take an example to understand the factorial of a number. Suppose we want to find the factorial of $6$. The factorial of $6$ represents the multiplication of numbers 6, 5, 4, 3, 2, 1. i.e., $6!$ = $(6 * 5 * 4 * 3 * 2 * 1)$, which comes out to be $720$.

Factorial Formula

The formula to find the factorial of a number (n) is:

$n! = n × (n-1) × (n-2) × (n-3) × ... × 3 × 2 × 1$

The above recurrence relation for the factorial of a number can be summed up as the product of the factorial number and the factorial of that number minus 1. i.e., $n! = n × (n-1) !$

We can also represent the factorial of a number in terms of pi product notation as:

Syntax

The basic syntax of function declaration of the factorial program in javascript can be:

Syntax:

Here, we are providing the number (as an argument to the function) whose factorial is to be calculated.

We can call the function:

Examples

Example 1

Let us now try to implement the iterative approach of writing a factorial program in JavaScript.

Output:

We can visualize the function's iteration with the varying values of i as:

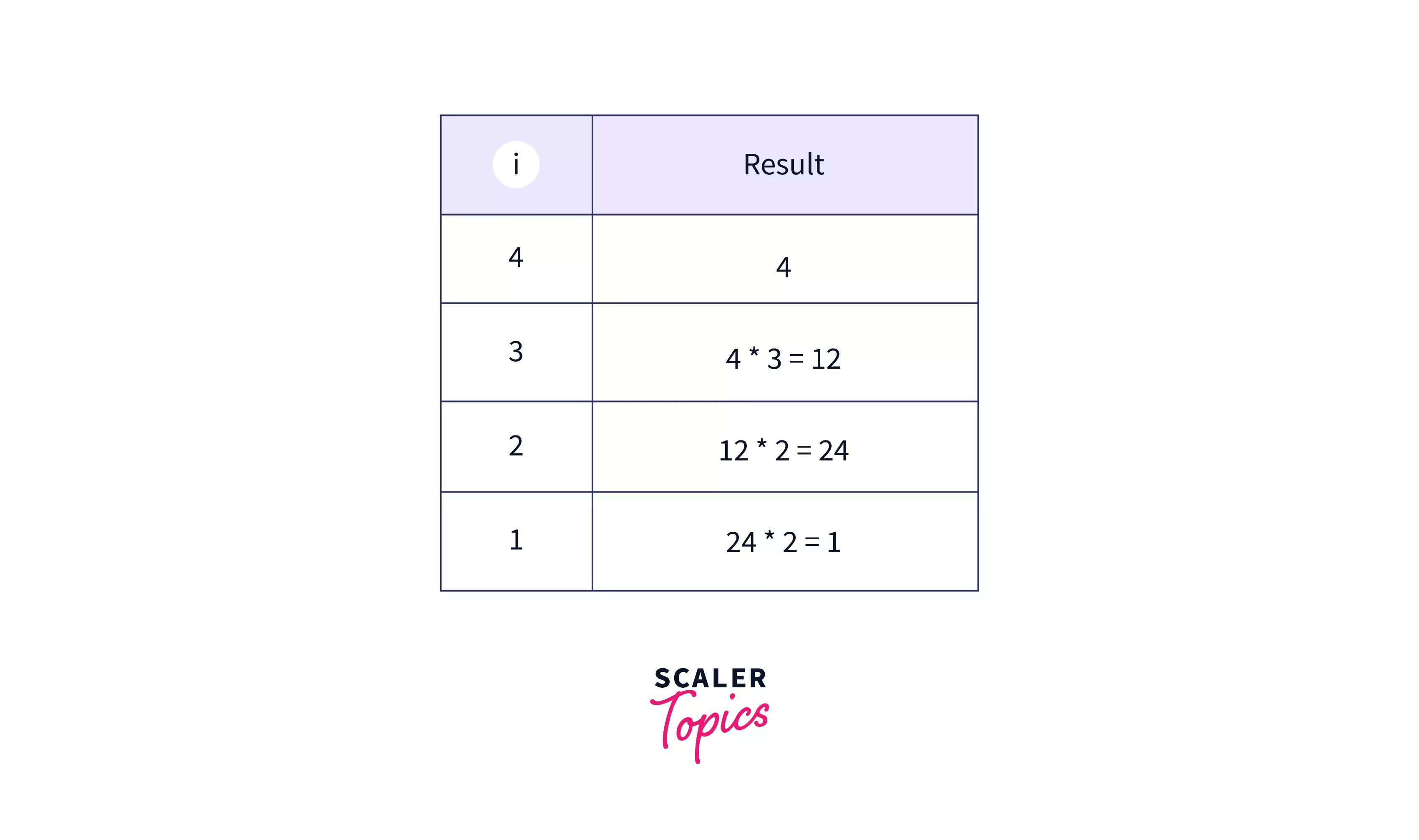
Example 2

Let us now try to implement the recursive approach of writing a factorial program in JavaScript.

Output:

We can visualize the function calls with the varying values of n as:

Approaches

Before learning about the iterative and recursive approach to writing factorial programs in JavaScript, let us first briefly discuss what iteration and recursion are.

Iteration is a process in which a set of instructions or structures are repeated in a sequence a specified number of times. In some other cases, the iteration is repeated in a sequence or until a condition is met. When a sequence of instructions is executed sequentially or repeatedly, it is called a loop.

Recursion is a widely used technique in computer science used to solve complex problems by breaking the problem into simpler ones. Recursion is a process in which a function calls itself directly or indirectly. The corresponding function is called a recursive function.

A. Iterative Method

Let us now discuss the iterative approach of writing a factorial program in JavaScript. We can maintain a variable (let's say i) that is initially set to n (provided by the user) and is gradually decremented to 1. In each iteration or step, the result of the product or multiplication is stored in the result variable. At the end of the entire iteration, the result is returned by the program, which can be further printed using console.log().

B. Recursive Method

As we have seen in the recurrence formula of finding the factorial program in javascript ($n! = n × (n-1) !$ ), the factorial of the number n can be found by simply finding the factorial of a number one less than n (i.e., n-1) and then multiplying the answer with n itself.

We can visualize that the major problem of finding the factorial of a number n can be broken down into a subproblem (factorial of (n - 1) * n). So, we need to compute the result of the subproblem first. Similarly, we will decrement the value of n till n becomes 1.

As we know, the factorial of 1 or 0 is 1 itself, so in the factorial(1) function call where n becomes 1 (i.e., n == 1 or n == 0) will act as base case of the recursive function.

One of the major benefits of using the recursive approach to writing a factorial program in javascript is that the code is much shorter and cleaner as compared to the iterative approach of writing a factorial program in javascript.