Factorial Using Recursion in Java- Scaler Topics

The factorial of a number n represents the product of all descending positive integers up to n, denoted as n! . For instance, ( 5! = 1 × 2 × 3 × 4 × 5 = 120 ). There are Various methods exist for calculating factorial, while this article will focusing on employing Java's recursive approach.

How to Find Factorial Program in Java Using Recursion?

The definition of recursion is to call the function within itself. We can use this property and calculate the factorial of the number. Let us understand the process of finding factorial using recursion by an example.

Consider a number 5, now calculate the factorial of 5. In simple terms, we can write the factorial of 5 is the product of 5 and the factorial of $4 (5! = 4! × 5)$ . Similarly, we can write:

$4! = 3! × 4$

$3! = 2! × 3$

$2! = 1! × 2$

And, the factorial of 1 is 1.

To find the factorial of a number 5 we can call a recursive function and pass the number 5 within the factorial function.
We will make a recursive call for calculating the factorial of number 4 until the number becomes 0, after the factorial of 4 is calculated we will simply return the value of $5 × 4!$ .
To calculate the factorial of 4 we will again call the recursive function. This process will continue until the number reaches 0.
So, when the number reaches zero we will simply return 1 as the factorial of 0 is 1. The following pseudo-code will help you to understand the process of calculating the factorial.

Pseudo-Code

Let us implement the above pseudo-code in Java to find the factorial of any number N.

Code

Output

Transform Your Career

Choose from our industry-leading programs designed for career success

NSDC Certified

Modern Software and AI Engineering Program

Master full-stack development with AI integration

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Modern Data Science and ML with specialisation in AI

Advanced data science techniques with AI specialization

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Advanced AIML with Specialisation in Agentic AI

Deep dive into AIML with focus on Agentic systems

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

DevOps, Cloud & AI Platform Engineering

Build and manage AI-powered cloud infrastructure

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

AI Engineering Advanced Certification by IIT-Roorkee

Premier AI engineering certification from IIT-Roorkee

3 MonthsDuration

AI-LedCurriculum

Career SupportSupport

Go to Program

Time and Space Complexity

The time complexity of the above code is $O(N)$ because we call the recursive function N times. The space complexity of the above code is again $O(N)$ because the recursion stack takes $O(N)$ space in the internal memory.

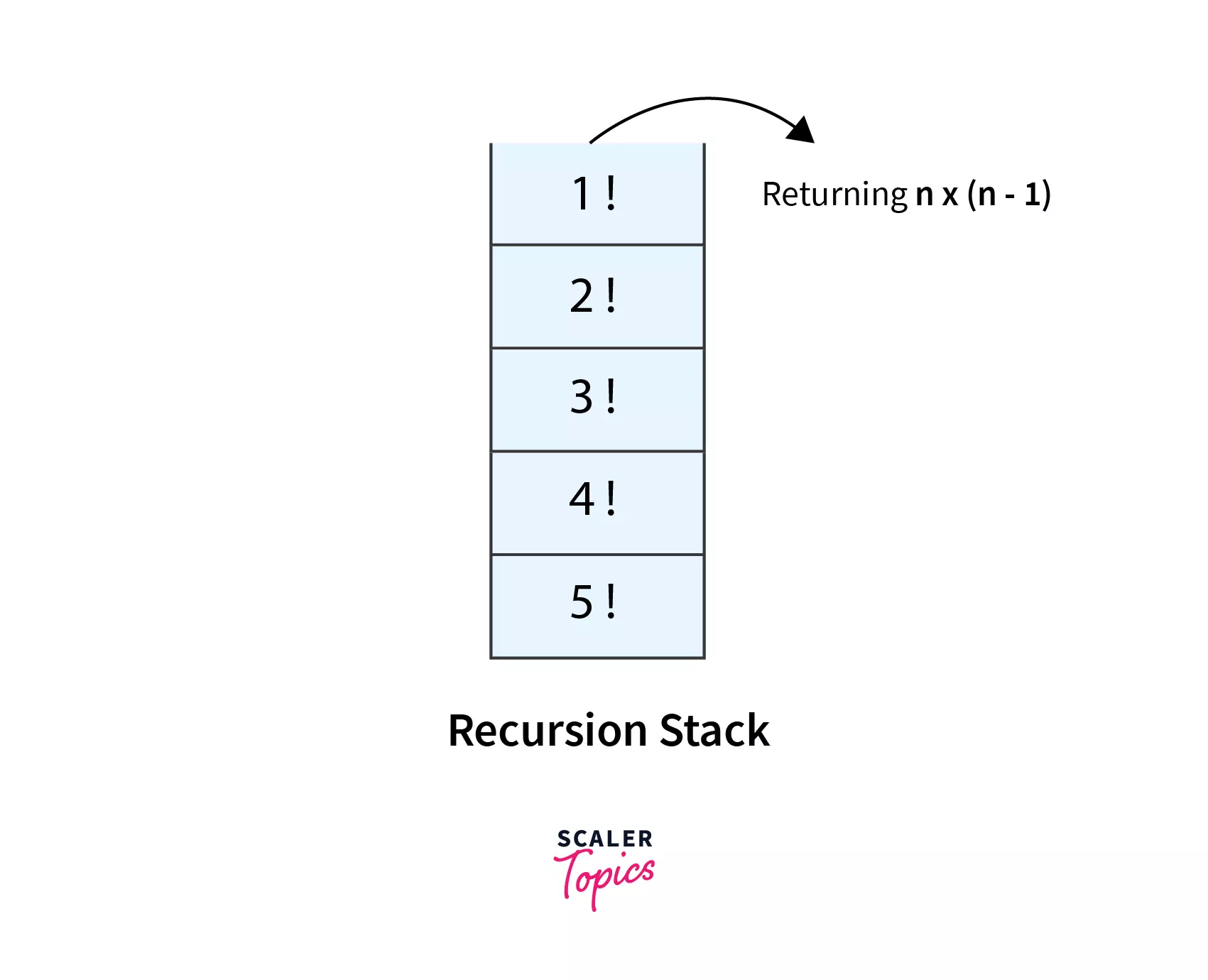
As soon as we call the recursive function, the function call occupies space on the top of the call stack. The successive calls of the function within itself consecutively acquire space on top of each other in the call stack. We can understand the call stack by the following image. recursion stack

When the method factorial() is called with argument equal to 0, the method returns the value 1, post which all the methods return the required values and get popped out from the call stack.

Iterative Method

In the iterative method:

We will declare a variable res and initialize its value to 1.
Now run a for loop from 1 to N. Every time we iterate in the loop multiply the res variable with the counter of the loop.
Finally, after the execution of the loop result will be stored in the res variable.

Code

Output

Turn Learning into Career Growth

1200+Hiring Partners

89%Placement Rate

11,000+Placements

147%Avg Salary Increment

2.5XCareer Growth

₹23 LPAAvg Post-Scaler Salary

1200+Hiring Partners

89%Placement Rate

11,000+Placements

147%Avg Salary Increment

2.5XCareer Growth

₹23 LPAAvg Post-Scaler Salary

Comparing Linear and Recursive Methods

Let us differentiate between the recursive and iterative method based on time and space complexities.

Comparing the time complexity of both methods we can say that both iterative and recursive methods take $O(N)$ time.

Difference lies in the space complexity

In terms of space complexity, the iterative method takes $O(1)$ space which is constant space whereas the recursive method takes $O(N)$ memory space. This is due to the $O(N)$ recursive method calls which acquire space order N space in the call stack.

Conclusion

Recursion breaks a problem into smaller sized problems and finds the solutions to these subproblems. Using the solutions to these subproblems it builds up the solution to the larger problem.
The time and space complexities of the recursive method are both equal to $O(N)$ where we need to find the factorial of number N.
The time and space complexities of the iterative method are $O(N)$ and $O(1)$ respectively.
Calculating factorial using recursion is a space-consuming process as compared to the linear method. When the number N grows large, it is not possible to compute N! using the recursive method.
Implementing recursive codes helps in many types of problems like Depth First Search, Breadth-First Search, Tree Traversal techniques where the linear method won’t work.