Factors of a Number in Python

Factors of a Number in Python

A factor of a number 'n' is the one that divides the number 'n' completely, that is, on dividing 'n' with it, the remainder should be zero.

For Example -

The output contains all the numbers that would give a remainder 0 when divided by 24.

We have a lot of numbers such as Prime numbers, composite numbers, etc. in our Number system.

The numbers that have only two factors, 1 and itself are called Prime numbers whereas the numbers that have more than two factors are known as composite numbers.

However, factorization of a number can be defined as breaking the number into a product of smaller numbers which when multiplied together will give the original number.

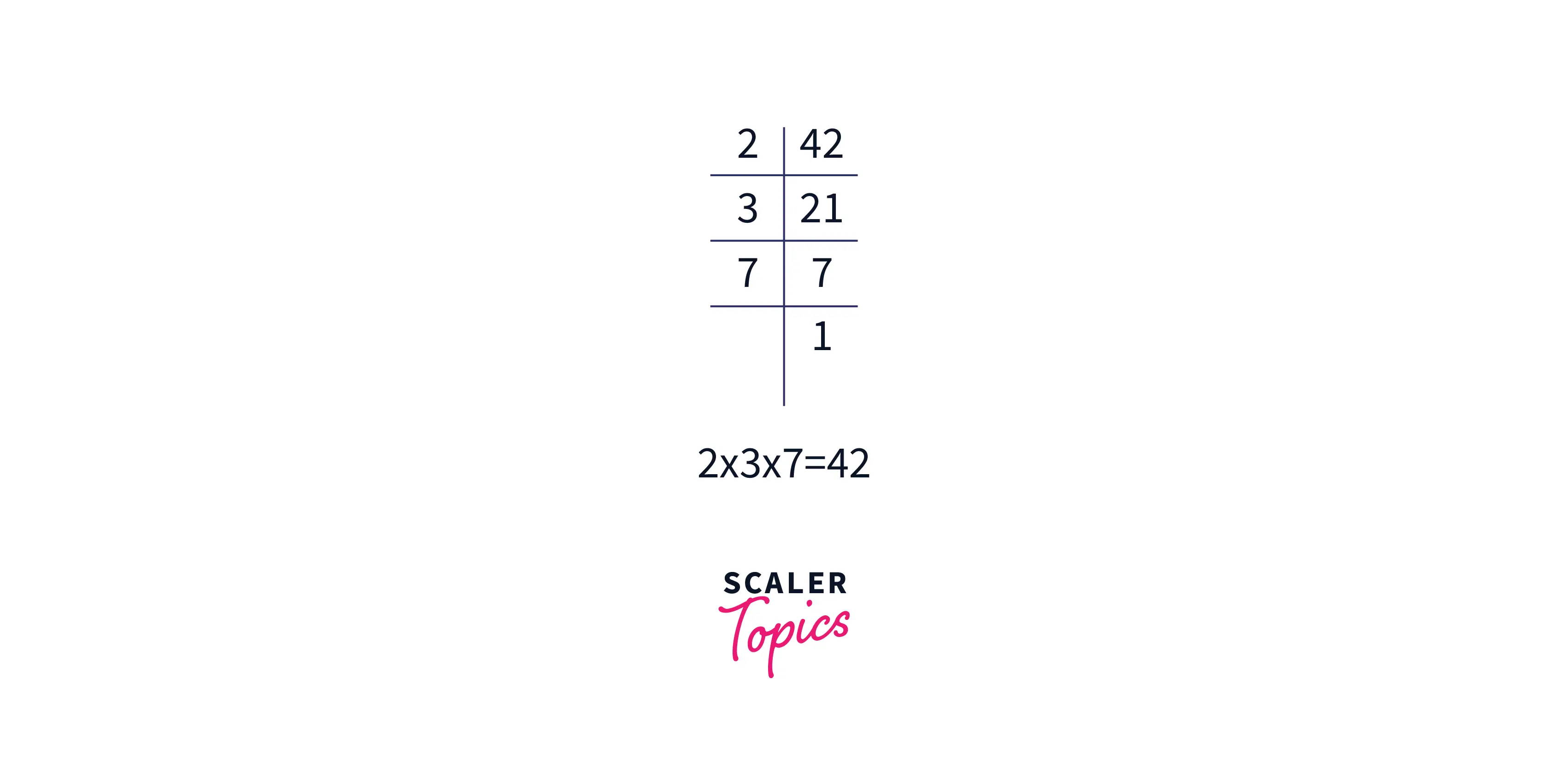
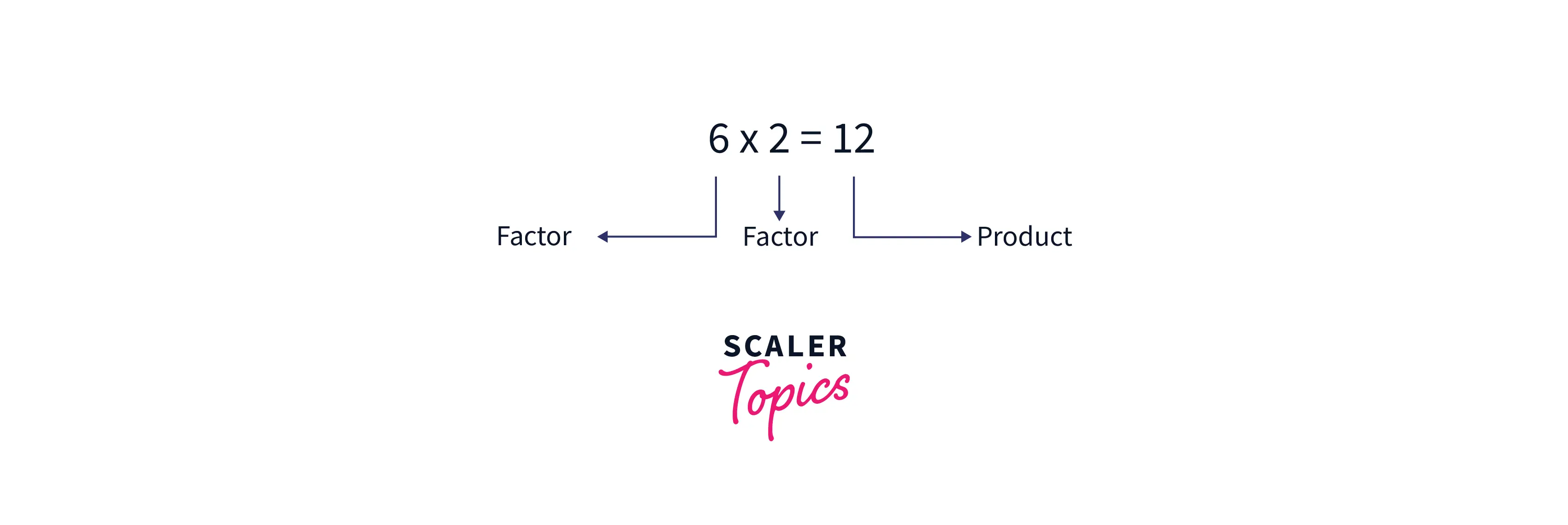
On the other hand, if on multiplying two numbers we get their product then the numbers that were multiplied will be factors of the product because they both leave a remainder zero on dividing with the product.

Python Program to Find the Factors of a Number

Finding Factors of a Number Using for Loop

Now, let us see the program to find the factors of a number in Python using for loop. It is one of the easiest ways to find the factors of a number. In this approach, we check for each number from 1 to N if it divides N, if yes then we print it.

The code is as given below -

Output:

In the above program, we are just iterating from 1 to the number itself and checking if each number in this range is completely divisible by the given value of 'N'. If it leaves a remainder of 0 then we print the result otherwise check for another value in the range.

The print statement includes the end keyword as end=' ' which is just used to print the numbers in the same line.

The time complexity of the above solution will be an order of N since we are using only one loop to solve our problem. However, the space complexity will be constant as we are not using any extra space to find the factors of a number.

Finding factors of a number using a while loop

The factors of a number can be found using the while loop. However, the logic is similar to the for loop, only the syntax is what has changed.

Let us see it in detail.

Output:

The factors of a number can only be present up to that number. Therefore, we are checking the condition up to less than equal to N. If the number x is divisible by N, therefore, it is a factor of N and hence it is printed.

Since we are traversing through the while loop only once, therefore, it has a time complexity of the order of N and since we are not using any extra space, so the space complexity of the above solution is constant.

Time Complexity: O(N)
Space Complexity: O(1)

An Optimized approach for finding the factors of a number

In this approach, we will be talking about a more optimized solution than the other two that we have previously talked about. It is an optimized solution because previously we were traversing the loop till the number itself but now we are traversing only till half of N, more precisely till the square root of N. Therefore, its complexity will be reduced and it will work faster than the other two.

In this approach, a very important observation after finding the factors is that all the factors exist in pairs.
Let's explain it with an example.

As we can see $(1x24$, $(2x12)$, $(3x8)$, $(4x6)$, all when individually multiplied give us 24. Moreover, all these numbers individually are also the factors of N.

Therefore, using this observation, we can run a loop that will go only to half of N, that is, the square root of N because after that the values will start repeating themselves.

Let us see the code for a better understanding.

In the first line, we are importing the math module inside our program that allows us to use the sqrt() function present in it.

We are then defining a function printFactors which has our main logic to print the factors of a number. Inside the function, we are initializing the variable x which will be increased in every iteration so that every number between 1 to Math.sqrt(N) would be checked for its divisibility with N.

However, we are running a loop only till sqrt(N) because after that the pairs will start repeating themselves.

For example, N=16

The pairs will be $(1x16)$, $(2x8)$, $(4x4)$, $(8x2)$, $(16x1)$.

Since $sqrt(16) = 4$ and as you can see after 4, the pairs have started repeating themselves as $(2x8)$ is the same as $(8x2)$ and $(1x16)$ is the same as $(16x1)$. Therefore, to avoid this we are taking the loop till sqrt(N).

Inside our while loop, we are checking for the divisibility of N with x, which if true, tries to find its pair by N/x.

However, there are two conditions written inside our if condition. The first condition is checked for avoiding the repetition of a number and the second condition is for actually printing the pairs.

These are factors that will be printed when the repetition condition is not taken into account.

The value 4 is repeating itself, but we do not want repetition in our output. Therefore, the if condition if(N/x==x) is used to avoid such situations.

Time Complexity: O(sqrt(N))
Space Complexity: O(1)

Prime Factors of a Number in Python

Prime numbers are the numbers that are divisible by only 1 and themselves. Similarly, prime factors are prime numbers that are also a factor of a number.

For example, N=6

The factors of 6 are 1, 2, 3, 6 where 2,3 are prime numbers as well as the factors therefore, 2,3 are the prime factors of 6.

However, we will be calculating these factors by the prime factorization method. Prime Factorisation is the method in which we recursively divide the number with its prime factors to find all the prime factors of the number.

Let us see the program for the same.

In the above, after taking the input, we run a loop from 2 because prime numbers start from 2 and end our loop at math.sqrt(N)+1 as the factors will not be present after reaching half of N.

Now, we keep on dividing the value of N until possible with i to find its prime factors and simultaneously print them.

However, there would be a case left where we need to apply an extra condition for $N!=1$.

For example, $N=46$

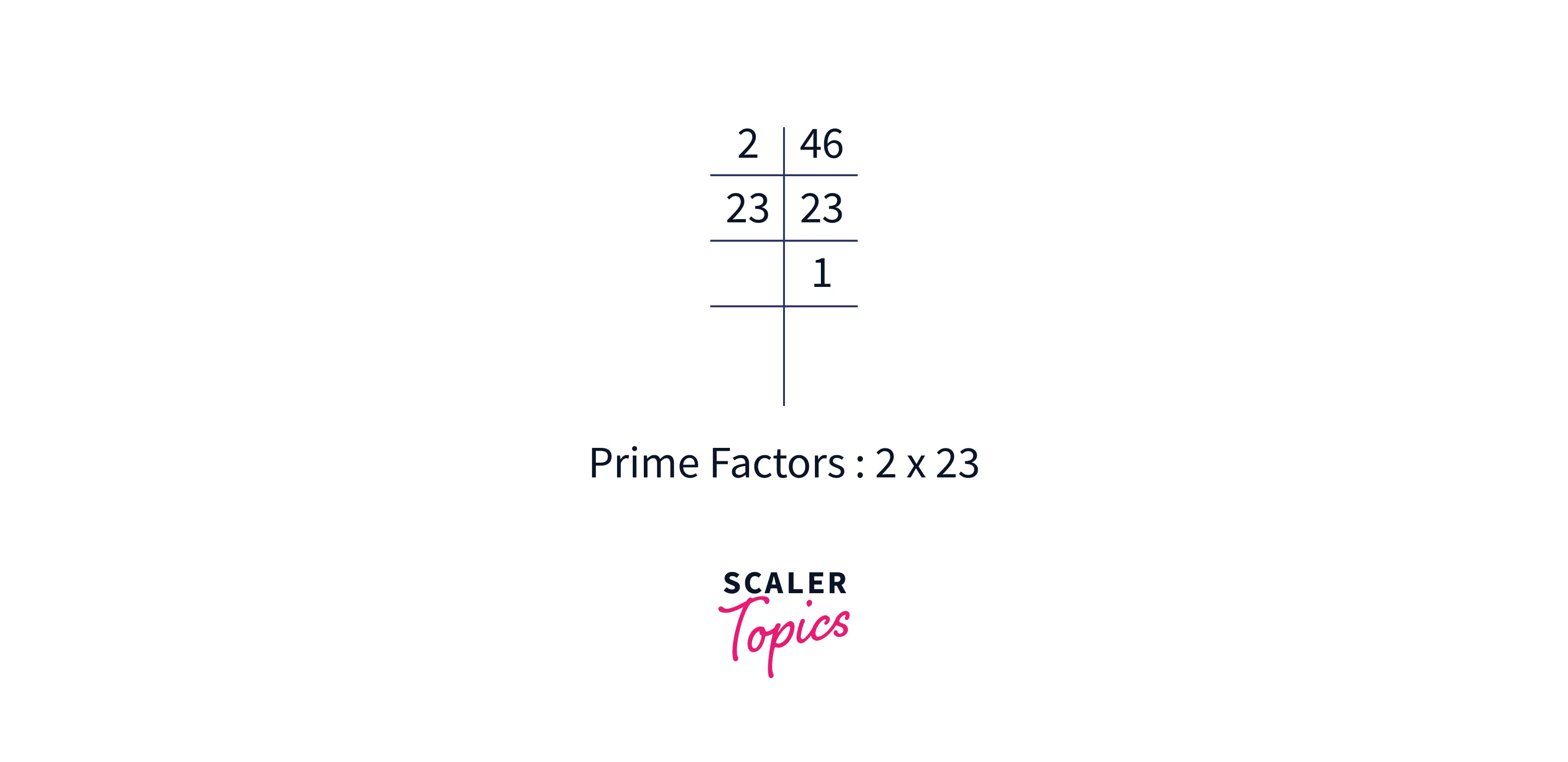
After dividing 46 with 2, there is no number till sqrt(46) that divides 46, therefore the loop will end but there is still a number that is a factor of 46, that is 23, therefore, the extra condition is applied to overcome this issue.