Fibonacci Series in JavaScript

A Fibonacci series is a mathematical numbers series that starts with fixed numbers 0 and 1. All the further next numbers can be generated using the sum of the last two numbers.
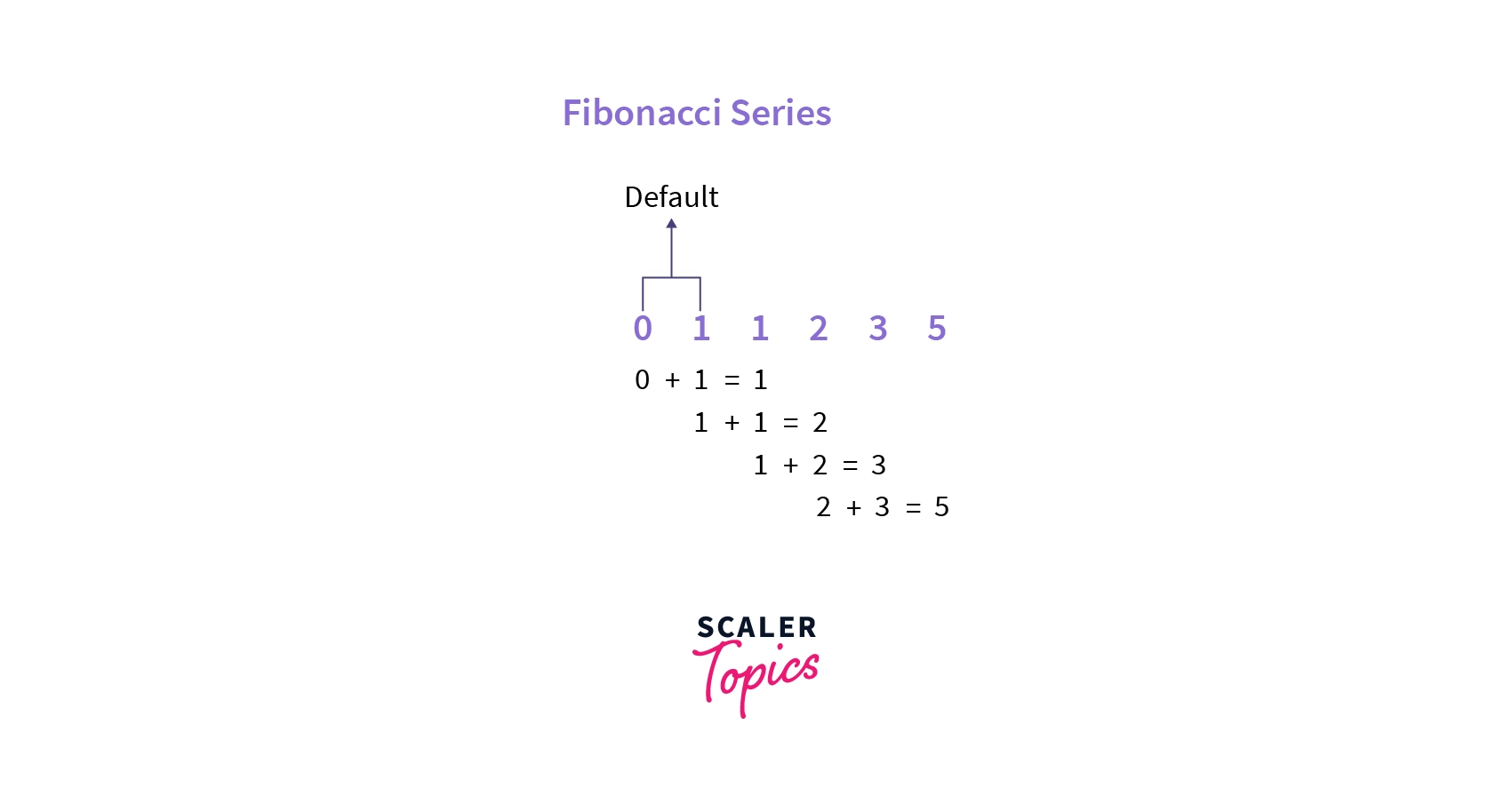
Representation of the Fibonacci series in JavaScript
As we have seen in the introduction section, the Fibonacci series in JavaScript is nothing but a mathematical sequence in which the current element is the sum of its previous two elements.
Note: The first two terms of the Fibonacci series in JavaScript are 0 and 1. The first two terms, i.e., 0 and 1, are always fixed.
So, we can generate the Fibonacci series using the sum concept. The order of the Fibonacci series is :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
As we can see that a term (say term) can be calculated using the last two terms. The term can be calculated using the last two terms i.e. and term.
We can formulate this sequence as:
where two numbers are fixed i.e. F(0) = 0 and F(1) = 1.
Refer to the picture shown below for better visualization.
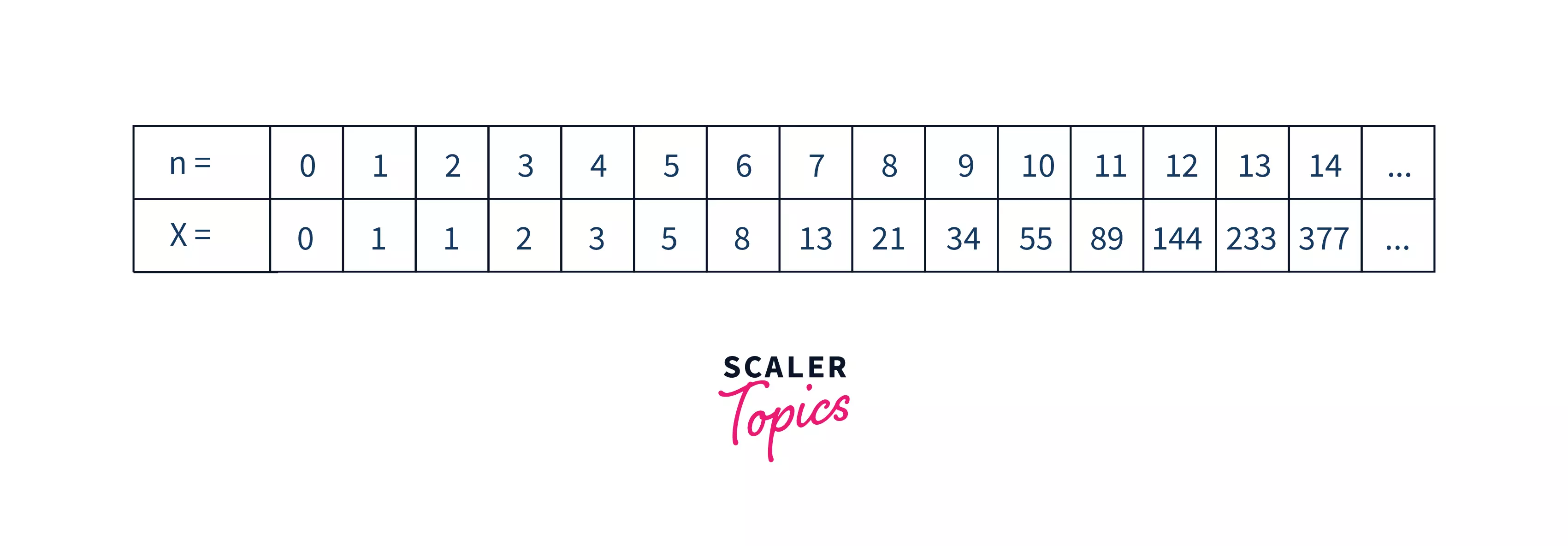
Here, the term is represented using X, and the number of the term is represented using N. So, here term 7 is called x7, which is equal to 13.
So, to generate the Fibonacci term, we can follow:
Steps to Find the Fibonacci Series of n Numbers
Now, that we have a good understanding of what is Fibonacci series in JavaScript, let us now learn about the steps to generate the Fibonacci series in JavaScript.
The flow chart of the Fibonacci Series can be represented as:
Step 1: Declare variables x, y, z, n, i. x, and y are storing the first two terms. n is the value of the term that needs to be calculated. z will store the sum of the previous two terms i.e. x and y. i is the number that will track the number of Fibonacci terms generated.
Step 2: Initialize variables as x = 1, y = 1, i = 2.
Step 3: Take the value of n from the user.
Step 4: Display the value of x and y.
Step 5: Repeat the process i.e., adding the previous two terms to generate the Fibonacci series until i > n. As:
- z = x+ y
- Print the value of the current term i.e. z.
- x = y, y = z
- i = i + 1
Step 6: Stop the process as i becomes equivalent to n. So, we have generated n terms of the Fibonacci series in JavaScript.
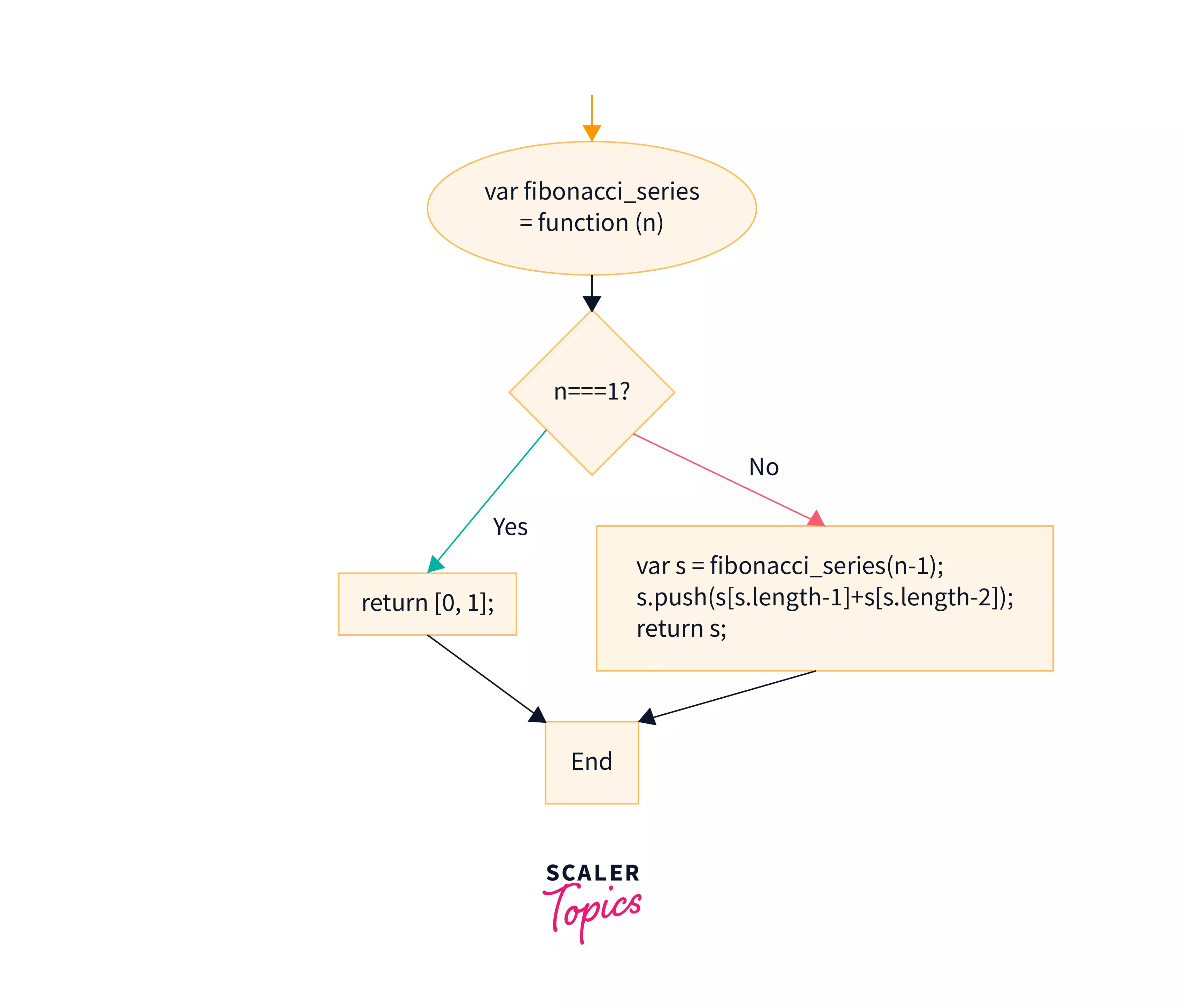
Note: A flowchart is a diagram that describes a process, system, or computer algorithm.
Examples of Fibonacci Series in JavaScript
As we now know the formula and steps to generate the Fibonacci series in javascript, let us now learn the different ways of generating the Fibonacci series in javascript by coding some examples.
Get the Fibonacci series up to n terms using for loop
A loop like for and while can be used to generate the Fibonacci series. We can run a loop from 2 to N, and in each iteration, the sum of the previous two elements is calculated and stored.
So, at the end of the nth iteration, we will have the nth Fibonacci term in front of us.
Let us code the above approach using for loop. Suppose we want to generate the term of the Fibonacci series in JavaScript.
Implementation:
Output:
Note: Since, we know the first two terms of the Fibonacci series in javascript, we ran our loop from the 2nd term to the nth term i.e. for(2 to N).
Time and Space Complexities
Since we are not storing the vales, the printing of the nth term is taking O(1) time on the other hand, the loop is running for (n-2) times which is equivalent to O(n). So, the overall time complexity of the above approach is O(n).
The space complexity is O(1) as as we are not taking any extra space(except some variables that takes O(1) space).
Get the Fibonacci series up to n terms using the while loop
Similar to the for loop approach shown above, we can generate the Fibonacci series in javascript using the while loop. Let us take an example to understand the code better.
Suppose we want to generate the term of the Fibonacci series in JavaScript.
Implementation:
Output:
Time and Space Complexities
Since we are not storing the vales, the printing of the nth term is taking O(1) time, on the other hand, the loop is running for (n-2) times which is equivalent to O(n). So, the overall time complexity of the above approach is O(n).
The space complexity is O(1) as we are not taking any extra space(except some variables that takes O(1) space).
Get the Fibonacci series of the first 8 terms
We can generate the entire Fibonacci series in javascript using the loop approach discussed above. We were only printing the nth term of the Fibonacci series in javascript. Let us store the elements in an array and then print the array to see the entire series up to N elements.
Implementation:
Output:
Get the Fibonacci series using the Recursion Function
Before getting into the example and code of the Fibonacci series using the Recursion Function, let us first get a brief understanding of recursion.
Recursion is a widely used technique in computer science used to solve complex problems by breaking the problem into simpler ones. Recursion is a process in which a function calls itself directly or indirectly. The corresponding function is called a recursive function.
We know that the first two terms of the Fibonacci series are fixed, i.e. 0 and 1. Suppose we want to generate the term of the Fibonacci series.
- The term can be calculated using the sum of the and terms. But both the and terms are currently unknown.
- Similarly, the term can be calculated using the sum of the and terms.
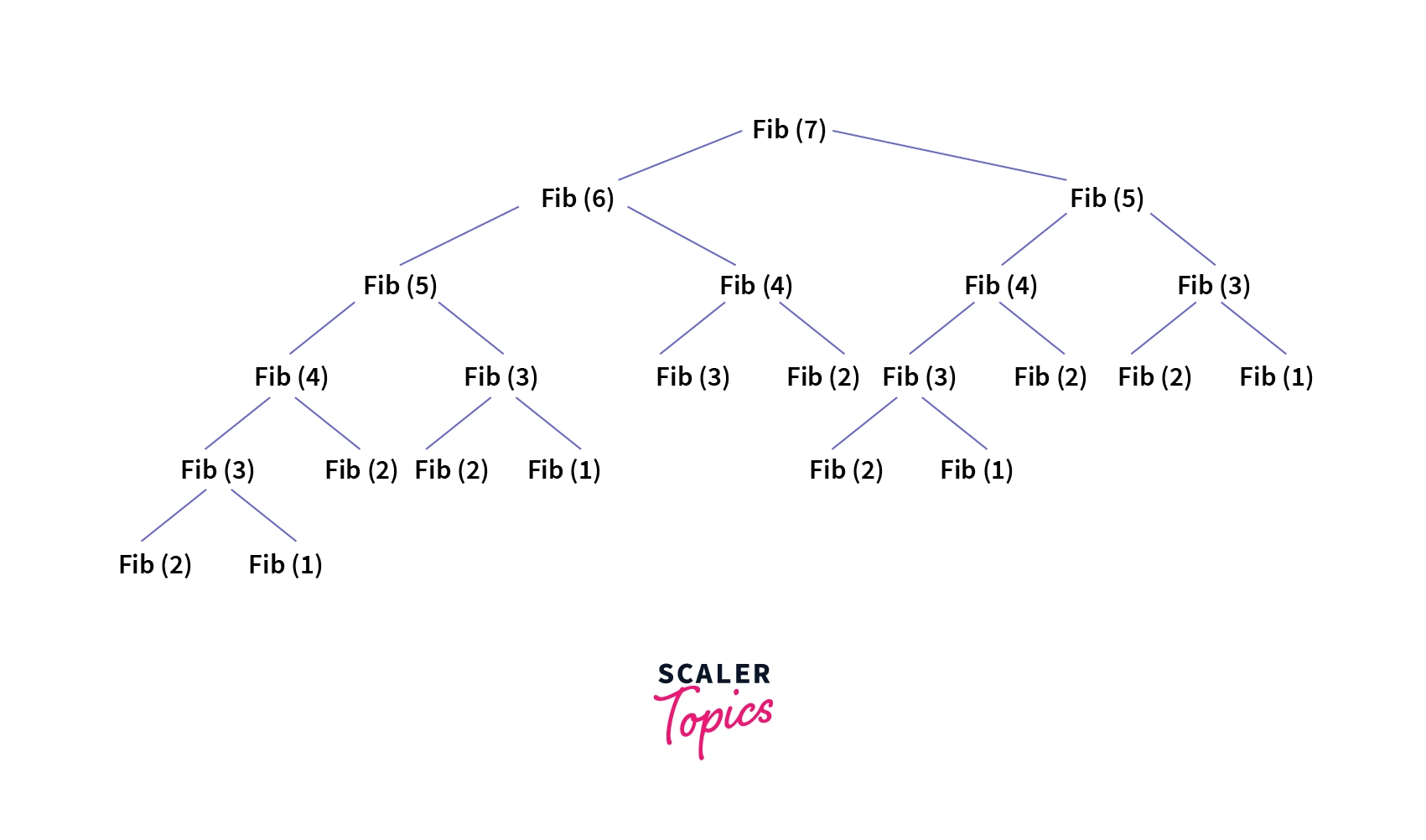
We can visualize these recursive calls as tree structures shown below.
Pseudocode for the recursive approach can be:
Suppose we want to generate the term of the Fibonacci series in JavaScript.
Implementation:
Output:
If we want to generate the entire series rather than the nth term, we can store each element or item inside an array as:
As we can see in the example diagram above, we have passed n = 7 to our function now we have to calculate for last two values that are which is but when we will calculate for , again will be calculated due to recursion. So, the Fibonacci series in JavaScript using recursion is not the best and most optimized implementation.
Time and Space Complexity
We can see that there is a lot of repetition of function in the case of the recursive approach. Time complexity is: O(2^n) Space complexity is: O(n), which comes out to be the maximum depth of the recursive tree.
Get the Fibonacci series in Reverse Order
We can also generate the reversed Fibonacci series in javascript using a loop or recursive approach. Let us take an example to visualize the code better.
Let us generate the Fibonacci series in javascript till term in reverse order.
Output:
Ready to conquer complex algorithms? Our Dynamic Programming Free Course is your ticket to success. Enroll today and elevate your coding proficiency!
Conclusion
- A Fibonacci series in JavaScript is a mathematical numbers series that starts with fixed numbers 0 and 1. All the further next numbers can be generated using the sum of the last two numbers.
- The term can be calculated using the last two terms i.e. and term.
- The Fibonacci series in JavaScript can be calculated in many ways, such as using Dynamic Programming, using loops, and using recursion.
- The Time Complexity of the recursive approach is , whereas the Space Complexity of the recursive approach is: .
- The Time Complexity of the loop approach is , whereas the Space Complexity of the loop approach is: .
- The Time Complexity of the reverse order is , whereas the Space Complexity of the reverse order is: .
