Fibonacci Series in Python using Recursion

Overview

A Fibonacci series is a mathematical numbers series that starts with fixed numbers 0 and 1. All the next numbers can be generated using the sum of the last two numbers. The $n th$ term can be calculated using the last two terms i.e. $(n - 1)th$ and $(n - 2)th$ term.

Fibonacci series in Python Using Recursion

Before learning how to generate the Fibonacci series in python using recursion, let us first briefly understand the Fibonacci series.

A Fibonacci series is a mathematical numbers series that starts with fixed numbers 0 and 1. All the following numbers can be generated using the sum of the last two numbers. Refer to the image below for a better understanding.

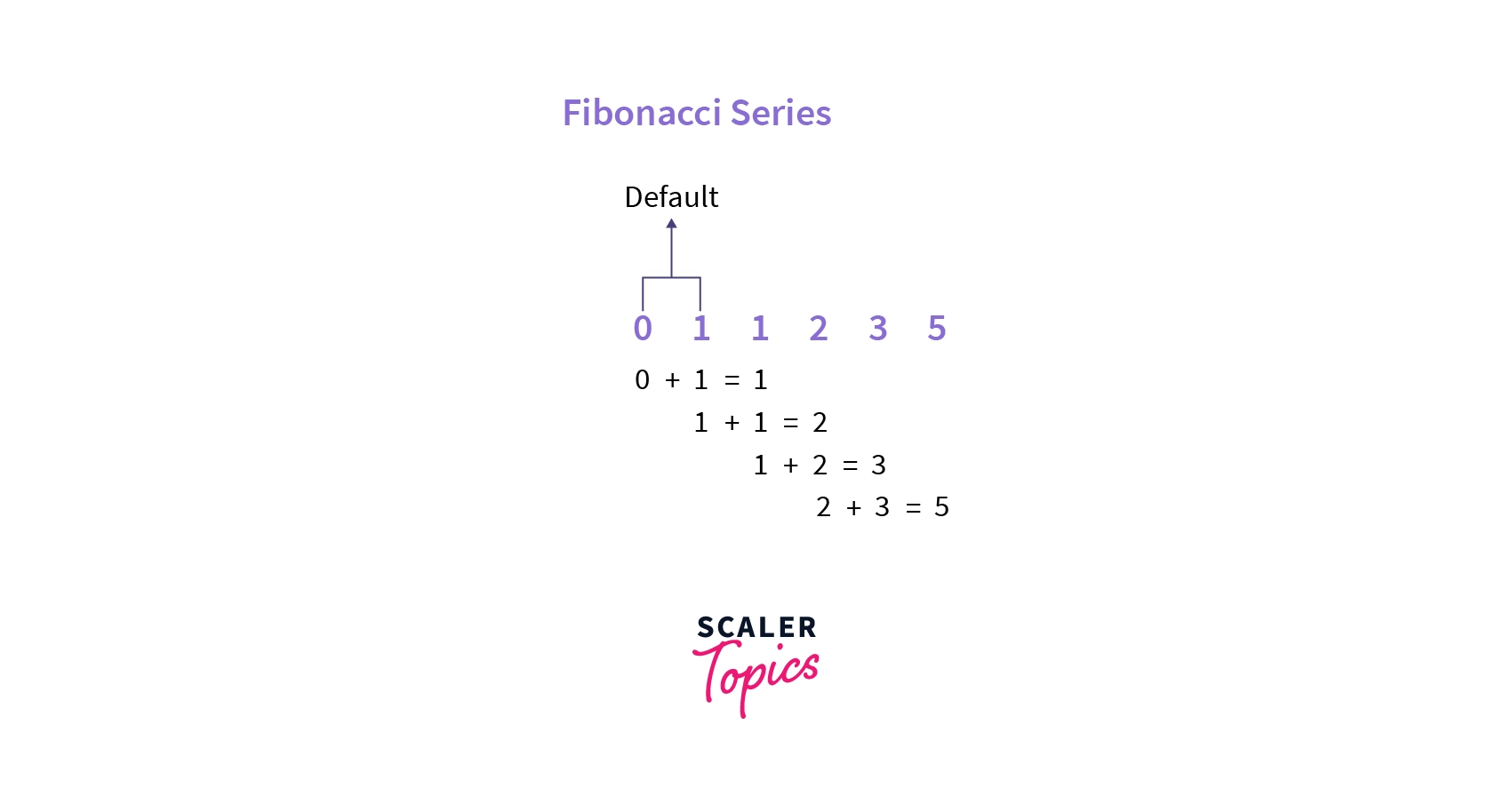
Fibonacci series

As shown in the diagram above, the first two digits are fixed, i.e.,0 and 1. The third term is calculated using the last two terms i.e $1 = (1 + 0)$ . Again, we calculated the fourth term by adding second and third terms, i.e., $2 = (1 + 1)$ .

Refer here to learn more about the Fibonacci series.

The Fibonacci series can be calculated in a lot of ways, such as:

Using Dynamic Programming
Using loops
Using recursion

Let us learn how to generate the Fibonacci series in python using recursion.

The order of the Fibonacci series is :
$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...$

We can see that a term (say $nth$ term) can be calculated using the last two terms. The $n$ th term can be calculated using the last two terms i.e. $(n - 1)th$ and $(n - 2)th$ term.

We can formulate this sequence as:

$F(n) = F(n - 1) + F(n - 2)$
where two numbers are fixed i.e. F(0) = 0 and F(1) = 1.

Function name: fibonacci(N)

Pseudocode for the recursive approach can be:

Refer to the example section below for code implementation.

Example

We know that the firth two terms of the Fibonacci series are fixed, i.e., 0 and 1. Suppose we want to generate the 7th term of the Fibonacci series.

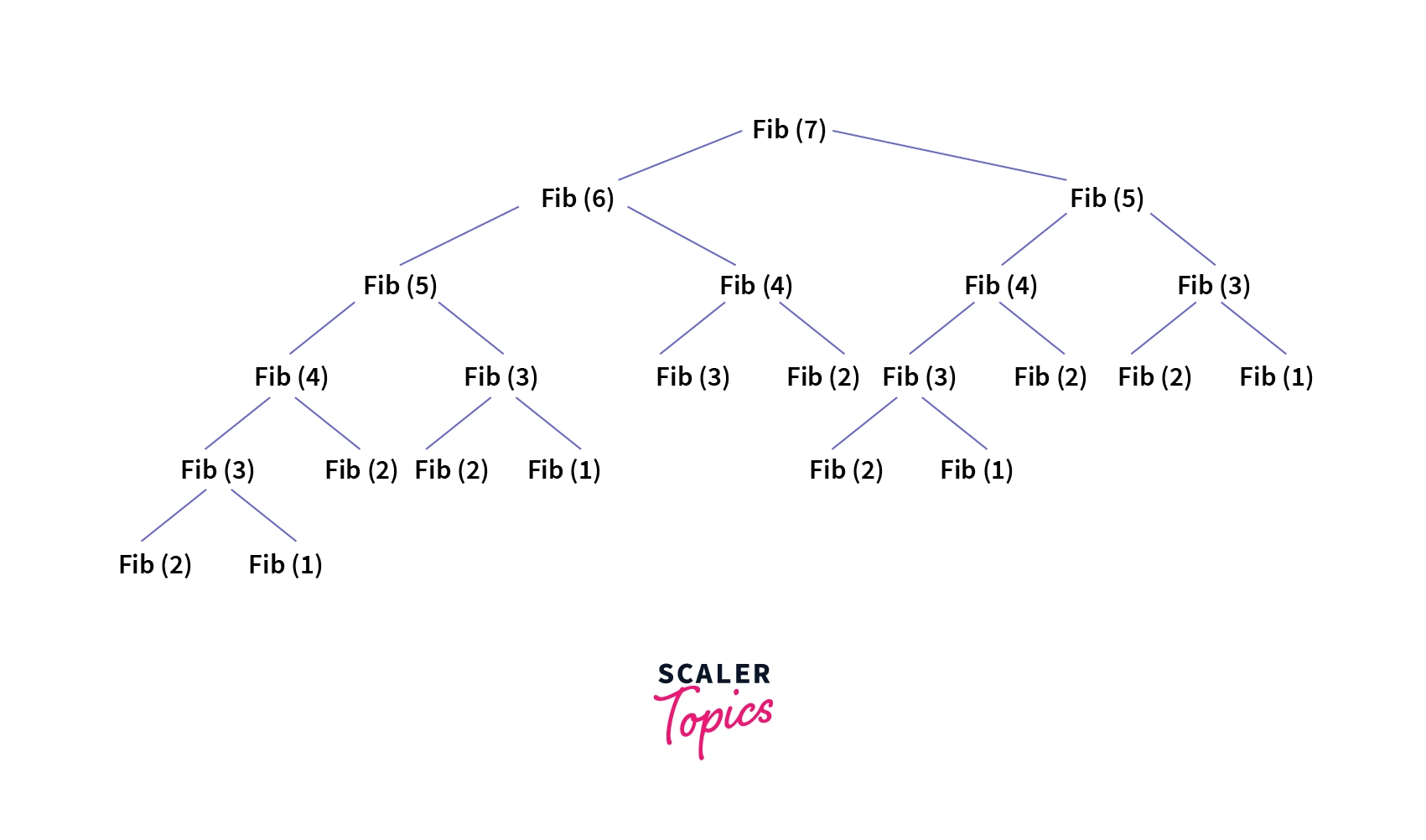
The 7th term can be calculated using the sum of the 5th and 6th terms. But both the 5th and 6th terms are currently unknown.
Similarly, we can calculate the 5th term by adding the 4th and 3rd terms. We can visualize these recursive calls as tree structures shown below.

[IMAGE_2 Use the same image] recursive calls as tree structures

The code implementation of the same:

Output:

We can also generate the series if we invoke the Fibonacci function in a loop. Let us see the implementation.

Output:

As we can see in the example diagram above, we have passed n = 7 to our function $fibonacci(7)$ now we have to calculate for last two values that are $fibonacci(7-1) + fibonacci(7-2)$ which is $fibonacci(6) + fibonacci(5)$ but when we will calculate for $fibonacci(6)$ , again $fibonacci(5)$ will be calculated due to recursion. So, the Fibonacci series in python using recursion is not the best and most optimized implementation.

Time and Space Complexities
Time complexity is: $O(n)$ Space complexity is $O(n)$ , which is the maximum depth of the recursive tree.

Ready to conquer complex algorithms? Dynamic Programming Course by Scaler Topics is your ticket to success. Enroll today and elevate your coding proficiency!

Conclusion

A Fibonacci series is a mathematical numbers series that starts with fixed numbers 0 and 1. All the following numbers can be generated using the sum of the last two numbers.
The $n$ th term can be calculated using the last two terms i.e. $(n - 1)th$ and $(n - 2)th$ term.
The Fibonacci series can be calculated in many ways, such as using Dynamic Programming, loops, and recursion.
The time complexity of the recursive approach is $O(n)$ , whereas the space complexity of the recursive approach is: $O(n)$

Fibonacci Series in Python Using Recursion

Overview

Fibonacci series in Python Using Recursion

Example

Conclusion

Read More: