Filtering in Image Processing
Overview
Filtering in image processing is a fundamental technique used to enhance the quality of images. It involves the application of mathematical operations to an image to extract important features, remove noise, or blur images. Image filtering is an essential step in various image processing applications such as computer vision, medical imaging, and satellite imagery.
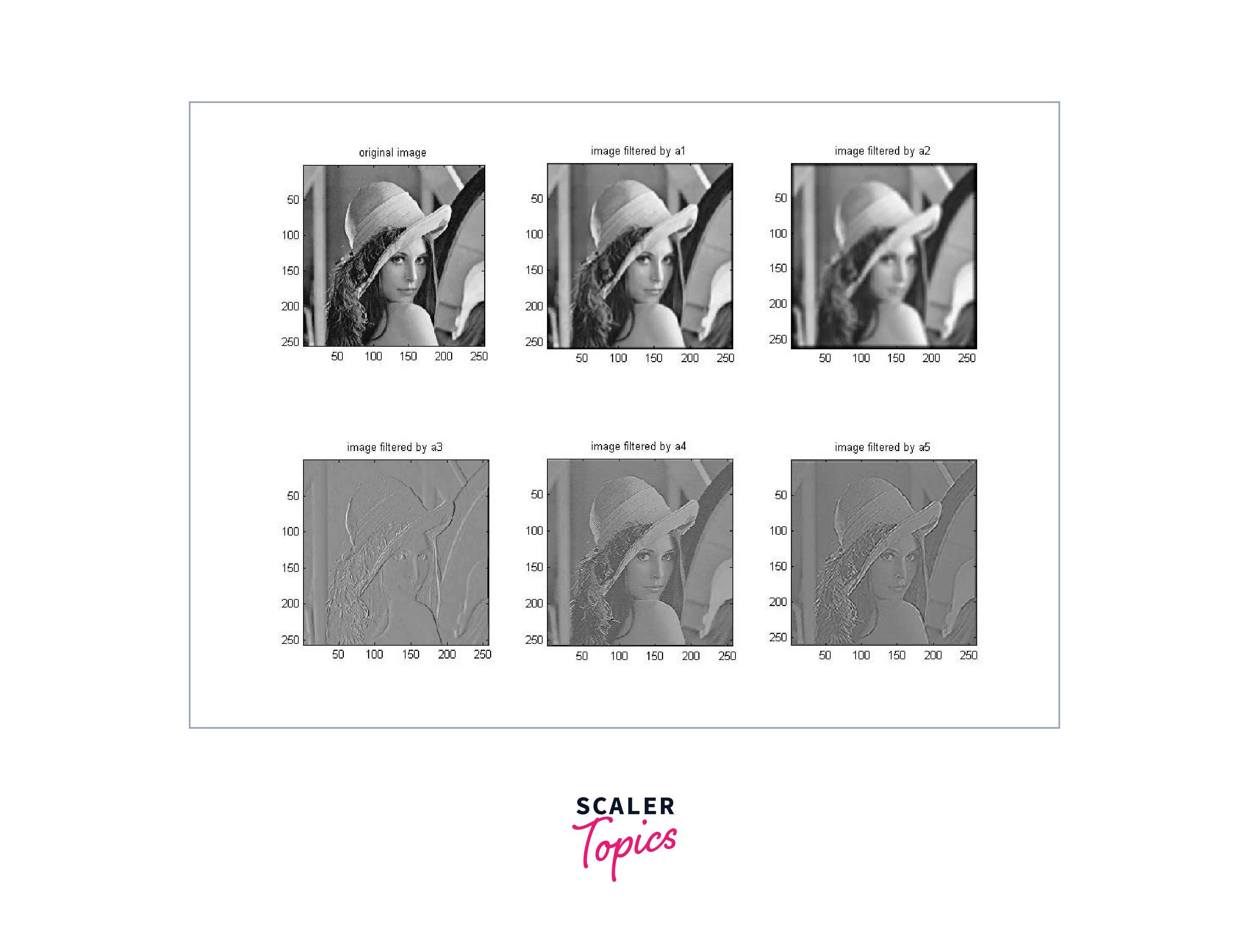
Image Filtering
Images as Functions
In image processing, an image is treated as a function f(x,y), where x and y are the spatial coordinates of the image. Each pixel in the image represents a value of this function at a specific location. The values of this function can be manipulated using various image-processing techniques, including filtering.
Mathematically, an image function can be defined as:
where (x, y) are the spatial coordinates of a pixel in the image, I is the intensity value at that pixel location, and f(x,y) is the image function. For grayscale images, the intensity value I is usually a single value representing the brightness of the pixel. For color images, the intensity values represent the intensities of the red, green, and blue (RGB) color channels.
The image function can be discretized and represented as a matrix or an array of values. The size of the matrix corresponds to the dimensions of the image, and each element of the matrix represents the intensity value of a pixel in the corresponding location.
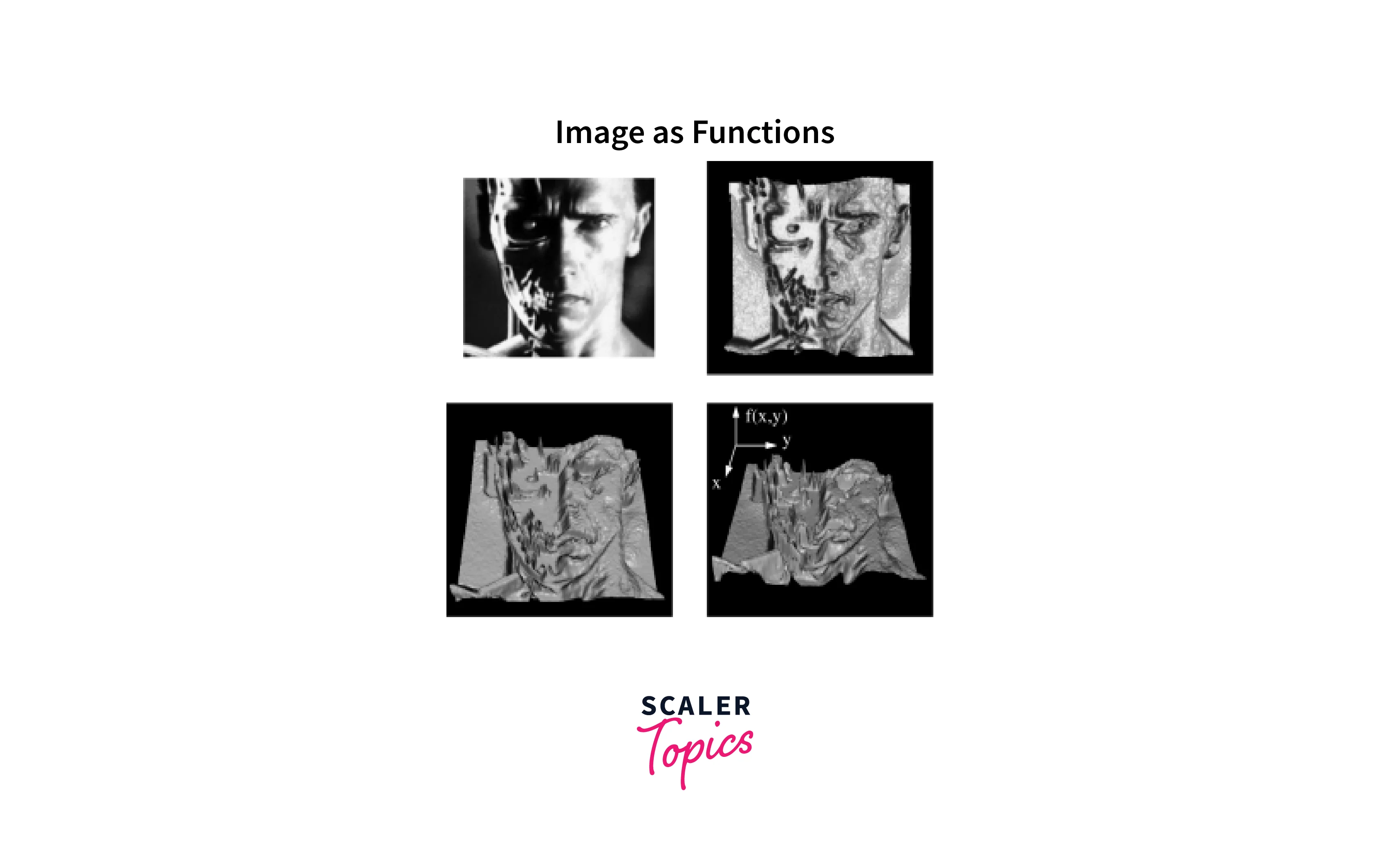
Image Processing
Image processing is the use of mathematical and computational algorithms to transform or analyze digital images. To do this, it uses image processing filters. It includes tasks such as image enhancement, restoration, segmentation, and recognition.
There are two main categories of image processing: analog and digital. Analog image processing involves using optical techniques and analog devices to manipulate and analyze images. Digital image processing, on the other hand, involves using digital algorithms and computers to process images.
It involves several steps, including image acquisition, preprocessing, segmentation, feature extraction, object recognition, and postprocessing. Image processing techniques are used in various applications, including medical imaging, remote sensing, and computer vision.
2D Convolution
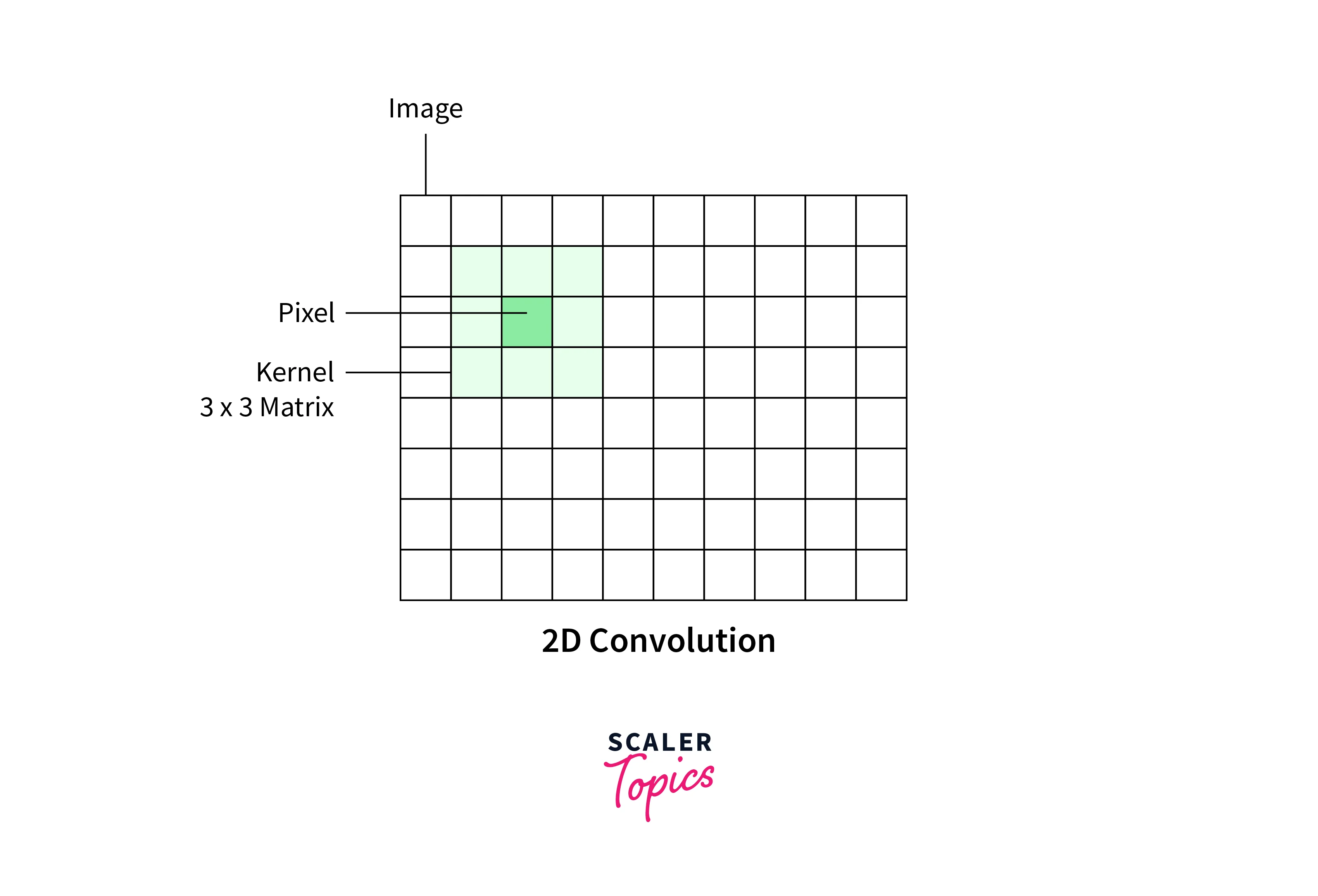
2D convolution is a mathematical operation used for filtering in image processing to apply a filter to an image. It involves sliding a kernel over the image and computing the dot product between the kernel and the corresponding pixel values.
2D convolution is an operation used for filtering in image processing to modify an image by applying a filter or kernel to it. The filter is a matrix of numbers that is "slid" over the image, and the result of the convolution operation is a modified image where each pixel is a weighted sum of its neighboring pixels.
Mathematically, the 2D convolution operation is defined as:
to to
where,
| Term | Meaning |
|---|---|
| g(x,y) | The modified image |
| f(x,y) | The original image |
| h(i,j) | The filter or kernel |
| k | The half-size of the filter (the filter size is 2k+1 by 2k+1) |
The convolution operation is performed for each pixel in the image, and the resulting modified image is obtained by plotting the values of g(x,y) at each pixel location.
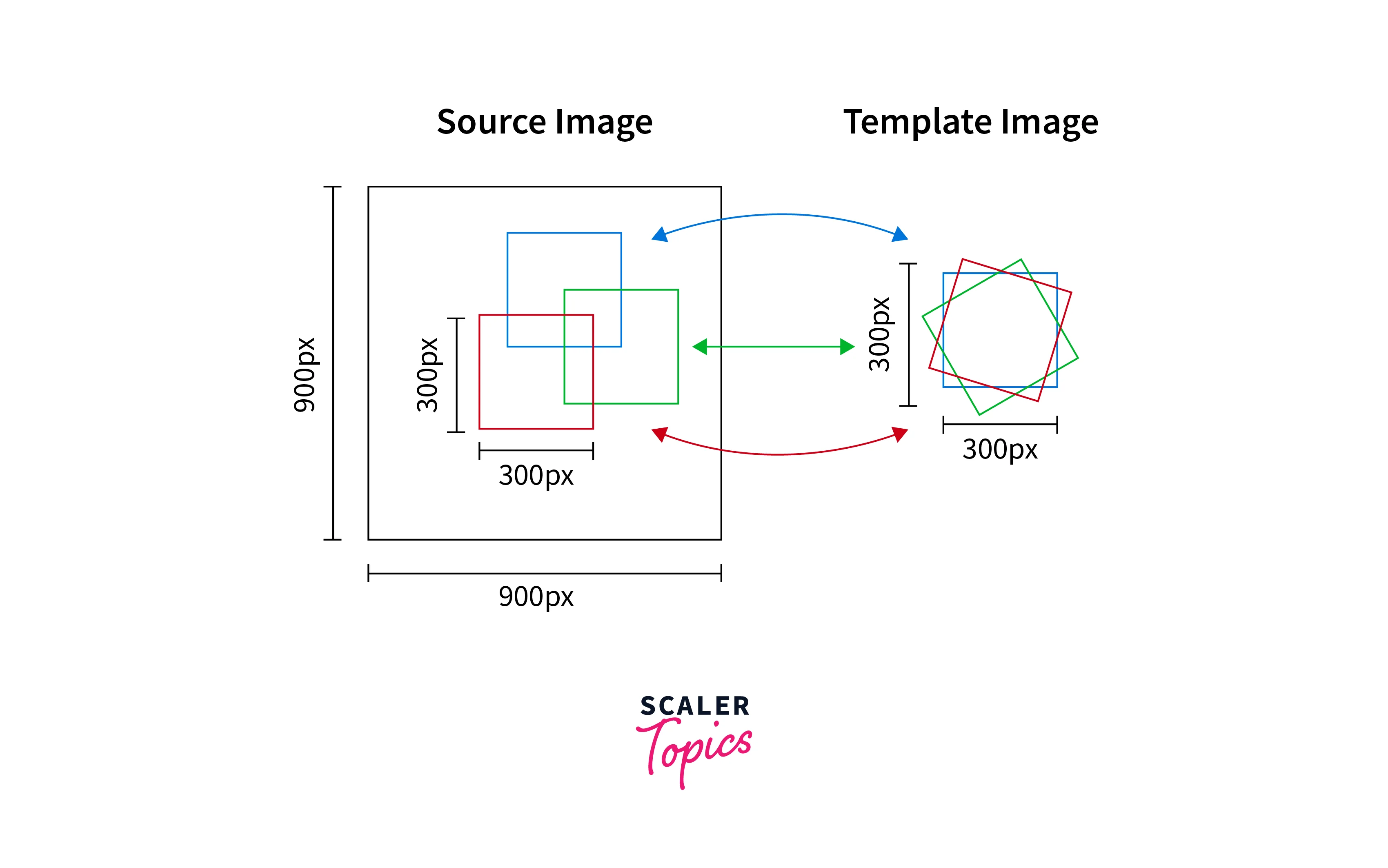
Correlation
Correlation is a mathematical operation used in the domain of filtering in image processing to measure the similarity between two images or between a filter and an image. It involves sliding a kernel over an image and computing the dot product between the kernel and the corresponding pixel values.
The correlation operation can be performed using Fourier transforms, similar to convolution. This involves transforming the input image and the template into the frequency domain using the Fourier transform, multiplying them together, and then transforming the result back to the spatial domain using the inverse Fourier transform.
The correlation operation can be used for various filtering in image processing tasks, such as template matching, object recognition, and motion tracking. For example, in template matching, a small template image is compared to different locations in a larger input image to find the best match.
There are two types of correlation: normalized cross-correlation and phase correlation. Normalized cross-correlation scales the correlation map to have values between -1 and 1, where 1 indicates a perfect match between the template and the input image. Phase correlation is a variation of correlation that works in the frequency domain and is more robust to image noise and illumination changes.
Mathematically, the correlation operation between two images, f, and g, is defined as:
to to
where,
| Term | Meaning |
|---|---|
| r(x,y) | The correlation map, which measures the similarity between f and g |
| f(x,y) | The input image |
| g(i,j) | The template or reference image |
| k | The half-size of the template |
Edge Detection
Edge detection is a technique used in the field of filtering in image processing to identify the boundaries between objects in an image. It involves applying filters that highlight changes in pixel values, such as the Sobel or Canny filter.
Edge detection is an important operation in image processing that is used to identify boundaries between different regions in an image. It is typically performed using filters or operators that highlight regions with high gradients or rapid changes in intensity. The gradient magnitude and direction can be computed using partial derivatives, and the filtered image is thresholded to produce a binary image of edges.
Here is the table summarizing the equations for computing the gradient magnitude and direction in Edge detection:
| Term | Equation |
|---|---|
| Gradient of f with respect to x | |
| Gradient of f with respect to y | |
| Gradient magnitude (G) | |
| Gradient direction (θ) |
What are Filters?
Image processing filters are used to enhance or modify an image by altering the values of its pixels. Filters are mathematical operations that can be applied to an image using convolution or correlation. They can be used to smooth an image, remove noise, sharpen edges, or extract specific features.

Common types of image processing filters used in image processing include Gaussian filters, which blur an image to reduce noise, and Sobel filters, which highlight edges in an image. Other filters include median filters, which remove salt and pepper noise, and Laplacian filters, which enhance the contrast of an image.
Filtering in image processing can be designed to be adaptive, meaning they change their behavior based on the content of the image. Adaptive filters are useful in situations where the properties of an image vary across different regions. Overall, filters are an important tool in image processing, allowing for the enhancement and modification of digital images.

Techniques in Image Filtering
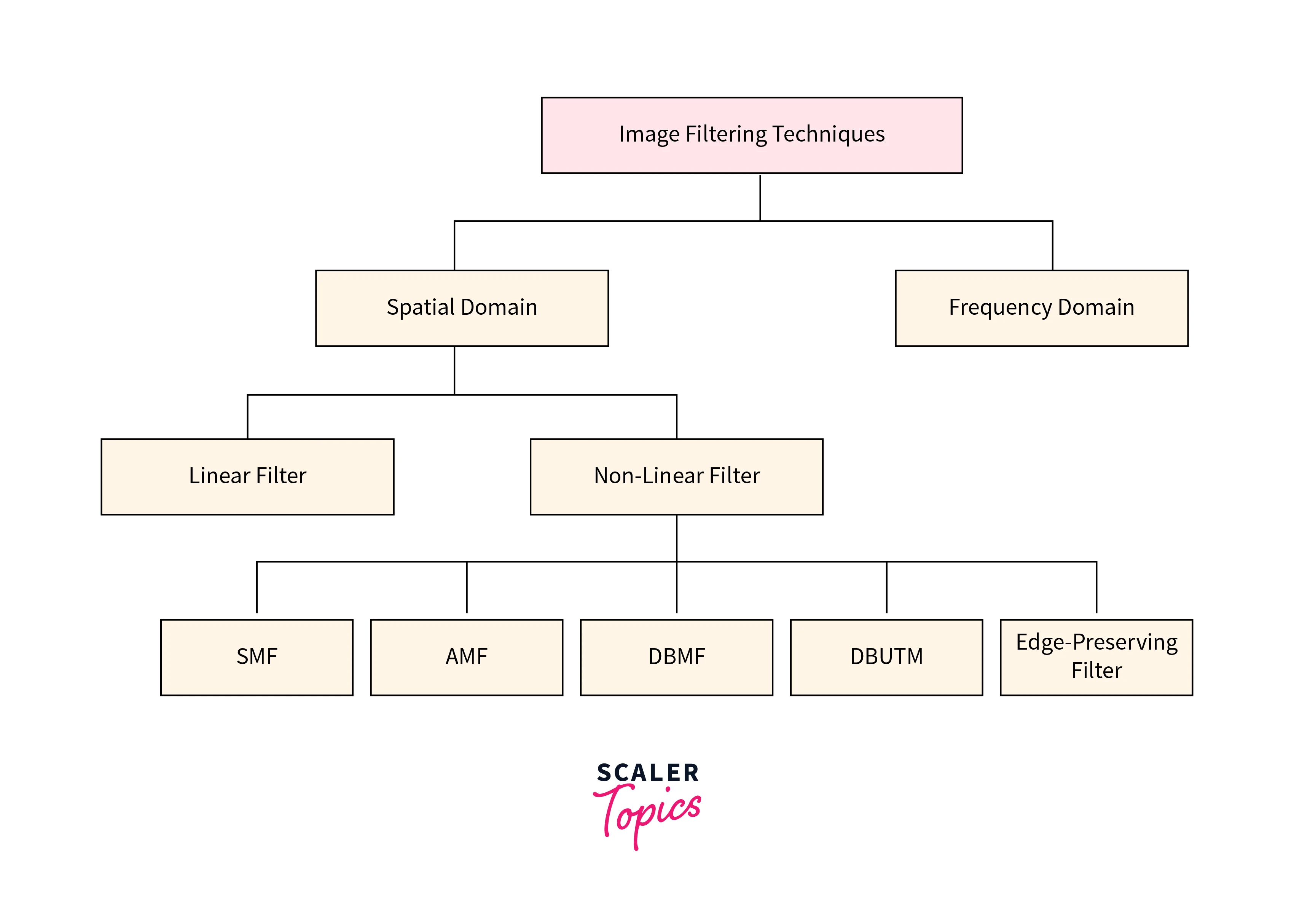
Filtering in image processing contains two major techniques. Image processing filters and their techniques are categorized based on spatial and frequency domains.
Spatial Domain
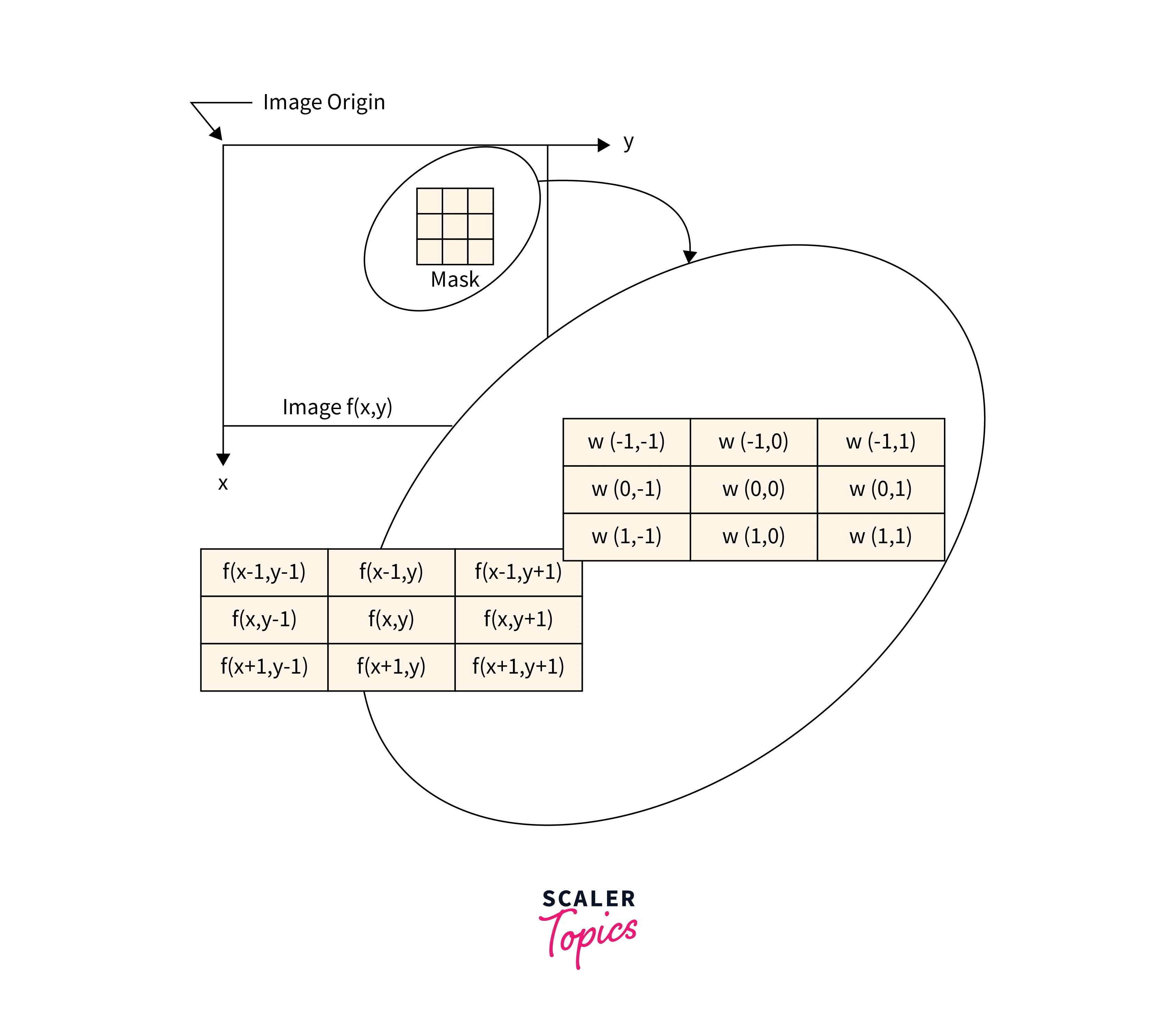
Spatial domain filtering in image processing techniques operates directly on the pixel values of an image in its spatial domain. This includes linear and non-linear spatial filters. These filters can be applied to an image to achieve various effects, such as smoothing, sharpening, or edge detection.

Linear Spatial Filter
A linear spatial filter operates on an image by applying a weighted sum of neighboring pixel values to each pixel. Common linear filters include Gaussian and Sobel filters, which can be used for smoothing and edge detection, respectively.
Non-linear Spatial Filter
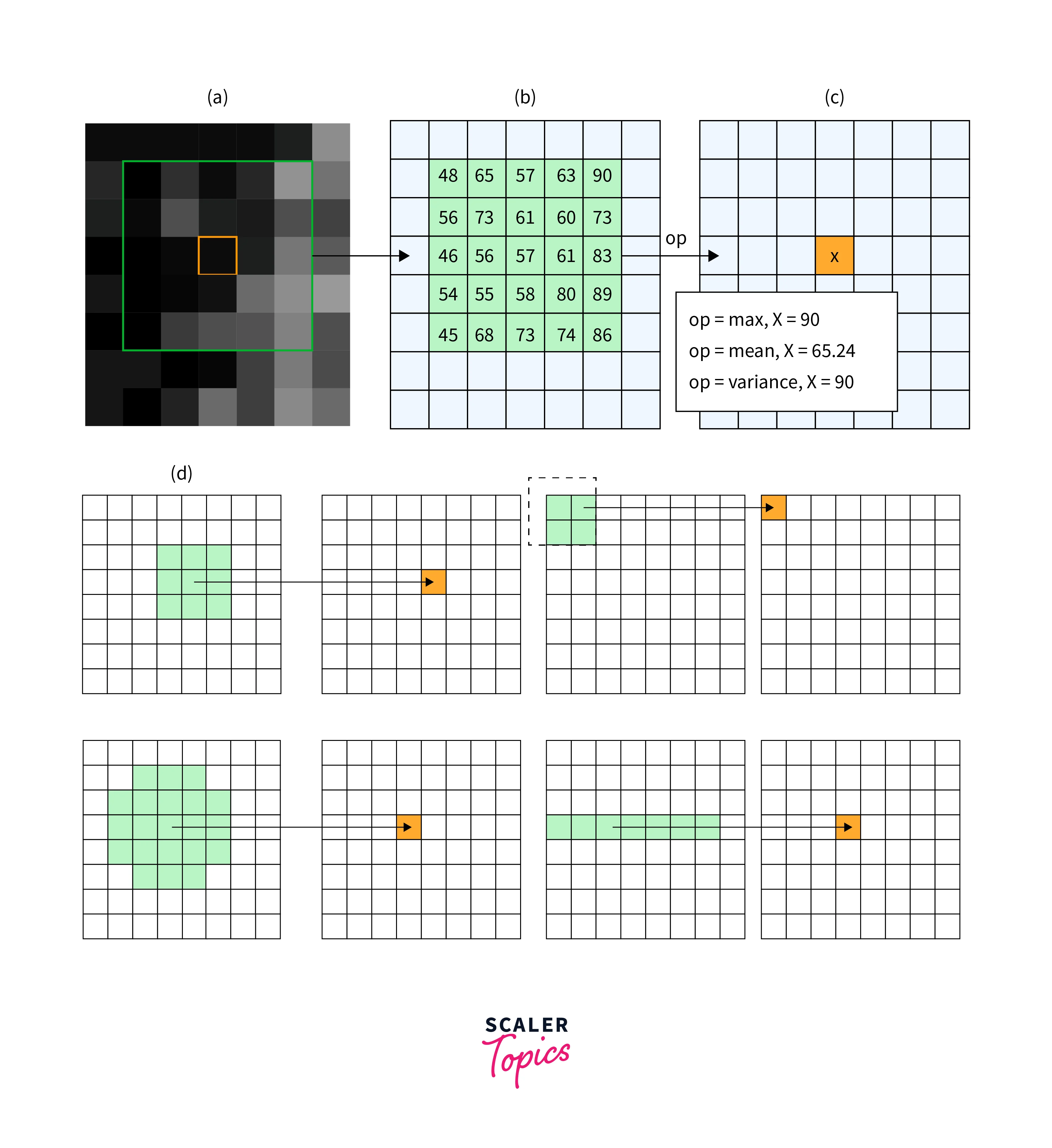
Unlike linear filters, non-linear spatial filtering in image processing operate on an image by applying a non-linear operation to the pixel values. This includes median and max filters, which are used for removing noise and enhancing contrast.
Implementation of Spatial Filter in OpenCV
Here is a sample Python code that uses OpenCV library to implement spatial filtering in image processing:
In this code, we first load the input image using the cv2.imread() function**. We then define the kernel size and type. In this example, we have defined three kernel types: identity, edge detection, and box blur. We then create the kernel based on the kernel type.
After creating the kernel, we apply it to the input image using the cv2.filter2D() function. Finally, we display the original and filtered images using the cv2.imshow() function and wait for the user to press any key to close the windows using the cv2.waitKey() and cv2.destroyAllWindows() functions.
Output
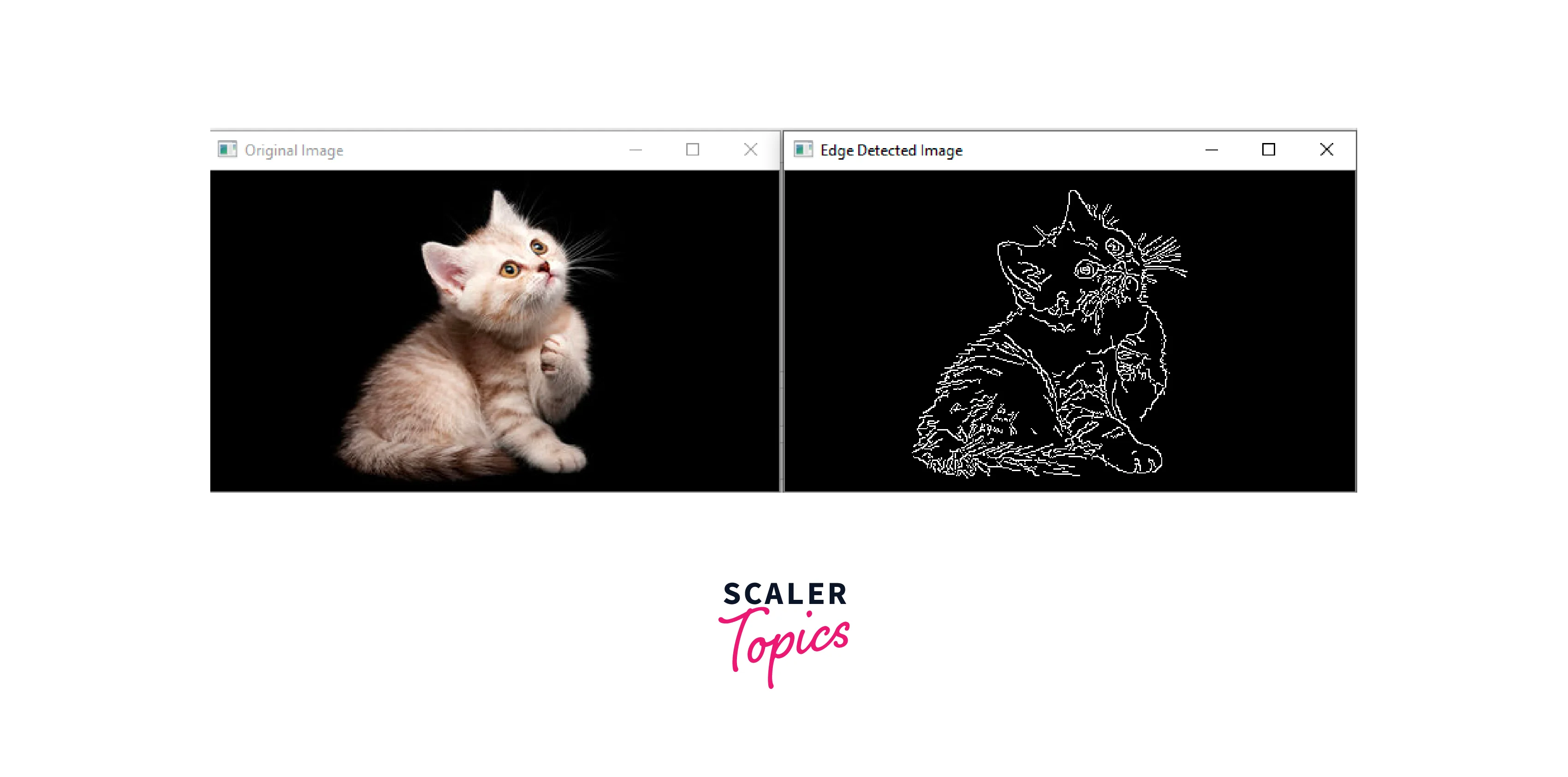
The output of the code will depend on the input image and the type of kernel used for filtering. Assuming that the input image is named "input_image.jpg" and is located in the same directory as the Python code, the code will read the image, apply the specified kernel to the image, and display the original and filtered images in separate windows.
For example, if the input image is a grayscale image of a cat, and the kernel type is "edge_detection" with a kernel size of 3x3, the output of the code could look like this:

Frequency Domain
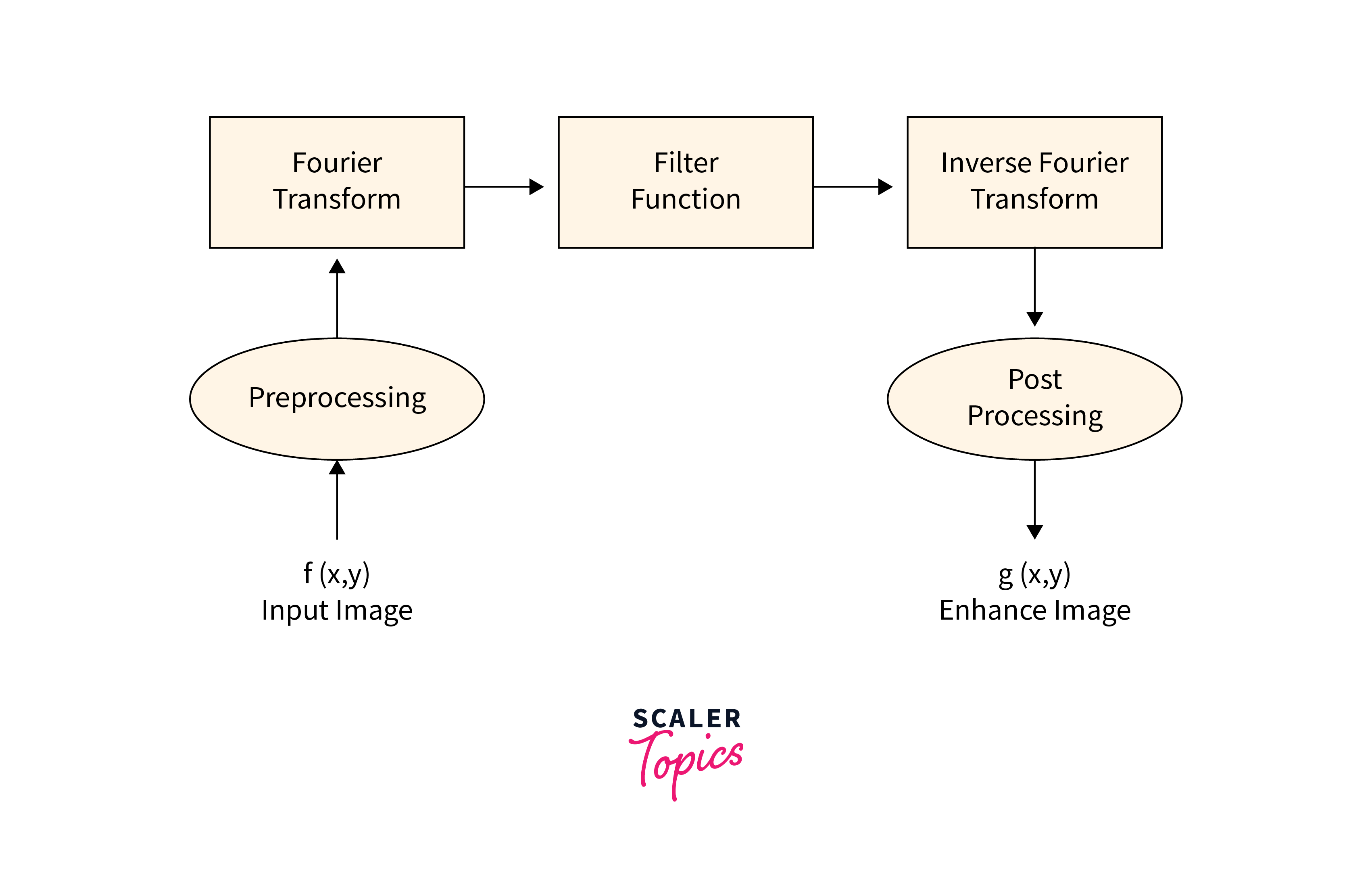
Frequency domain filtering in image processing techniques operate on the frequency components of an image. This includes Fourier transforms, which decompose an image into its frequency components and filters that can be applied in the frequency domain to achieve various effects, such as sharpening or blurring an image.
Histogram Modification
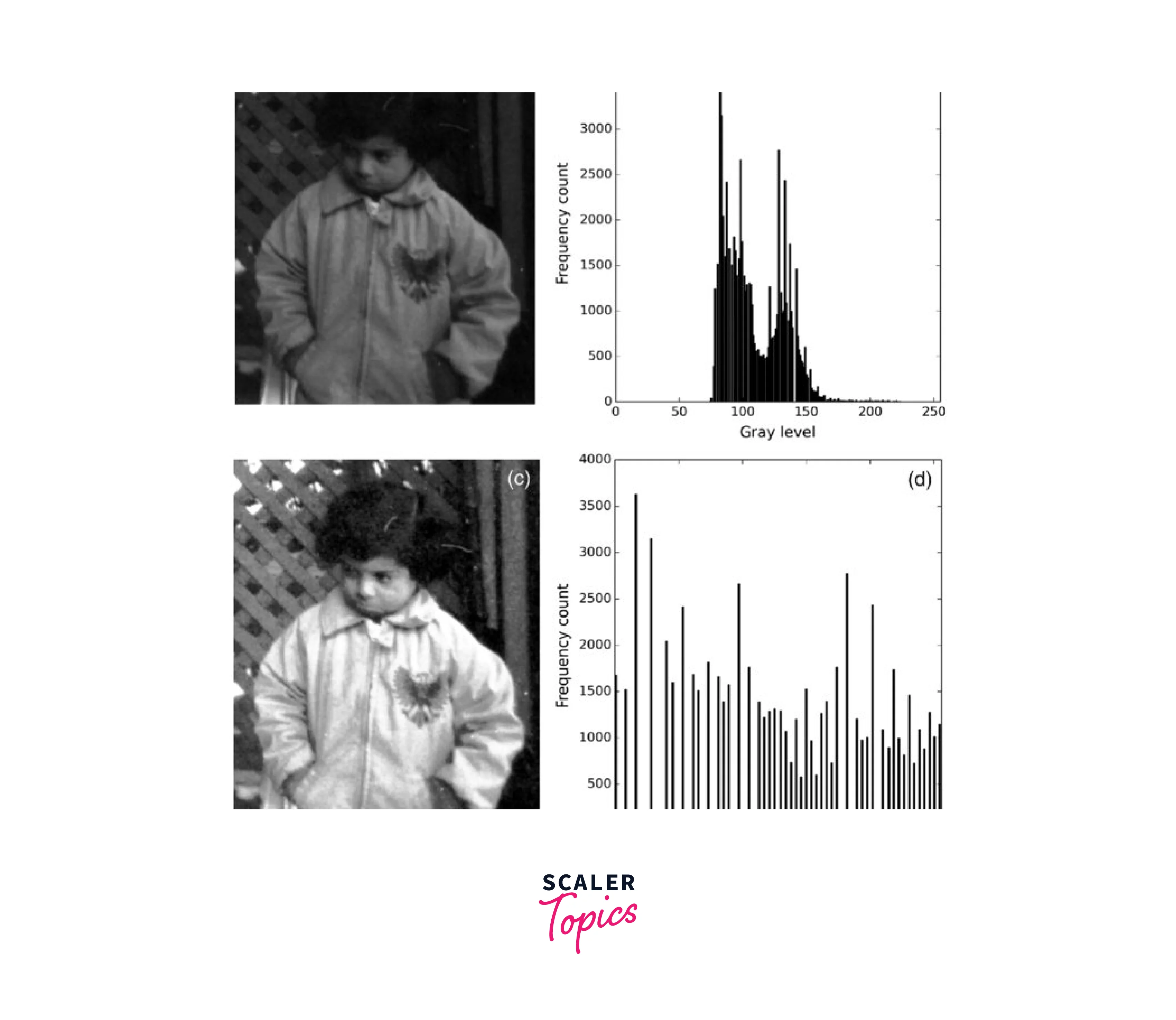
Histogram modification for filtering in image processing is a technique used to adjust the contrast and brightness of an image. It involves changing the distribution of pixel values in an image to enhance certain features or remove unwanted ones. Histogram modification is widely used in image processing, computer vision, and machine learning applications.
The most common types of histogram modification techniques are histogram equalization and histogram stretching. Histogram equalization is a technique that aims to spread out the histogram of an image, making it more uniform. This technique is particularly useful for enhancing the contrast of images that have low contrast.
Linear Systems
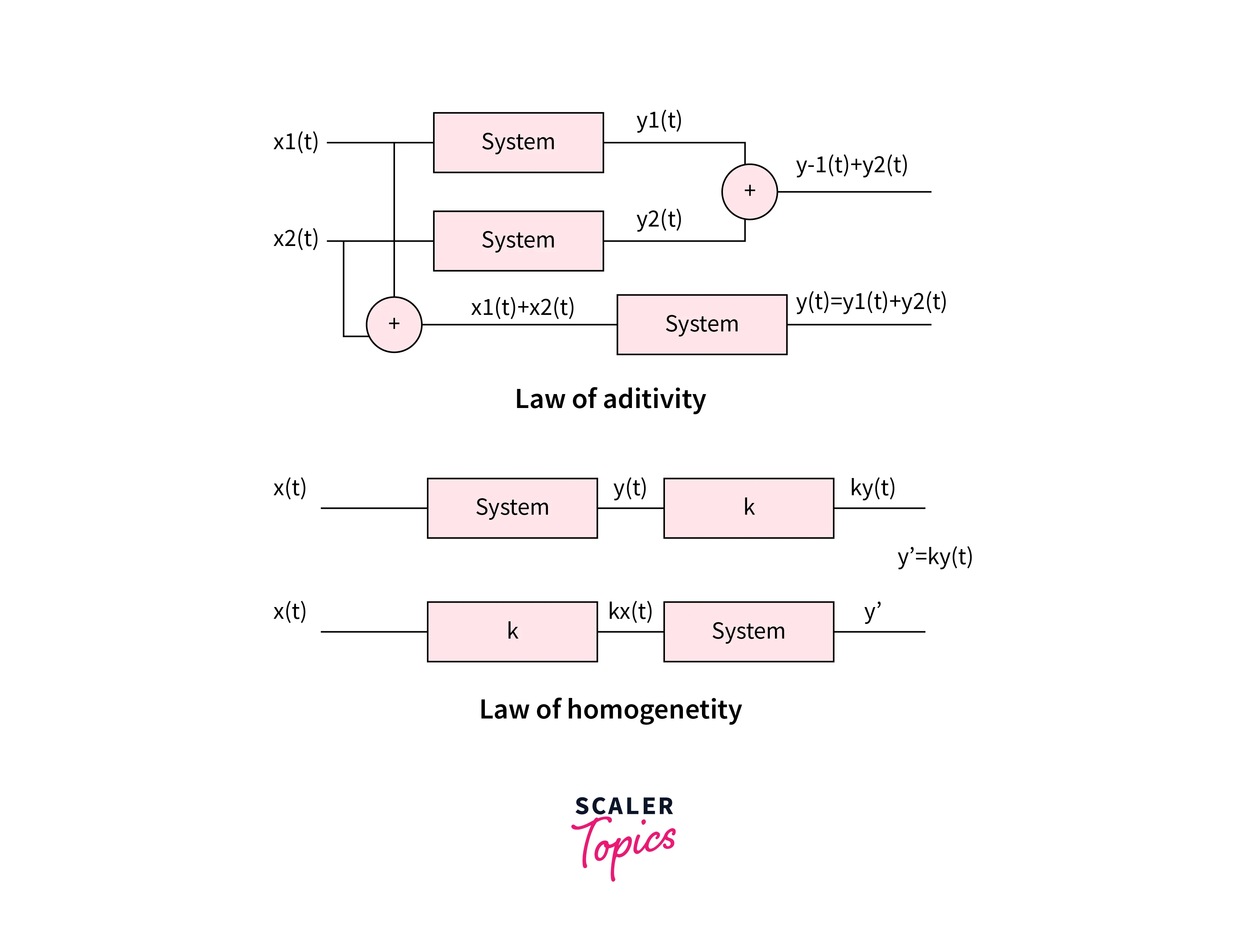
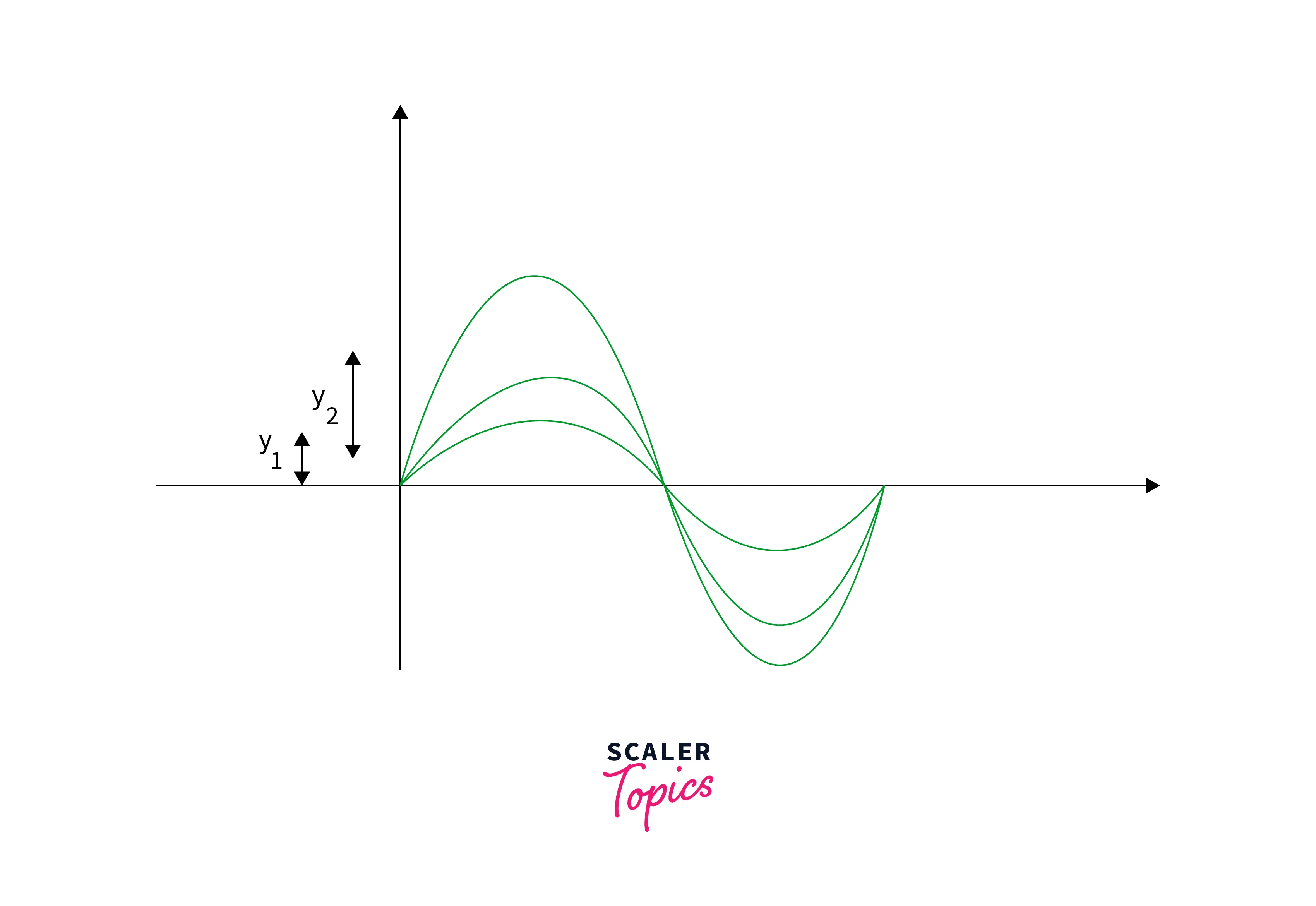
Linear systems are a fundamental concept in mathematics, physics, and engineering. A linear system is a system that satisfies two important properties: linearity and homogeneity. Linearity means that the system's output is proportional to its input, and homogeneity means that the system's response to a scaled input is also scaled by the same factor.
The filtering in image processing can be analyzed using mathematical tools such as Fourier transforms, Laplace transforms, and state-space analysis. These tools allow engineers to predict the behavior of linear systems under different conditions and design systems that meet specific performance requirements.
Mathematically, a linear system can be described using a linear operator, which is a function that maps one function to another. In the context of image processing, the input image is the function that is being mapped, and the output image is the function that is produced by the linear operator. The linear operator is usually defined by a matrix or a convolution kernel.
One important property of linear systems is that they satisfy the principle of superposition, which means that the output of a linear system to the sum of two inputs is equal to the sum of the outputs of the linear system to each input. This property allows for the efficient computation of complex image processing operations by breaking them down into simpler operations that can be performed separately and then combined.
Different Types of Filters
Linear Filters
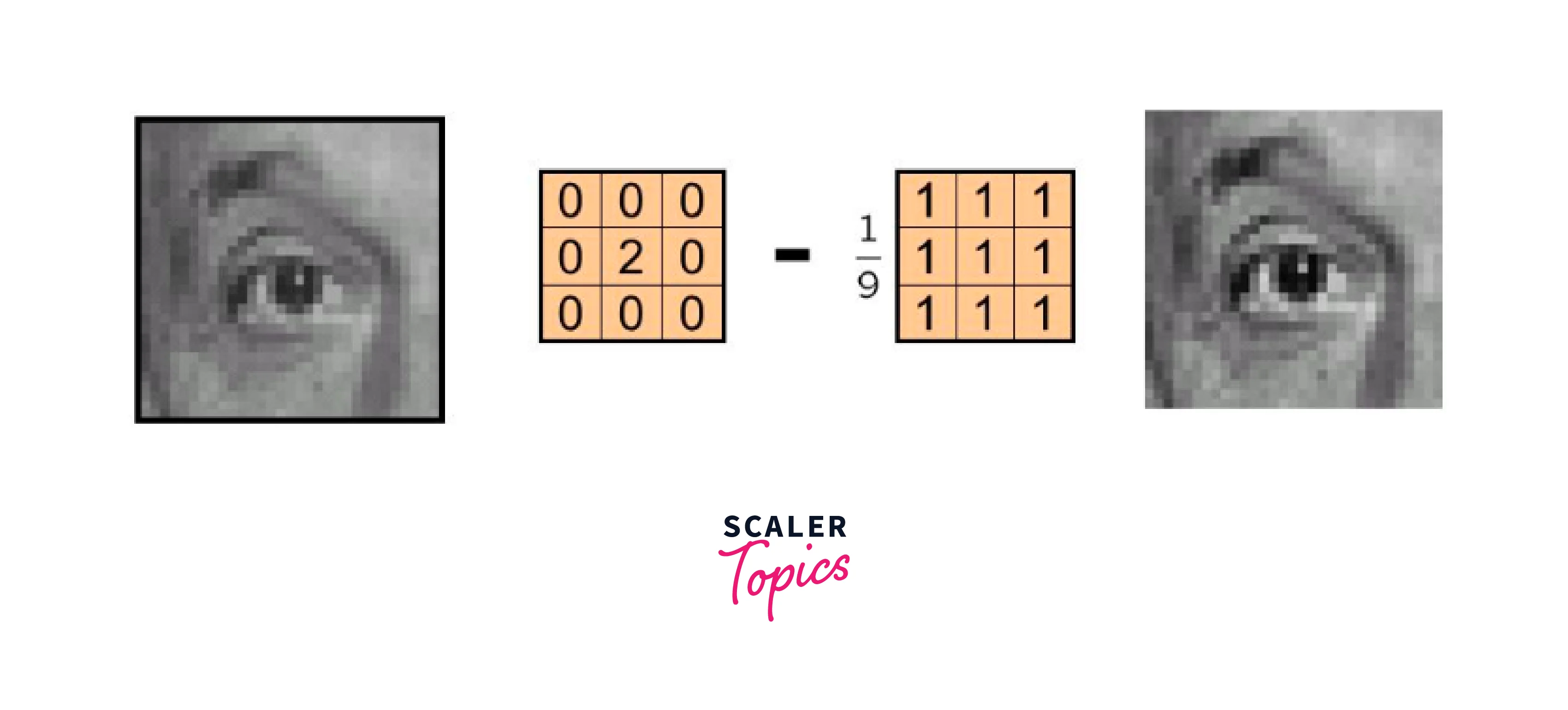
Linear filtering in image processing techniques involve convolving an image with a kernel or filter matrix to obtain a desired output. Examples include mean and box filters, which blur an image to remove noise, and Laplacian filters, which enhance edges and edges.
Non-linear Filters
Non-linear filters, on the other hand, are filtering in image processing techniques that modify pixels based on their local neighborhood, rather than simply convolving them with a fixed kernel. Examples of image processing filters include the median filter, which replaces each pixel with the median value of its local neighborhood, and the neighborhood average filter, which replaces each pixel with the average value of its neighboring pixels.
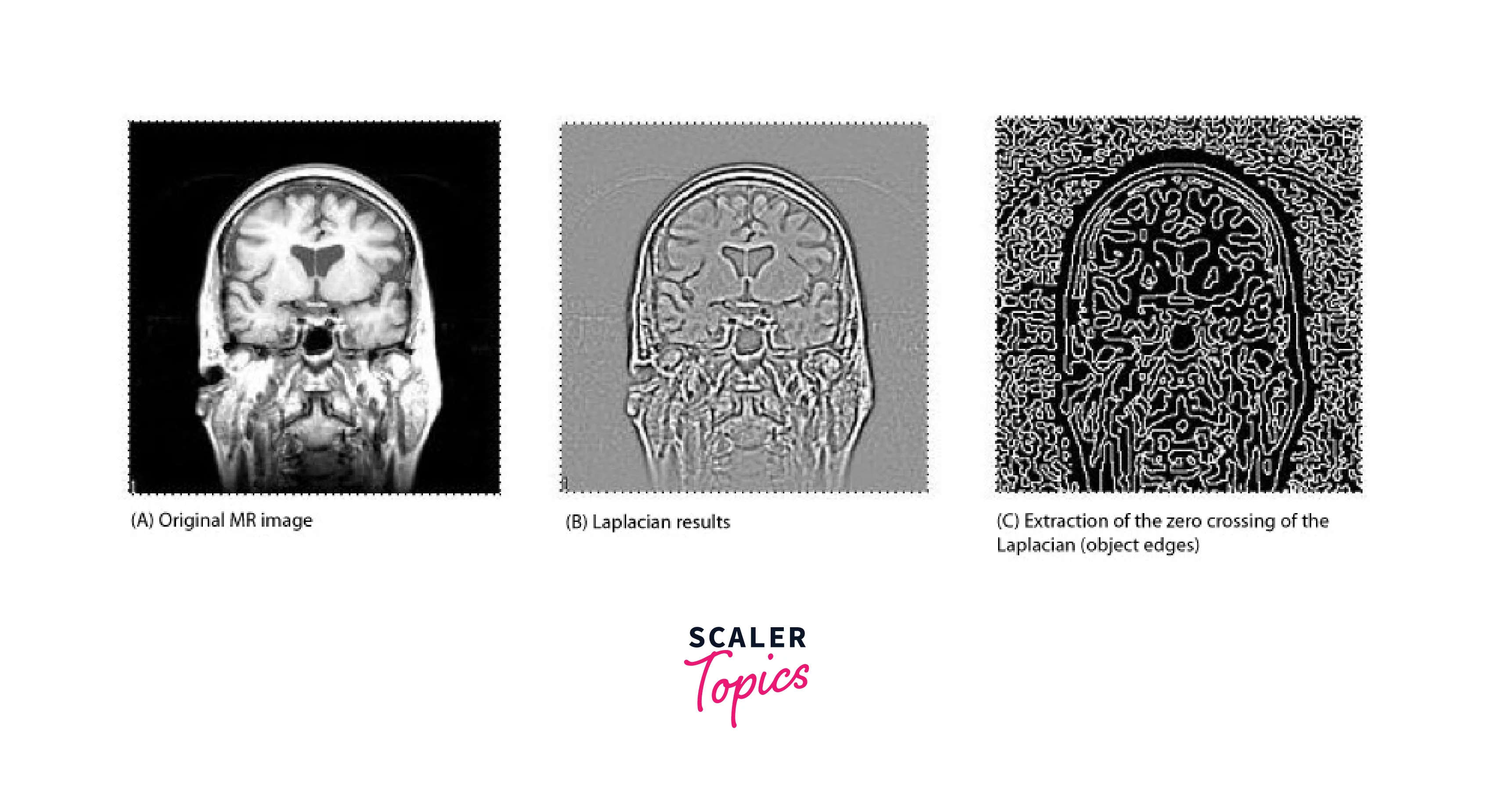
Laplacian Filter
The Laplacian filter is a linear filter that highlights edges in an image by computing the second derivative of the image intensity values. It is commonly used for edge detection and can be used in combination with other filters to enhance image features.
Mean Filter
The mean filter is a linear filter that smooths an image by replacing each pixel with the average of its neighboring pixels. It is commonly used to remove noise from images, but can also blur the image and reduce image detail.
Median Filter
The median filter is a non-linear filter that replaces each pixel with the median value of its local neighborhood. It is commonly used to remove salt and pepper noise from images while preserving image detail and sharpness.

Neighbourhood Average Filter
The neighborhood average filtering in image processing is a non-linear filter that replaces each pixel with the average value of its neighboring pixels. It can be used to smooth an image or remove noise but may blur image detail and reduce contrast.
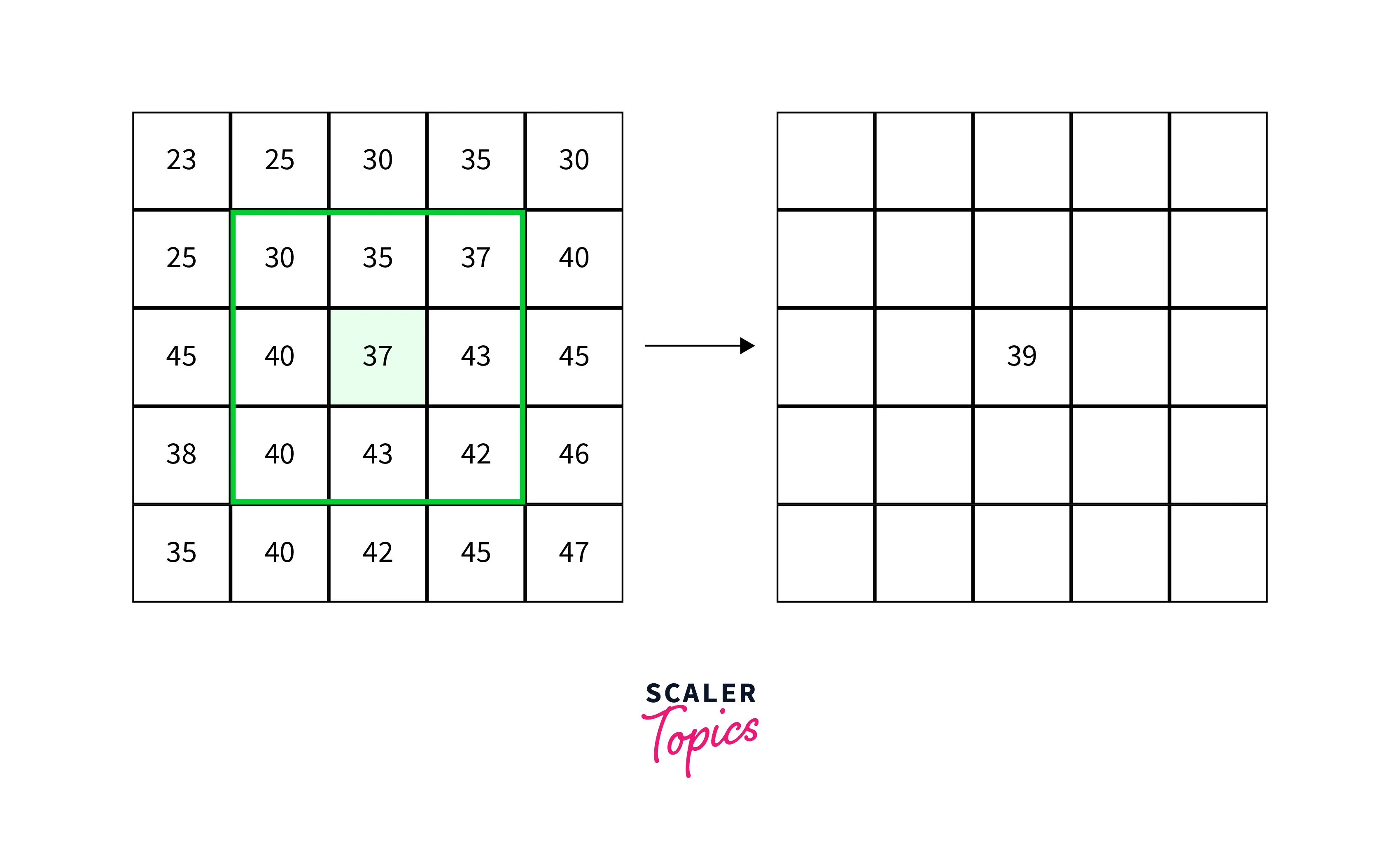
BOX Filter
The box filtering in image processing is a type of linear filter that smooths an image by replacing each pixel with the average value of its neighboring pixels within a rectangular kernel. It is one of the commonly used image processing filters to blur an image and remove noise, but can also reduce image detail and sharpness.

Gaussian Filter
Gaussian smoothing is a popular filtering in image processing technique used to reduce noise and blur an image by convolving it with a Gaussian kernel. This filter gives more weight to nearby pixels and less weight to distant pixels, creating a smoother and more natural-looking image. It is commonly used in computer vision, image processing, and signal processing applications.

Rotational Geometry
Rotational geometry plays an important role in image processing filters, particularly in the field of computer vision. It is used to analyze the rotational properties of objects in images, such as their orientation and symmetry. One common application is in object recognition, where the rotational properties of an object are used to distinguish it from other objects in the image.
Rotational geometry fro filtering in image processing can also be used to correct the image distortion caused by camera rotation or misalignment, such as in panoramic image stitching. In addition, rotational geometry is used in image registration, which involves aligning multiple images of the same scene taken from different viewpoints, by estimating their rotation and translation parameters.
Here is a sample Python code that uses OpenCV library to apply rotational geometry for filtering in image processing:
-
In this code, we first load the input image using the cv2.imread() function. We then define the center of rotation and the angle of rotation. In this example, we have defined the center of rotation as the center of the image, and the angle of rotation as 45 degrees.
-
After defining the center of rotation and the angle of rotation, we create the rotation matrix using the cv2.getRotationMatrix2D() function. This function takes the center of rotation, the angle of rotation, and the scaling factor as input, and returns the rotation matrix.
-
Finally, we apply the rotation matrix to the input image using the cv2.warpAffine() function. This function takes the input image, the rotation matrix, and the size of the output image as input, and returns the rotated image.
-
We then display the original and rotated images using the cv2.imshow() function and wait for the user to press any key to close the windows using the cv2.waitKey() and cv2.destroyAllWindows() functions.
Sample Output

Fourier Transform Property
The Fourier Transform is a mathematical tool used in signal processing and filtering in image processing to decompose a signal or image into its constituent frequencies. The Fourier Transform has several important properties that make it useful in the field of filtering in image processing.
One such property is the Fourier Transform Property, which states that the Fourier Transform of a convolution of two signals or images is equal to the product of their individual Fourier Transforms.
This property is particularly useful in the domain of filtering in image processing, where convolution is a common operation used to filter and enhance images. By applying the Fourier Transform to both the original image and the filter kernel, we can perform convolution in the frequency domain, which can be more efficient than performing convolution in the spatial domain.
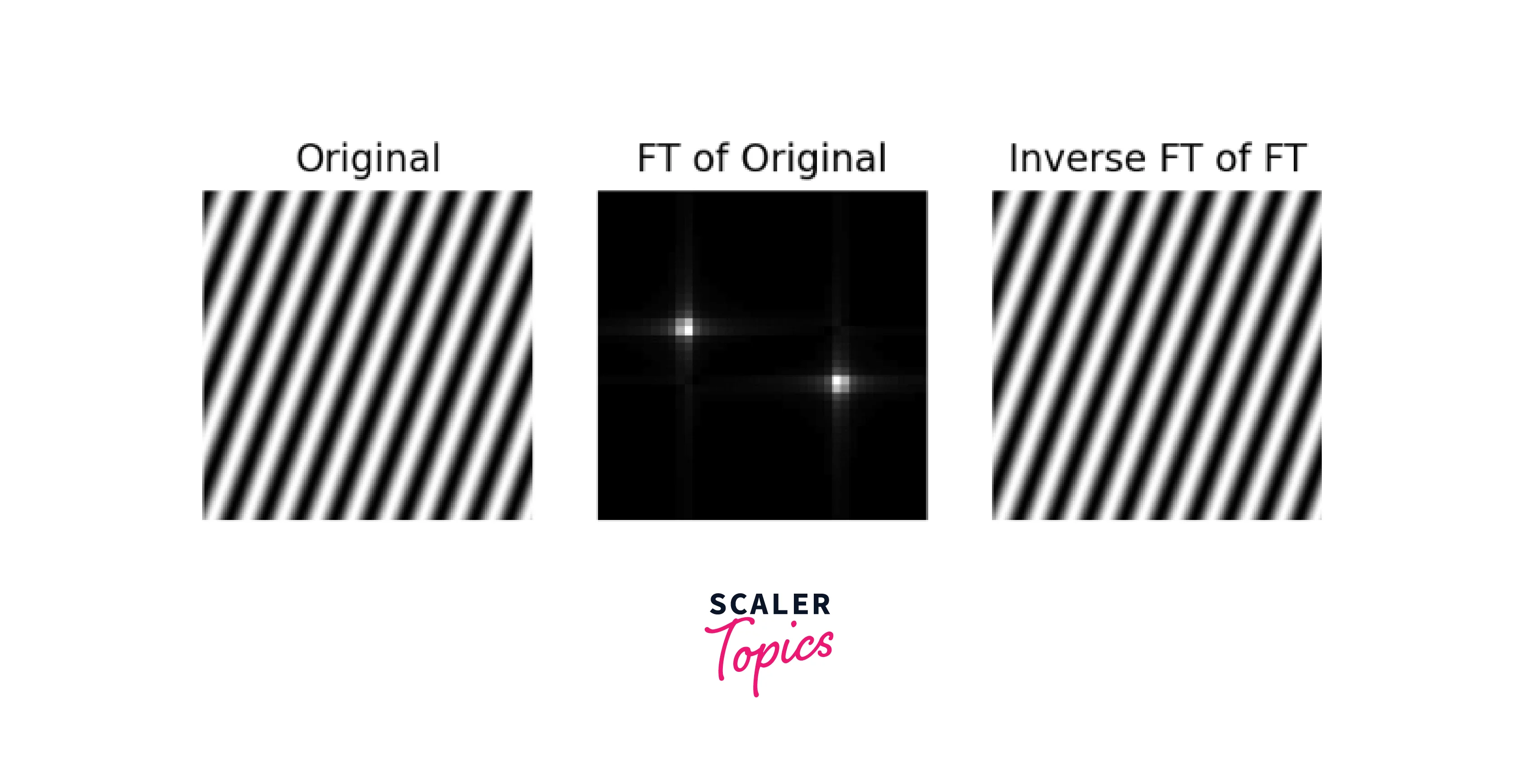
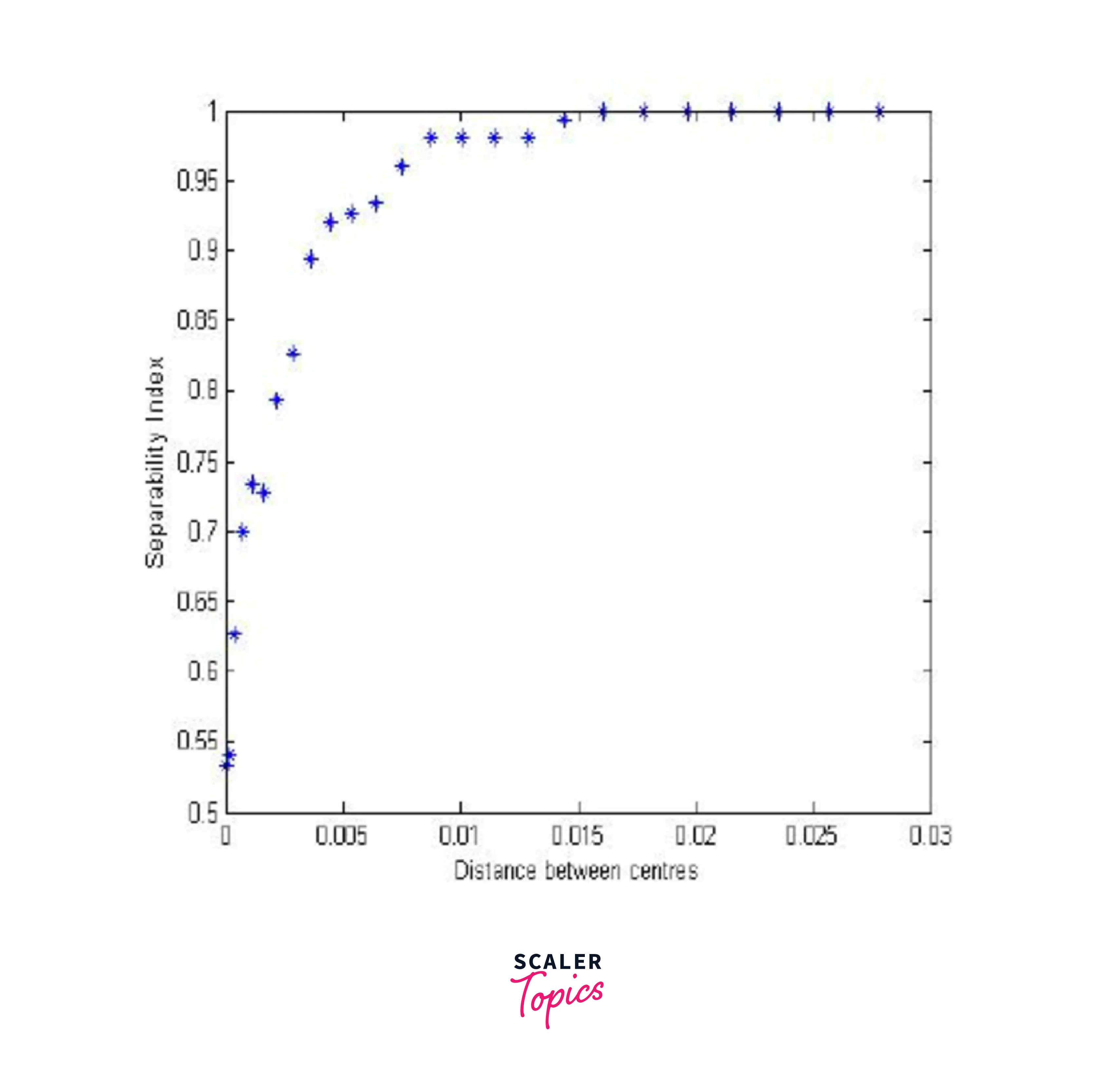
Gaussian Separability
Gaussian separability filtering in image processing refers to the property that a two-dimensional Gaussian kernel can be factored into two one-dimensional kernels, one in the horizontal direction and one in the vertical direction. This means that instead of convolving the image with a two-dimensional Gaussian kernel, we can convolve it with two one-dimensional Gaussian kernels, one in the horizontal direction and one in the vertical direction. This reduces the number of computations required, making the filtering process faster.
Cascading Gaussians
Cascading Gaussians refers to the process of applying multiple Gaussian filtering in image processing in succession to an input signal or image. The purpose of cascading Gaussian filters is to achieve a more refined and accurate output by removing noise and small details. Each filter in the cascade will have a different level of smoothing, with the first filter typically having a higher level of smoothing than the subsequent filters. Cascading Gaussian filters are commonly used for filtering in image processing, computer vision, and signal processing applications.
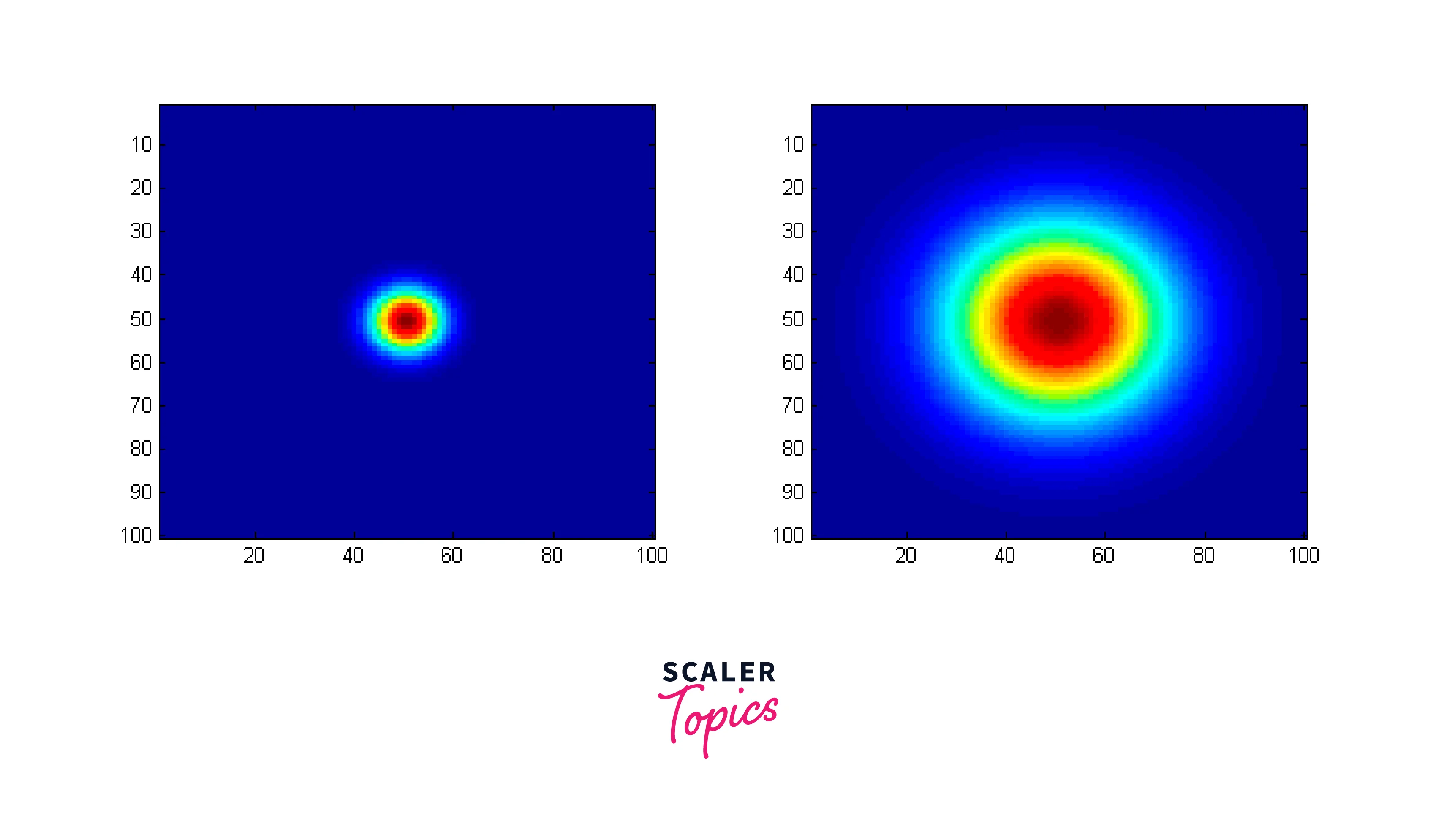
Designing Gaussian Filters
Gaussian filters are widely used in signal processing and filtering in image processing applications to remove noise and blur the image. Designing a Gaussian filter involves selecting the appropriate filter size and determining the value of the standard deviation of the Gaussian distribution. The standard deviation determines the degree of smoothing, with a higher value resulting in more smoothing. The filter size will affect the extent of the Gaussian distribution, with a larger filter size leading to a broader distribution. In general, designing a Gaussian filter involves finding the balance between smoothing and preserving details in the signal or image.
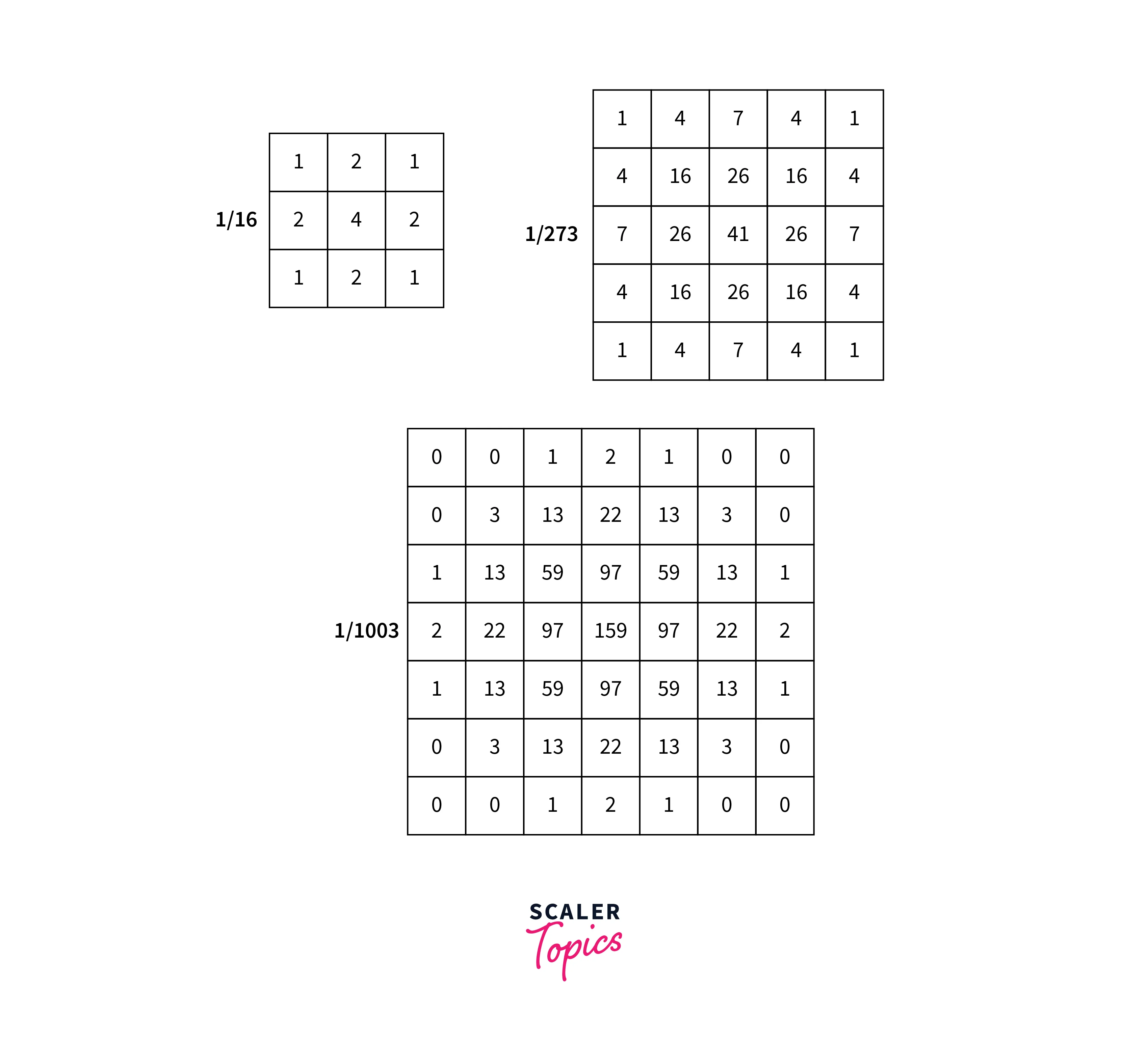
Discrete Gaussian Filters
Discrete Gaussian filters refer to a family of filters that approximate the continuous Gaussian function with a discrete kernel. These filters are commonly used in digital image processing and signal processing applications, where the input signal is discrete.
The discrete Gaussian filter can be implemented using a convolution operation, where the filter kernel is convolved with the input signal. The size of the filter kernel and the value of the standard deviation determine the degree of smoothing. Discrete Gaussian filters have several properties that make them popular, including isotropy, linearity, and shift-invariance.
Conclusion
- In conclusion, filtering in image processing is an essential process that helps remove noise, enhance features, and improve image quality.
- Gaussian filters, including cascading Gaussians and discrete Gaussian filters, are widely used in image filtering due to their effectiveness and simplicity.
- Appropriate design and implementation of these filters are crucial for achieving the desired image filtering results.
