October 7, 2024

Find Duplicates in Array

Problem Statement

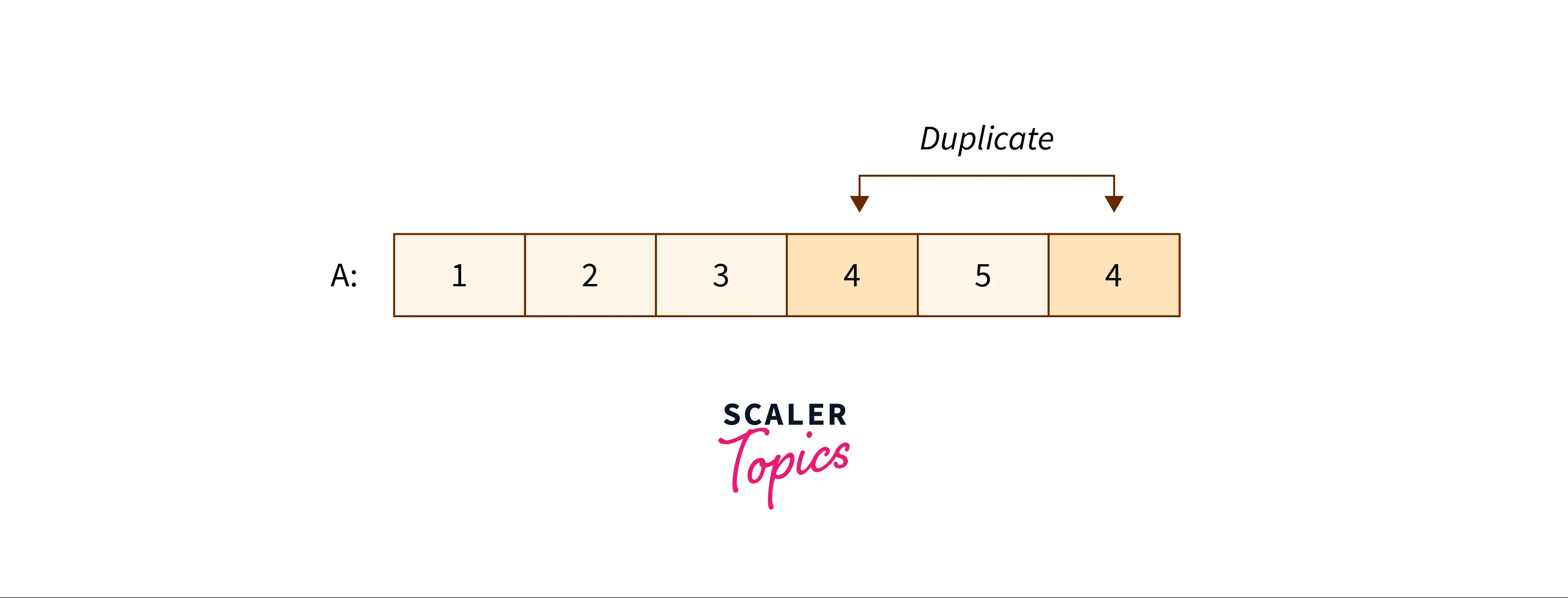
Given an array A of size N + 1. Each element in array A is between 1 and N. Write a program to find one of the duplicates in array A. If there are multiple answers, then print any.

Example 1

Input:
N = 5
A = [1, 2, 5, 3, 4, 3]
Output
3

Explanation
In this example, element 3 is repeated at position 4 and position 6 in array A.

Example 2

Input
N = 5
A = [1, 2, 4, 2, 4, 4]
Output
2

Explanation
In this example, element 2 is repeated as well as element 4 is repeated. Hence we can output any of them.

Constraints

$1 <= N <= 10^{5}$

$1 <= A [i] <= N$

Problem Discussion

Before moving on to the solution, let us first analyze the constraints.
In this problem, we are given that $N$ is at least $1$ . This means that the size of the input array will be at least 2. This constraint guarantees that there is at least one duplicate element in the array. Why?

This is because we are given that array $A$ is of size $N + 1$ and each element $A [i]$ is between $1$ and $N$ . So, if we give unique values to the first $N$ positions in the array $A$ , then the last position of array $A$ will be a duplicate in the array.

For example:
$N = 6$
Then, the maximum number of unique values in $A$ can be $5$ .
$A = [1, 2, 3, 4, 5, 4]$ . The last element will be repeated. So the answer always exists.

Approach 1: Brute Force

We can solve this problem using a simple brute force over the array $A$ . We can use two nested iterations over array $A$ to find the duplicate element.

For each element $A [i]$ , we can check is there an element $A [j]$ such that $i \neq j$ and $A [i] == A [j]$ .
If such an element $A [j]$ exists, then we can say that $A [i]$ is the repeated element and we have found our answer.
In this way, we can find duplicate in array.

C++ Implementation

#include <bits/stdc++.h> 
using namespace std;

int findDuplicate(vector<int> &arr, int length){
    int duplicate = -1;
    for(int i = 0; i < length; i ++) {
        // Iterate over all arr[i].
        for(int j = i + 1; j < length; j ++) {
            // For each arr[i], consider all elements arr[j].
            // We iterate from j = i + 1, so this guarantees that i != j.
            if(arr[i] == arr[j]) {
                duplicate = arr[i];
                break;
            }
        }
        if(duplicate != -1) break;
    }
    return duplicate;
}

Java Implementation

import java.util.* ;

public class FindDuplicate{
    public static int findDuplicate(ArrayList<Integer> arr, int length){
        int duplicate = -1;
        for(int i = 0; i < length; i ++) {
            // Iterate for all arr[i].
            for(int j = i + 1; j < length; j ++) {
                // For each arr[i], consider all elements arr[j].
                // We iterate from j = i + 1, so this guarantees that i != j.
                if(arr.get(i) == arr.get(j)) {
                    duplicate = arr.get(i);
                    break;
                }
            }
            if(duplicate != -1) break;
        }
        return duplicate;
    }
}

Python3 Implementation

def findDuplicate(arr:list, length:int):
    duplicate = -1
    for i in range(0, length):
        for j in range(i + 1, length):
            # For each arr[i], consider all elements arr[j].
            # We iterate from j = i + 1, so this guarantees that i != j.
            if arr[i] == arr[j]:
                duplicate = arr[i]
                break
        if duplicate != -1:
            break
    return duplicate

Time Complexity Analysis

In this method, we will do two nested iterations over the array $A$ of size $N + 1$ . Hence the time complexity will be $O (N)$ for the outer loop and $O (N)$ for the inner loop. Since the iterations are nested, the time complexity will be $O (N^{2})$ .

Time complexity: $O (N^{2})$

Space Complexity Analysis

In this method, we only need a constant amount of variables of iteration. We are also keeping another variable to store the duplicate element. Hence the space complexity is $O (1)$ .

Space Complexity: $O (1)$

:::

:::section{.main}

Approach 2: Using Sorting

Firstly, we will sort the given array A in increasing or decreasing order. This will guarantee that all equal elements are placed side by side in the sorted array.
After sorting, equal elements will be placed one after the other so we can do a simple iteration on the sorted array A and check adjacent elements.
When iterating over the array, if we find a position where adjacent elements are equal, then we have found our duplicate element.

For example
$A : [3, 2, 5, 4, 3, 1, 4]$
$S o r t e d (A) : [1, 2, 3, 3, 4, 4, 5]$
Now if we iterate over the sorted array $A$ , and compare adjacent elements at position $3$ , we will find that $A [3] = A [4] = 3$ .
This means that the duplicate element is $3$ .

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

int findDuplicate(vector<int> &arr, int length){
    // Sort the array A in increasing order.
    sort(arr.begin(), arr.end());

    int duplicate = -1;
    for(int i = 0; i + 1 < length; i ++) {
        // Compare adjacent elements. 
        if(arr[i] == arr[i + 1]) {
            /* If adjancent elements are equal, 
             then we have found the duplicate element. */
            duplicate = arr[i];
            break;
        }
    }
    return duplicate;
}

Java Implementation

import java.util.* ;

class FindDuplicate {
    public static int findDuplicate(ArrayList<Integer> arr, int length){
        // Use Collections.sort as it works in O(N log(N)) time.
        Collections.sort(arr);
        int duplicate = -1;
        for(int i = 0; i + 1 < length; i ++) {
            // Compare adjacent elements.
            if(arr.get(i) == arr.get(i + 1)) {
                /* If adjancent elements are equal, 
                 then we have found the duplicate element. */
                duplicate = arr.get(i);
                break;
            }
        }
        return duplicate;
    }
}

Python3 Implementation

def findDuplicate(arr:list, length:int):
    duplicate = -1
    # Sort list in ascending order to group equal elements.
    arr.sort()
    for i in range(0, length - 1):
         # Iterate over list arr and compare adjancet elements.
        if arr[i] == arr[i + 1]:
            # If adjancent elements are equal, 
            # then we have found the duplicate.
            duplicate = arr[i]
            break
    return duplicate

Time Complexity Analysis

We can sort the array using a comparison-based sorting algorithm. This will take $O (N l o g (N))$ time. Now to search for the duplicate element, we are doing a simple iteration. This will take $O (N)$ time.

Time complexity: $O (N l o g (N))$ .

We can also use a linear time sorting algorithm like Counting sort. In this case, the time complexity will be $O (N)$ . The trade-off here is that counting sort requires extra space.

Space Complexity Analysis

We are not using any extra space in our algorithm. We only need a constant number of variables for iteration and searching for the answer. Hence the space complexity is $O (1)$ .
Space Complexity: $O (1)$

If we use a linear time sorting algorithm like counting sort, then the space complexity will be $O (N)$ as it requires an extra array to store the count of each element.

Approach 3: Using Frequency Array

To find a duplicate element in the array, we can make use of the observation that any duplicate number A[i] will occur more than once in array A. This means that suppose, if we know the number of times each element occurs in array A, then the duplicate element will be one of the elements whose frequency or the number of times it occurs in A is more than one.

Now how to find the frequency of each element ?
To do this, we can create a frequency table over the array A.
A frequency table is a map that represents the number of times each element occurs in array A. It represents the count or frequency of each element in array A.

A frequency table can be implemented using arrays or a hash map. Generally, if the range of elements in the given array A is small, then it is preferred that we use arrays as a frequency table. This is because a hash map can have some overhead costs associated with it.
Let’s say we have a variable $f r e q$ that represents our frequency table of size $N$ . We will create a table of size $N$ as $A [i]$ lies between $1$ and $N$ .
Now, we iterate over array A and increment $f r e q [A [i]]$ by $1$ . In this way, we can build the frequency table.
Now, we can simply check the frequency table. If at any point $f r e q [i] > 1$ then we have found the duplicate element equal to $i$ .

For example,
Let us take $A = [3, 2, 5, 4, 3, 1, 4]$
Now we build a frequency table $f r e q = [0, 1, 1, 2, 2, 1]$
It means $f r e q [0] = 0, f r e q [1] = 1, f r e q [2] = 1, f r e q [3] = 2$ and so on.
As we can see the $f r e q [3] = 2$ and $f r e q [4] = 2$ , so both these elements are repeated. We can output any one of them as both are duplicates in the array.

C++ Implementation

#include <bits/stdc++.h> 
using namespace std;

int findDuplicate(vector<int> &arr, int length){
    int duplicate = -1;
    // Range of arr[i] = [1, length - 1]
    // Create a frequency array of size length.
    // frequency[i] = Number of times i occurs in A.
    vector<int> frequency(length, 0);
    for(int x : arr) {
        // For each element x, increment frequency[x] by 1.
        frequency[x] += 1;
    }
    for(int x : arr) {
        // Iterate over frequency array where frequency[x] > 0.
        if(frequency[x] > 1) {
            // Now if frequency[x] > 1, then x is a duplicate.
            duplicate = x;
            break;
        }
    }
    return duplicate;
}

Java Implementation

import java.util.* ;

public class FindDuplicate{
    public static int findDuplicate(ArrayList<Integer> arr, int length){
        int duplicate = -1;
        // Range of arr[i] = [1, length - 1]
        // Create a frequency array of size length.
        // frequency[i] = Number of times i occurs in A.
        int frequency[] = new int[length];
        for(int x : arr) {
            // For each element x, increment frequency[x] by 1.
            frequency[x] += 1;
        }
        for(int x : arr) {
            // Iterate over frequency array where frequency[x] > 0.
            if(frequency[x] > 1) {
                // Now if frequency[x] > 1, then x is a duplicate.
                duplicate = x;
                break;
            }
        }
        return duplicate;
    }
}

Python3 Implementation

def findDuplicate(arr:list, length:int):
    duplicate = -1
    # Range of arr[i] = [1, length - 1]
    # Create a frequency list of size length.
    # frequency[i] = Number of times i occurs in A.
    frequency = [0] * length
    for i in arr:
        # For each element x, increment frequency[x] by 1.
        frequency[i] += 1
    for i in arr:
        # Iterate over frequency array where frequency[x] > 0.
        if frequency[i] > 1:
            # Now if frequency[x] > 1, then x is a duplicate.
            duplicate = i
            break
    return duplicate

Time Complexity Analysis

To create the frequency table, we need to do an iteration over the array $A$ . This will take $O (N)$ time. To find the duplicate element, we need to do an iteration over the frequency array. The size of the frequency array is also bounded by $O (N)$ , hence the time taken will be $O (N)$ .

Time complexity: $O (N)$

Space Complexity Analysis

In this method, we need to create a frequency array of size $N + 1$ . So, the space complexity for this algorithm is $O (N)$ .

Space complexity: $O (N)$

Approach 4: Linked List Cycle Method

This method considers the array as a linked list. Suppose we consider the given elements of the array as nodes of a linked list. Here the $i n d e x$ of the element indicates the address of the node and it points to node $A [i n d e x]$ . $A [i n d e x]$ stores the address of the next node in the linked list. For example, consider the below array $A : [1, 2, 3, 4]$
In this case, we have 4 linked lists, each of size 1.

Consider another example $A : [2, 3, 1, 5, 4]$

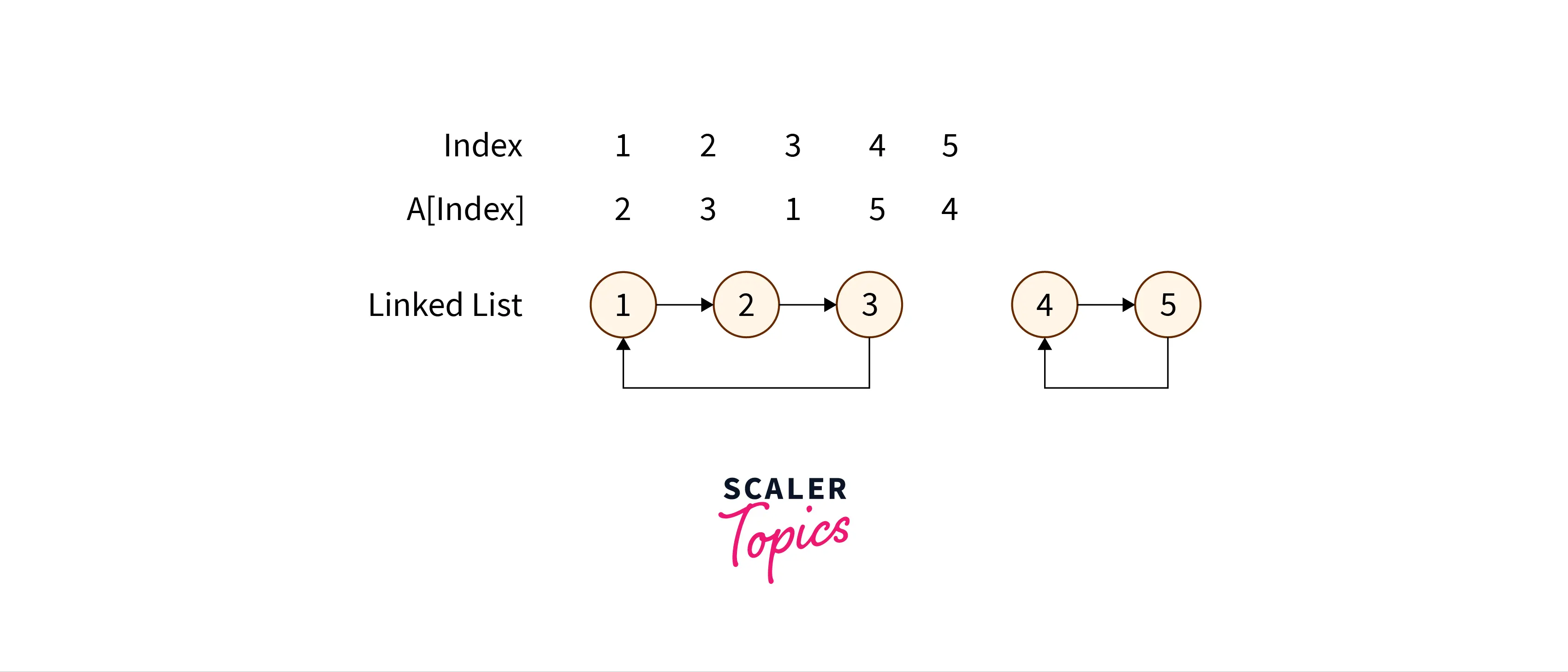
duplicate-array-by-linked-list-cycle-method

In this way, we represent each list A in the form of a linked list.
In the examples shown above, there are no duplicate elements in array A. Observe that, this means that each element occurs only once so there can be at most one incoming connection for each node. Try out some more examples to understand this clearly.

Now suppose, we add a duplicate element in array A. The main observation is that there will be at least one node in the linked list that will have multiple incoming connections. This is because there are at least two distinct positions i and j such that $A [i] = A [j]$ . So nodes $i$ and $j$ will point to the same node and that node will have multiple incoming connections.

To find the duplicate element, we will represent array A in the form of a linked list.
Now, to find the duplicate element, we need to find the start of the cycle. This can be done using Floyd’s cycle finding algorithm (discussed below).

Let us understand this using an example.
Consider $A = [3, 2, 4, 1, 5, 1]$
Let us say, we are index $0$ , $A [0] = 3$ , so the next element is at index $3$ .
At index $3$ , $A [3] = 1$ , so the next element of the list is at index $1$ .
At index $1$ , we have $A [1] = 2$ , so the next element of the list is at index $2$ .
At index $2$ , we have $A [2] = 4$ , so the next element is at index $4$ .
At index $4$ , we have $A [4] = 5$ , so the next element is at index $1$ .

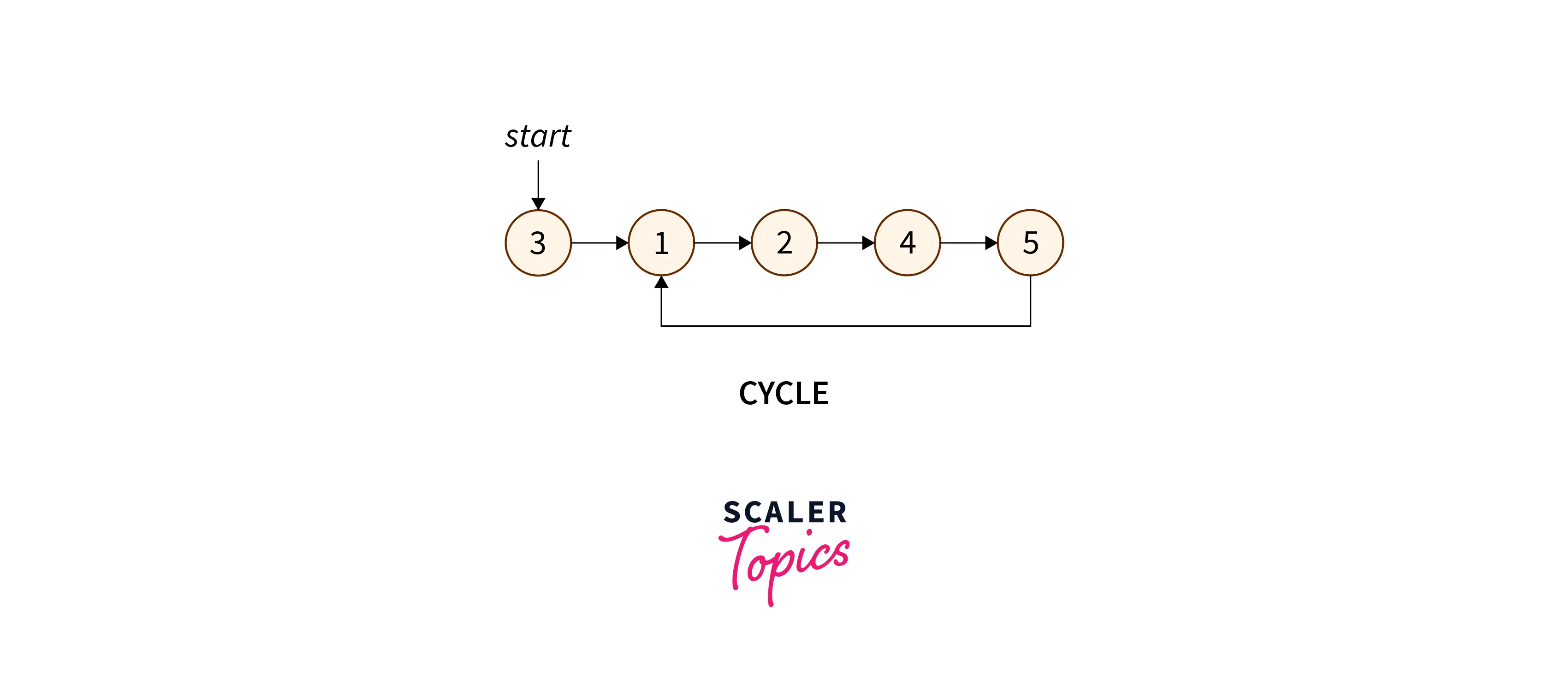
Now as we can see this represents a linked list structure with a cycle. So when the elements range between $1$ and $N$ and there is a duplicate then it will form a cycle.
The duplicate element will be the start of this cycle. This is because the duplicate element will point to an element that has already been visited. So, if we find the start of this cycle, then we can find the duplicate in array $A$ .

Now to find the start of the cycle, we can use Floyd’s cycle finding algorithm.
The idea is to use two pointers – slow and fast pointer. We will start from index $0$ and keep on moving the slow and the fast pointer. The slow pointer will move by one step and the fast pointer will move by two steps. Now when these pointers meet we can say that both the pointers are in the cycle.

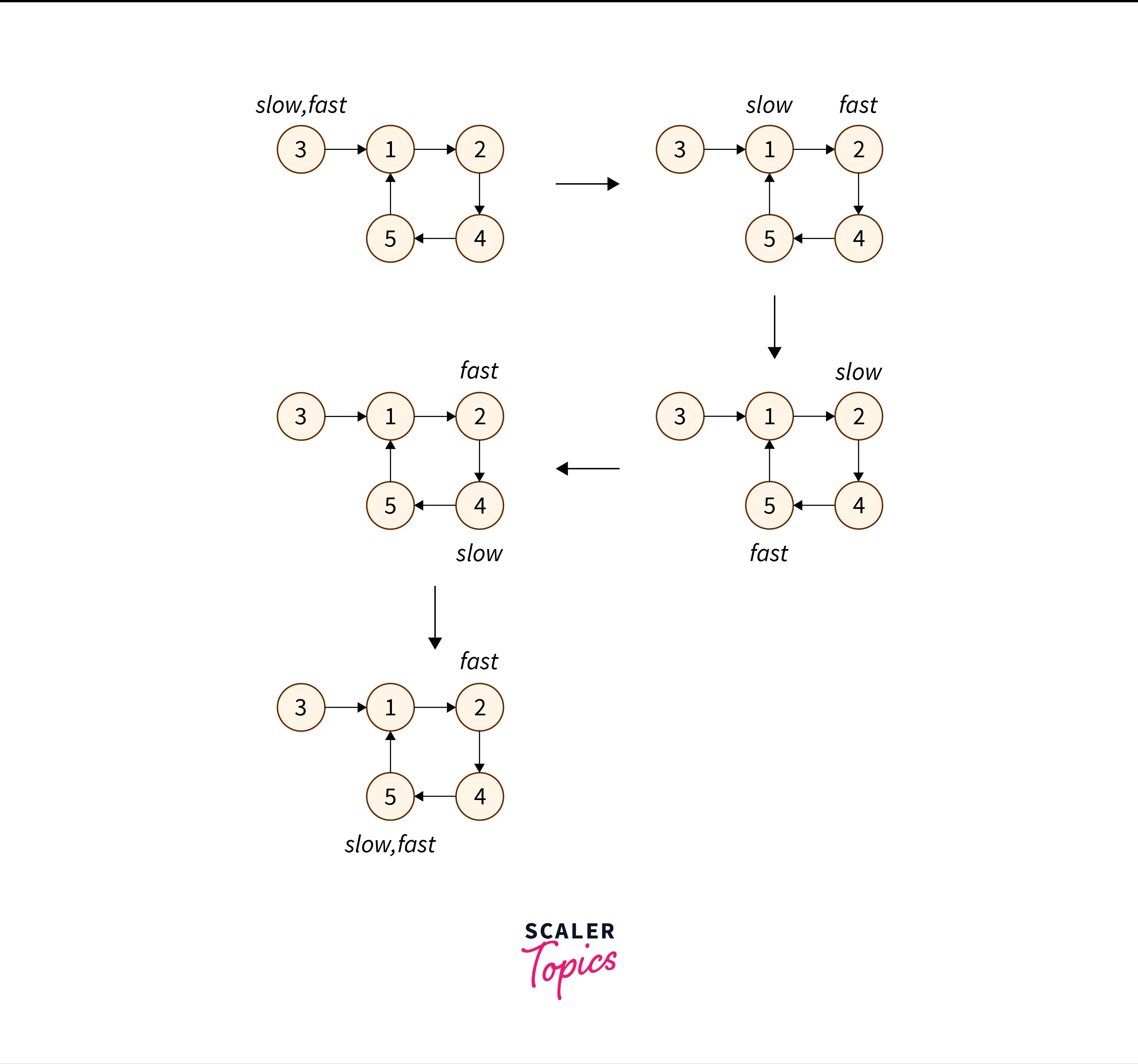
duplicate-floyds-cycle-finding-algorithm

To find the start of the cycle, we will re-initialize the slow pointer to $0$ and this time, we will update both the pointers by one step at a time. Now, these pointers will end up meeting at the start of the linked list. In this way, we can find the duplicate.

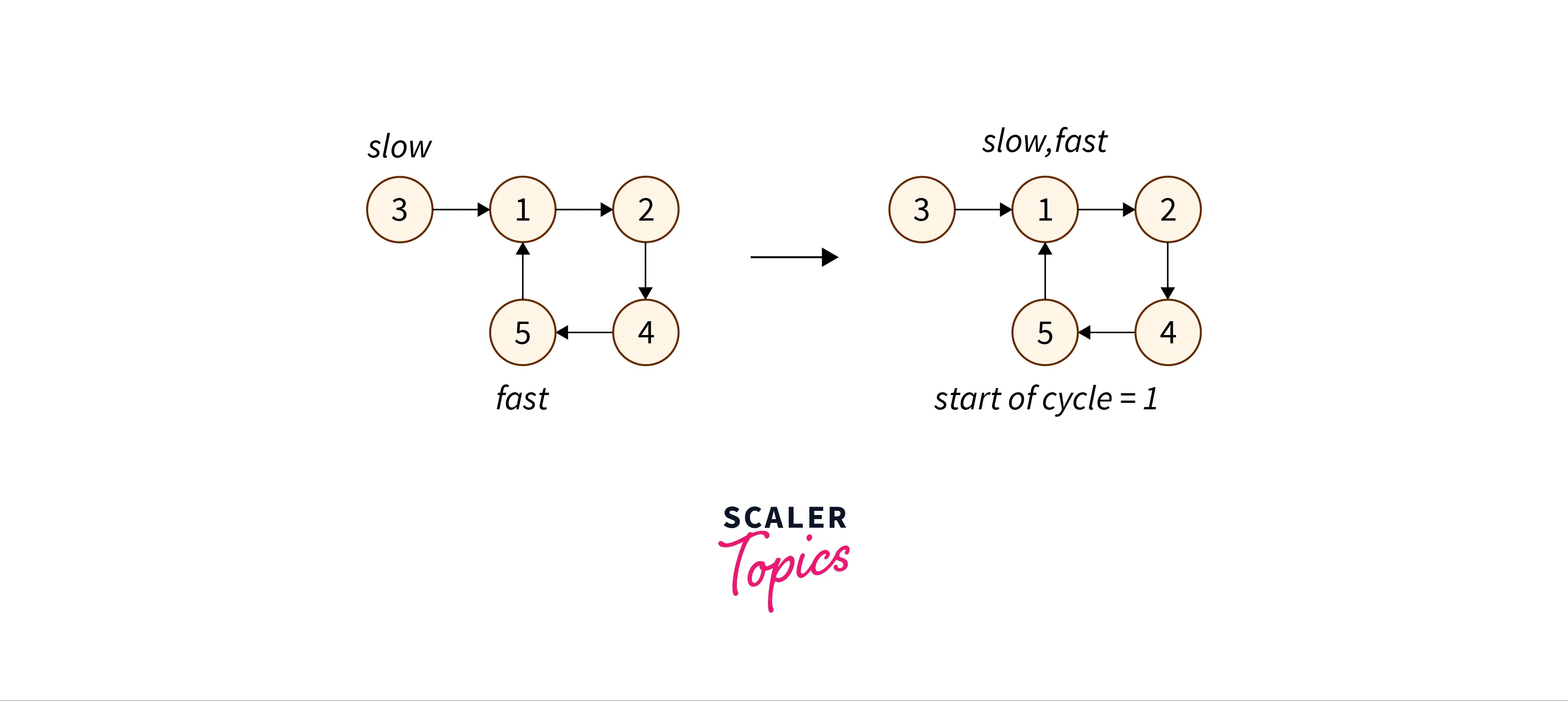
Now, the question is why should slow and fast pointers meet at the start of the cycle using this method. To understand this consider the image below.

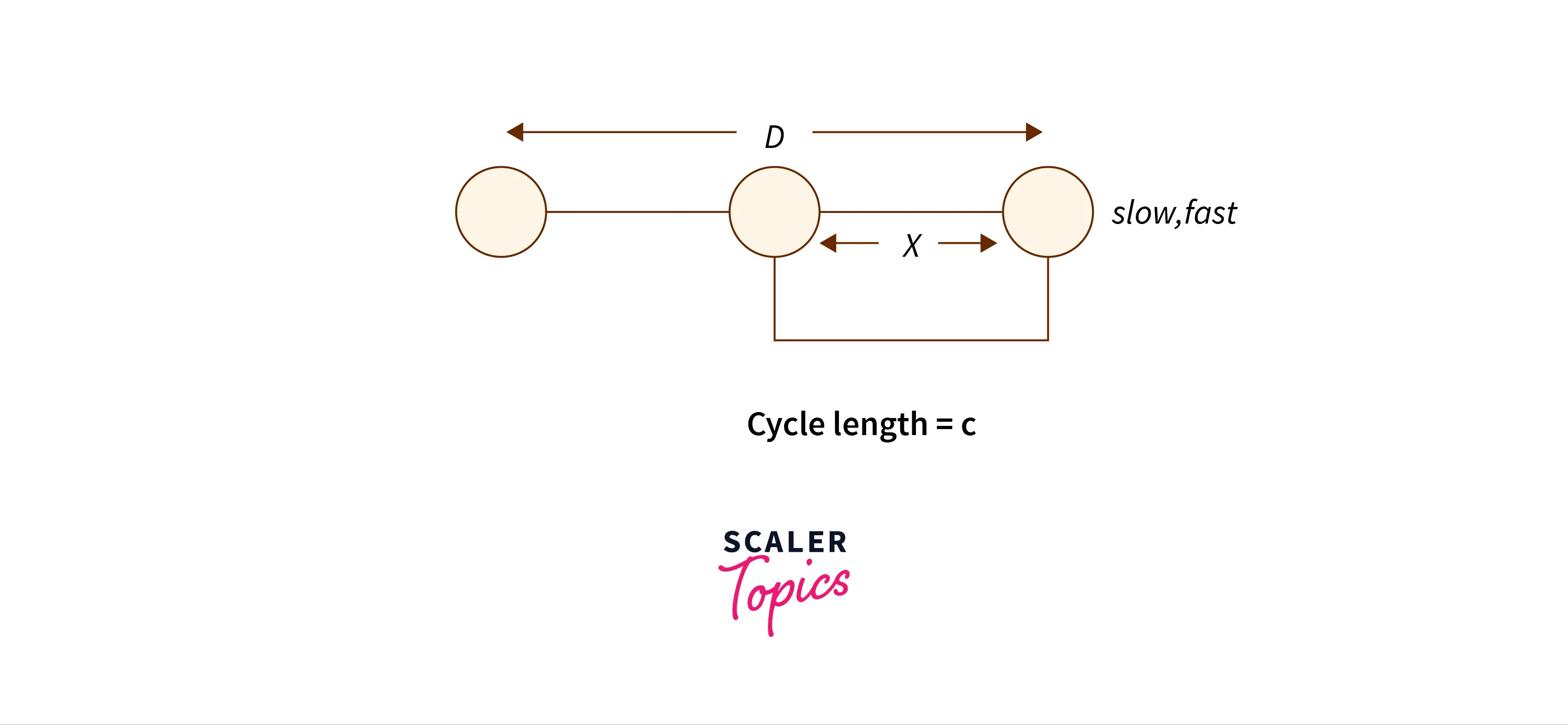
Let us say:
The distance between the first element and the point of collision of the slow and the fast pointer is $D$ .
Cycle length = $C$ and the Distance of the point of collision from the start of the cycle is $X$ .
Distance traveled by slow pointer = $D$ so the distance traveled by fast pointer = $2 D$ .
If slow and fast pointers meet, then the distance between them is integer multiple of $C$ .
This means $D = k * C$ , where $k$ is some positive constant.
Now when we reset the slow pointer, the fast pointer has moved a distance of X from starting point of the cycle.
If we now update both the pointers, one at a time, this means that the slow pointer will travel a distance of $(D - X)$ and the fast pointer will also travel a distance of $D - X$ to meet the slow pointer at the start of the cycle.
In this way, we can find the duplicate element in the array.

C++ Implementation

#include <bits/stdc++.h> 
using namespace std;

int findDuplicate(vector<int> &arr, int length){
    int slow = arr[0];
    int fast = arr[arr[0]];

    while (fast != slow) {
        // slow increases by 1. fast increases by 2.
        slow = arr[slow];
        fast = arr[arr[fast]];
    }
    // Re-initialize slow to 0 and increase both slow and fast by 1.
    slow = 0;
    while (fast != slow) {
        slow = arr[slow];
        fast = arr[fast];
    }
    // Duplicate = Start of cycle = slow
    return slow;
}

Java Implementation

import java.util.* ;

public class FindDuplicate{
    public static int findDuplicate(ArrayList<Integer> arr, int length){
        int slow = arr.get(0);
        int fast = arr.get(arr.get(0));

        while (fast != slow) {
            // slow increases by 1. fast increases by 2.
            slow = arr.get(slow);
            fast = arr.get(arr.get(fast));
        }
        // Re-initialize slow to 0 and increase both slow and fast by 1.
        slow = 0;
        while (fast != slow) {
            slow = arr.get(slow);
            fast = arr.get(fast);
        }
        // Duplicate = Start of cycle = slow
        return slow;
    }
}

Python3 Implementation

def findDuplicate(arr:list, length:int):
    slow, fast = arr[0], arr[arr[0]]

    while fast != slow:
        # slow increases by 1. fast increases by 2.
        slow = arr[slow]
        fast = arr[arr[fast]]
    # Re-initialize slow to 0 and increase both slow and fast by 1.
    slow = 0;
    while fast != slow:
        slow = arr[slow]
        fast = arr[fast]
    # Duplicate = Start of cycle = slow
    return slow;

Time Complexity Analysis

To find the cycle, we will iterate over the cycle once. This is true because when both the pointers – slow and fast are in the cycle, the distance between them will decrease by $1$ . Since the cycle length is $O (N)$ the time taken to find the cycle is $O (N)$ . To find the starting point of the cycle, we will iterate over the array once. The time complexity of this algorithm is $O (N)$ .

Time complexity: $O (N)$

Space Complexity Analysis

If we look at the implementation, we are only using a constant amount of space. Hence the space complexity is $O (1)$ .

Space complexity: $O (1)$

Approach 5: Binary Search on Array

Suppose, we are given that there is only one duplicate element in array $A$ . This means that there are $N$ unique elements in array $A$ and one duplicate element. We can use binary search to find the duplicate element.

The idea is to perform a binary search to find the duplicate element in the range $[1, N]$ . Given the middle element of the range, we will count the number of elements smaller than or equal to the middle element.
If $l o w = 1$ , $h i g h = N$ and $m i d = (l o w + h i g h) / 2$ .
Then if $c o u n t$ represents number of $A [i] <= m i d$ .
There are three cases.

If the $c o u n t$ is greater than $m i d$ , then in this case we have a smaller subproblem of the original problem. Observe that, in this case, we can choose a subset of all elements that are smaller than or equal to $m i d$ , but the size will be greater than $m i d$ . So, it is like we have an array of size $K (= m i d)$ with elements in the range $[1, K]$ , and the size is at least $K + 1$ . So this is a smaller subproblem of the original problem. We will shift our $h i g h$ to $m i d$ .
If the $c o u n t$ is equal to $m i d$ , then, in this case, we can say that there are no duplicates less than or equal to $m i d$ . This is because we have only one duplicate element and $N$ unique elements, so elements from $1$ to $m i d$ will always get counted. So we can discard half the possibilities so we shift our $l o w$ to $m i d + 1$ .
The case where the $c o u n t$ is less than $m i d$ is not possible. This is because $m i d$ lies between $l o w$ and $h i g h$ and there is one duplicate element in $A$ . This implies we have $N$ unique elements from $1$ to $N$ so no matter what the value of mid is, the elements from $1$ to $m i d$ will always be counted.

Let us take an example to understand this.
Let us say $A = [3, 2, 4, 1, 5, 2]$

$L o w = 1, h i g h = 6, m i d = 3 => c o u n t = 4$ (as 4 elements $[3, 2, 1, 2]$ are less than or equal to 3 in the A)
$L o w = 1, h i g h = 3, m i d = 2 => c o u n t = 3$ (as 3 elements $[2, 1, 2]$ are less than or equal to 2 in A)
$L o w = 1, h i g h = 2, m i d = 1 => c o u n t = 1$ so we set low = mid
$L o w = 2, h i g h = 2$ . Since both are equal we have found our answer and we terminate the loop.
To find the number of elements that are less than or equal to a given value of $m i d$ , we can do a simple iteration over $A$ and count such elements.

C++ Implementation

#include <bits/stdc++.h> 
using namespace std;

int findDuplicate(vector<int> &arr, int length){
    int low = 1, high = length - 1;
    while(low < high) {
        // Find mid element.
        int mid = low + (high - low)/2;
        int count = 0;
        // Count the number of elements in A smaller than or equal to mid.
        for(int x : arr) {
            if(x <= mid) count ++;
        }
        if(count > mid) {
            // In this case, at least duplicate lies in the range [1, mid].
            high = mid;
        }
        else {
            // In this case, at least one duplicate lies in the range [mid + 1, high].
            low = mid + 1;
        }
    }
    return low;
}

Java Implementation

import java.util.* ;

public class FindDuplicate{
    public static int findDuplicate(ArrayList<Integer> arr, int length){
        int low = 1, high = length - 1;
        while(low < high) {
            // Find mid element.
            int mid = low + (high - low)/2;
            int count = 0;
            for(int x : arr) {
                // Count #elements smaller than or equal to mid.
                if(x <= mid) count ++;
            }
            if(count > mid) {
                // This means duplicate lies towards left range.
                high = mid;
            }
            else {
                // This means duplicate lies towards right range.
                low = mid + 1;
            }
        }
        return low;
    }
}

Python3 Implementation

def findDuplicate(arr:list, length:int):
    low, high = 0, length - 1
    while low < high:
        # Find mid element.
        mid = low + (high - low) // 2
        count = 0
        # Count #elements smaller than or equal to mid.
        for x in arr:
            if x <= mid:
                count += 1
        if count > mid:
            # This means duplicate lies towards left range.
            high = mid
        else:
            # This means duplicate lies towards right range.
            low = mid + 1
    return low

Time Complexity Analysis

In this method, we perform a binary search over array $A$ . For each iteration of binary search, we have to iterate over array $A$ to find the number of elements less than or equal to the given mid. Hence the time complexity is $O (N l o g (N))$ .

Time Complexity: $O (N l o g (N))$

Space Complexity Analysis

Binary search does not require any extra space. We use only a constant amount of space. Hence space complexity: $O (1)$

Approach 6: Count Iterations

In this method, the idea is to count the number of times, each element occurs while iterating over the array $A$ . This method relies on the fact that the frequency of duplicate elements is greater than one. In this method, we will find the duplicate element in a single pass.

We will maintain a frequency table count with all entries as $0$ .
Now iterate over the array A and for each element $A [i]$ increment $A [i]$ by $1$ . While iterating, if at any point, the number of occurrences of $A [i]$ is greater than $1$ , then we have found the duplicate element.

Example:
$A = [3, 2, 1, 4, 1, 5]$ $c o u n t = [0, 0, 0, 0, 0, 0, 0]$
Iteration 1: $c o u n t = [0, 0, 0, 1, 0, 0, 0]$ $c o u n t [A [1]] = c o u n t [3] = 1$ , so we continue.
Iteration 2: $c o u n t = [0, 0, 1, 1, 0, 0, 0]$ $c o u n t [A [2]] = c o u n t [2] = 1$ , so we continue.
Iteration 3: $c o u n t = [0, 1, 1, 1, 0, 0, 0]$ $c o u n t [A [3]] = c o u n t [1] = 1$ , so we continue.
Iteration 4: $c o u n t = [0, 1, 1, 1, 1, 0, 0]$ $c o u n t [A [4]] = c o u n t [4] = 1$ , so we continue.
Iteration 5: $c o u n t = [0, 2, 1, 1, 1, 0, 0]$ $c o u n t [A [1]] = c o u n t [1] = 2 (> 1)$ . We will break here because we have found a duplicate element.

C++ Implementation

#include <bits/stdc++.h> 
using namespace std;

int findDuplicate(vector<int> &arr, int length){
    int duplicate = -1;
    // Create a frequency table count of size length.
    // count[i] = Frequency of i in arr.
    vector<int> count(length, 0);
    for (int i = 0; i < length; i++) {
        // For each element arr[i], increment count[arr[i]] by 1.
        int x = arr[i];
        count[x] ++;
        if (count[x] > 1) {
            // If count[arr[i]] > 1, then we have found the duplicate element.
            duplicate = x;
            break;
        }
    }
    return duplicate;
}

Java Implementation

import java.util.*;

public class FindDuplicate{
    public static int findDuplicate(ArrayList<Integer> arr, int length){
        int duplicate = -1;
        // Create a frequency table count of size length.
        // count[i] = Frequency of i in arr.
        int[] count = new int[length];
        for (int i = 0; i < length; i++) {
            // For each element arr[i], increment count[arr[i]] by 1.
            int x = arr.get(i);
            count[x]++;
            if (count[x] > 1) {
                // If count[arr[i]] > 1, then we have found the duplicate element.
                duplicate = arr.get(i);
                break;
            }
        }
        return duplicate;
    }
}

Python3 Implementation

def findDuplicate(arr:list, length:int):
    duplicate = -1
    # Create a frequency table count of size length.
    # count[i] = Frequency of i in arr.
    count = [0] * length

    for i in range(0, length):
        # For each element arr[i], increment count[arr[i]] by 1.
        count[arr[i]] += 1
        if count[arr[i]] > 1:
            # If count[arr[i]] > 1, then we have found the duplicate element.
            duplicate = arr[i]
            break

    return duplicate

Time Complexity Analysis

In this method, we are doing a single iteration over array A and updating the count in the frequency table. Hence the complexity of this solution is $O (N)$ .

Time complexity: $O (N)$

Space Complexity Analysis

This method requires a frequency table for calculating the answer. The frequency table is implemented using an array of size N+1. So, the space complexity is O(N).

Space complexity: $O (N)$ .

Approach 7: Sum of Elements

This method is useful if it is known that there is only one duplicate element. If the problem specifies a new constraint, that there can be only one duplicate element, then we can use the following math trick to find that duplicate element efficiently.

We know that array $A$ contains $N$ elements from $1$ to $N$ and one duplicate element. Let us say that the duplicate element in the array is $D$ .

Now we can write,
(Sum of elements from $1$ to $N$ ) $+$ D = Sum of elements in array $A$
From this, we can derive
$D$ = Sum of elements in array $A$ $-$ Sum of elements from $1$ to $N$ .
We also know that the sum of elements from $1$ to $N$ is $N * (N + 1) / 2$ .

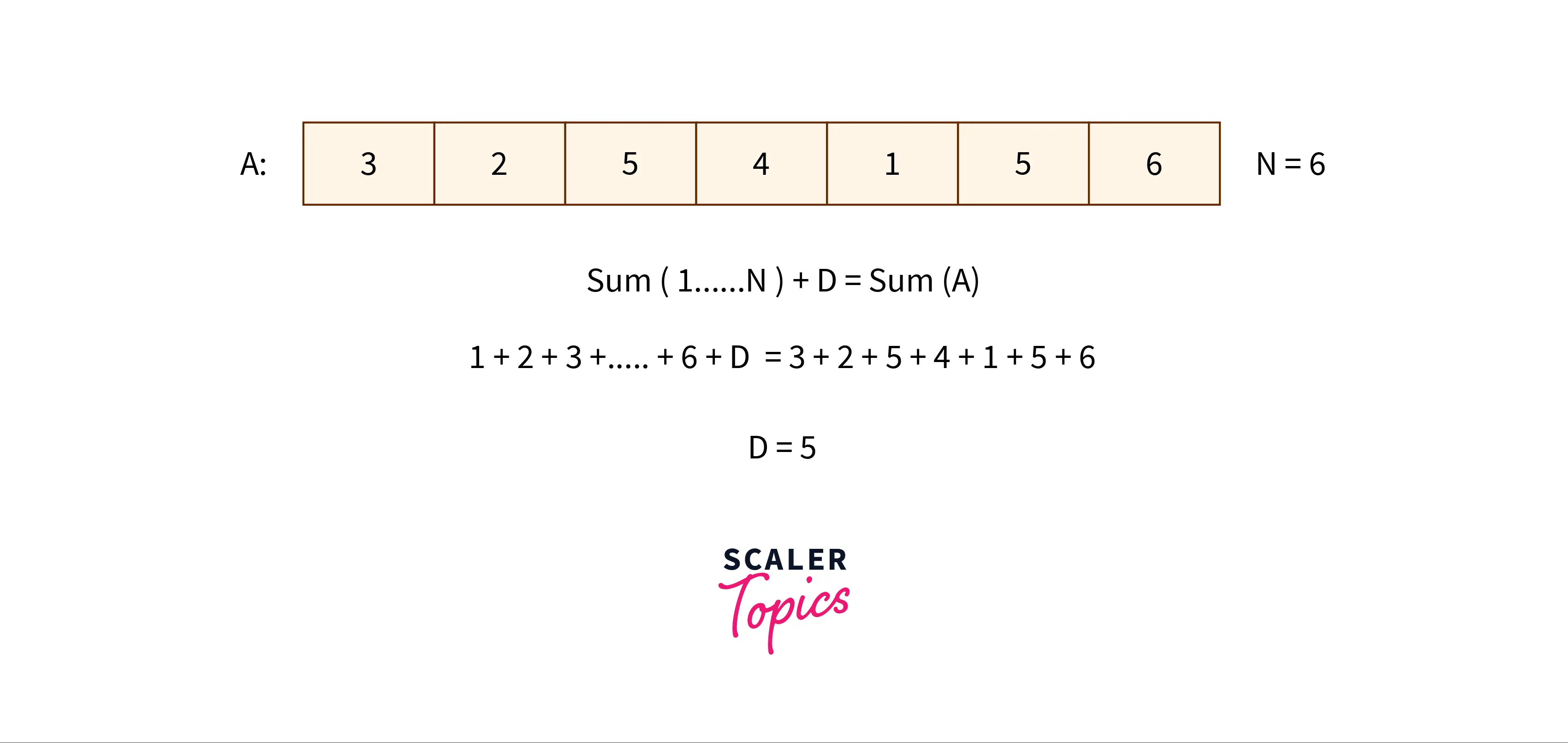
The only thing we need is the sum of elements in array $A$ , which can be calculated using a simple iteration over the array.
In this way, we can find the required duplicate element in array $A$ .
Note that, this method is only useful when it is given that there is only one duplicate element. If this is not the case, then this method will fail as the equation defined above does not holds good.

C++ Implementation

#include <bits/stdc++.h> 
using namespace std;

int findDuplicate(vector<int> &arr, int length){
    // Works only when there is exactly one duplicate element.
    int N = length - 1;
    int sum = accumulate(arr.begin(), arr.end(), 0);
    int duplicate = sum - ((N * (N + 1))/2);
    return duplicate;
}

Java Implementation

import java.util.*;

public class Solution{
    public static int findDuplicate(ArrayList<Integer> arr, int length){
        // Works only when there is exactly one duplicate element.
        int duplicate = -1, sum = 0, N = length - 1;
        for(int x : arr) sum += x;
        duplicate = sum - (N * (N + 1))/2;
        return duplicate;
    }
}

Python3 Implementation

def findDuplicate(arr:list, length:int):
    # This works only when there is exactly one duplicate element.
    N = length - 1
    sum_of_list = sum(arr)
    duplicate = sum_of_list - ((N * (N + 1))//2)
    return duplicate

Time Complexity Analysis

To find the duplicate in array $A$ , we need the sum of elements of array A. This is done using a simple interaction over the array $A$ in $O (N)$ . Once we know the sum, we can find the duplicate element in $O (1)$ time. Hence the time complexity is $O (N)$ .

Time Complexity: $O (N)$

Space Complexity Analysis

We do not need any extra space to find the answer. We only need a variable to calculate the sum.

Space complexity: $O (1)$

Approach 8: Marker

In this approach, we will make use of the information given to us, that each element $A [i]$ lies in between $1$ and $N$ .

Suppose we take a boolean $f l a g$ array of size N with all entries as $0$ . Now for each element $A [i]$ , we assign $f l a g [A [i]] = 1$ . Now as we are doing the iteration, if we arrive at an element A[i] such that $f l a g [A [i]]$ is already one, then, in this case, we can determine that the $A [i]$ is a duplicate.

This is because if the value of $f l a g [A [i]]$ is $1$ , this means that we have already encountered $A [i]$ before in the iteration. This $f l a g$ variable serves as a marker. When we are iterating over the elements of $A$ , we are marking each element $A [i]$ being visited using the array flag.

Space Optimization:
In this approach, we can optimize space as well. We are given positive elements in array $A$ , so we can use the same array as a flag array. Suppose, while iterating over A, to mark the element $A [i]$ , we make $A [A [i]]$ as negative. In this way, we can say that if at any time, we encounter an element x such that $A [x]$ is negative, then this will tell us that x is a duplicate element. During the iteration, we will consider the absolute values of $A [i]$ as the negative sign indicates that the index is marked by some previous element. This technique helps us to reuse memory and reduce space complexity.

Example
Consider array $A = [3, 2, 4, 1, 5, 2]$
Iteration 1: $A = [3, 2, 4, 1, 5, 2]$
Make $A [3]$ as negative. $A = [3, 2, 4, - 1, 5, 2]$

Iteration 2: $A = [3, 2, 4, - 1, 5, 2]$
Make $A [2]$ as negative. $A = [3, 2, - 4, - 1, 5, 2]$

Iteration 3: $A = [3, 2, - 4, - 1, 5, 2]$
Make $A [4]$ as negative. $A = [3, 2, - 4, - 1, - 5, 2]$

Iteration 4: $A = [3, 2, - 4, - 1, - 5, 2]$
Make $A [1]$ as negative. $A = [3, - 2, - 4, - 1, - 5, 2]$

Iteration 5: $A = [3, - 2, - 4, - 1, - 5, 2]$
Make $A [5]$ as negative. $A = [3, - 2, - 4, - 1, - 5, - 2]$

Iteration 6: $A = [3, - 2, - 4, - 1, - 5, - 2]$
Now, we see that $A [2]$ is already negative, so we know that the duplicate element is 2.

C++ Implementation

#include <bits/stdc++.h> 
using namespace std;

int findDuplicate(vector<int> &arr, int length){
    int duplicate = -1;
    for (int i = 0; i < length; i++) {
        int curr = arr[i];
        // For each element arr[i], check if arr[abs(arr[i])] > 0.
        if (arr[abs(curr)] > 0) {
            // In this case, we mark arr[abs(arr[i])] as negative.
            arr[abs(curr)] = -1 * arr[abs(curr)];
        } 
        else {
            /* In thie case, arr[i] was already visited, 
            so we have the duplicate element. */
            duplicate = abs(curr);
            break;
        }
    }
    return duplicate;
}

Java Implementation

import java.util.ArrayList;

public class Solution{
    public static int findDuplicate(ArrayList<Integer> arr, int length){
        int duplicate = -1;
        for (int i = 0; i < length; i++) {
            // For each element arr[i], check if arr[abs(arr[i])] > 0.
            int curr = arr.get(i);
            if (arr.get(Math.abs(curr)) > 0) {
                // In this case, we mark arr[abs(arr[i])] as negative.
                arr.set(Math.abs(curr), -1 * arr.get(Math.abs(curr)));
            } 
            else {
                /* In thie case, arr[i] was already visited, 
            so we have the duplicate element. */
                duplicate = Math.abs(curr);
                break;
            }
        }
        return duplicate;
    }
}

Python3 Implementation

def findDuplicate(arr:list, length:int):
    duplicate = -1;
    for i in range(length):
        # For each element arr[i], check if arr[abs(arr[i])] > 0.
        curr = arr[i];
        if arr[abs(curr)] > 0:
            # In this case, we mark arr[abs(arr[i])] as negative.
            arr[abs(curr)] = -1 * arr[abs(curr)]
        else:
            # In thie case, arr[i] was already visited, 
            # so we have the duplicate element.
            duplicate = abs(curr)
            break
    return duplicate;

Time Complexity Analysis

In this method, we are iterating over the array A once, hence the time complexity is $O (N)$ .

Time complexity: $O (N)$

Space Complexity Analysis

If you use a secondary array flag for marking each element, then the space complexity will be $O (N)$ .
If you re-use the same input array for marking each element, then the space complexity of our algorithm is $O (1)$ .

Conclusion

There are many methods, discussed in this article, to find duplicates in an array.
Some techniques like Binary search over an array or method using the sum of elements are only applicable only if there is a single duplicate element.
Other techniques like using a frequency table or hash tables can be applied to a more general problem.
The linked list cycle technique can be applied only when elements range from 1 to N.
From this problem, you can learn how to apply different types of techniques to the same problem. It is essential to understand each algorithm and the complexity analysis.

Author

Prajwal Agarwal

View all posts

Find Duplicates in Array

Problem Statement

Example 1

Example 2

Constraints

Problem Discussion

Approach 1: Brute Force

C++ Implementation

Java Implementation

Python3 Implementation

Time Complexity Analysis

Space Complexity Analysis

Approach 2: Using Sorting

C++ Implementation

Java Implementation

Python3 Implementation

Time Complexity Analysis

Space Complexity Analysis

Approach 3: Using Frequency Array

C++ Implementation

Java Implementation

Python3 Implementation

Time Complexity Analysis

Space Complexity Analysis

Approach 4: Linked List Cycle Method

C++ Implementation

Java Implementation

Python3 Implementation

Time Complexity Analysis

Space Complexity Analysis

Approach 5: Binary Search on Array

C++ Implementation

Java Implementation

Python3 Implementation

Time Complexity Analysis

Space Complexity Analysis

Approach 6: Count Iterations

C++ Implementation

Java Implementation

Python3 Implementation

Time Complexity Analysis

Space Complexity Analysis

Approach 7: Sum of Elements

C++ Implementation

Java Implementation

Python3 Implementation

Time Complexity Analysis

Space Complexity Analysis

Approach 8: Marker

C++ Implementation

Java Implementation

Python3 Implementation

Time Complexity Analysis

Space Complexity Analysis

Conclusion

Author

Latest articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Featured articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?