Java Program to Display Floyd’s Triangle

What is Floyd’s Triangle?

Floyd's Triangle is an intriguing numerical pattern that appears regularly in programming, notably in Java. This triangle, named after American computer scientist Robert W. Floyd, is a right-angled triangular array of natural integers. The pattern begins with the number 1 at the top and proceeds in ascending order, generating rows with an increasing number of pieces.

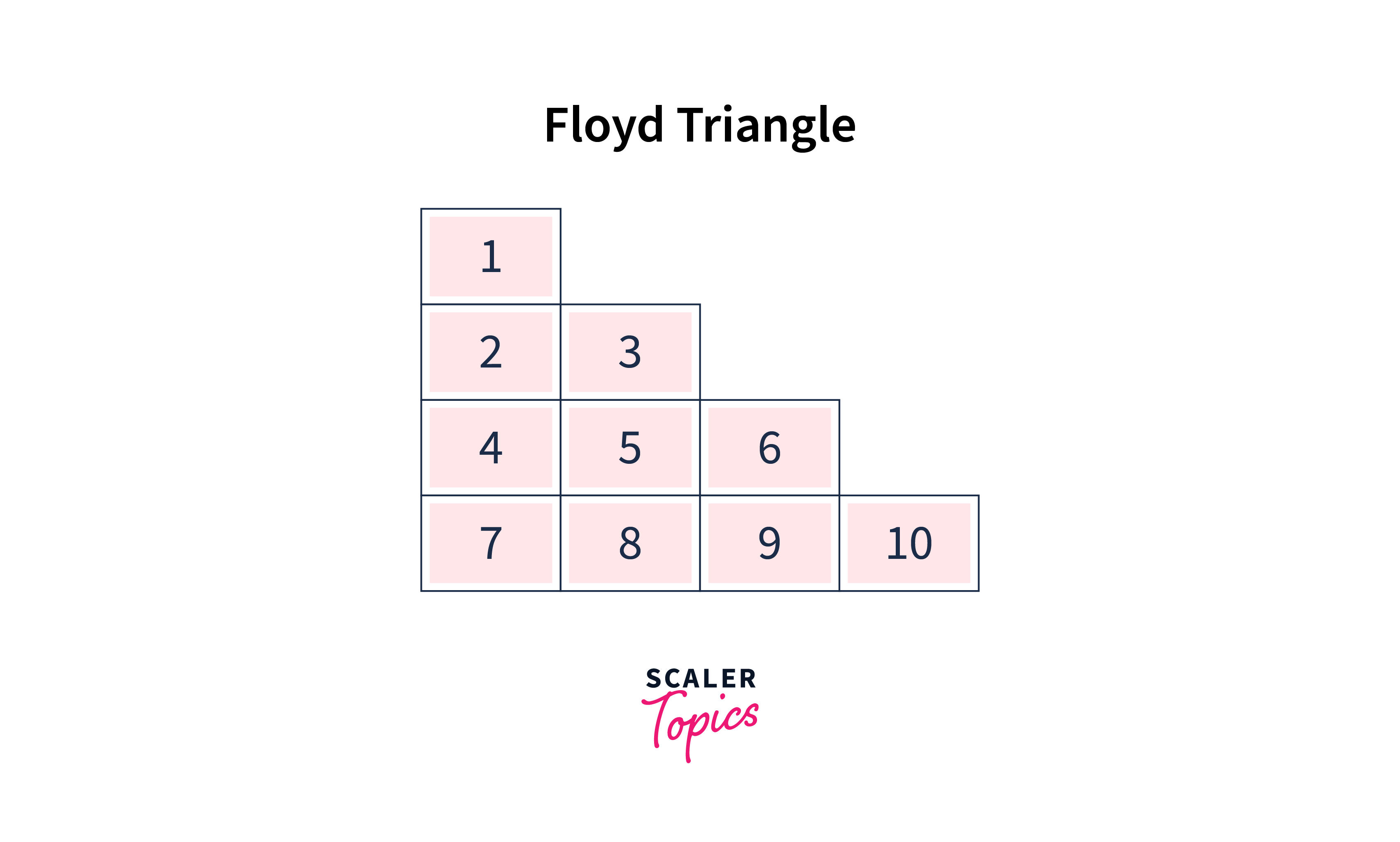
Creating Floyd's Triangle in Java is a simple effort. Nested loops can regulate the row and column count, with a variable tracking and printing the numbers progressively. This pattern is frequently used to teach loop structures, particularly nested loops since it displays a basic yet beautiful method of systematically organizing and displaying data.

A Java code snippet to print Floyd's Triangle up to a specific number n, for example, would include two nested loops, one for rows and one for columns. As the numbers increase, they form a unique triangular arrangement, making it a useful instructional tool and a fun programming challenge.

Java Program to Display Floyd’s Triangle

Floyd's Triangle is a simple yet fascinating numerical pattern named after prominent American computer scientist Robert W. Floyd. This triangle is made by filling a right-angled triangular form with rows of successive natural integers beginning with 1. It's a great exercise for beginners to learn the fundamentals of loops and conditional expressions in Java.

Illustration

Before diving into the Java code, let's understand how Floyd's Triangle looks. For a given number of rows n, the triangle begins with 1 in the first row, followed by 2, 3, and so on, until n numbers are reached in the nth row. Here's an illustration for n = 5:

Algorithm

The algorithm for creating Floyd's Triangle is simple:

• Initialize two variables, row and num, both set to 1.
• Take user input for the number of rows n for Floyd's Triangle.
• Start the outer loop to iterate through the rows. The outer loop runs from row = 1 to row = n.
• Inside the outer loop, start the inner loop to control the columns. The inner loop runs from col = 1 to col = row.
• Inside the inner loop:
  • Print the value of num. This is the current integer that will be part of the Floyd's Triangle.
  • Increment num by one to prepare for the next integer.
• After printing all the numbers in the current row, insert a newline character (\n) to move to the next row. This newline character ensures that the triangle is properly formatted, with each row on a new line.
• Repeat steps 4 to 6 for each row until the outer loop (row) reaches the required number of rows n.
• The program ends, and you have successfully created and displayed Floyd's Triangle based on the user's input.

The key to understanding this algorithm is the use of nested loops. The outer loop controls the rows, and the inner loop controls the columns within each row. As the inner loop progresses, it prints the sequential numbers (num) and increments them for the next iteration, creating the successive integer pattern that forms Floyd's Triangle. The newline character ensures that each row starts on a new line, maintaining the triangle's shape.

Implementation

Now, let's implement the algorithm in Java:

Explanation

In this Java program, we:

• Take the user's input for the number of rows (n).
• We use nested loops to go through the rows and columns, outputting the num at each point.
• After printing each number, the variable num is increased.
• A newline character is written after each row to format the triangle properly.

Construct and execute this program, displaying Floyd's Triangle with the rows chosen. It's a wonderful way to practice loops and output formatting in Java.

Example

Let's walk through an example of running the Java program to display Floyd's Triangle with four rows.

In this example:

• The user is invited to enter the number of rows, which we enter as "4".
• The program then produces Floyd's Triangle with four rows, as illustrated above.
• Each row has consecutive natural integers beginning with one and increasing by 1 in each position.
• The digits are printed in a right-angled triangle design called Floyd's Triangle.

Complexity Analysis

Let's analyze the time and space complexity of the Java program that displays Floyd's Triangle with n rows:

Time Complexity Analysis:

The time complexity of this program primarily depends on the nested loops used to print the numbers in Floyd's Triangle.

• The outer loop is executed n times, where n is the user-specified number of rows. This loop controls the number of rows in the triangle.
• The inner loop executes incrementally depending on the current row number. In the worst-case scenario, the inner loop will execute 'n' times for the last row, but this number steadily lowers as we advance along the rows.

To compute the total number of inner loop iterations across all rows, add the integers from 1 to n. The arithmetic series sum formula calculates this sum $(n * (n + 1)) / 2$.

So, the overall time complexity of the program can be approximated as $O(n^2)$, where n is the number of rows. This means the program's execution time increases quadratically with the increased number of rows.

Space Complexity Analysis:

The amount of memory utilized to store variables and data structures determines the program's space complexity. The memory utilization in this program is pretty low:

The integer variables n, num, row, and col consume constant space, regardless of the value of n. Therefore, their space complexity is $O(1)$.

The Scanner object input and the dynamically allocated memory for the strings "Enter the number of rows for Floyd's Triangle: " and "Floyd's Triangle:" also consume constant space, so their space complexity is $O(1)$.