GCD of Two Numbers in Java

The Greatest Common Divisor (GCD), or Highest Common Factor (HCF), is the largest number that divides two numbers without a remainder. It can be calculated using methods like the naive loop approach, the Euclidean algorithm by subtraction, and the Euclidean algorithm with modulo operation. The Greatest Common Divisor (GCD) reflects common factors in prime factorizations.

Algorithm to Find GCD

The algorithm to find the GCD of two numbers that comes intuitively to most people is to check the divisibility of both the numbers in a loop from numbers 1 to $min(a,b)$, then return the biggest number that divides both of them, thus, GCD of two numbers.

How to Find the Greatest Common Factor?

In Java, we can find the GCD (Greatest Common Factor) of two numbers using the ways discussed below:

Find GCD of Two Numbers Using for Loop and if Statement

We can find the GCD of two numbers in Java using a for loop and an if condition from checking the greatest integer dividing both the numbers by iterating from 1 to $min(a,b)$.

Steps of the Algorithm:

1. Take two numbers (a and b) as input from the user to find their GCD.
2. Initialize a variable to store the GCD with an initial value of $1$.
3. Check if a or b is equal to 0, if yes, store the non-zero number in the GCD variable. If this condition satisifies, step 4 will be skipped.
4. Iterate from 1 to $min(a,b)$ and check if the number divides both a and b, if yes, then store it in GCD.
5. Print the GCD.

Example:

Source Code

Output:

Explanation:

In the above example, we are finding the GCD of two numbers (a and b) by iterating from 1 to $min(a,b)$ and checking the divisibility of the numbers, the greatest number that divides both a and b is the GCD of a and b.

Complexity Analysis:

• Time Complexity: $O(min(a, b))$ In this algorithm, we are iterating from 1 to min(a,b) in a for loop, so the time complexity will be O(min(a,b)).

• Space Complexity: $O(1)$ The space complexity here is constant as we are using constant space.

Find GCD of Two Numbers Using While Loop and if Statement

We can use a while loop and an if condition to find out the GCD of two numbers in Java using the above algorithm. Steps of the Algorithm:

1. Take two numbers (a and b) as input from the user to find their GCD.
2. Initialize a variable to store the GCD with an initial value of $1$.
3. Check if a or b is equal to 0, if yes, store the non-zero number in the GCD variable. If this condition satisifies, step 6 will be skipped.
4. Initialize a variable i = 1 for the while loop.
5. Run a while loop unless the following condition is false: $i\leq min(a,b)$.
6. In each iteration, check if the number divides both $a$ and b, if yes, then store it in GCD. Increment i.
7. After the end of while loop, print the GCD.

Examples:

Source Code

Output:

Explanation:

In the above example, we are finding the GCD of two numbers (a and b) using a while loop iterating as long as $i\leq min(a,b)$, we are checking if a and b are divisible by i or not in each iteration, if yes, then we will store the value of $i$ in GCD. The final value of the GCD after the end of the while loop will be our result.

Complexity Analysis:

• Time Complexity: $O(min(a, b))$ In this algorithm, we are iterating from 1 to min(a,b) in a for loop, so the time complexity will be O(min(a,b)).

• Space Complexity: $O(1)$ The space complexity here is constant.

Find GCD of Both Positive and Negative Numbers

The GCD is always positive irrespective of the sign of the input numbers. If the given number is negative, we will simply ignore its "-" sign using the abs() function. After making the negative numbers positive, we can find the GCD of two numbers (positive or negative) number using the for loop and an if condition algorithm by checking the divisibility of both the numbers (a and b) iterating from 1 to $min(a,b)$.

Steps of the Algorithm:

1. Take two numbers (a and b) as input from the user to find their GCD.
2. Initialize a variable to store the GCD with an initial value of $1$.
3. Assign $a=abs(a)$ $b=abs(b)$.
4. Check if a or b is equal to 0, if yes, store the non-zero number in the GCD variable. If this condition satisifies, step 5 will be skipped.
5. Iterate from 1 to min(a,b) and check if the number divides both a and b, if yes, then store it in GCD.
6. Print the GCD.

Example:

Source Code

Output:

Explanation:

In the above example, we are finding the GCD of two numbers (a and b) which maybe positive or negative by first assigning them their absolute values (using the Math abs() function) and then iterating from 1 to min(a,b) and checking the divisibility of the numbers, the greatest number that divides both a and b is the GCD of a and b.

Complexity Analysis:

• Time Complexity: $O(min(a,b))$ In this algorithm, we are iterating from 1 to $min(a,b)$ in a for loop, so the time complexity will be O(min(a,b)).
• Space Complexity: $O(1)$ The space complexity here is constant.

Find GCD of Two Numbers Using User-Defined Method

Using a user-defined method to find the GCD of two numbers is a smarter way than writing the whole implementation in the main(), as we can use the method as a utility method to use it as many times as we want just by calling it, enhancing readability and maintenance of the program. We will be using the for loop and if condition method (discussed above) in the user-defined function.

Steps of the Algorithm:

1. Create a user-defined method called GCD() that accepts two integer parameters (a and b).
2. Inside the function, initialize a variable to store the GCD with an initial value of $1$.
3. Assign $a=abs(a)$ and $b=abs(b)$.
4. Check if b or a is equal to $0$, if yes, store the non-zero number in the GCD variable. If this condition satisifies, step 5 will be skipped.
5. Iterate from 1 to min(a, b) and check if the number divides both a and b, if yes, then store it in GCD.
6. Return GCD from the GCD() function.
7. Print the GCD in the main() function.

Example:

Source Code

Output:

Explanation:

In the above example, we are finding the GCD of two numbers (a and b) by calling a user-defined method called GCD() which assigns the numbers their absolute values and iterates from $1$ to min(a,b) to check if $i$ divides $a$ and $b$, if yes, GCD variable will store i, after the end of the while loop, the GCD variable will be equal to the greatest common divisor of a and b.

Complexity Analysis:

• Time Complexity: $O(min(a, b))$ In this algorithm, we are iterating from 1 to $min(a,b)$ in a for loop, so the time complexity will be O(min(a,b)).

• Space Complexity: $O(1)$ The space complexity here is constant.

Find GCD of Two Numbers Using Euclidean Algorithm by Subtraction

To find the GCD of two numbers using recursion, we will be using the principle $GCD(a,b)=GCD(a,b-a)$, its proof is discussed in the section "Find GCD of two numbers Using the Euclidean Algorithm" above.

Steps of the Algorithm

1. Check if $a==0$, if yes, return b.
2. Check if $b==0$, if yes, return a.
3. Check if $a==b$, if yes, return a.
4. Check if $a>b$ if yes, call GCD() function using the arguments $a-b$ and $b$ recursively, otherwise call GCD() function using the arguments $a$ and $b-a$

Example:

Source Code

Output:

Explanation:

In the above example, we are finding the GCD of two numbers (a and b) using recursion following the principle that $GCD(a,\;b) = GCD(a - b, \; b)$ assuming $a > b$. If the base cases are not followed we will recursively call the GCD() function. GCD(a, b - a) if $b>a$ else GCD(a - b, b).

Complexity Analysis:

• Time Complexity: $O(max(a, b))$ In this algorithm, the number of steps are linear, for e.g. $GCD(x, 1)$, in which we will subtract $1$ from $x$ in each recursion, so the time complexity will be $O(max(a, b))$.

• Space Complexity: $O (max(a,b))$ The space complexity here is $O(max(a,b))$ because the space complexity in a recursive function is equal to the maximum depth of the call stack.

Find GCD of Two Numbers Using the Euclidean Algorithm

The Euclidean algorithm is an efficient way to calculate the GCD of two numbers. It is named after the ancient Greek mathematician Euclid who first described this algorithm in his books called Elements in 300 BC. This algorithm is based on the fact that $GCD(a,b)$ is equal to $GCD(a-b,b)$ as subtracting a smaller number from a larger number doesn't change their GCD. So if we keep subtracting the larger of the two, we will end up with their GCD.
The Eulidean Algorithm states that if $a=b*q+r$ and $b\neq 0$, where $q$ is the quotient and $r$ is the remainder, then $GCD(a,b) = GCD(b,r)$.
As discussed above, we already know that $GCD(a,b)=GCD(b,a-b)$, we can repeatedly apply this rule to itself to obtain, $GCD(a,b) = GCD(b,a-2*b) = GCD(b,a-3*b)=GCD(b,a-q*b)$. As $a-q*b=r$, it is proved that $GCD(a,b) = GCD(b,r)$.

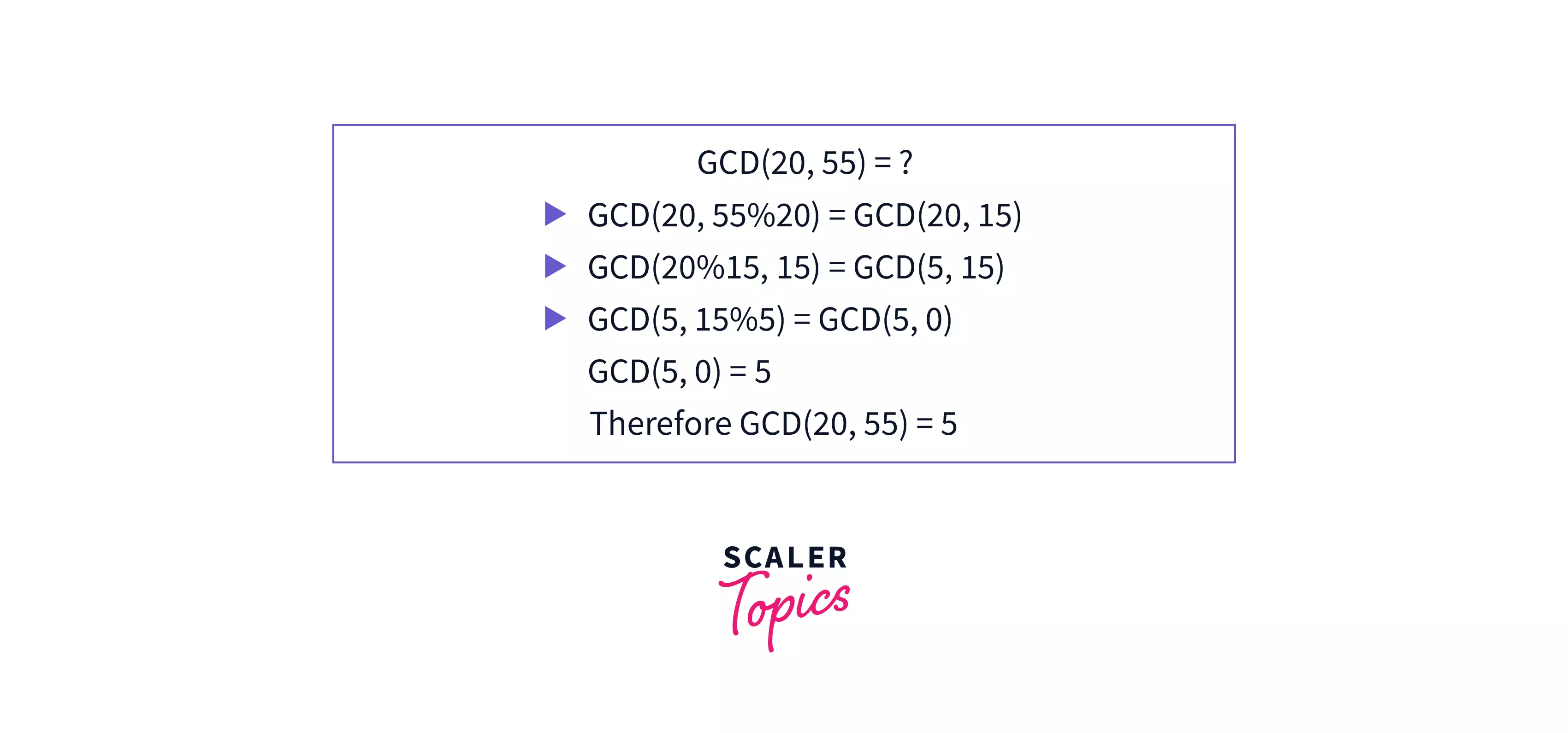
Steps of the Algorithm

1. Take two numbers (a and b) as input from the user to find their GCD.
2. Store the greater number among $a$ and $b$ in $x$, and the other one in y.
3. Initialize a variable r used to store the GCD of a and b.
4. Iterate in a while loop while $x\%y\not=0$
5. In each iteration, assign $r=x\%y$, $x=y$, and $y=r$.
6. After the end of the while loop, return the value r, that is the GCD of a and b.

Example:

Source Code

Output:

Explanation:

In the above example, we are finding the GCD of two numbers (a and b) using the Euclidean algorithm which states that $GCD(a,b) = GCD(b,a\%b)$ where a > b. In this algorithm, we are using a while loop in which we are assigning $r=x\%y$, $x=y$, and $y=r$ till $x\%y != 0$. The value of r after the end of the loop will be equal to the GCD of a and b.

Complexity Analysis:

• Time Complexity: $O(log\;min(x,y))$ In this algorithm, we are iterating in the while loop till $x\%y=0$ We are reducing $y$ to $x\%y$ in each iteration, so the time complexity will be $O(log\;min(x,y))$.For in-depth analysis of time complexity of Euclidean Algorithm, follow Euclidean Algorithm article from Scaler Topics.

• Space Complexity: $O(1)$ The space complexity here is constant.

Find GCD of Two Numbers Using Recursion

We can find the GCD of two numbers using a modulo operator by the help of Euclidean Algorithm, which states that $GCD(a,b) = GCD(b,r)$, where r is the remainder after dividing a by b. The proof of the Euclidean Algorithm has been discussed in the above section

Steps of the Algorithm

1. In the user-defined method GCD(), check if $b==0$, if yes, return $a$.
2. If $b\not=0$, recursively call the GCD() function by passing the parameters $b$ and $a\%b$, i.e $GCD(b,a\%b)$.

Example:

Source Code

Output:

In the above example, we are implementing the Euclidean algorithm using recursion to find the GCD of two numbers. The base case here is: if $b==0$, then return $a$, otherwise, recursively call $GCD(b,a\%b)$.

Complexity Analysis:

• Time Complexity: $O(log \; min(a, b))$ In this algorithm, we are recursively calling $GCD(b,a\%b)$ reducing the second parameter by $a\%b$ in each function call, so the maximum number of steps required to reduce b to 0 will be: $O(log\;min(a,b))$.

• Space Complexity: $O(log \; min(a, b))$ In recursion, the space complexity is equal to the maximum depth of the call stack, i.e $O(log\;min(a,b))$.