Geometric Progression

Geometric Progression (GP) is a sequence where each term results from multiplying the previous one by a constant, known as the Common Ratio. Consider folding a paper multiple times: while it's folded 4-5 times, determining its final stack height illustrates GP principles. This progression concept offers insights into patterns formed by consistent multiplicative growth.

Notation

Lets deep dive into geometric progression and understand the various terminologies used in it.

1. First Term: Each number of the series is called a "term". Hence, the number from which the series starts is called the First Term. It is generally denoted by $a$. In our previous example, the first term is $1$.
2. Common ratio: The non-zero constant from which we were multiplying each of the terms is called the common ratio. It is generally denoted by $r$. In our previous example, this ratio is $2$.

General Form

Lets see the sequence again,

$\color{blue} 1,\ 2,\ 4,\ 8,\ 16,\ 32,\ 64\ ...$ $\implies \color{blue}1,\ \color{blue}1\times 2, \color{blue}1 \times (2\times 2),\ 1\times (2\times 2\times 2),\ 1\times (2\times 2\times 2\times 2),\ \color{blue}1\times (2\times 2\times 2\times 2\times 2),\ \color{blue}1\times (2\times 2\times 2\times 2\times 2\times 2),\ ...$ $\implies \color{blue}1,\ \color{blue}1\times 2^1,\ \color{blue}1\times 2^2,\ \color{blue}1\times 2^3,\ \color{blue}1\times 2^4, \ \color{blue}1\times 2^5,\ \color{blue}1\times 2^6\ ...$

Let $\color{blue}{a=1}$ and $r=2$,

$\implies \color{blue}a,\ \color{blue}a \times r^1,\ \color{blue}a\times r^2,\ \color{blue}a\times r^3,\ \color{blue}a\times r^4, \ \color{blue}a\times r^5,\ \color{blue}a\times r^6\ ...$

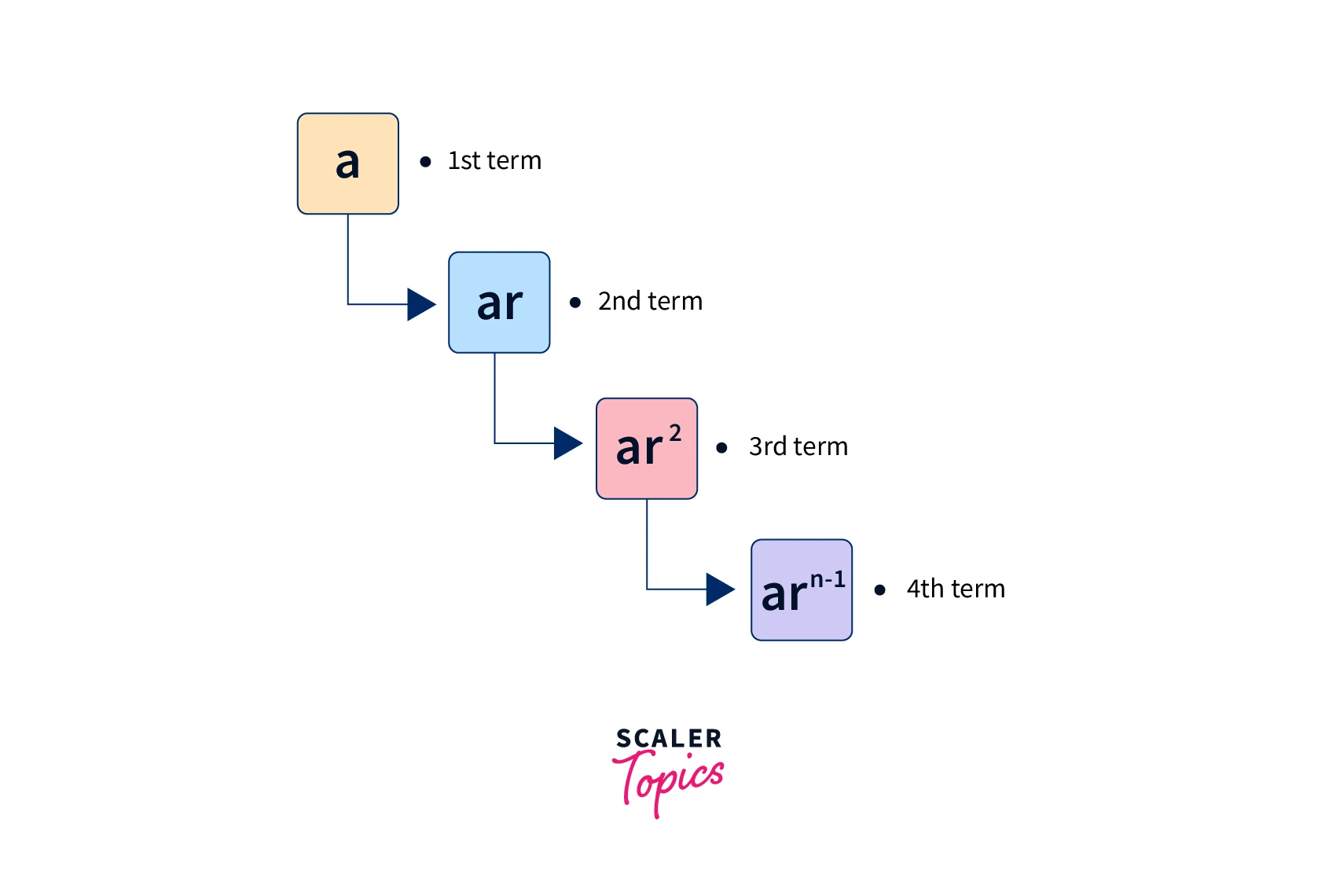
Hence we say, in general, geometric progression is of the form $a, ar, ar^2, ar^3, ar^4,…, ar^{n-1}$

where,

$a =$ First term

$r =$ common ratio

$ar^{n-1} =$ nth term

Nth Term

Intuition

When we write the formula for the nth term of the GP series, we try to generalize the last term of a finite GP in terms of the first term and the common ratio of the GP.

Derivation

Let $a$ be the first term and $r$ be the common ratio for a Geometric Sequence.

Then, the second term, $a_2 = a \times r = ar$

Third term, $a_3 = a_2 \times r = ar \times r = ar^2$

Similarly, nth term, $a_n = ar^{n-1}$

Formula

The formula to find the nth term of GP is:

$a_n = ar^{n-1}$

We use "n-1" because $ar_0$ is for the 1st term and $r_0$ is 1.

Example

Consider the following sequence,

$1, 2, 4, 8, 16, 32, 64\ ...$

Here, $a_1 = 1\times 2^0 =1$ $a_2 = 1\times 2^1 =2$ $a_3 = 1\times 2^2 =4$ $a_3 = 1\times 2^3 =8$ $a_4 = 1\times 2^4 =16$ $a_5 = 1\times 2^5 =32$ $a_6 = 1\times 2^6 =64$ and so on.

Types of GP

A geometric progression can be finite or infinite depending on the number of terms it contains. Let's see a brief description about both of them.

Finite GP

• If the number of terms in a geometric progression is finite then it is called a finite GP.
• In general, we can write finite GP as $a, ar, ar^2, ar^3,...,ar^{n-1}$.
• For example, $1, 2, 4, 8, 16, 32, 64$ is a finite GP.

Infinite GP

• If the number of terms in a geometric progression is infinite then it is called an infinite GP.
• In general, we can write infinite GP as $a, ar, ar^2,...,ar^{n-1},...$.
• For example, $1, 2, 4, 8, 16, 32, 64,\ ...$ is an infinite GP.

Sum of GP for Nth term

Intuition

As we have seen earlier, in a GP sequence every term can be expressed with the help of the first term($a$) and the common ratio($r$). Similarly we can express the sum of geometric progression in terms of $a$ and $r$.

Derivation

Let's see how we can derive the formula for finite GP.

First, call the whole sum $S$:

$S = a + ar + ar^2 + ... + ar^{n-2}+ ar^{n-1}$

Next, multiply $S$ by $r$:

$-S. r = ar + ar^2 + ... + ar^{n-1} + ar^n$

Notice that $S$ and $S·r$ are similar?

Now subtract them!

$S = a + ar + ar^2 + ... + ar^{n-2}+ ar^{n-1}$

$-S·r = ar + ar^2 + ar^3 + ... + ar^{n-1} + ar^n$

$\implies S - S·r = a - ar^n$ $\implies S(1-r) = a(1 - r^n)$ $\implies S = a\frac{(1 - r^n)}{(1-r)}$

Formula

The formula for the sum of $n$ terms of a finite GP is given as:

$S = \sum_{k=0}^{n-1}(ar^k) = a\frac{(1 - r^n)}{(1-r)}$

When GP is infinite, i.e., $n \rightarrow \infty$

$S = \sum_{k=0}^{\infty}(ar^k) = a\frac{1 }{(1-r)}$