Geometric Transformation in Computer Vision

Computer vision and geometric transformations are essential components in various applications such as object detection, image segmentation, and augmented reality. Geometric transformations play a crucial role in aligning and transforming images for improved analysis and feature extraction. Several traditional algorithms, as well as machine learning-based approaches, have been developed for geometric transformations in computer vision. Despite the challenges, the potential future directions for geometric transformations in computer vision include self-supervised learning, deep reinforcement learning, and real-time implementation on embedded devices.

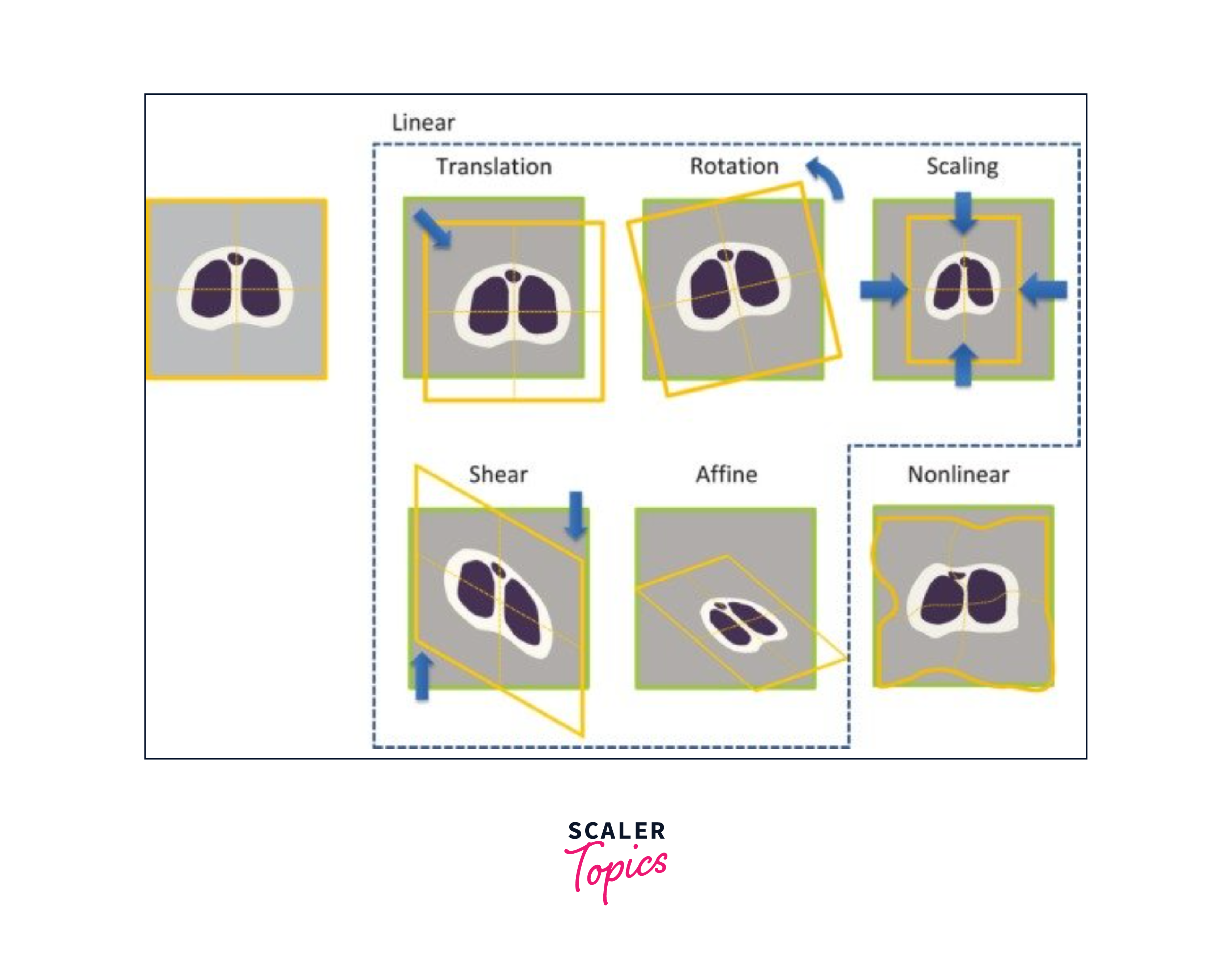
Types of Geometric Transformations

The four main types of geometric transformations used in computer vision are translation, rotation, scaling, and shearing. These transformations enable systems to recognize objects regardless of their orientation, stabilize videos, and create visual effects in computer graphics.

1. Translation:

Translation is a geometric transformation that involves moving an object or image in a certain direction without changing its size or shape. In image processing, translation is commonly used to align images, correct motion blur, and create panoramic images. The translation operation can be represented mathematically as a 2D or 3D vector that specifies the distance and direction of the movement.

2. Rotation:

Rotation is a geometric transformation that involves rotating an object or image around a certain point or axis. In computer vision, rotation is commonly used to align images, detect and recognize objects regardless of their orientation, and create visual effects in computer graphics. The rotation operation can be represented mathematically using a rotation matrix that specifies the angle and axis of rotation.

3. Scaling:

Scaling is a geometric transformation that involves changing the size of an object or image by either enlarging or reducing its dimensions. Scaling can be performed independently on each dimension of an object or image. In computer vision, scaling is commonly used to resize images, normalize image sizes, and generate image pyramids. The scaling operation can be represented mathematically using a scaling matrix that specifies the scaling factors in each dimension.

4. Shearing:

Shearing is a geometric transformation that involves skewing an object or image along one of its axes. In computer vision, shearing is commonly used to correct image distortions, perform perspective transformations, and create visual effects in computer graphics. The shearing operation can be represented mathematically using a shearing matrix that specifies the shear factors in each dimension.

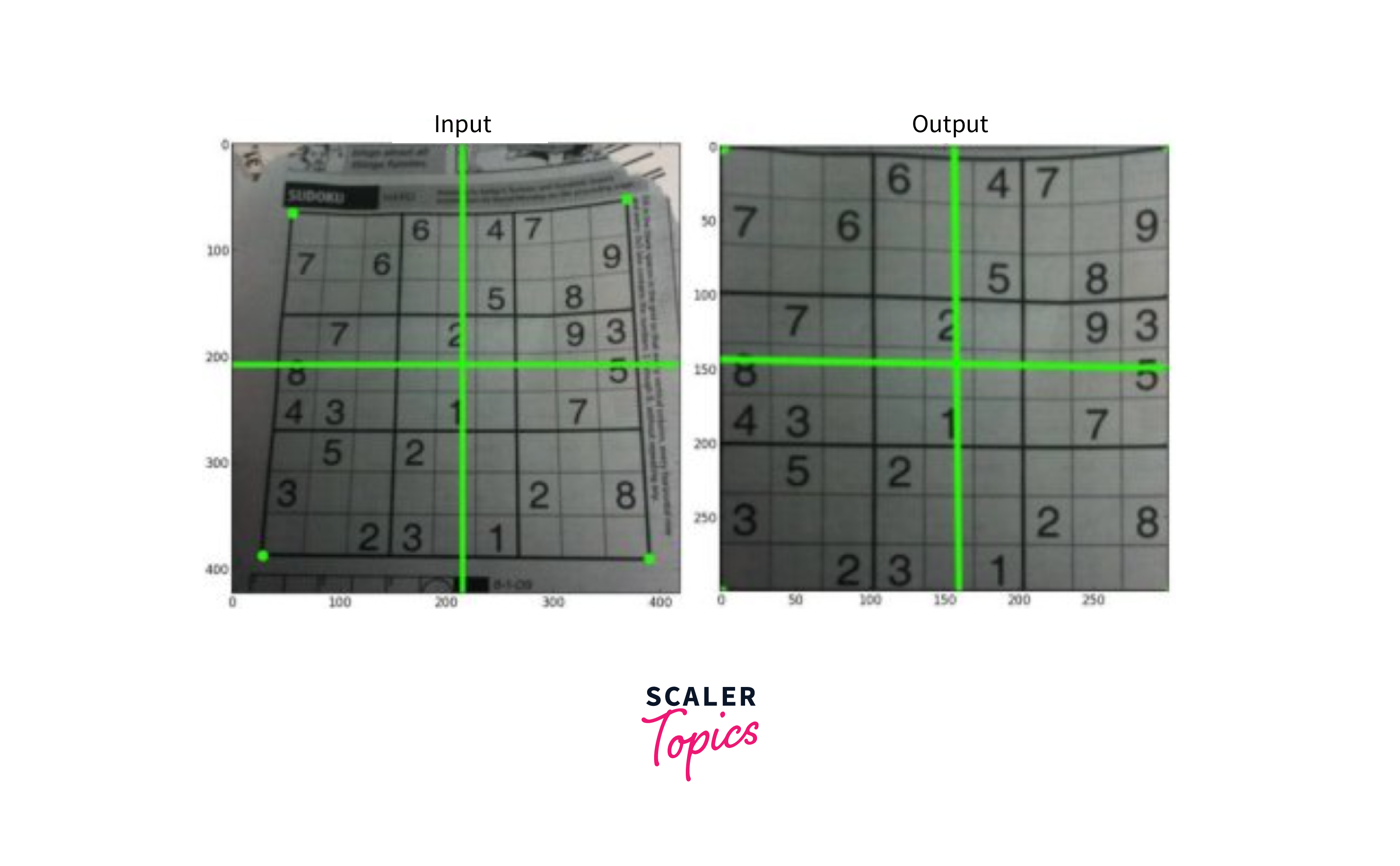
Perspective Transformation

Perspective transformation is a geometric transformation that involves skewing an image to make it appear as though it is viewed from a different angle. This transformation is used in computer vision applications such as image stitching, where multiple images are merged into a single panoramic image. To perform a perspective transformation, you need a 3x3 transformation matrix that can be found using 4 points on the input image and corresponding points on the output image.

The process of finding the transformation matrix involves selecting four points on the input image and their corresponding points on the output image. It is important to note that among these four points, three of them should not be collinear (i.e., they should not lie on a straight line). The four points are used to find the transformation matrix using the function cv2.getPerspectiveTransform.

Once the transformation matrix is found, it can be applied to the input image using the function cv2.warpPerspective. This function takes the input image and the 3x3 transformation matrix as input parameters and applies the perspective transformation to the input image. After the transformation is applied, straight lines in the input image will remain straight in the transformed image.

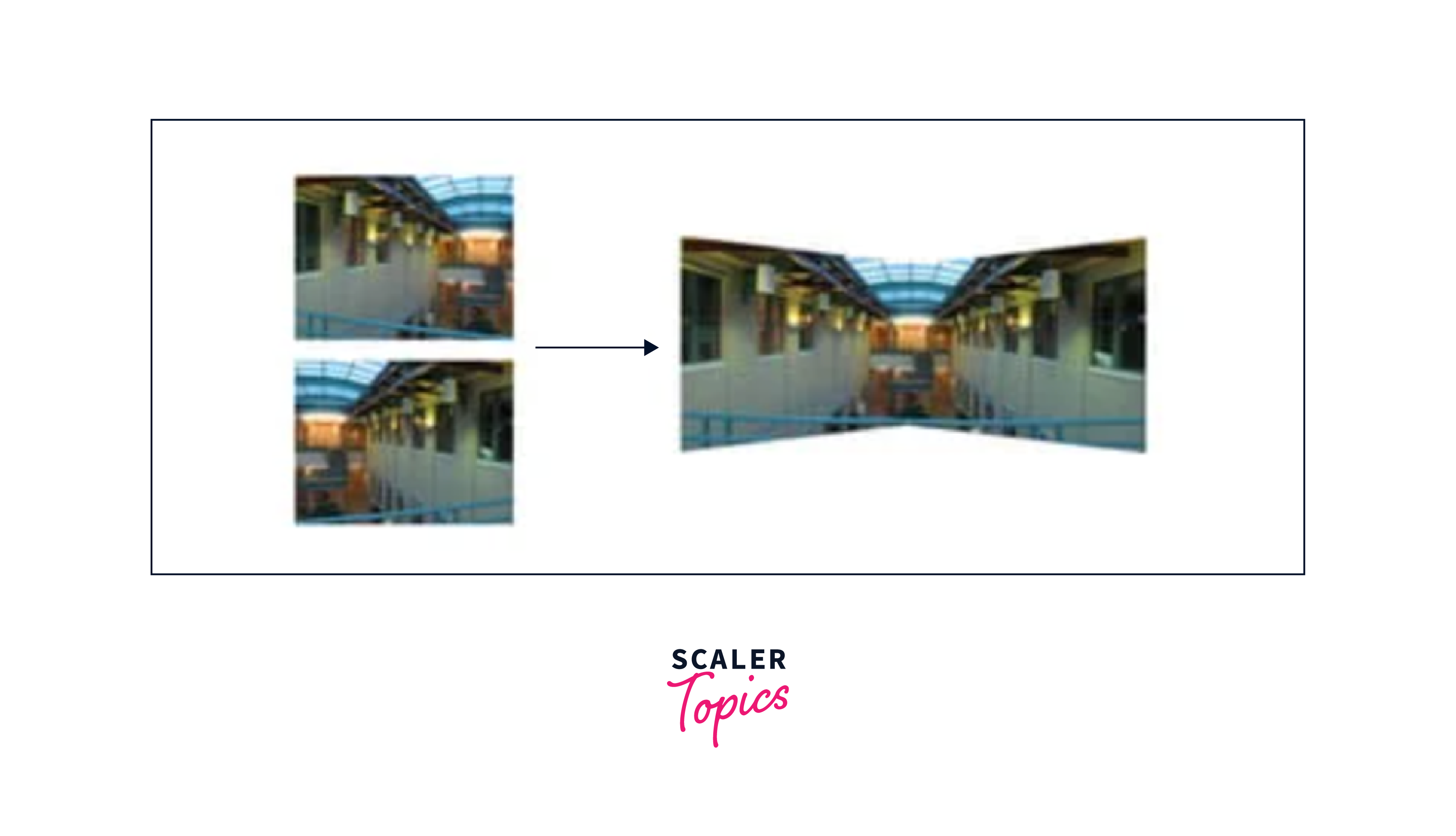
Geometric Transformation Techniques in Computer Vision

Geometric Transformation techniques are fundamental tools in computer vision that enable a wide range of applications. By applying these techniques, computer vision systems can correct distortions, remove noise, enhance the quality of images and videos, and recognize objects regardless of their position or orientation.

Homography Estimation

• Homography estimation is the process of estimating the transformation between two images.
• It is commonly used in image stitching, where multiple images are merged into a single panoramic image.
• Homography estimation involves finding a 3x3 transformation matrix that maps one image to the other.
• This can be done by selecting corresponding points in both images and solving a system of linear equations.

Feature Matching

• Feature matching is a technique used to match features between two images in order to estimate the transformation between them.
• This technique involves detecting features in both images, such as corners or edges, and then matching the corresponding features.
• Feature matching is commonly used in applications such as object recognition, where the goal is to recognize an object in different images regardless of its position or orientation.

RANSAC

• RANSAC (Random Sample Consensus) is a robust algorithm used for estimating the transformation between two images.
• RANSAC is particularly useful when there are outliers in the feature matching process, which can result in incorrect estimates.
• RANSAC works by randomly selecting a subset of the features and estimating the transformation based on those features.
• This process is repeated multiple times, and the best estimate is chosen as the final result.

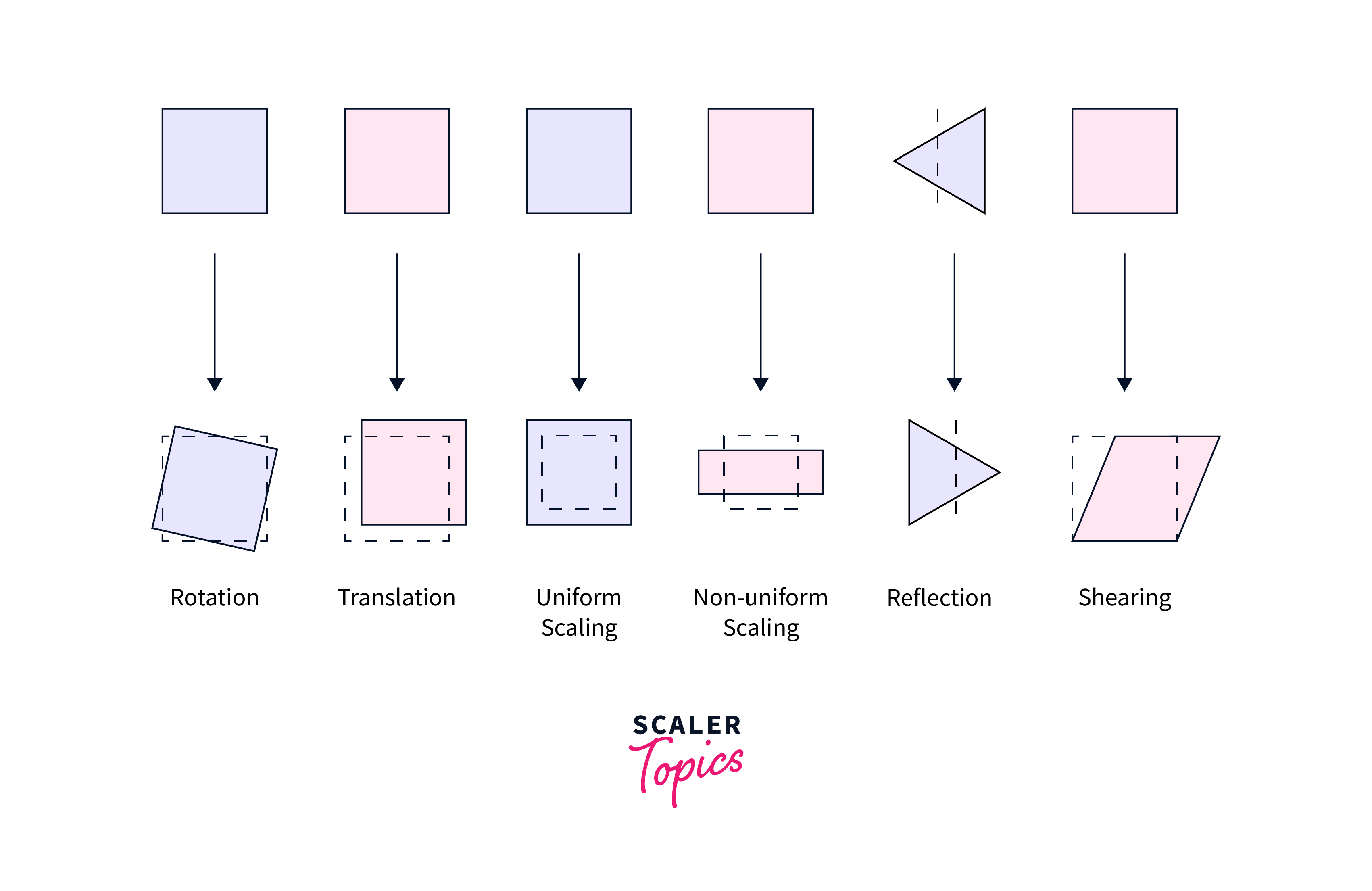
Affine Transform

• Affine transform is a geometric transformation that preserves straight lines, angles, and parallelism.
• It is a more general transformation than homography, which includes translation, rotation, scaling, and shearing.
• Affine transform can be used in applications such as image registration, where the goal is to align multiple images.
• In affine transform, the transformation matrix is a 2x3 matrix that includes the translation, rotation, and scaling parameters.

Applications of Geometric Transformation

Geometric transformation techniques are fundamental tools in computer vision that enable a wide range of applications. By applying these techniques, computer vision systems can correct distortions, remove noise, enhance the quality of images and videos, track objects, and overlay virtual objects onto real-world scenes.

Image Alignment

• Image alignment is the process of aligning two or more images that were taken from different positions or angles, in order to create a panoramic image.

• Geometric transformation techniques such as homography estimation and feature matching can be used to align the images.

• This technique is commonly used in photography and video production to create seamless panoramic images and videos.

  

Object Tracking

• Object tracking is the process of tracking the motion of an object in a video over time.

• Geometric transformation techniques such as affine transform can be used to estimate the transformation between frames, allowing the system to track the object's motion.

• Object tracking is used in a variety of applications such as surveillance, robotics, and autonomous vehicles.

  

Augmented Reality

• Augmented reality is a technology that overlays virtual objects onto real-world scenes, creating a mixed reality experience.

• Geometric transformation techniques are used to accurately place the virtual objects in the real-world scene, taking into account the camera's position and orientation.

• This allows the virtual objects to appear as if they are part of the real world.

• Augmented reality is used in a variety of applications such as entertainment, education, and marketing.

  

Algorithms for Geometric Transformation

Algorithms are fundamental tools in computer vision for estimating geometric transformations and identifying corresponding features between different images.

Standard Algorithms

• Scale-Invariant Feature Transform (SIFT):

  SIFT is a feature detection and matching algorithm that is commonly used for image alignment and object recognition. SIFT detects distinctive features in an image, such as corners and edges, and matches them between different images, allowing for the estimation of the transformation between the images.

  Pseudocode for SIFT:

  1. Detect keypoints in the image using the Difference of Gaussians (DoG) pyramid.
  2. Compute gradient magnitudes and orientations for each pixel.
  3. Assign orientation to keypoints based on local gradient directions.
  4. For each keypoint, generate a descriptor by sampling gradient orientations in its neighborhood.
  5. Normalize and threshold the descriptor to ensure invariance to lighting changes and noise.

• Speeded Up Robust Feature (SURF):

  SURF is a feature detection and matching algorithm that is similar to SIFT, but is designed to be faster and more efficient. SURF uses a series of image filters to detect features, and then matches them between images using a similar process to SIFT.

  Pseudocode for SURF:

  1. Construct integral images for the input image and its derivatives.
  2. Identify interest points based on the Hessian matrix response.
  3. Assign orientations to interest points using Haar wavelet responses.
  4. Create SURF descriptors by sampling Haar wavelet responses in the region around each interest point.
  5. Normalize and threshold the descriptors to achieve robustness to changes.

Machine Learning Based Algorithms

Machine learning-based algorithms have been widely used for geometric transformations in computer vision, including:

• Convolutional Neural Networks (CNNs):

  CNNs are a popular type of neural network architecture that can learn to estimate the transformation between two images. By processing the features of the input images and detecting corresponding points, CNNs can learn to estimate the transformation parameters, such as translation, rotation, scaling, and shearing.

• Spatial Transformer Networks (STNs):

  STNs are a type of DNN that can learn to perform geometric transformations on images. STNs consist of a localization network, grid generator, and sampler, which work together to estimate the transformation parameters and apply the transformation to the input image.

  Pseudocode for a CNN with Spatial Transformer Module:

  1. Define the architecture of the CNN, including convolutional and fully connected layers.
  2. Integrate a Spatial Transformer Module (STN) into the network.
  3. The STN includes a localization network (predicts transformation parameters) and a grid generator.
  4. During forward pass, the STN applies the predicted transformation to the input feature map.
  5. Train the network end-to-end, where the loss accounts for both the transformation and main task.

• Generative Adversarial Networks (GANs):

  GANs are a type of neural network architecture that can learn to generate realistic images from noise. By incorporating geometric transformations into the GAN framework, GANs can learn to generate realistic images that are transformed versions of the input images.

  Pseudocode for GAN-based Image-to-Image Translation:

  1. Define a generator network that transforms images from one domain to another.
  2. Define a discriminator network that distinguishes between real and generated images.
  3. Train the generator and discriminator alternately in a GAN framework.
  4. The generator tries to minimize the discriminator's ability to distinguish its generated images.
  5. The discriminator aims to correctly classify real and generated images.

Implementation of Geometric Transformation in Computer Vision

Several popular computer vision libraries provide built-in functions and tools to implement geometric transformations. Here's an overview of how geometric transformations can be implemented in two widely used libraries: OpenCV and TensorFlow.

OpenCV:

• OpenCV offers a comprehensive set of geometric transformation functions, including rotation, translation, scaling, and perspective transformation.
• It's highly efficient due to its C++ implementation and optimized algorithms, making it suitable for real-time applications.
• OpenCV supports various image formats, enabling loading, saving, and manipulation of images in different formats.
• It includes robust feature detection and matching algorithms like SIFT and SURF, aiding in tasks that involve finding corresponding points between images.
• OpenCV can be integrated with other libraries and frameworks like NumPy and Matplotlib, providing a versatile toolkit for computer vision.
• It's widely used for image manipulation, processing, and computer vision tasks.

TensorFlow:

• TensorFlow offers high-level APIs like tf.contrib.image and tf.keras.preprocessing.image for geometric transformations like rotation, translation, scaling, and cropping.
• It supports GPU acceleration, which speeds up geometric transformations, particularly useful for deep learning-based tasks.
• TensorFlow Graphics is an extension library catering to geometric transformations in computer graphics, including mesh and camera projection transformations.
• It seamlessly integrates geometric transformations into neural networks through layers like spatial transformers, enabling end-to-end learning of transformations.
• TensorFlow allows distributed computing, making it suitable for large-scale computer vision projects, and provides tools for model deployment across various platforms.

Here's an example implementation of the four main geometric transformations (translation, rotation, scaling, and shearing) using Python and the OpenCV library:

Step 1. Importing Libraries:

Step 2. Translation Function:

Step 3. Rotation Function:

Step 4. Scaling Function:

Step 5. Shear Function:

Step 6. Example Usage:

Step 7. Display Transformed Images:

Output:

Challenges and Future Directions

Challenges in Geometric transformation in computer vision:

• Computational complexity:

  Geometric transformations can be computationally expensive and time-consuming, especially for large-scale applications.

• Robustness:

  Geometric transformations can be sensitive to noise, outliers, and other sources of error, leading to inaccuracies and decreased performance.

• Generalization:

  Geometric transformations may not generalize well to new or unseen data, requiring additional training or adaptation.

Future directions of Geometric transformation in computer vision:

• Self-supervised learning:

  Training geometric transformation models without explicit supervision can improve their performance and generalization capabilities.

• Deep reinforcement learning:

  Reinforcement learning approaches can be used to learn geometric transformations for specific tasks or environments.

• Integration with other computer vision tasks:

  Geometric transformations can be integrated with other computer vision tasks, such as object detection and segmentation, to improve their accuracy and efficiency.

• Real-time implementation on embedded devices:

  Real-time implementation of geometric transformations on low-power embedded devices can enable applications such as robotics and autonomous vehicles.

• 3D geometric transformation:

  Extending geometric transformations to 3D can enable new applications in fields such as augmented reality, medical imaging, and 3D object recognition.