Graph Coloring Problem | Scalar Topics

Problem Statement

We are given a graph, we need to assign colors to the vertices of the graph. In the graph coloring problem, we have a graph and m colors, we need to find a way to color the vertices of the graph using the m colors such that any two adjacent vertices are not having the same color.

Refer to the example and explanation sections for more details and the approach section to understand the solution to the graph coloring problem.

Note: The graph coloring problem is also known as the vertex coloring problem.

Example

The given (input) graph is :

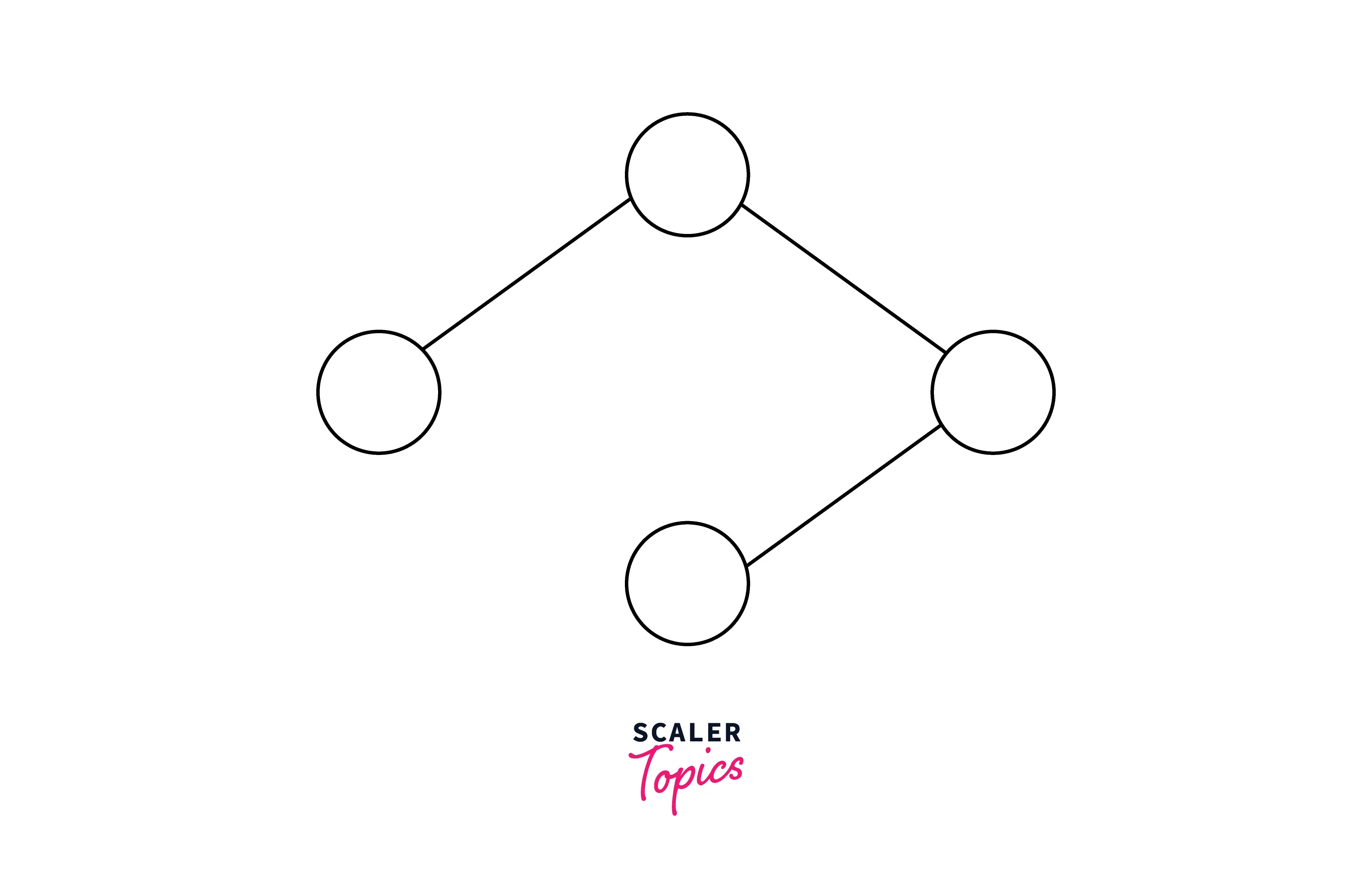
input-graph1

The user needs to color the graph using m colors i.e. in this problem, m is given as 2.

After the graph coloring problem is solved, the colored graph will look like this:

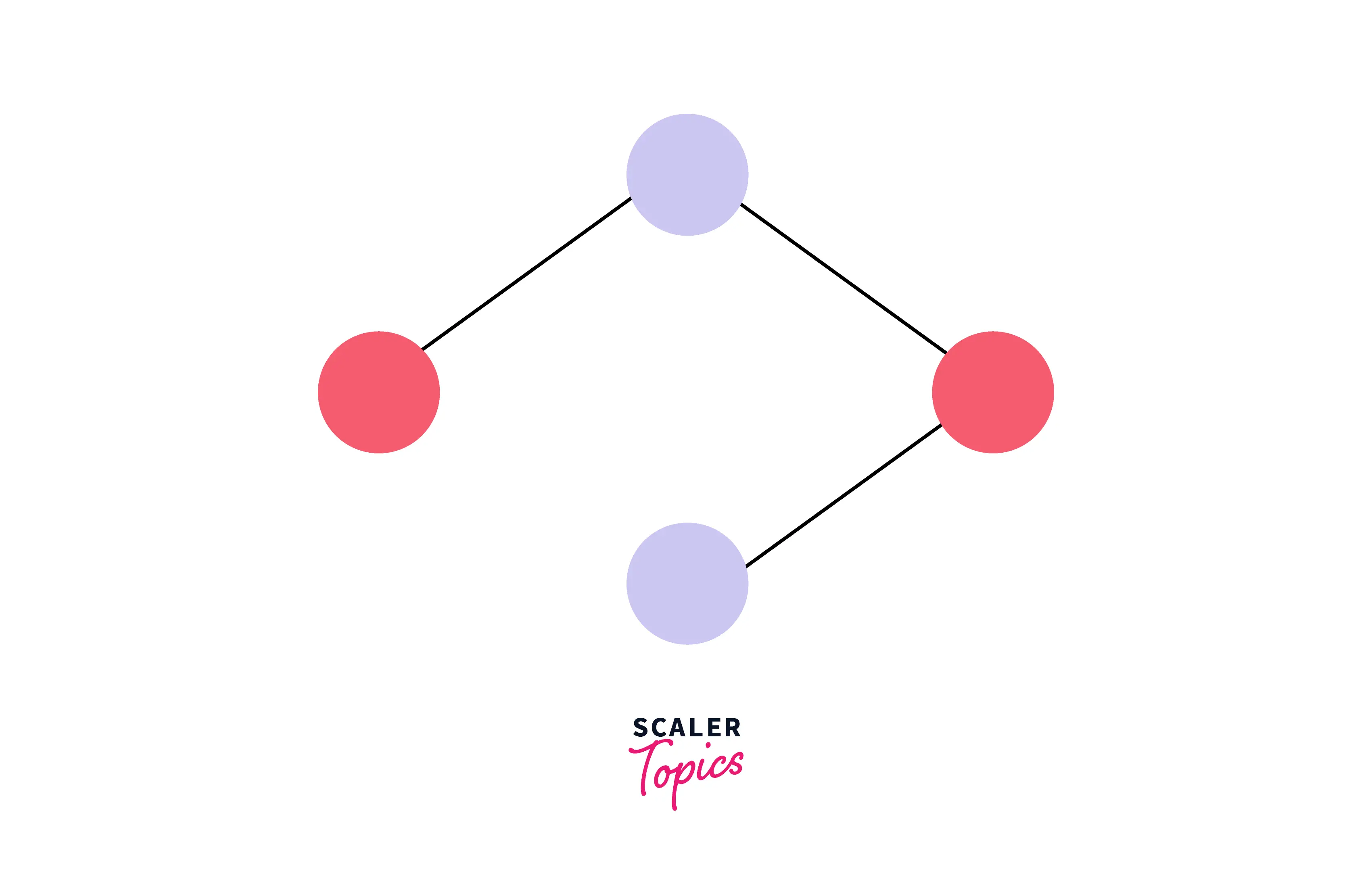
input-graph1-solved

Example Explanation

Before moving into the explanation of the graph coloring problem, let us first understand the term Chromatic Number. The chromatic number is the minimum number of colors needed to color the graph with the constraint that no two adjacent vertices have the same color.

For the explanation of the example, let us first number the vertices.

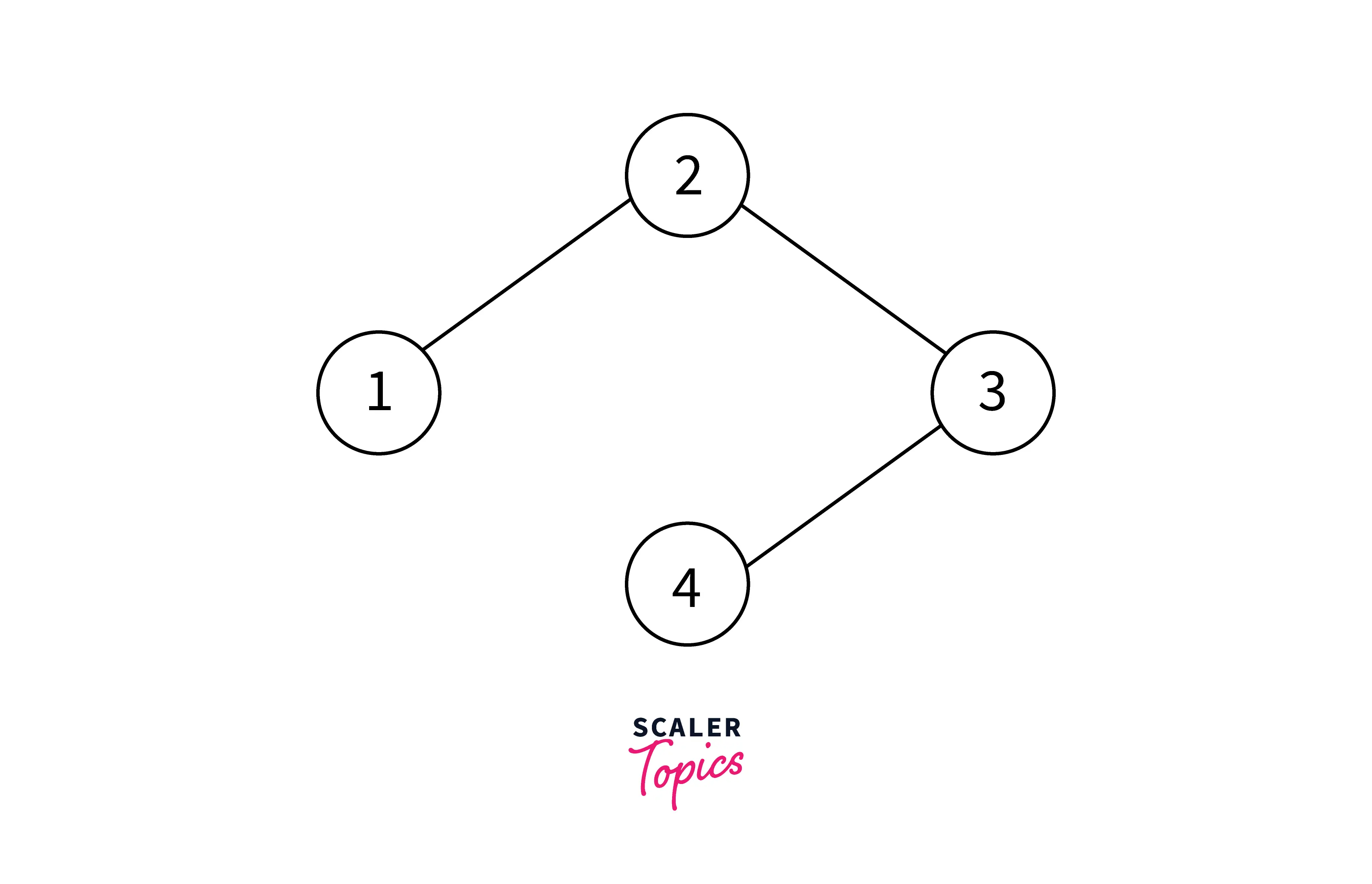
chromatic-number-graph

We have the graph with 4 vertices and the value of m is 2.

Let us suppose that we have started with color-1 (i.e. orange color) and we colored the first vertex with the color-1. Now the connected vertex (vertex-2) must be colored with different colors, so we colored the second vertex with the color-2 (blue).

The current situation after the vertex-1 and vertex-2 are colored is:

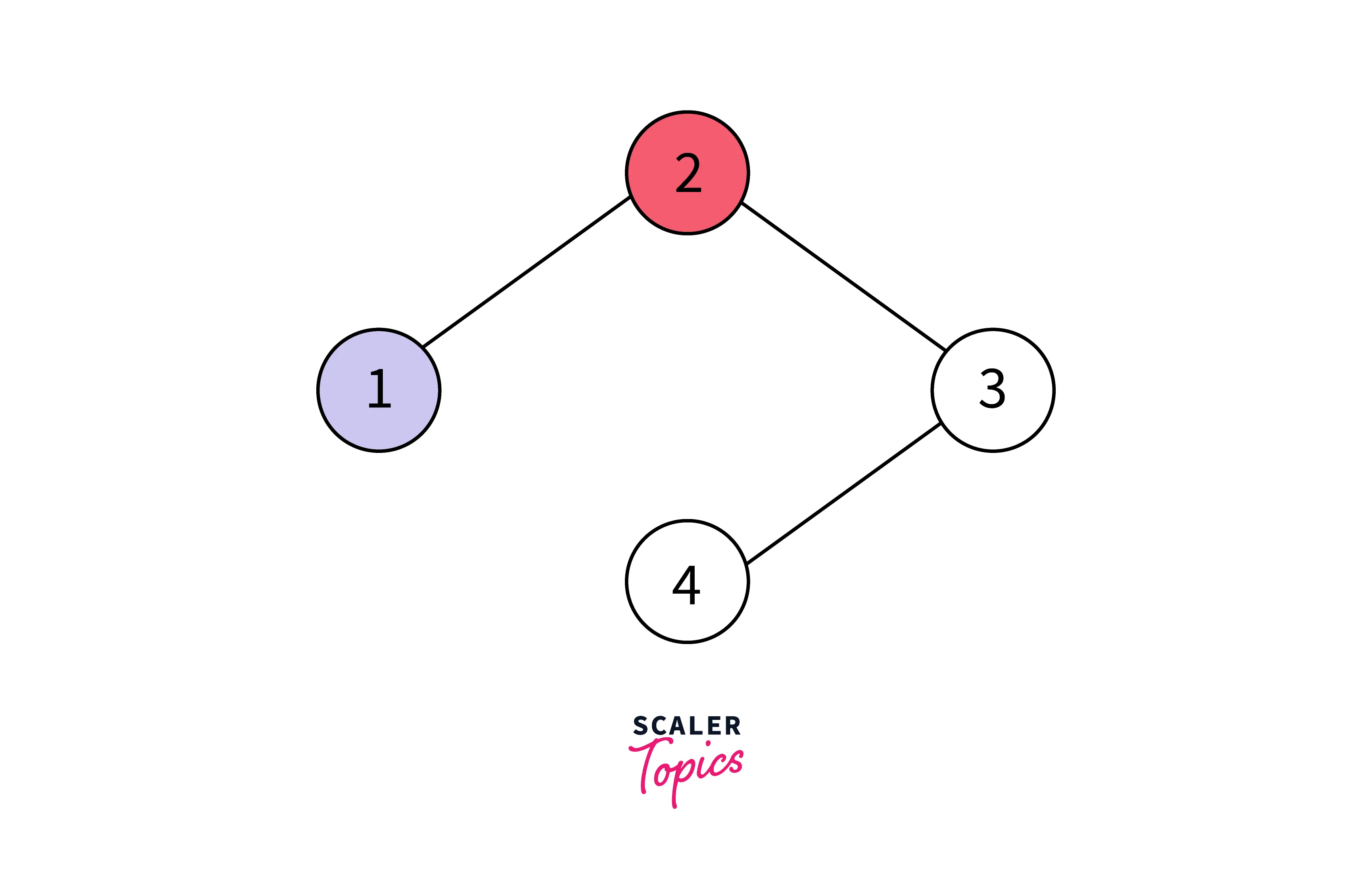
chromatic-number-graph-solved

For the third vertex, we can use another color but the graph coloring problem states that we have to use the minimum number of colors. So. we can color the vertex-3 with the color-1 (orange).

Finally for the last vertex, i.e. vertex-4 we cannot use the color-1, so we colored it with the color-2 (blue).

Hence, all the vertices of the graph coloring problem are colored with only 2 colors (m = 2).

Constraints

The first input is the number of vertices present in the graph i.e. n (1 ≤ n ≤ $10^3$ ).
The second input is the sequential set of vertices of the graph.
The third input is the value of m $(1 <= m <= n)$ i.e. number of colors to be used for the graph coloring problem.

In some problems, you may find the number of test cases represented by t. So, we only need to call the graph coloring problem function t-times.

Approach 1: Brute Force

The brute force approach to solving the graph coloring problem can be generating all the possible color combinations. After the color generation, we can check if any two adjacent vertices are having the same color or not. The time complexity will be huge as we have to generate all the possible combinations.

Note: All the possible combinations can be $m ^ V$ where V is the number of vertices.

Pseudo code can be:

Define a recursive function that takes the current index (i), several vertices, and the color array for output.
Check if the current color is safe i.e. no two adjacent vertices have the same color. Then print the current color configuration and break the loop.
Assign a color to the vertex. The range of assigned colors is from 1 to m.
Now, for every color assigned, call the recursive function.
If the recursive call returns true then the coloring is possible. So, break the loop and return true.

C++ Code:

Java Code:

Python Code:

Output:

Complexity Analysis

In the brute force approach to the graph coloring problem, we are generating total $m^V$ combinations of the color. So, it requires exponential time.

Time Complexity

In the brute force approach to the graph coloring problem, the time complexity is $O(m^V)$ .

Space Complexity

In the brute force approach to the graph coloring problem, we are not using any extra space but we are using the recursive stack for the recursive function call. So, the space complexity is O(V).

Approach 2: Backtracking

The backtracking approach to solving the graph coloring problem can be to assign the colors one after the other to the various vertices. The coloring will start with the first index only but before assigning any color, we would first check if it satisfies the constraint or not (i.e. no two adjacent vertices have the same color). If the current color assignment does not violate the condition then add it into the solution else, backtrack by returning false.

Pseudo code can be:

Define a recursive function that takes the current index (i), several vertices, and the color array for output.
Check if the current color is safe i.e. no two adjacent vertices have the same color. Then print the current color configuration and break the loop.
Assign a color to the vertex. The range of assigned colors is from 1 to m.
Now, for every color assigned, call the recursive function.
If the recursive call returns true then the coloring is possible. So, break the loop and return true. Else, backtrack.

C++ Code:

Java Code:

Python Code:

Output:

Complexity Analysis

In the backtracking approach of the graph coloring problem, we are generating total $m^V$ combinations of the color. So, it also requires exponential time.

Time Complexity

In the backtracking approach of the graph coloring problem, the time complexity is $O(m^V)$ . In the backtracking approach, the average time complexity is less than $O(m^V)$ .

Space Complexity

In the backtracking approach to the graph coloring problem, we are not using any extra space but we are using the recursive stack for the recursive function call. So, the space complexity is O(V).

Note: The backtracking approach and the brute force approach have the same time complexity as in the backtracking algorithm we are just eliminating the bad decisions while coloring the vertices.

Approach 3: Brooks’ Theorem

We can also solve this problem using Brook's Theorem. Brook's theorem tells us about the relationship between the maximum degree of a graph and the chromatic number of the graph.

The statement of Brook's Theorem is:

For a simple connected graph G, which is neither is complete graph nor an odd cycled graph, the relationship between the maximum degree of a graph and the chromatic number of the graph is X(G) ≤ k, where k denotes the maximum degree of the graph G, and X(G) denotes the chromatic number of the same graph G.

Approach 4: Greedy Approach

The greedy approach to solving the graph coloring problem can be using at most x+1 colors if the maximum degree of a vertex is x. The greedy approach does not guarantee that the minimum number of colors are used but, surely, the maximum x+1 colors are used where x is the maximum degree of any vertex in the given graph.

We will color the current vertex with the least-numbered color. After that, we will check if the currently assigned least color has been used previously for any adjacent vertex of the current vertex or not. If it is not used then we can continue the process to the next vertex else, we will assign the next color.

Let us see the pseudo-code for the same.

Pseudo code can be:

Color the first vertex of the graph with the first color.
Repeat the below step for the remaining vertices. Color the current vertex with the minimum numbered color. Make sure that the selected minimum number color has not been used previously for any adjacent vertex of the current vertex.

C++ Code:

Java Code:

Python Code:

Output:

Complexity Analysis

In the greedy approach to the graph coloring problem, we are greedily assigning a color to each vertex of the graph as well as checking if the assigned color meets the criteria or not (no two adjacent vertexes have the same color).

Time Complexity:

In the greedy approach to the graph coloring problem, the time complexity is $O(V^2 + E)$ in the worst case.

Space Complexity

In the greedy approach to the graph coloring problem, we are not using any extra space. So, the space complexity is O(1).

Conclusion

The brute force approach to solving the graph coloring problem can be generating all the possible color combinations and checking if any two adjacent vertices are having the same color or not.
The backtracking approach is also a type of brute force. It is just used to eliminate bad decisions while coloring the vertices.
In the brute force approach to the graph coloring problem, the time complexity is $O(m^V)$ , and space complexity is O(V).
The backtracking approach to solving the graph coloring problem can be to assign the colors one after the other to the various vertices. If the current color assignment does not violate the condition then add it into the solution else, backtrack by returning false.
In the backtracking approach to the graph coloring problem, the time complexity is $O(m^V)$ , and space complexity is O(V).
The greedy approach to solving the graph coloring problem can be used at most x+1 colors if the maximum degree of a vertex is x. The idea is to color the current vertex with the minimum numbered color that has not been used previously for any adjacent vertex of the current vertex.
In the greedy approach to the graph coloring problem, the time complexity is $O(V^2 + E)$ in the worst case, and space complexity is O(1).
We can also solve this problem using Brook's Theorem. Brook's theorem tells us about the relationship between the maximum degree of a graph and the chromatic number of the graph.