Greatest Integer Function

The greatest Integer function, represented by [x], returns the greatest integer value less than or equal to x. Here, x can be a decimal or floating point number or an integer.
Integer data type represents whole numbers without decimal points or fractional parts. These are useful for counting and places where fractional values are irrelevant such as the index of an array. Floating point data types are float and double. These can represent both whole numbers and fractional numbers. These may introduce rounding errors or loss of precision.
The greatest integer function is also called the step function as the graph of the function is a step curve. It rounds the number to return the floor of that number. Most of the programming languages provide a floor function which can be used to calculate the greatest Integer function.
The domain of the greatest integer function is the real numbers (R) and the range is whole numbers (Z).
This function is very often used by programmers when they want to truncate the value to integers so that these can be used for array indices, operations, etc. It also finds its applications in cryptographic applications, signal processing, resource allocation, etc.

Problem Statement
Implement a program or function to calculate the greatest integer function, denoted as [x]. The greatest integer function rounds down a given real number [x] to the largest integer less than or equal to x.
Input:
- A real number x (e.g., a floating-point value).
Output:
- The greatest integer less than or equal to x.
Constraints:
- The input x is a real number within the range of representable values in the chosen programming language.
Note:
- Ensure that your implementation works correctly for positive and negative values, as well as zero.
Examples
Examples:
Note: In the third example the round-off value for a negative number -3.2 has to be less than -3.2 which is -4 instead of -3.
Number Line Representation
Let us understand this with the help of a number line representation. We will see how the values of [x] and x are presented on a number line.
Let us take an example of [x] = [-15.698]. Now from the above definition, we know that the greatest integer for the given x is -16.

Let us take an example of [x] = [48]. The greatest integer equal to or less than the given x is 48.

Let us take an example of [x] = [45.99] = 45.
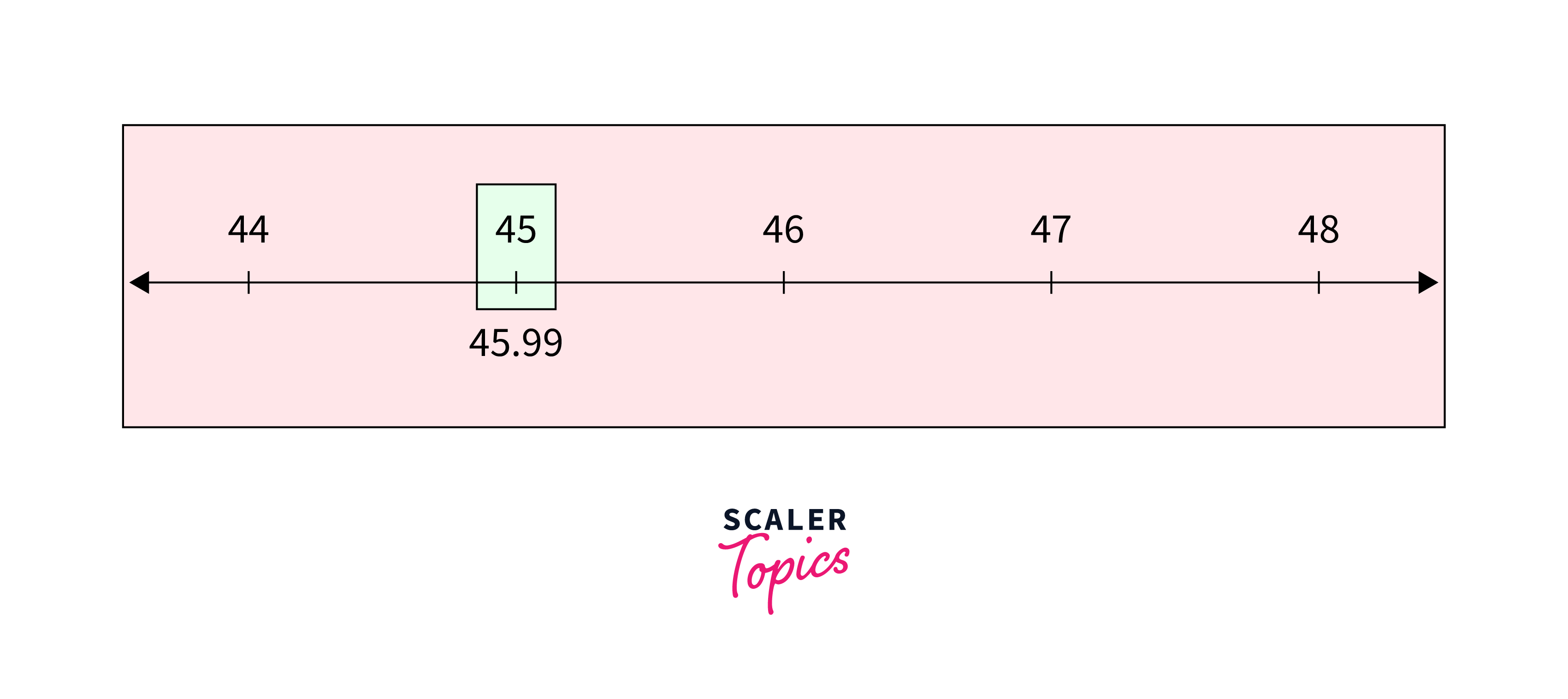
From the above representations we can conclude that if x is an integer, then the greatest integer is equal to the x itself. In case x is a real number then the first integer on the left-hand side is the greatest integer on the number line.
Greatest Integer Function Graph
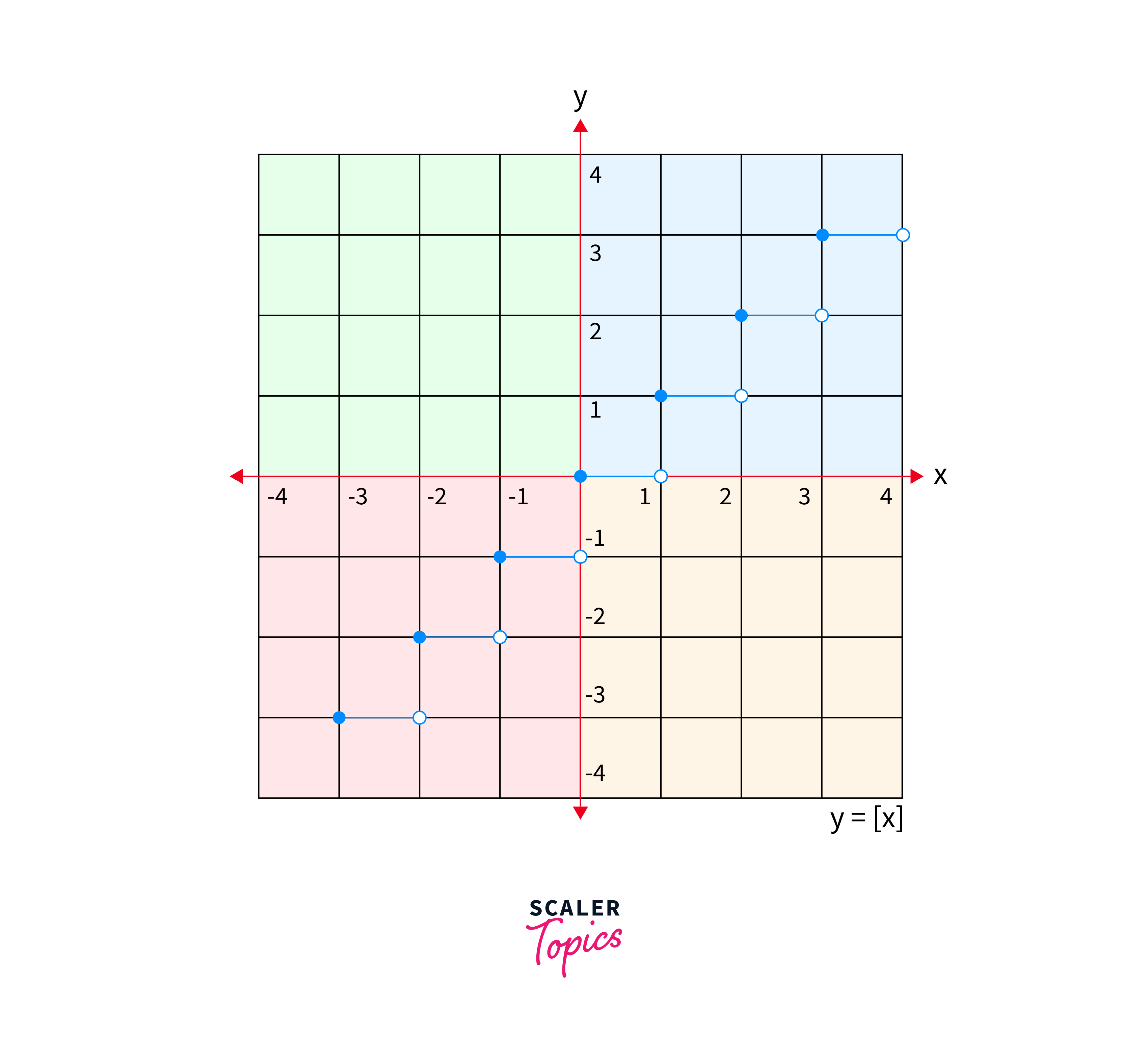
The greatest integer function is a step function and thus its graph is a set of steps. In the above graph, the endpoint on the left of every step is blocked to represent that they are part of the graph (inclusive), and the endpoint on the right side is an open circle (exclusive) to represent the points that are not part of the graph.
From the above graph, we can conclude that the value of f(x) or y stays constant within an interval. The intervals are of the form [n,n+1) where n is an integer. For this interval, the output of the function is equal to n. Here, n is inclusive, and n+1 is exclusive. This behavior is due to the fact that the greatest integer function rounds down to the nearest integer.
For example, let us say the value of x = 3.67. In the graph, there is a blue line on the top right corner of the graph starting from x = 3 inclusive and extending till x = 4 exclusive. For these range values, it indicates that the value of y = 3.
Greatest Integer Function Properties
The properties of the Greatest Integer Function are as follows:
- If x is an integer [x] = x.
- The above is true for negative numbers as well i.e. [-x] = -[x] = x. As x is an integer.
- If x is a real number and less than zero then, [-x] = [-x] - 1.
- [x + N] = [x] + N holds true when N is an integer.
- If [f(X)] >= Y then f(X) >= Y
Program to Implement the Greatest Integer Function
All the programming languages provide a built-in function for getting the greatest integer function.
Inside the greatest_integer() function we are first checking if the input is NaN or positive/negative infinity. In that case, we are throwing an error or exception as it is not possible to find the greatest integer.
The in-built floor() function returns a double value. But our function must return an integer value and therefore, we have implemented a check if the returned value is out of bound for integers. Double can store large values which don't fit it integer due to its smaller size and we may get an undesired result.
In the main or driver method, we are catching the errors and printing the error message to the user.
Python's math module contains the function floor which returns the greatest integer.
In C, the math.h header file provides the floor function for returning the greatest integer function.
The C++ uses the math library from inherited the C called the <cmath> header.
In Java, the Math class gives the floor method. It works similarly as in the case of the programming languages.
Conclusion
- Greatest Integer function is a step function. It returns a floor value i.e. the greatest integer less than the given x.
- All the programming languages provide a built-in function to calculate the floor value for all the floating point values in their Math operations libraries.
- We can use the number line to represent the greatest integer function.
- Graph can also be used to plot the function. Here, the graph is a group of steps. The value is constant for an interval.
To learn more about such interesting and useful topics visit here.
:::
